Расчет геометро-кинематических характеристик зацепления арочных зубьев цилиндрической передачи при погрешностях взаимного расположения

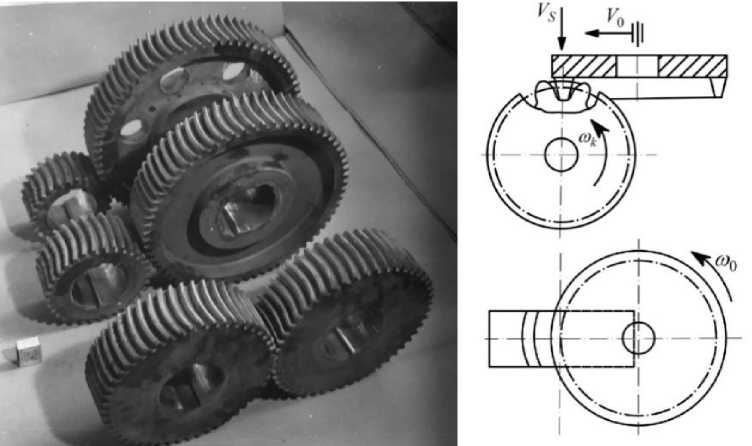
Цилиндрические зубчатые передачи с арочными зубьями, представленные на рис. 1а, при эксплуатации в нежестких корпусах моделей энергонасыщенной техники (например, при эксплуатации передач верхних приводов буровых машин; конечных передач локомотивной техники; передач бортовых редукторов аграрной техники; приводов вертолетов; шестеренчатых насосов) обеспечивают, в отличие от косозубых и прямозубых колес, увеличение надежности и долговечности передач по показателям контактной и изгибной выносливости зубьев [1]. Несмотря на это, в приводах машин они используются крайне редко. Основной причиной этого является отсутствие специализированного зуборезного оборудования для производства цилиндрических колес, которые применяются в арочных цилиндрических зубчатых передачах [1, 2]. К настоящему времени предложено полтора десятка различных приемов и методов проектирования и производства арочных зубьев цилиндрических колес [1–14], отличающихся применяемыми инструментами и формообразующими движениями. Основой многих из разработанных способов являются способы нарезания криволинейных зубьев конических колес [15, 16], хотя известны и оригинальные

[1, 5, 7, 11], применяемые лишь для металлообработки исследуемого типа зубьев. В отличие от иных цилиндрических передач с косыми и прямыми зубьями, различные способы формообразования которых обеспечивают практически одинаковую геометрию поверхностей зубьев, геометрические параметры главных поверхностей арочных зубьев существенно зависят от способа их формообразования и принципиально изменяют геометро-кинематические характеристики зацепления зубьев в передаче. Анализ известных приемов и методов производства исследуемого типа зубьев свидетельствует [1, 2], что наибольшие перспективы промышленной реализации имеет метод получения зубьев, который реализуется резцовыми круговыми головками обкатом с периодическим делением, как показано на рис. 1б. Реализация способа возможна на четырех координатных станках с числовым программным управлением, при этом необходимый зуборезный инструмент широко используется при нарезании круговых зубьев конических колес по схеме Глисон как на отечественных, так и на зарубежных зуборезных станках [1, 2, 6, 10, 11, 13].

а)

б)

Рис. 1. Передачи с арочными зубьями (а) и расчетная схема (б) нарезания зубьев резцовой головкой

Следуя приведенной на рис. 1б схеме, главная поверхность арочного зуба цилиндрического колеса является однопараметрической огибающей семейства производящей поверхности инструмента [1] в относительном движении, при этом геометрические особенности поверхностей зубьев могут быть вскрыты лишь при использовании теории пространственных зацеплений. Однако в большинстве работ [10, 11, 13], посвященных процессу формообразования арочных зубьев колес данным способом, отмеченное обстоятельство не учитывается, поскольку построение моделей выполняется в рамках теории плоских зацеплений. Отсутствуют данные по исследованию геометро-кинематических характеристик зацепления арочных зубьев при работе передачи в условиях различных погрешностей взаимного положения шестерни и колеса, что не позволяет реализовать процесс проектирования цилиндрических передач с арочными зубьями с учетом условий их работы в эксплуатации.

Цель статьи - на основе теории пространственных зацеплений реализовать построение математических моделей формообразования арочных зубьев режущим инструментом (круговая и резцовая головка) методом обката с периодическим делением и исследовать геометрокинематические характеристики их зацепления в условиях ненулевых погрешностей относительного положения колеса и шестерни в передаче.

Математические модели процесса формообразования главных поверхностей арочных зубьев шестерни и колеса

В представленном способе обработке арочных зубьев колеса инструментом является круговая резцовая головка (рис. 1б), которая вращается вокруг собственной оси с необходимой для процесса резания скоростью. В результате процесса резания исследуемого типа зубьев инструмент согласованно с вращением заготовки колеса осуществляет поступательное перемещение в направлении, перпендикулярном оси вращения колеса [1, 2, 9–11]. Деление происходит после обработки впадины зуба колеса. Далее выполняется поворот заготовки колеса на величину оборота, кратного угловому шагу зубьев колеса, инструмент и заготовка колеса возвращаются в исходное положение, и процесс циклически повторяется для нарезания последующих впадин зуба колеса. Описанный процесс формообразования главной поверхности арочного зуба соответствует зацеплению зуба производящей рейки, поверхность которого представляет собой прямой круговой конус, с зубом нарезаемого колеса (шестерни) и реализует метод обката с единичным делением. В данном случае главная поверхность арочного зуба является однопараметрической огибающей семейства поверхностей зубьев производящей рейки [1, 2]. В разрабатываемых далее моделях используем нижний индекс 2 для параметров выпуклой поверхности арочного зуба колеса и нижний индекс 1 для параметров вогнутой поверхности арочного зуба шестерни.

Производящей поверхностью круговой резцовой головки в системе координат Sp ( x_p , Ур , Zp ), жестко с ней связанной, является прямой круговой конус. Необходимая скорость резания в процессе формообразования арочного зуба обеспечивается вращением головки вокруг оси Ур . Поверхность прямого кругового конуса образуется вращением прямолинейной режущей кромки резца, расположенной в плоскости, проходящей через ось Ур резцовой головки, вокруг этой оси. Проекции Xp , Ур , Zp радиус-вектора Tp (jXp , Ур , Zp^ производящей поверхности резцовой головки имеют вид [3]:

Xp =соs^2 (^U2 sin Ct₀ - Г_д2); Ур = соs СГ₀ ; z_p =sin^2 (^U2 sin Ct₀ - Г_д2).              (1)

Здесь обозначено: 1^2 – линейный параметр прямолинейной кромки резцовой головки; ^2 – угол поворота режущей кромки вокруг оси Ур ; СГ₀ – угол наклона режущей кромки относительно оси Ур (угол исходного производящего контура); Гд₂ – расчетный радиус резцовой головки при нарезании колеса.

Проекции ТПр_Х , ТПру , ™pz орта нормали ТПр (т_рх , ТПру , Шр^ поверхности (1) описываются выражениями [3]:

ТПрх =соs «о соs ^2 ; Ш_ру = -sin сг₀ ; TTlpz =соs «о sin ^2 .                                (2)

Чтобы определить главную поверхность выпуклой стороны исследуемого типа зубьев колеса необходимо учитывать тот факт, что она является однопараметрической огибающей семейства производящей поверхности круговой резцовой головки в заданном относительном движении, – при повороте заготовки колеса на угол ^2 режущий инструмент поступательно перемещается в направлении, перпендикулярном оси вращения колеса, на величину ^2 =       =       ∗/2, где ^w2. – радиус начальной окружности обрабатываемого колеса, mn – нормальный модуль, z∗ – число зубьев нарезаемого колеса. Резцовая головка выполнена с внутренними резцами.

С учетом [3, 15–17], главная поверхность выпуклой стороны арочного зуба цилиндрического колеса будет выглядеть как представлено ниже:

^̃ 2(u₂ , ^2 , Ф2 )=^2 , P ( Фг ) ̃_D( u₂ , ^2 ); f2 ( ^2 , ^2 , Ф2 )=0,                                         (3)

где ̃2( ^2 , ^2 , Ф2 ) – матрица-столбец, составленная из проекций координат %2 , У2 , ^2 радиуса вектора r₂ ( %2 , У2 , ^2); _,( Ф2 ) – матрица перехода четвертого порядка, описывающая переход от системы координат Sp ( Xp , Ур , Zp ) к системе координат ^2 ( %2 ,У 2, ^2), жестко связанной с колесом (рис. 2); Ф2 – угол поворота колеса при формообразовании выпуклой поверхности арочного зуба; второе уравнение в выражении (3) является уравнением связи параметров tZ.2 , ^2 и Ф2 , – уравнение станочного зацепления [3, 15, 17].

Элементы матрицы _,( Ф2 ) определим на основе рис. 2 , на котором представлены используемые системы координат и переходы .

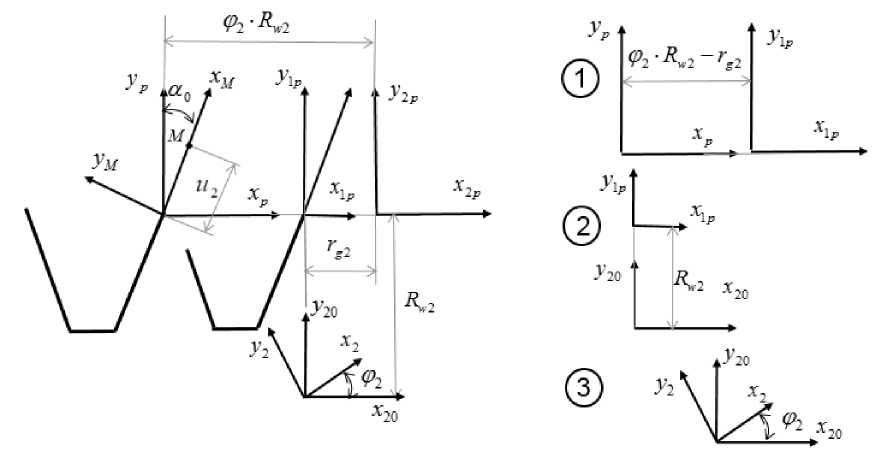
Рис. 2. Системы координат и переходы для определения элементов матрицы ^А2,_р (ф г )

Матрица А ₂ , _p( ф ₂) имеет вид:

	С05ф2	5Шф2	0
А 2 ,p((P 2 ) —	- 0	С05ф2 0	0 1
	0	0	0

-00sp^ф 2 R_w2 - д_д 2 ) + R_w2s ppp 2 +s i pp с ( ф 2 R_W 2 - Тд 2 ) + R2С0 о Sф 2

0

1

Раскрывая матричное уравнение (3) на основе (4) и (1), найдем выражения для проекций х₂ , у₂, z₂ радиуса вектора r₂(x₂ , У с , Z c ):

х₂ — А с00 sф 2 + B₂simp 2 ;  У с = -А 2 s mp 2 + ВсОоPф 2 ; Z 2 = sipBc^sipa o - д_д 2 )-      (5)

Здесь обозначено:

А с = со sB с (« с s ina₀ - д_д с ) - p 2 R_w2 + т_д2 ;   В— — u₂o os a o + R _w2.

Определим зависимости для расчета проекций координат m_2х , т_{2 у},т_2z орта нормали m₂(т_2х, т_{2 у},т _2z ) главной поверхности выпуклой стороны арочного зуба цилиндрического колеса (3). Воспользуемся выражением:

т2 (Вс,Ф с) = Ас ,p(P с )тр(Вс ), раскрывая которое, установим:

т2х — соФф2cosaocosi92 - sipp2sipao; т2у — -sipp2 cosaocosi9c - cosp2sipao;

m2 z = 0 0 s ao s ipB 2. (7)

Воспользовавшись результатами работ [3, 17], представим уравнение станочного зацепления в виде равного нулю скалярного произведения вектора т_р (т_рх, т_ру,т_{р z}) и вектора Ур₂ (^₂ х , ^_2у, ^₂ z ) — вектора-аналога относительной скорости:

/ с ⁽ U c , B 2 , p с ) = тс^ с = т с ^ _х + т с у ^ у + т с z ^ cz = 0- (8) Расчет проекций У_{2 х},У_{2 у}, У_сz в системе координат S_p(x_p,y_p,z_p) выполняется на основе матричного выражения [3]:

V

2

(« с ,B c ,P c ) =АС,Р(ф2 )^p^gp(u2 ,B c ), (9) где Vq, ₂(u₂,i9 ₂ , p₂ ) - матрица-столбец, составленная из проекций У_{2 ж}, У_су, У_{2 z} радиуса вектора Р ^ ₂ на координатные оси системы S_p(x_p,y_p,z_p); А 2, ((ф _с) - матрица, обратная матрице А _с , _р(p₂ )-

	С05ф2	- 5Шф2	0	^2Rw2 - rg2
(^2)=	5Шф2	С05ф2	0	- ^w2
, ,	0	0	1	0
	0	0	0	1

После дифференцирования элементов матрицы , (ф2 ) (4) по параметру ф2, учитывая (10), (5)

и, раскрывая (9), определим:

^2х =        ^; ^2у =- cos-9₂ (u₂sina₀^- ^₂) + ^2^w2 ^- r_g2 ^;^2z =0.

Искомое уравнение станочного зацепления получим, подставляя выражения (11) и зависимости для проекций Шр_Ж, Шру , TTLp_z (2) в формулу (8):

/2 (u₂ , ^2 , ф₂)= COS0₂ (^u2 - r_g2sma^ - (p₂R_W2sina₀ + r_g2sina₀ =0.                  (12)

Таким образом, для описания выпуклой поверхности арочного зуба колеса, учитывая связь (12), для расчета координат точек получены формулы (5) и формулы (7) для расчета проекций орта нормали в этих точках, определяемых значениями параметров 1Z2 , ^2 и Ф2 .

Способ формообразования главной поверхности вогнутой стороны зуба шестерни по движениям инструмента относительно заготовки аналогичен выше рассмотренному процессу нарезания выпуклой стороны арочного зуба с учетом того, что используемая резцовая готовки имеет наружные резцы. Для определения зависимостей по расчету проекций X^ , У1 , Z^ радиуса вектора f[ (x^, У1 , Zi ) и проекций m_lx , m_ly , m_lz орта нормали mi(m_u , m_ly , m_lz) арочного зуба шестерни в системе координат S^ (x^, У1 , Z^), жестко с ней связанной, в формулах (5), (7) и (12) необходимо заменить нижний индекс «2» на индекс «1» и параметры: Ф2 =- Фз_ ; ^2 =  ; ^2 w=-^1 w ;

^2 = ; Гу2 = . В результате для X^ , У1 , Zi получим выражения:

%1 =         - B^sirup^ ; У1 =         + В^созф^ ; z₂ =      ( UySItUXo - r_gl ).

fl- ( И-у , i9i , Ф1 )= COS0Y (iq - T-gYSi-TUXo) - VYR_WYsina₀ + r_gYsina₀ =0,                     (13)

где ^1 =              - r_sl) - ViRwi + TgY ; B^ =        - Rwi .

Проекции TH-yx , т_1у , т₁₂ рассчитываются по формулам:

m-Yx =                + 51пф₁51па₀ ;    ^mYy =                - со5ф₁зига₀ ;

TTIyz =              .                                                                                      (14)

Определим уравнения сечения арочного зуба шестерни и колеса торцовой плоскостью, проходящей через середину зуба, задание которой соответствует условию Zi = =0. Для выполнения этого условия, на основании (5) для зуба колеса и (13) для зуба шестерни, необходимо положить i9i = =0, при этом уравнения станочных зацеплений (12) и (13) упрощаются:

Uy =             ; u₂ =              .                                                     (15)

Подставляя эти зависимости в формулы для координат X^ , У1 (13) и X2 , У2 (5), определим:

%1 =    [ siTKp-y - Ф₁соза₀ соs ( (Zq - Ф1 )]; У1 =- ^wl [ С05ф-у - Ф₁соза₀ sin ( (Zq - Ф1 )];

^2 =     [ siTKp^ - Ф₂соза₀ соs ((Z_o + Ф2 )]; У2 =     [ C0S(P2 + Ф₂соза₀ sin ((Z_o + ^2)].

Данные выражения являются уравнениями эвольвенты, впервые полученными Н.И. Колчиным. То есть в рассматриваемом способе формообразования профиль среднего сечения поверхности арочного зуба является эвольвентным. Известны [9, 11] модификации этого способа формообразования, при реализация которых в каждом торцовом сечении арочного зуба его профиль представляет собой эвольвенту.

Исследование влияния погрешностей монтажа колеса и шестерни на положение рабочих линий в зацеплении арочных зубьев цилиндрической передачи

Для исследования геометро-кинематических характеристик зацепления арочных зубьев колеса и шестерни необходимо определить координаты точек касания главных поверхностей арочных зубьев. В теории пространственных передач зацеплением [3, 15–17] процедура определения точек касания поверхностей зубьев называется обратной задачей теории зацепления [3, 17]. Решение обратной задачи позволяет определить функцию положения колеса и шестерни в передаче, оценить чувствительность исследуемой цилиндрической передачи с арочными зубьями к погрешностям взаимного положения шестерни и колеса с целью научного обоснования допусков на величины погрешностей. Основой решения обратной задачи являются выражения проекций координат радиусов-векторов и ортов нормалей главных поверхностей арочных зубьев шестерни (13), (14) и колеса (5), (7) и (12), записанных, соответственно, в системах S1(х1,у1,z1) и S2 (х2 ,У2 ,Z2).

Подвижные звенья передачи вращаются вокруг осей z^ (шестерня) и z₂ (колесо), с которыми жестко связаны системы координат S₁(х₁,у₂, z₂ ) и S₂ (х₂, у₂ , z₂). Примем, что началу отсчета угла поворота ip_к-го подвижного звена ( к = 1 - шестерня, к = 2 - колесо) в зацеплении арочных зубьев колеса и шестерни соответствует положение осиу_к (к = 1,2) в осевой плоскости передачи. В общем случае, взаимное положение шестерни и колеса в передаче (при отсутствии вращения) характеризуется межосевым расстоянием , которое отличается от станочного ( ) на величину Д_а, углом перекоса зубьев y, углом непараллельности т] и величиной смещения Д_s средней плоскости зуба колеса относительно этой же плоскости на зубе шестерни.

Для построения математической модели зацепления выпуклой стороны арочного зуба колеса и вогнутой стороны арочного зуба шестерни исследуемой цилиндрической передачи, определим положение системы координат ( , , ) относительно системы ( , , ) (рис. 3) с помощью матрицы перехода четвертого порядка ) , ₂(p ₂,p₂ ) = 11 d ^ 11 ,i,j = 1,4.

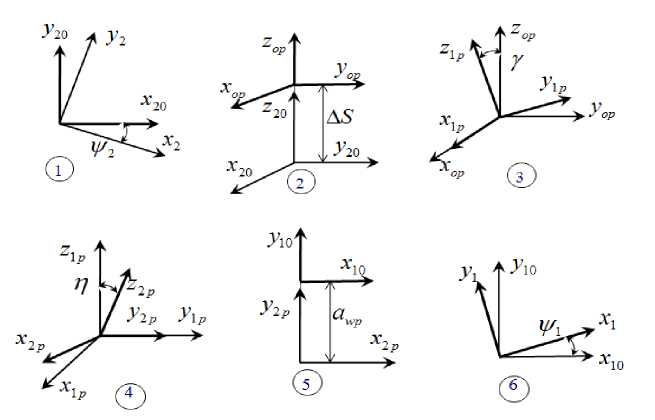
Рис. 3. Системы координат для определения элементов матрицы     (  ,   )

Воспользовавшись построениями рис. 3 для элементов этой матрицы, получим следующие зависимости:

d ₂₂ = 2₂ 1CPPIp₂ + с₂₂ s inp ₂; d ₂₂ = —с_{2 2} s inp ₂ + 1_{2 2} с о sp ₂; d_{2 3} = —s 1пф ₂s iny + со sip ₂s игт) rosy; d _{2 2} = с_{2 2}cosp ₂ + с_{2 2} s inp ₂;d_{2 2} = —с_{2 2} s inp ₂ + с_{2 2}с о sip ₂; d _{2 3} = со sip ₂s iny + s inip ₂s inT cosy; d _{3 2} = —sinT oopip ₂ — со st siny sinp ₂; d _{3 2} = sinT sinp ₂ — со st siny oopip ₂; d _{3 3} = со st rosy; d 24 = ^ wp sinp 2 — Д₅ • с 23 ; d 24 = —n_W pro sp 2 — Д₅ • с 23 ; d з4 = —Д₅ • rosT • соsy;

d 42 = d 42 = d 43 = 0; d 44 = 1,                                                                 (16)

где =          ;    = —          —               ;    = —          +               ;

с₂₂ = sinp₂со st; с₂₂ = соsp₂rosy — sinp₂sinT siny;   с₂₃ = rosp₂siny + sinp₂sinT соsy.

Для расчета проекций координат точки контакта на активной поверхности арочного зуба шестерни, в соответствие с теорией пространственных передач зацеплением [3, 17], фиксируется величина угла поворота шестерни (   =     ) в рабочем зацеплении и решается обратная зада ча зацепления [3, 17]. Следуя работам [3, 15, 16], математическое описание обратной задачи представляет собой систему уравнений, включающую в единой системе координат равенство векторов (  ,   ,   ),   (  ,   ,   ), ортов нормалей (  ,   ),    (  ,   ), а также уравнения связи параметров - уравнения станочных зацеплений (  ,  ,  ) = 0 и (  ,  ,  ) = 0. Про- екции координат точки касания будем определять в системе координат (  ,  ,  ). В этом слу чае система уравнений для решения обратной задачи имеет вид:

̃ (    ,    ,     )=     , (    ,     ) ̃ (    ,     ,)

(   ,    )=    , ( ,    )    (   ,    );(17)

(  ,  ,   )=0;    (  ,  ,)=0

В системе уравнений (17) верхний индекс у матриц определяет систему координат (  ,  ,  ) или (  ,  ,  ), в которой вычислены проекции векторов; ̃ ,     – матрицы- столбцы, составленные из проекций координат радиуса-вектора ̅ (5) и орта нормали (7) выпуклой поверхности зуба колеса в системе координат (  ,  ,  ); ̃ ,    – матрицы-столбцы, составленные из проекций координат радиуса-вектора ̅ (13) и орта нормали (14) вогнутой поверхности зуба шестерни в системе координат (  ,  ,  );  (  ,  ,  )=0 – уравнение зацепления при обработке активной поверхности зубьев шестерни (13);  (  ,  ,  )=0 – уравне ние зацепления при обработке активной поверхности зубьев колеса (12).

Система (17) соответствует условиям касания зуба колеса и зуба шестерни и представляет собой систему семи скалярных трансцендентных уравнений (равенство ортов нормалей дает не три, а два независимых уравнения) с восемью неизвестными:   ,  ,  ,  ,  ,   ,   ,   . Расчет в передаче координат (  ,  ,   ),   (  ,  ,   ) и (  ,  ) точки касания выпуклой стороны арочного зуба колеса с вогнутой стороной арочного зуба шестерни при заданных погрешностях взаимного положения (∆ ,  ,  , ∆ ) шестерни и колеса выполняется по разработанной в среде

MathCad программе при зафиксированной фазе зацепления (   =     ) при варьировании этой фазы в пределах углового шага зуба шестерни путем решения численным методом системы семи трансцендентных уравнений (17) относительно неизвестных ,  ,  ,  ,  ,   ,   .

Результаты анализа влияния погрешностей взаимного расположения шестерни и колеса в передаче на положение рабочих линий в зацеплении арочных зубьев рассмотрим на примере исследования цилиндрической передачи, имеющей следующие параметры: ∗ =23; ∗ =73; модуль нормальный =10 мм; коэффициенты смещения при нарезании зубьев шестерни = 0,44 и зубьев колеса = 0,042; ширина зуба =120 мм; =20 ; радиус начальной окружности шестерни    = 116,115 мм, колеса    = 368,540 мм, межосевое расстояние = 484,655 мм.

Расчеты выполнены для двух вариантов локализации контакта в продольном направлении арочных зубьев. В варианте № 1 (высокая локализация) для нарезания вогнутой стороны арочных зубьев шестерни и выпуклой стороны арочных зубьев колеса используются круговые резцовые головки с расчетными радиусами, соответственно, =220 мм и =215 мм. В варианте № 2 (контакт, близкий к линейному) =220 мм и =218 мм.

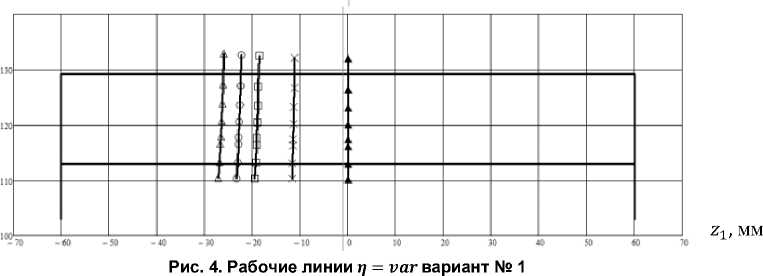
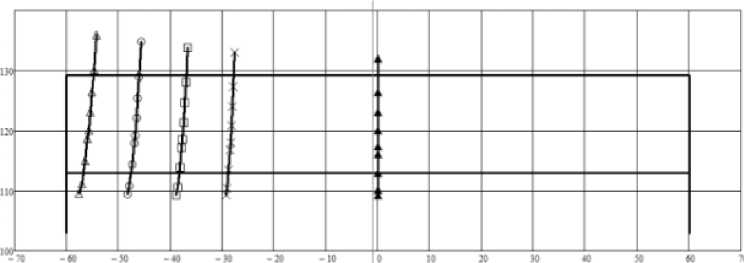
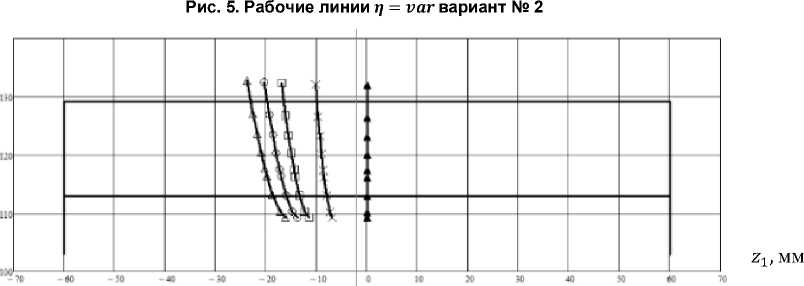
На рис. 4 показаны активные действующие линии (рабочие линии в зацеплении) на поверхности зуба шестерни исследуемой передачи (вариант № 1) при непараллельности ( =   ) осей шестерни и колеса г] = 0' (▲); 3'(х); 5' (□); 6' (о) и 7'(А). Рис. 5 иллюстрирует положение активных действующих линий на поверхности зуба шестерни передачи (вариант № 2) при непарал-лельности (г = vаг) осей шестерни и колеса ц = 0' (▲); 3' (х); 4' (□); 5' (о) и 6' (А).

=   +    =   +

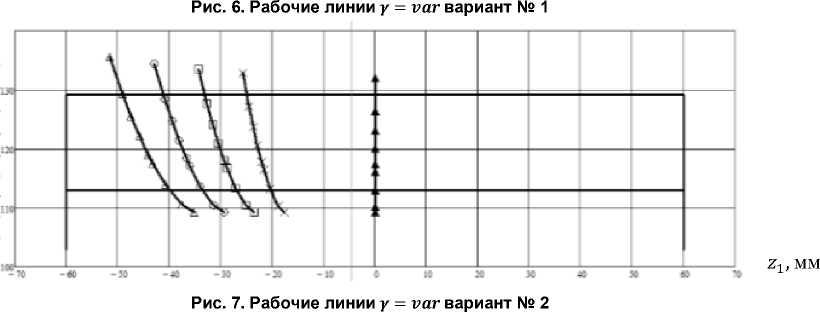
На рис. 6 показаны активные действующие линии (рабочие линии в зацеплении) на поверхности зуба шестерни исследуемой передачи (вариант № 1) при перекосе ( = ) осей шестерни и колеса у = 0' (▲); 3' (х); 5' (□); 6' (о) и 7' (А). Рис. 7 иллюстрирует положение активных дейст- вующих линий на поверхности зуба шестерни передачи (вариант № 2) при перекосе (у = vаг) осей шестерни и колеса у = 0' (▲); 3' (х); 4' (□); 5' (о) и 6' (А).

Pi = , / %i + У1 Pi = / *1 + У1

На рис. 8 показаны активные действующие линии (рабочие линии в зацеплении) на поверхности зуба шестерни исследуемой передачи (вариант № 1) при смещении (Д₅= ^vаг) осей шестерни и колеса Д₅ = 0( ж ); -0,1( х ); -0,5(d); -0,7(о) и -1,0(А) мм. Рис. 9 иллюстрирует положение активных действующих линий на поверхности зуба шестерни передачи (вариант № 2) при смещении (Д₅= vаг) осей шестерни и колеса Д₅= 0( ^ ); -0,1 ( х ); -0,2 (□); -0,3 (о) и -0,4 (А) мм.

P i = ^J * i + у! Pi = Jx+^

Из анализа рис. 4-9 следует, что при отсутствии погрешностей (т = у = Д₅ = 0) рабочая линия располагается в среднем торцовом сечении арочного зуба, в котором его профиль как на шестерне, так и на колесе описывается эвольвентой. Передача является сопряженной, то есть функция положения V₁ = V^CV i ) является величиной постоянной и представляет собой передаточное отношение:

i = — = — = со nst. (18) ?

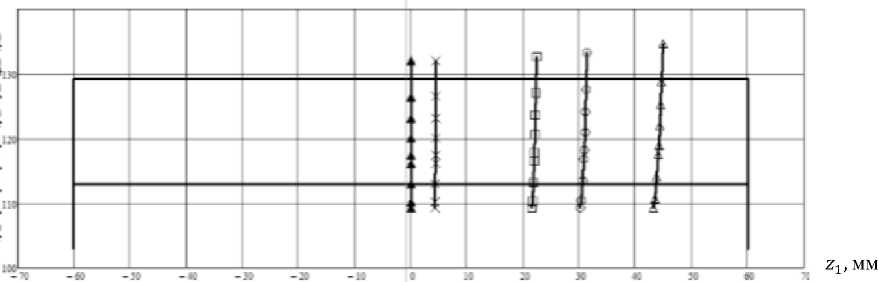
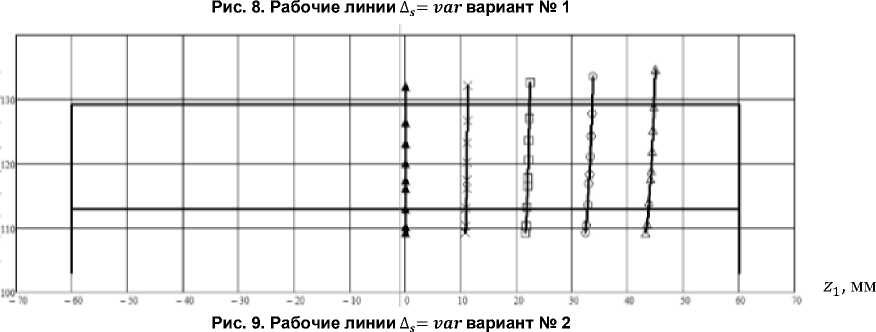
Наличие погрешностей взаимного расположения шестерни и колеса в передаче вызывают смещение рабочих линий из среднего сечения арочного зуба, и функция положения перестает быть постоянной, передача становится несопряженной, возникает циклическая погрешность зацепления арочных зубьев. Известно, что точки рабочей линии являются центром мгновенной площадки контакта, размеры которой зависят от плотности прилегания поверхностей зубьев в окрестности точки их касания. Рис. 4–9 показывают, что более плотный контакт зубьев (передача варианта № 2) обеспечивает снижение контактной нагрузки в зацеплении, однако при наличии погрешностей приводит к значительному смещению рабочих линий из среднего сечения зуба и выходу площадок контакта на торец зубьев. Более того, как будет показано далее, несопряжен-ность передачи существенно возрастает.

Анализ погрешности передаточной функции цилиндрической передачи с арочными зубьями при наличии погрешностей монтажа колеса и шестерни

Работа передачи в условиях погрешностей монтажа шестерни и колеса приводит не только к смещению рабочих линий из средних сечений арочных зубьев, в которых их профиль описывается эвольвентой, но и к нарушению сопряженности передачи, оцениваемой величиной погрешности поворота ведомого звена (Д^₂ ) в период зацепления каждой пары зубьев. Для определения величины Д^₂ для заданной ^ 2 = const фазы зацепления зубьев ведущего колеса (шестерни) решим при ф 2 = с о nst обратную задачу (17) и установим значение ф 2 . После чего погрешность Д^₂ поворота ведомого звена (колеса) передачи рассчитывается по зависимости [15, 18, 19]:

Д^=^ 2 -^ 2^2Л2 /. (19)

Повторяя описанную процедуру при варьировании величины ф± в пределах углового шага зуба шестерни, определим функцию Д^2 = А^2(^i ), характеризующую несопряженность зацепления, – отклонение мгновенного передаточного отношения от постоянного значения (18). Графическое представление зависимости Д = А ( ) для последовательно контактирующих пар зубьев (рис. 10) носит название «кривая Бакстера» [15, 16, 18–20], которая позволяет определить точки геометрического пересопряжения зубьев и оценить кинематическую погрешность зацепления исследуемой передачи. Выполненный в работах [15, 19–21] анализ поведения функции Д^2 = А^2(V^i) свидетельствует, что для правильной работы передачи в реальных условиях экс- плуатации погрешность поворота колеса Дф 2 = Афг^Фi) должна описываться зависимостью, близкой к параболе, в точке экстремума которой, соответствующей центру пятна контакта, Дф2 = 0, а углы ф 1 = 0 и ф( = 0.

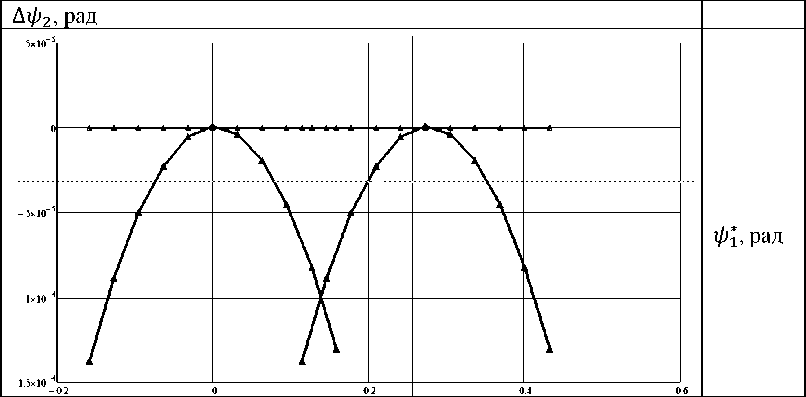
Рис. 10. Кривая Бакстера для приближенных передач зацеплением

В зависимости от геометрии поверхностей зубьев и погрешностей взаимного положения шестерни и колеса в передаче поведение функции Дф2 = Дф2(ф1) может принципиально отличаться от требуемого (рис. 10), обеспечивающего при передаче нагрузки вследствие контактных и изгибных деформаций зубьев уменьшение величины Дф2 при вариации ф1 [15, 16], - реализацию приближенного характера зацепления зубьев.

На рис. 11 представлены результаты расчета функции ∆ =∆ ( ) для двух пар зубьев цилиндрической передачи с арочными зубьями, результаты исследования зацепления которой представлены на рис. 4, 6 и 8 (вариант № 1). Проанализирована кинематика передачи при угле перекоса у = 5 ‘ . Для того чтобы центр пятна контакта (при ф 1 = 0) располагался в районе сечения зуба делительным цилиндром, а не вне активной поверхности арочного зуба, потребовалась коррекция угла а₀ = 20⁰ конической производящей поверхности резцовой головки на величину Дст₀ = 34 ‘ . Фаза зацепления ф 1 =-0,0635 соответствует началу однопарного зацепления (Дф 1 = -1,417 • 10^_4), а ф 1 = 0,0635 (Дф 1 = 3,217 • 10^_4) - выходу из однопарного зацепления арочных зубьев. На рис. 11 точки входа и выхода арочных зубьев в зону однопарного зацепления соединены пунктирной линией.

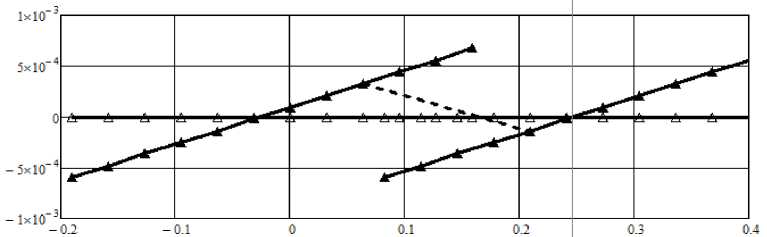
Рис. 11. Функция ∆ = ( ) для цилиндрической передачи с арочными зубьями при наличии угла перекоса зубьев = 5 ′

Из рис. 11 следует, что функция Дф2 = Аф2 (ф 1) имеет пилообразную форму, которая соответствует высокой степени несопряженности передачи, в следствие чего вход зубьев в зацеплении будет происходить с ударом. Выполненные подобные расчеты для передачи варианта 2 показали двукратное увеличение значений ∆ , что является следствием большего смещения рабочей линии от среднего сечения арочного зуба (рис. 4 и 5). Результаты расчета функции Дф2 = А ( ) при ненулевых погрешностях Д и свидетельствуют, что ее характер изменения, по сравнению с функцией, показанной на рис. 11, не меняется.

Аналогичная ситуация имеет место при работе конических передач с круговыми зубьями, что потребовало в рамках теории пространственных зацеплений создания специальных методов локального и нелокального синтеза [15–17] передач с целью исключения ударов при пересопря-жении зубьев и реализации приближенного характера зацепления зубьев. К настоящему времени для конических передач разработаны два [15–17] принципиально различных способа трансформации пилообразной функции Дф ₂ = ^ФгФФ ₁) к виду, показанному на рис. 10. Первый способ предполагает использование в процессе формообразования инструментов (круговых резцовых головок, шлифовальных кругов) с более сложной, нежели прямой круговой конус, производящей поверхностью, изменение геометрических параметров которой позволяет осуществить модификацию профиля кругового зуба. Во втором способе применяются традиционные резцовые головки, а требуемый профиль зуба нарезаемого колеса формируется в процессе обкатки заготовки и производящего колеса на зуборезных станках, имеющих специальное устройство – модификатор обкатки.

Выполненные в настоящей работе исследования цилиндрических передач, арочные зубья которых нарезаются методом единичного деления круговыми резцовыми головками, показали, что получаемая геометрия поверхностей арочных зубьев обеспечивает необходимые геометрокинематические характеристики передач лишь для условий нулевых погрешностей положения шестерни и колеса. Для достижения этих характеристик передач в условиях ненулевых погрешностей ту у и Д₅, требуется в рамках способа формообразования целенаправленная модификация поверхностей арочных зубьев, зависящая как от величины этих погрешностей, так и от закона их изменения в процессе работы передачи. Используя опыт технологической отработки конических передач, процедуры модификации поверхности арочного зуба могут разрабатываться на основе реализации переменного движения обкатки на станках с числовым программным управлением или с использованием резцовых головок, параметры которых, как и закон движения, определяются индивидуально для каждой передачи в результате решения задачи синтеза зацепления, учитывающей особенности процесса формообразования поверхностей арочных зубьев и пространственный характер их зацепления. То есть декларируемая [11, 13] простота и эффективность способа нарезания арочных зубьев резцовыми головками, в том числе с нулевым углом профиля [11], не позволяет обеспечить необходимые геометрические характеристики поверхностей арочных зубьев колес передач, эксплуатация которых осуществляется в условиях ненулевых погрешностей положения колес. Для технологической отработки требуется индивидуальная настройка геометрии поверхностей зубьев на основе специализированного программного обеспечения.

Выводы

• 1.    Для реализации способа формообразования методом единичного деления арочных зубьев цилиндрических колес круговыми резцовыми головками построены математические модели, которые описывают главные поверхности зубьев. Получены зависимости для исследования геометрических характеристик зацепления арочных зубьев, которые учитывают наличие погрешностей положения шестерни и колеса в передаче.

• 2.    В результате исследования геометрии зацепления передачи с арочными зубьями впервые оценено влияние погрешностей положения на смещение рабочих линий в зацеплении зубьев.

• 3.    Впервые для количественной оценки несопряженности исследуемой передачи при ее работе в условиях ненулевых погрешностей положения колес получены данные о погрешности функции положения. Предложены пути обеспечения в рамках рассматриваемого способа формообразования арочных зубьев приближенного характера зацепления зубьев в передаче.