Расчет градиентного оптического элемента, выполняющего заданное преобразование светового поля

Впервые обратная задача в геометрической оптике неоднородных сред была поставлена и частично решена в [1,2]. В [1] найдено аналитическое решение для двумерного волновода, периодически фокусирующего лучи, исходящие из осевой точки. В [2] по заданному двумерному семейству лучей в ГОЭ, построено общее решение для показателя преломления, зависящее от некоторой произвольной функции. Однако это решение не конструктивно и его трудно использовать.

В данной работе предложен метод расчета в лучевом приближении показателя преломления двумерного ГОЭ, переводящего заданное амплитудно-фазовое распределение на входе в заданное амплитудно-фазовое распределение на выходе

Т.е. функцию x = x ( z ) можно обратить, так,

d x что:

d z

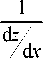
и

_d2 _x d z ²

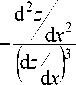
С учетом этого вместо (4) получим:

d2 z
dln n	d x 2
d x     d z d x	1 +f d z _ ^ d x J _

Интегрируя (5) по x , получим:

n ( x ) = C

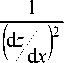
+1

2. Аналитическое решение

Запишем уравнение луча [3] в среде с показателем преломления n :

Подставляя семейство лучей имеющих заданные величины dxdz на прямой z = z ₀ из (6), можно

d Гdr )

—I — n l = v n .

dS ( dS J

Полагая x = x ( z ), y = y ( z ), d S = д/d x ² + d y ² + d z²

–

малое расстояние вдоль луча, получим следующую систему уравнений:

dx dn dn ) f dx ) 2 f 4y --- 1 + --- l + dz dz dx J [ . dz J < dz dy dn dn ) f dx f fjy ---- ^^^^— --- 1 + l + dz dz dy J < dz J < dz d2x

+ n-:- = 0 d z ²

_d2 _y

+ n—v = 0 d z ²

,

Предполагая среду бесконечно протяженной вдоль оси y т.е. n = n ( x , z ), приходим к плоской задаче:

d x d n d z d z

d x

d x

I I dz У

d 2 x   л

+ n --у = 0 . dz²

найти показатель преломления n ( x ) .

Из (6) можно также найти уравнение лучей при заданном n ( x ) :

z

x

=J

d x ‘

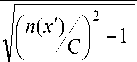
При z = 1 и C = n (0) из последнего равенства следует полученное в [1] выражение для самофокусирующей среды:

n ( x ) =

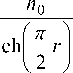
С другой стороны, для случая n = n ( z ), из

В работе [1] рассмотрен случай для при этом (3) переходит в:

d² x

^d n =    /d z ²

ⁿ d x 1 + ( d x4 ) 2

n = n ( x ) ,

Далее полученное уравнение интегрируется для семейства лучей и функции z=z(x) .

уравнения (3) можно получить:

d2 x
dln n	d z 2
d z     d x d z	1 +f d x 12 _ ^ d z J _

Далее, аналогично предыдущему рассмотрению, можно получить выражения для коэффициента преломления и для семейства лучей:

n ( z ) = C ^f d z ) + 1

^1 1 d x J

,

x

z

-J

dz

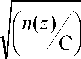
- 1

Тогда вместо уравнения () получим:

д In n . . д In n a (z, 5) + b (z, 5)        + c (z, 5)        - 0,      (18)

д z           д 5

Для общего случая при n - n ( x , z ) из уравне-

где:

ния (3) можно получить следующее выражение:

. дlnn дlnn f (x,z)      — дz    дx

+ q ( x , z ) - 0

d2x a (z, 5) - —2-dz

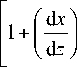
где

d x

f(x, z) -    , dz

d² x

x - x ( z , 5 )

q ( x , z )

d z ²

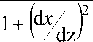
b ^{( z} , ⁵ ) ^- l x д z

x - x ( z , 5 )

В работе [2] предложен путь нахождения общего решения уравнения (12), которое должно зависеть от некоторой произвольной функции.

В уравнении (12) переменные x и z не незави-

симы, т.к. это уравнение выполняется вдоль луча x - x ( z ). Тогда производную в (12) можно вычис-

лить как производную от сложной функции:

д ln n _ д ln n ( x ( z ), z ) d z

д x         д z     d x

В этом случае (12) примет вид:

f ( x ( z ), z ) dn n + P ( x ( z ) ) dn n + q ( x ( z ), z ) - 0, ⁽¹⁴⁾ d z           d z

дx д5 д5 | дz дz дx J     , .

x - x ( z , 5 )

Если не предполагать возможность разрешения уравнения семейства лучей x - x ( z , 5 ) относительно s , то можно получить другое уравнение для ln n также через независимые переменные z и s:

д ln n         д In n a (z, 5) + b (z, 5)        + c(z, 5)        - 0 ,(20)

дzд где ~(z, 5) --^dS5)   .(21)

C ( z , 5 ) -

где p ( x ( z ) ) -

^^^^^^B

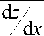
Решение этого уравнения легко записать в виде:

ln n ( x ( z ), z ) _- ^zz      q ( x ( z ' ), z ') d z '

ⁿ n ⁽ x ⁽o^{),o )     J} p ⁽ x ⁽ z ') ) + f ⁽ x ⁽ z 'X z ') ,

или окончательно:

n ( x ( z ), z ) - n (0) • exp l

I + C ,

1    (dx где C - - arthl

2     ( d z

z - 0

arth – арктангенс гипербо-

лический.

Это решение справедливо только вдоль луча x - x ( z ). Чтобы найти показатель преломления ГОЭ

3. Ход лучей в ГОЭ

Для расчета ГОЭ, в первую очередь необходимо задать ход лучей внутри элемента таким образом, чтобы из заданного во входной плоскости распределения интенсивности и наклонов лучей, получить максимально близкое к требуемому распределение интенсивности и наклонов в выходной плоскости элемента. Очевидно, что данная задача решается не однозначно: можно построить множество семейств лучей, удовлетворяющих заданным условиям на входе и выходе. Задачу можно разделить на две части: однозначное определение координаты (отсчета) на выходе для каждого конкретного луча, и собственно сам алгоритм построения траектории луча внутри ГОЭ.

как функцию двух координат n - n ( x , z ), перейдем в уравнении (12) от зависимых переменных x и z , к независимым переменным x и s , где s – непрерывный параметр определяющий конкретный луч из семейства лучей плотно заполняющих ГОЭ: x - x ( z , 5 ). Предположим, что функцию x - x ( z , 5 )

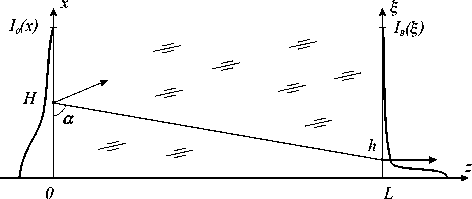
Рис. 1. Однозначное сопоставление входного и выходного лучей.

можно разрешить относительно 5 : 5 - 5 ( x , z ), и рас-

смотрим функцию ln n ( x , z ) как функцию двух независимых переменных x и 5 : ln n ( z , 5 ( x , z ) ) . Тогда производные в уравнении (12) можно переписать как производные от сложной функции [2]:

д ln n ( z , 5 ( x , z )) _ д In n   д In n д 5

дz ” дz дs az ’ д In n (z, 5(x, z))   д In n д5

д x       ~ д 5 д x ’

3.1. Взаимно–однозначное соответствие входной и выходной плоскостей

Для однозначного определения координаты (отсчета) заданного луча на выходе, присвоим каждому лучу во входной плоскости энергетический вес равный значению интенсивности I₀ ( x ) в конкретной точке (отсчете) входа. Аналогичным образом зададим распределение энергетических весов I B ( ξ ) в ка-

N p

I в (^ p ) ^ Z I о ( X k ), P = 1, M , N 0 = 0, (22) k = N + 1 p - *

где xp, ^k - координаты точек во входной и выходной плоскостях, Np-Np-1 - число лучей пришедших в M точку (отсчет) ^p , Z Np = N - общее число лу-р=1

чей.

Очевидно, что в результате дискретизации в некоторых отсчетах суммарный энергетический вес окажется несколько большим требуемого значения, в других - меньшим, однако необходимым является выполнение равенства:

MN

Z I b ( 5 k ) = Z I о ( X k ),                     (23)

k = 1              k = 1

Здесь и далее предполагаем, что А х = А^ - шаги сетки на входе и выходе одинаковы.

Зная номера входного и выходного отсчетов, можно определить угол направляющей луча, соединяющего две точки на входе и выходе ГОЭ (Рис. 1.). Если H - номер отсчета на входе, h - номер отсчета на выходе, А х - шаг сетки по оси х , L - длина оптического элемента, то:

^{tg a}= ( н^ -                   <²⁴>

3.2. Алгоритм построения траектории луча

Очевидно, что при всех возможных комбинациях углов у лучей на входе и выходе ГОЭ, принципиальное отличие имеют два случая: случай разнонаправленных лучей (Рис. 2.) и случай сонаправлен-ных лучей (Рис. 3.).

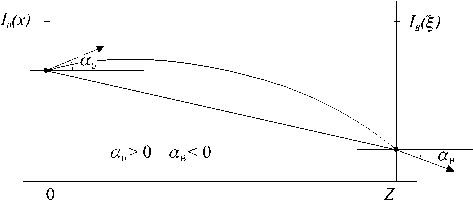
Рис. 2. Случай разнонаправленных лучей.

В первом случае необходимо плавно сменить угол у луча с а ₀ до а_В на протяжении длины элемента L , т.е. за Z отсчетов сетки. Таким образом (в случае а ₀ >  0, а_В <  0), угол наклона луча на каждом шаге будет задаваться формулой:

^a i "  ^а 0

« о^Ы

Z

■ i .

В случае сонаправленности, лучи будут претерпевать перегиб (Рис. 3.).

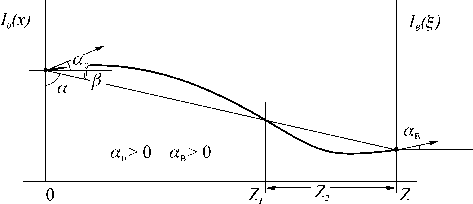
Рис. 3. Случай сонаправленных лучей.

Для обеспечения плавности изменения угла вдоль хода луча координата точки перегиба должна зависеть от соотношения входного и выходного углов:

Z 1 = ° о_

Z 2   « в

где Z ₂ = Z - Z 1 .

Тогда координата Z ₁ точки перегиба луча определится по формуле:

Z 1 = ^{Z a}     ,                              (27)

« в ^{+ а} о

Таким образом, при а0 = аВ последнее равен- ство переходит в очевидное:

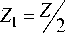
Тогда, если а - угол у направляющей луча, вычисленный по формуле (24), угол в = п /2 - а, то за Z 1 шагов необходимо сменить угол у луча с «о до 2Д. Таким образом (в случае а0 > 0, аВ > 0), угол на каждом шаге от 1 до Z 1 бу дет задаваться формулой:

^a i = ^а о

а ₀ + 2 в Z 1

Далее за Z ₂ шагов необходимо сменить угол у луча с 2 в до a_B , соответственно угол на каждом шаге от Z 1 +1 до Z будет задаваться формулой:

« = 2 в - 2^ °- ■ i .                   (30)

Z 2

4. Расчет показателя преломления ГОЭ

Рассмотрим уравнение (20), вычисляя величины a(z, 5), b(z, 5) и ~(z, 5), исходя из заданных нами траекторий лучей, можно определить величину n(z, 5), что позволит полностью рассчитать требуемый ГОЭ. Так как уравнение       (20) записа но относительно z и 5, и мы не предполагаем разрешения уравнения семейства лучей относительно 5, то, очевидно, для каждой конкретной точки с координатами х и z можно получить несколько значений коэффициента преломления n(х, z). Возникшую неоднозначность можно устранить, например, путем усреднения полученных в точке (х, z) значений коэффициента преломления:

n ( х , z ) = —Z n ( х ( z , 5 k ), z ) ,                   (31)

P k = 1

где p – число значений коэффициента преломления. Далее для удобства записи переобозначим:

n = n ( x , z ), a = a ( z , s ), b = b ( z , s ), c = ~( z , s ).

Для численного решения уравнения (20) зададим сетку с узлами в точках ( s , z ) = ( kh , 1т ), h : 0 … k где             – шаги сетки.

т : 0... i

Запишем разностную схему:

i i n k - nV . i n k + i - n k

ak + bk---------+ ck----;----= 0,         (33)

т            h nk = n 0( kh).

Отсюда:

ния коэффициента преломления заданного ГОЭ в координатах s и z .

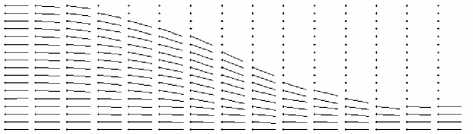
Рис.4. Рассчитанные траектории лучей (верхняя полуплоскость).

l k

b k hn k 1 - c k Tn k - 1 - a k hT ^b k h - c k ^T

2 ^и

входя-

щие в величины a , b и c зададим следующими разностными выражениями:

dx _ Ax i+1 - Ax i dz         Az     , d2x ~ Axi+1 - 2Axi +Axi+1

d z ²             A z ²

dx    Ax i+i -Ax i d s ”             •

Очевидно, что при dx/ds=0, величина c обращается в бесконечность. Подобная ситуация возникает в случае слияния двух соседних лучей в точке ( x , z ) , и в этом случае разностная схема примет вид:

n

l k

= n k - 1

a k ^{T b} k^l

5. Численное моделирование

Для реализации численного расчета ГОЭ была написана программа с использованием среды программирования Borland ® Delphi ® . В рамках единой программы объединены средства задания распределения интенсивностей на входе и выходе, расчета траекторий лучей и расчета показателя преломления ГОЭ. Программа позволяет интерактивно менять различные параметры, оказывающие влияние на расчет, вид применяемых разностных схем, а также позволяет представлять полученные результаты в различных вариантах.

На рис. 4 показан ход лучей в ГОЭ (верхняя полуплоскость), переводящего плоский пучок с постоянной интенсивностью на входе в плоский пучок меньшей ширины, также с постоянной интенсивностью, на выходе. На рис. 5 показаны (в псевдоцветах) соответствующие энергетические веса, переносимые по рассчитанным траекториям лучей. На рис. 6 показаны (в псевдоцветах) полученные значе-

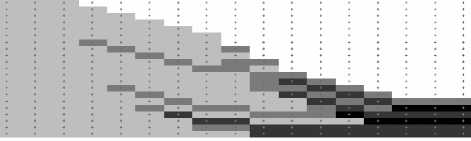
Рис. 5. Энергетические веса переносимые лучами вдоль рассчитанных траекторий (верхняя полуплоскость, псевдоцвета).

Рис. 6. Коэффициент преломления ГОЭ в координатах s и z (верхняя полуплоскость, псевдоцвета).

Параметры расчета: длина элемента L = 30 мм., ширина пучка на входе h вх = 8 мм., на выходе – h вых = 1,5 мм., количество отсчетов: по вертикали – 16, по горизонтали – 14.

Заключение

Получены следующие результаты:

• •    рассмотрены различные варианты зависимости показателя преломления от пространственных координат, получены соответствующие им аналитические выражения;

• •    разработаны алгоритмы построения траекторий лучей внутри ГОЭ для различных сочетаний входных и выходных углов;

• •    поставлена и решена разностная задача для общего уравнения.

• •    составлено программное обеспечение для реализации численного расчета ГОЭ.