Расчет характеристик виброактивности буксы вагона
Автор: Захезин A.M., Иванов Д.Ю.
Рубрика: Расчет и конструирование
Статья в выпуске: 14 (54), 2005 года.
Бесплатный доступ
Рассмотрена математическая модель виброактивности буксы вагона при его движении по рельсам. Представленная модель позволяет учесть эксплуатационные нагрузки в вертикальном и горизонтальном направлениях. Эксплуатационные нагрузки рассчитаны на основании реальных отклонений рельсовых нитей от их осей.
Короткий адрес: https://sciup.org/147151353
IDR: 147151353 | УДК: 625.2.001.24,
Текст научной статьи Расчет характеристик виброактивности буксы вагона
Виброакустическая диагностика машин и оборудования получила широкое применение в силу ряда преимуществ. Такими преимуществами являются безразборность, одинаковость структуры вибрации типового оборудования и его комплектующих, возможность использования разработанного аппарата спектрально-корреляционного анализа и декрементов случайного процесса вибрации. На этой основе дальнейшее развитие виброакустической диагностики с целью контроля технического состояния на стадии изготовления и монтажа, на стадии эксплуатации является актуальным. Кроме того, широкий класс характеристик случайной вибрации позволяет оперативно определять возникающие неисправности и определять ресурс работы машин по времени наработки.
Чувствительность вибрации механических систем к небольшим изменениям их состояния делает анализ вибраций мощным средством диагностики. Так как диагностическая информация содержится в случайной вибрации механических систем и отдельных ее комплектующих, то в процессе диагностирования должны сравниваться характеристики вибрации «первоначального состояния» с «текущими». Для успешного решения задачи вибродиагностики необходимо рассмотреть следующие вопросы: выбор типовых звеньев механической системы, выбор интервала периодичности освидетельствования механической системы, выбор места установки датчиков, выбор типа измерений и вида характеристик случайного процесса вибрации, задание типовых эксплуатационных режимов работы, выбор характеристик ресурса работы и состояния механической системы.
Отсутствие экспериментальной информации о техническом состоянии буксы предполагает на первом этапе воспользоваться математической моделью, которая позволит получить характеристики виброактивности буксы вагона с некоторым приближением.
Аналитическое исследование пространственной виброактивности транспортного средства (ТС) проводится на основе математического описания его расчетной схемы, которая отражает с некоторыми допущениями особенности динамики взаимодействия его частей под действием эксплуатационных нагрузок. -
Исследование виброактивности ТС в низкочастотном диапазоне позволяет существенно упростить расчетную схему и представить его в виде динамической системы, состоящей из ряда твердых тел, соединенных безынерционными упругими и демпфирующими элементами. На относительное перемещение масс накладываются ограничения, характер которых зависит от конструктивного выполнения подвески.
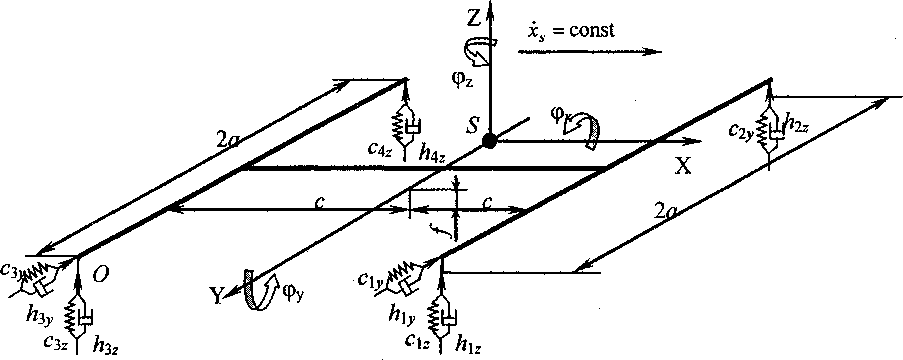
Дифференциальные уравнения движения составим в системе координат Sxyz (см. рисунок) с помощью уравнений Лагранжа 2-го рода.
Положение ТС определяется обобщенными координатами:
qt=(2$.у$.Фх>ФУ.фг)^=х-^
где zs,ys - перемещения центра масс ТС от горизонтальной и вертикальной плоскости;
<рх, фу, фг - углы поперечного, продольного крена и угол рыскания.
Кинетическая энергия ТС тогда запишется:
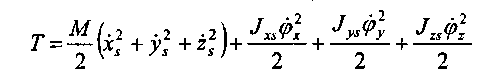
Обозначим соответственно:
сжатие рессорных комплектов: сдвиг рессорных комплектов по оси у:
51х = Zs -Сфу "«Фх ~Л2, ^/=^4-^-/^-^,
52z =2s -сфу уаф,-Ц,, 8гy=ys*cфI*fфx-hXy, ^
53z=zs +сфу-афх-Ц2, 83у = ys-сф2 +/фх-Цу,
Ц2 =zs +ефу +афх -Ц2, 84у=ух-сфг-^Афх-Н3у, где hX:, к2г, Ц2, h4z - возмущение по оси z; ИЛу, Цу - возмущение по оси у,
. Перемещение точки О:
х0=х$-/фу, Уо=Ух-сф2+/фх, z0 =zs+Сфу-афх.(4)
Согласно определения обобщенные силы запишутся в виде: QB=FXz+F2z+F3z+F42+F„ Q^ =-FXza + F2za - F3za + F4za, е^=0’ Qw =-FXz^F2z c-F3zc*F4z с.
Вертикальная составляющая полной силы по оси 2 ву-й подвеске запишется как ^-«Д+Г,^, (/ = 1,2,3,4),(6)
где cj2 - жесткость у-й подвески; rjz - коэффициент сопротивления у-го амортизатора. Горизонтальная составляющая полной силы по оси у ву-й подвеске запишется как
Fjy =cjy5jy *rjAy, (/ = 1,2,3,4),(7)
где cjy - жесткостьу-й подвески на сдвиг; г/У - коэффициент сопротивленияу-го амортизатора.
Приведем преобразование входных воздействий к виду: qAO=Qhz^h2ZW qA^r')=th3z *h4z^2,
4y^ = hXy, qy(t + T) = h3y = кХуф*т\(8)
^=^х-Ц^а, ^(Г4-г) = (^г-/z4z)/2«, где т = -2с/х - запаздывание возмущения.
Дифференциальные уравнения движения ТС в продольной плоскости примут вид: ап 2S + а;, z, + 3], zs + а;2 фу + а12 ф, = b;, qAO + Ьи qz<0 + bj2 qz (t + г) + b12 qz (Z + г), a2i ^ + »21 2S + a22 фу + a22 фу + a22 фу = b^ qz^ + b2, q2(.O + b'22 qA(+ t) + b^ q2(t + r), a33 Ф, + азз Фх + азз Фх = b21 ФАО + b31 ФА0 + Ьз2 ФА1 + г) + b32 фхф + 7), а41 Ух + а41 Ух + а41 К + а45 Фг + а45 Фх = ^, 1^(0 + Ь41 ^(0 + Ь42 ^(Z + г) + Ь42 /^/Z + г), ам Ух + а54 Уз + а55 Фх + а55 Фх + а55 Фх = Ь'51 ^у (0 + Ь5, ^у (Z) + Ь'2 Д/Z + г) + Ь52 ^ (Z + г).
Захезин М.А., Иванов Д.Ю.
В полученных уравнениях движения коэффициенты имеют следующие выражения:
ап — М, аи -2(rlz + r3z), au-2(с1г+c2z), а;2 - 2c(r3z - rlz), а12 = 2c(c3z - clz), a2i = ~2cO"]Z + f3z ), ai2 =а12, a22 =^,a'22 =2c2(rlz + r3z), a22 =2c2(cu + c3z), азз = Л^азз =2a2(rlz +r3z),a33 =2a2(clz + c3z), a41 = 2(rv + Лу X a4i = 2(cv + c3y ), a45 = W\y + %Y a45 = W\y ~ C3y X a54 =a45’ a54=a45 = a55 =Л.^а55 =2c2(rly + г3Да55 = 2c2(cly + c3y),
b'n-2rlz, bn-2clz, b'12 = 2r3z, b12 = 2c3z, b*2i=2crlz, b21 =2cclz, b'22 =-2cr3z,b22 = -2cc3z, b31=2a r]z,b3r = 2a c!z, b'32 =2a2r3z,b32 = 2a2c3z, ^’4i=2rly, b41 = 2cly, b'42 = 2^3^, b42 = 2c3y, b'5!=-2cr^,b51 =-2ccly, b’52=2cr3y,b52 =-2cc3y.
Здесь a", a*, a - коэффициенты соответственно инерции, демпфирования и жесткости; b', b - коэффициенты, преобразующие возмущения и их производные в обобщенные силы.
Применив преобразования Лапласа при нулевых начальных условиях и отнеся все к соответствующим входным воздействиям получим уравнения для передаточных функций:
^Иаи + »ап +а11)+^(^ап +ai2)=b;is + b11 + b[2se~®T +ЬА2$е-ЙТ;
^м(^ап + an) + ^G2a52+sa22 +a22)=b'21s + b21 + b^se"^ + b^e^;
^52азз+5азз+азз)=Ьз15 + Ь31+b32se-®r+b32s^ (11)
^(s2a41 + sa41 + a41)+^(sa'45 + a45) = b4]s + b41 ч-Ь^Ав-^ + ^236"^;
^(5354 +з54) + ^(а2з"5 +S3'55 + 3 55)=b51A + b51 +b525e~OT +b52se""®T,
Zs(i®) Ф/i®) Фх(^) ш Y/i®) Ф2(ю)
где W= ——-, W= —--, IT =—^—-, W= ——-, Л"=—^—--чзстотные qz(ito) qz(i®) q^ico) qy(i®) qy(i®)
хзрзктеристики обобщенных координзт.
Используя одностороннее преобрззовзние Фурье получзем систему алгебраических уравнений с комплексными коэффициентами, по которой из первых двух уравнений определяем частотные характеристики по обобщенным координатам zs, <ру, третье уравнение определяет частотную характеристику по обобщенной координате фх ; и, наконец, последние два уравнения определяют частотные характеристики по обобщенным координатам у.„ <рг.
Теперь мы можем получить характеристики виброактивности в любой точке ТС. Например, в точке расположения буксы спектральная плотность виброускорения по соответствующим координатам определится следующим образом:
sx=®7K! sqA®\
^= sz=^4{[кГ +Н^|2]^(®)-^Г^(й>)}, где Sqz, Sqy, S^ - спектральные плотности входного воздействия. Формулы являются основным соотношением в частотной области, дающим решение задачи виброактивности ТС, т.е. характеризуют прохождение стационарного процесса возмущений от профиля пути на стационарную линейную систему. В частности формулы (12) позволяют решить задачу вибронагруженности буксы на стадии проектирования. В общем случае математическая модель вертикальных и боковых возмущений может быть представлена в виде [1-6] (см. таблицу): «верт rr I с . оверт . оверт . о ^(й) — ^qz4 ^уа *• ^стык "^ ^пути ^ ^ колес» 16ОК _ обоК, О '(со) ~~^стык ^^у» 'qz qz «4 + 2(а2-^W + [(«? + РЪ^Аг ’ , 4а а2 'усг -^уа , т 2x2 ’ Я- (<92+ а ) где сверт _ I Г ^ 0Uln2j 2 2 V ГО Т 161п2. ^-т2пУ,5(ю-пго0) + ст2п о2 с««™ °путъ L . ' С ° колес го2 а2 „ =—5(ю~юх), ^бок ^стык = ^Т0 — Г °Uln2j / _,2_2 \2 ГО Т ехр-- 161п2 2л ■ —т. Л ' ^РСго-пго^ + ст2 , п=1 _ Оценки и их доверительные границы Объект -участок пути Коэффициенты а ' Р Dqz,^ Среднее значение и доверительные ' границы для него 1 а =0,071 (0,0705...0,0714) P^,22Q (0,2116...0,2284) II?z =129,33 2 а =0,064 (0,0625...0,0654) Д =0,053 (0,0526...0,0534) I5qz =187,55 3 а =0,019 (0,01857...0,01905) Д =0,064 (0,0659...0,0661) Д, =222,50 Среднее квадратическое отклонение 1 а„=0,0266 о^=0,1150 ^Dqz =79,025 2 а„=0,0475 Ср =0,0256 cDq2 =91,270 3 аа=0,0068 о^=0,0576 0^=113,140 Максимальное вероятностное значение 1 max а =0,1530 max Р =0,565 maxD,z=461,36 2 max а =0,2060 max ^=0,129 maxZ>gz=1468,65 3 max а =0,0394 max р =0,237 maxD9Z=113,14 Максимальное значение, полученное обработкой эксперимента 1 ^=0,120 1,^=0,3900 £)9,max=262 2 ^=0,152 ^max=0,0990 S^max^lS 3 42^^=0,061 lmax=0,0152 Dqi ЦЙВГ335 Минимальное значение, полученное обработкой эксперимента 1 й^т=0,035 )?min=0>08 2)9zmin=54,43 2 . ^min™0>015 /?min=0,022 Dqz min=64,20 3 Отпт=0,012 ^min=0,052 ^(?Z nun—61,07 . При использовании численных методов расчета характеристик виброактивности ТС необходимо иметь в виду, что динамические модели отражают динамические свойства объекта в ограниченном диапазоне частот. Поэтому при определении дисперсии виброускорения верхний предел интегрирования можно ограничить значением <утах, несколько превышающим высшую собственную частоту колебаний динамической модели ТС. Учитывая, что низкочастотные колебания ТС на частоте возмущения в два и более раз меньшей собственной низшей частоты имеют малую интенсивность, можно ограничить и нижний предел интегрирования значением tomin. Таким образом, дисперсия виброускорения по осям декартового пространства, в частности в точке расположения буксы, определится следующими формулами: 1 ®22 । Dx — ^4f\w4sqMM Л ®21 1 4,42 I |2 С И^ I |2 Г @322 Dy=- ^Дз^® — ]®4\wpx\ 8чд®^®* — M^J svA®W, ^ <ы41 ^ <у51 ^ t»31' 1 ti>12 - ' p 6)22 j л °322 Dz=- ^4\Wzs\2Sqz(®W + - М^,| Sqz(®W— j®4^ SvxWco; (14) ^zall -^«21^ o31 i iо max о , .min па ,_max n i -.min,^max d)ll = 0)xs ,6)12 = ^ ,б)21 = й)фу , ti>22 = fi>,со31 = й)фХ ,б)32 = 0)фх , ®41 = ®v, , ®42 = ®„. , 051 = 0,., , 052 =. ya ' ya zz Так как внешнее воздействие на ТС задается в сравнительно узком диапазоне частот, выражение (14) позволяет получить достоверный результат и в том случае, когда входные воздействия аппроксимируются не дифференцируемыми выражениями (13). Дисперсии ускорений (14) можно использовать как базовые, увеличение которых в эксплуатационных режимах работы в первом приближении информирует о зарождающихся дефектах подшипников буксы.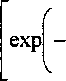
Список литературы Расчет характеристик виброактивности буксы вагона
- Бук В.А., Захезин A.M. Определение прогиба подкранового рельса при движении по нему сосредоточенной нагрузки//В сб.: Динамика машин и рабочих процессов. -Челябинск: ЧПИ, 1983.
- Бук В.А., Захезин A.M. Статистические характеристики рельсовых путей и их аппроксимация//В сб.: Динамика машин и рабочих процессов. -Челябинск: ЧПИ, 1980.
- Камаев В.А. Оптимизация параметров ходовых частей железнодорожного подвижного состава. -М.: Машиностроение, 1980.
- Иванов Д.Ю. Диагностика подшипников скольжения//В сборнике докладов и материалов II научно-технической конференции «Вибрационные машины и технологии». -Курск: КГТУ, 1995.
- Юшина О.П. Феноменологический подход к проблеме контроля технического состояния подшипников качения//В сборнике докладов и материалов II научно-технической конференции «Вибрационные машины и технологии». -Курск: КГТУ, 1995.
- Zakhezin A.M., Malysheva T. V., Ivanov D. U. The evolution of the influence of elastic-viscous properties of a crane-runway on the transport-technological vehicle (TTV) random fluctuations. Proceedings of the APVC-98, 1998.


