Расчет хода псевдолучей через дифракционные структуры, выполненные на сферической поверхности

• 1.    Введение

• 2.    Точные лучевые соотношения

В работах [1-3] описана методика и приведены формулы расчета хода псевдолучей лучей (т.е. лучей, траектории которых рассчитываются в приближении заданного порядка малости) через вращательно-симметричные системы, включающие радиально-градиентные и дифракционные линзы. В этих работах предполагалось, что структура дифракционной линзы (ДЛ) выполнена на плоскости. Однако известно, что размещение структуры ДЛ на сферической поверхности открывает возможность управление комой линзы (вплоть до ее устранения) независимо от величины сферической аберрации, расположения предмета и зрачка [3]. Очевидно, что использование ДЛ на сферической поверхности в составе гибридной оптической системы может существенно расширить ее коррекционные возможности, поэтому целесообразно распространить методику расчета хода псевдолучей на такие элементы.

Для получения формул расчета хода псевдолу-ча необходимо иметь представленные в аналитическом виде точные соотношения, связывающие параметры дифрагировавшего и падающего на ДЛ лучей. Такие соотношения для элементов, структура которых размещена на поверхностях произвольной формы приведены в работах [4, 5]. Точные лучевые соотношения следует разложить в ряды по степеням входных параметров луча. В результате после разложения и соответствующей перегруппировки параметры луча на выходе из ДЛ будут описываться степенными рядами, состоящими из слагаемых различных порядков малости относительно параметров луча на входе в оптическую систему. В результате ограничения рядов конечным числом слагаемых будут получены выходные параметры псевдолуча, вычисленные в требуемом приближении. С целью упрощения вышеописанной процедуры точные лучевые соотношения целесообразно представить в виде наиболее удобном для последующего разложения.

Требуемые лучевые соотношения получим для представляющего наибольший практический интерес случая, когда размещенная на сферической поверхности кольцевая структура ДЛ симметрична от-

носительно оси, проходящей через центр сферы и являющейся оптической осью линзы. Введем две прямоугольные системы координат. Одна из них - K - система с началом координат, совмещенным с вершиной сферической поверхности, и осью Z , совпадающей с оптической осью. Вторая - локальная K - система, ее началом координат является точка падения луча на сферическую поверхность, а ось Z совпадает с нормалью к поверхности в этой точке. В K - системе уравнение сферической поверхности, на которой размещена структура ДЛ, имеет вид [6]

z

= (V с

- V1 -(c р)2

где с - кривизна сферической поверхности, р = V x ² + у ² .

В этой же системе координат направляющие косинусы оси Z (составляющие орта k) описываются выражениями т       т       т kx = - cx, ky = - су, kz = 1 - cz .              (2)

Что же касается двух других ортов i и j , то их составляющие легко найти, воспользовавшись очевидными соотношениями

i ■ j = 0, i ■ k = 0, j ■ k = 0

^{т 2}= 1, ^{т 2}= 1

.

Поскольку (3) представляет собой систему пяти скалярных уравнений с шестью неизвестными, то одна из проекций орта ^j или j может быть выбрана произвольно. Положим, например,

Jx = 0,                                            (4)

т т - тогда другие составляющие ортов j и i будут оп-

ределяться соотношениями

т

jy =

т kz т2 т2

^ky ^{+ k}z

т

Jz =

т

ky

т

k

т

y

+ k.

z

~ i x

~ ~  ~ ~ kzjy - kyjz

iy

iz

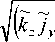
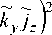
+ к 2 j

kj xz

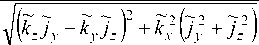
kx jy

.

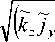
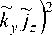
k2 (jy2

Составляющие ортов i , j и к образуют

матрицу

А =

~

ix

~

~ ~ i y i z

~ ~

jx jy h

~ ~ ~ kx kv kz

V x y z у

,

с помощью которой можно перейти от составляющих любого вектора, определенных в К - системе к составляющим этого же вектора, определенным в К - системе. Обратный переход производится с помощью транспонированной матрицы А’ .

Целесообразность использования локальной К - системы обусловлена тем, что именно в этой системе справедливы простые соотношения, связывающие направляющие косинусы дифрагировавшего и падающего лучей с производными эйконала записи структуры ДЛ:

~ d G ~     d Gn

ax = a x + m Ц ^F0,  ay = a y + m Ц - оx                  dy

~f         ~<2 ~<2

az = 1--ax -ay

где m - порядок дифракции, ц = X/X ₀ , X - длина волны света, падающего на ДЛ, Х ₀ - длина волны записи (в дальнейшем будем полагать, что m = - 1 и ц = 1).

Производные же эйконала записи можно выразить через направляющие косинусы нормалей к двум фронтам записи, по крайней мере, один из которых является асферическим. В результате соотношения (8) приобретают вид

~f ~   ~   ~

аx = аx -alx +а 2x,

a _y

= a y

^a 1 y

^{+ a} 2 y

~f

a z

1 -~ X

x

a

y

Г , (9)

Направляющие косинусы, входящие в правую часть выражений (9), изначально известны только в К - системе. В частности, направляющие косинусы нормали к первому (сферическому) фронту записи определяются выражениями

x

s V (р/5 )2 + (1 - z/s )2

s V (р/s )2 + (1 - zis )2 a1 z = V1 - aL - a2y

а направляющие косинусы ко второму (асфериче

скому) фронту записи - соотношениями

x

a 2 x =      /                    . +

s' (р/s') +(1 - z/s')

1 , 2 3 , 4

⁺ y b 3 ^{р  +} yyb 5 ^{р  -}...

2        8

a 2 y =      /                       + Г , s' (ppls2F'1--zis2F

1 ,     2     3 ,     4

• +2b3р + 8b5р -...

• a 2 z = V1 -a 2 x -a 2 y

3. Схема расчета хода псевдолуча

где - s и s' - отрезки записи, b ₃, b ₅, ^ - коэффициенты асферический деформации третьего, пятого и т.д. порядков [5].

Таким образом, чтобы найти направляющие косинусы дифрагировавшего луча в К - системе необходимо вначале направляющие косинусы падающего луча и нормалей к фронтам записи, известные в этой системе, пересчитать с помощью матрицы А [см. выражение (7)] в К - систему. Затем, используя соотношения (9), получить направляющие косинусы дифрагировавшего луча в К - системе и совершить с помощью транспонированной матрицы А обратный переход в К - систему.

Рассмотрим теперь, как можно использовать вышеприведенные соотношения для расчета хода псевдолуча через структуру ДЛ, размещенную на сферической поверхности. Для определенности ограничимся приближением пятого порядка малости.

Высоту и наклон псевдолуча в точке его падения на поверхность ДЛ опишем векторами S и T . Вектор S имеет составляющие ( x , y , 0 ) , вектор T - составляющие ( T_x , T_y , 0 ) , где T_x и T_y - направляющие тангенсы луча связанные с направляющими косинусами луча соотношениями

^Tx = ^a x /^a z , ^Ty = ^a y a zz . ⁽¹²⁾

Векторы S и T являются функциями двух зрачковых векторов, определяющих высоту и наклон луча во входном зрачке оптической системы, и могут быть представлены в виде суммы слагаемых

первого, третьего, пятого и т. д. порядков малости относительно модулей этих зрачковых векторов:

S = S ⁽¹⁾ + S ⁽³⁾ + S ⁽⁵⁾ + ...

T = T ⁽¹⁾ + T ⁽³⁾ + T ⁽⁵⁾ + ..

Введем три инварианта вращения ei — T2, e2 = T■ S , e3 = S2                     (14)

и, используя соотношения (13), запишем их в виде е     (2) .-(А) e1   e1   + e1   + e 2 — e 22) + e 24) +... -,                                   (15) e3 — e 32) + e 34) + ... где

e i(2) 4® )2 + 4 )2    | ei(4) = 24 TX3^ + Ty11 Ty33) ’

e 2 ²⁾ = x ⁽¹⁾ T® + y ⁽¹⁾ T y ¹

e ⁽⁴⁾ = x ⁽¹⁾ T³³³ + x ⁽³⁾ T <« + y ⁽¹⁾ T + y ^{(3) 4}

2               x              x * У * У

e32) =(x(1) )2 +(y(1) )2       | e 34) = 2(x(1) x(3) + y(1) y(3) f

Разлагая уравнение (1) в степенной ряд и используя соотношения (14), (15), координату z точки пересечения луча с поверхностью ДЛ можно представить как

z — z ⁽²⁾ + z ⁽⁴⁾ + ... ,

где

z ⁽²⁾ = 2 c       z ⁽⁴⁾ = ¹ ce f⁴) + ¹ _с ³ (   ) 2 . (20)

Далее, поскольку направляющие косинусы падающего на ДЛ луча связаны с его направляющими тангенсами соотношениями

а = Т / 21 + Т ² + Т ²

xx    x y а у — Ty/V1 +   + Т -, а z = ^1 + Tx3 + Ty

то после разложения в степенные ряды получим

а _x — а ^ ¹⁾ + а ^ ³ + а^³ + ... а у = а У > + а У + а У + ...

а _z = 1 + а^³ + а У³ + ...

где

а (1)_7(1) а(3) _7(3)_17(1) (2)

^а x ^— T x , ^а x ^— T x 2 T x ^e 1

а = T <⁵⁾ - 2 t ⁽³⁾ e_x ⁽²⁾ + t ⁽¹⁾Г 3 ( e ⁽²⁾ ) 2 - 1 e_x ⁽⁴⁾ x x 2 x 1 x I 8 ^{x 1 7}      2 ¹

(1)       (1)

^а y У у )

а У ³⁾ = Т

-

1    (1) (2)

₂ T y e 1

а < «- if-1T^ ) + Т У" 3 ( , ') — 1 e ( ⁴⁾ 2                L 8         2

- ; (23)

И—- 1 e ™, а < *> = - 1 e ( ⁴⁾ + 1 ( e i ² -) ² .       (24)

Аналогично, разлагая в степенные ряды уравнения (10) и (11), можно представить в виде сумм величин различных порядков малости направляющие косинусы нормалей фронтов записи:

а = а (¹)+а(³) + а(⁵)+ I ^а px ^а px ^{+ а} px ^{+ а} px ⁺ ...

а   = а (1)+а(3) + а(5)+   > а py а py 1 а py 1 а py 1 ...

а pz = 1 + а⁽ pZ ⁾ + а⁽ p ⁴⁾ + ...

( p = 1 — 2 ) .

Далее в виде сумм величин различных порядков малости представим составляющие ортов k , j и i . В частности, из выражений (2), (13) и (19) получим, что составляющие орта k ^j можно записать как

где

j k

x

₌ £0)+ ~(3) ₊ ~(5) ₊ x x x ^...

k y = k® + k(³³ + k ( ⁵ + ...

к, = 1 + к?³ + к(⁴³ + ...

кТ = x	- cx (1),	к ^3) = x	- cx (3) ,	(5) x =	- cx (5) ;	(27)
~ ( 1) = кУ	- СУ (1) ,	~ ( 3) = кУ	- cy (3) ,	~ ( 5) = кУ	- cy (5) ;	(28)

k_z ⁽²⁾ =- cz ⁽²⁾ , k_z ⁽⁴⁾ =- cz ⁽⁴⁾ .                  (29)

Аналогично, раскладывая			в	степенные	ряды
уравнения (4)-(6) и используя представим составляющие ортов			соотношения j  j j и i в виде		(26),
j x — 0 ь —: ~ у ( 2)+:~ у 4)+... j ~ z — j ~ z (1)+ j ~ z (3)+ j~ z (5)+ ..	.				(30)
и
j x — 1 + j (2)+ j x (4)+ ... j=j(2) . j(4) 1y    Ly +      +... j z — j (1)+ j (3)+ j z (5)+ ...	-	.			(31)

Затем с помощью матрицы (7) находим составляющие различных порядков малости направляющих косинусов падающего луча и нормалей к фронтам записи. В частности, составляющие направляющих косинусов падающего на поверхность ДЛ луча в K - системе можно записать как

~ X = ~х) + « '^ + ~~ X ^{5 +} ...

~ y = 5® + ~y3) + ay5) + ...>

~ _z = 1 + a z2) + a z 4) + ...

и аналогично для направляющих косинусов нормалей фронтов записи

+ ~ pX + ... + a py + ... (4) _pz + ...

aDX px

~ a py a pz

~ (1)    ~ (3)

a px + a px

~ (1)    ~ (3)

a py + a py

= 1 + a ⁽„² ? + ~ pz

( p = 1 - 2 ) . (33)

Подставляя соотношения (32) и (33) в (9) получаем в виде сумм величин различных порядков малости составляющие дифрагировавшего луча в K - системе

a' x = aX(1) +~X(3) +~X(5) + ... a'y = a'y(1) + ay(3) + ay(5) +... ■,                    (34) ~Z = 1 + aZ(2) +aZ(4) +.. . где

a X( q )	= a X q )	- s ( q 1	+ ȴx
a y q )	= a y q )	-$ ( q 1	+a < q>

+ ...

+ ...

( q = 1,3,5 ) ; (35)

a z(2) = -1 [(^ )2 + (ay1) )2 ’

a zw = — 1 (5,(2) )2 -^ю -swsy3)

Далее, используя транспонированную матрицу A' , находим в виде сумм величин различных порядков малости направляющие косинусы дифрагировавшего луча в K - системе. Наконец на последнем этапе с помощью соотношений, аналогичных уравнениям (12), переходим от направляющих косинусов к направляющим тангенсам дифрагировавшего луча и тем самым находим в виде сумм составляющих различных порядков малости искомый вектор T ' , определяющий наклон луча, дифрагировавшего на структуре ДЛ, размещенной на сферической поверхности.