Расчет хода псевдолучей через оптические системы, включающие дифракционные линзы, структура которых выполнена на асферической поверхности
Автор: Грейсух Г.И., Ежов Е.Г., Степанов С.А.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы компьютерной оптики
Статья в выпуске: 21, 2001 года.
Бесплатный доступ
Методика расчета хода псевдолучей через оптические системы, включающие радиально-градиентные и дифракционные линзы, распространена на системы с дифракционными линзами, структура которых выполнена на асферической поверхности
Короткий адрес: https://sciup.org/14058487
IDR: 14058487
Текст научной статьи Расчет хода псевдолучей через оптические системы, включающие дифракционные линзы, структура которых выполнена на асферической поверхности
В работах [1-3] описана методика и приведены формулы расчета хода псевдолучей лучей (то есть лучей, траектории которых рассчитываются в приближении заданного порядка малости) через вращательно-симметричные оптические системы, содержащие радиально-градиентные элементы и дифракционные линзы (ДЛ), структура которых выполнена на плоской поверхности. В работе [4] указанная методика распространена на случай включения в систему ДЛ, структура которых размещена на сферической поверхности. Данная работа направлена на дальнейшее развитие методики и обобщение ее на оптические системы, содержащие. ДЛ, структура которых выполнена на асферической поверхности.
Расчет хода псевдолуча через такие ДЛ, включает две задачи: прослеживание хода псевдолуча через среду, которая в общем случае может быть ограничена двумя асферическими поверхностями, и определение параметров псевдолуча, дифрагировавшего на структуре ДЛ. Ниже получены формулы расчета, позволяющие решать обе эти задачи.
1. Расчет хода псевдолуча через однородную среду, ограниченную асферическими поверхностями
Ход луча будем описывать в декартовой системе координат, ось Z которой совпадает с оптической осью. Высоту и наклон луча определим с помощью векторов р и г ; при этом вектор р имеет составляющие [ x ( z ), у ( z ),0 ] , а вектор г - составляющие ( е x , е у ,0 ) , где е x и г у - направляющие тангенсы луча, связанные с его направляющими косинусами соотношениями е x = а x /а z и е у = а у /а z .
При распространении луча между к и (к +1) асферическими поверхностями оптической системы луч на входе в среду зададим векторами р к и г к, а на выходе из среды - векторами рк+1 и гк+1. Если zk к+1 есть расстояние вдоль оси Z от точки входа луча в однородную среду до точки его выхода, то очевидно, что векторы р к, г к и рк+1, гк+1 связаны между собой уравнениями р к+1 = р к + zk, к+1г к г к+1 = г к
Пусть dk - расстояние между вершинами k и ( к + 1 ) поверхностей. Тогда
z k , к + 1 = d k + z k + 1 z k ’
где zk - координата точки пересечения луча с k поверхностью в системе координат, связанной с вершиной этой поверхности и, аналогично, zk + 1 -координата точки пересечения луча с ( к + 1 ) поверхностью в системе координат, связанной с вершиной ( к + 1 ) поверхности.
Уравнение асферической поверхности в системе координат с началом в вершине этой поверхности запишем в виде
F (р, z) = cz — 1 + V1 — (cр) 2
-1 ®з(cр)4 -
— ° 5 ( c р ) 6 - ... = 0 ’ (3)
где с - кривизна поверхности в ее вершине, 0 3 , 0 5 , … - коэффициенты асферической деформации поверхности.
Тогда координаты zk и zk + 1 можно определить из выражений
zk = — 1 ск L
- V1 -( ск р к ) 2
+ 8 п!.к ( скрк )4 +
+ 16 ст 5, к ( ск р к ) 6 + ...
zk + 1 = 1
ск + 1 L
V1 -( ск+1р к+1) 2 +
+ 7СТ 3, к + 1 ( ск + 1 р к + 1 ) 4 +
+ 16 ст 5, к + 1 ( ск + 1 р к + 1 ) 6 + ...
.

Уравнения (1), (2) и (4) являются основой для получения формул расчета хода псевдолуча через однородную среду, ограниченную асферическими поверхностями. При их выводе в качестве первого шага представим векторы р к и г к в виде сумм слагаемых первого, третьего и пятого порядков малости относительно модулей векторов, определяющих высоту и наклон луча во входном зрачке оптической системы:
= D (1)+О(3)+О(5) + р k р k + р k + р к + •••
(1) (3) (5)
£ к £ к + £ к + £ к + •••
,
где р®, рк3 и рк5 - составляющие первого, третье го и пятого порядков малости вектора, определяющего положение луча. Обозначения £ ^ - £k5 имеют аналогичный смысл для вектора, определяющего наклон луча.
Из (2), (4) и (5) нетрудно видеть, что расстояние zk к+1 можно представить в виде суммы членов нулевого и четных порядков малости:
, (0) ,„(2) ,„(4) , zk, к+1 = zk, к+1 + zk, к+1 + zk, к+1 + •••
Подставляя (5) и (6) в первое из уравнений (1), получим, что на выходе из среды о =о (Ц + „(3) ,о(5) , р к+1 р к+1 +р к+1 + р к+1 + ••• ’ где
о(1) -o(1)+z(0)
р к + 1 р к + zk , к + 1 £ к
о(3) -o(3)+z(0) „(3) (2)
р к + 1 = р к + zk , к + 1 £ к + z k , к + 1 £ к
О(5) -D(5)+z(0) е(5)+ Z(2) £(3) + р к + 1 = р к + z k , к + 1 £ к + z k , к + 1 £ к +
+ z k , к + 1 £ к
•
Для того чтобы найти слагаемые различных порядков малости расстояния zk,к+1, разложим уравнения (4) в степенные ряды, а результат разложения подставим в (2) При этом воспользуемся уравнениями (7) и (8), введем три инварианта вращения е1 = £ к , e2 = £ к ■ р к , e3 = р к (9)
и, используя соотношения (5), представим эти инварианты в виде e1 = . + e4 + „ e 2 = e 22) + e 24) + „ e 3 = e 32) + e 34) + •••
|
где |
||
|
2 . [.. ? e f) = 2 £ «1. |
£ (3) £ к |
|
|
e 22) р ^ k ”. e ^) = рТ^£ k " +р»> |
• £ k3) |
. • (11) |
|
e 32) = [р*1) ]2- e i4) = 2 р. |
р к 3). |
|
|
В результате получим z (0) = d, zk , к + 1 dk , |
(12) |
|
|
z (2) --(c -c')(2) + z k , к + 1 = 2 ( c k + 1 c k ) e 3 + |
||
|
+ C k + 1 d k 1 e 22) + 1 d k e 1 2 J |
, |
(13) |
2 (4) "-(с, , W4) + z k , к + 1 = 2 ( ck + 1 ck ) e 3 +
_
1 к , _ \3
+ 8 [( 1 + ° 3, к + 1 ) c k + 1
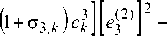
+ c k + 1 d k I e 2 ) + ^ d k e 1
+
+z
(2) (e(2)+^
+ z k , к + 1 \ e 2 + d k e 1 /J+
+ 2 ( 1 + a 3, к + 1 ) d k c k + 1 ^ d k [ e 22) ] +
+ l^ L(2)]2+le(2)e(2) +
+ 4 d k [e 1 J + 2 e 2 e 3 +
1 , (2) (2) , (2) ,2 (2) 1
+ -2- d k e 1 e 3 + e 1 d k e 2 r -
Уравнения (8), (11) и (12-14) позволяют по известным составляющим первого, третьего и пятого порядков малости параметров луча на входе в однородную среду вычислить соответствующие составляющие параметров луча на выходе из нее, то есть эти уравнения позволяют рассчитать ход псевдолуча пятого порядка через однородную среду, ограниченную двумя асферическими поверхностями оптической системы^ При этом каждая из этих поверхностей может представлять собой как поверхность оптического элемента, так и любую другую поверхность, например поверхность предмета или изобра-жения^
2. Расчет хода псевдолуча через дифракционные структуры, выполненные на асферической поверхности
Как уже отмечалось во введении, в работе [4] получены формулы расчета хода псевдолуча через ДЛ, структура которой выполнена на сферической поверхности^ Распространение этих формул на асферическую поверхность требует лишь получения выражений для величин различных порядков малости единичного вектора нормали k к этой поверхности в точке падения луча, определяемой вектором р •
Единичный вектор нормали к асферической поверхности можно найти, воспользовавшись выражением [5]:
k = V f/ V ( V F ) 2 • (15)
Подставив (3) в (15), получим, что составляющие вектора k ~ описываются соотношениями
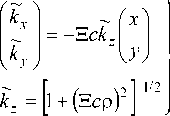
где
E = 1 -(с р)2 ] 12 +1 ^3 (c р)2 +
3 2(17)
+ 8 ^ 5 ( С р ) 4 + ... .
~ (2) =- 1 c 2 e (2)
z
~ (4) =- 1 c 2 e (4) + 2 e (2) e (2) ] + 3 c4 e (2) ] 2
z 23 3
Для того чтобы представить составляющие kx , ky и kz в виде сумм величин различных порядков малости, вновь используем один из трех инвариантов вращения
2 (2)(4)
eз = р = e3 + e3 +... , где e 32) =[р(1)]2, e 34) = 2р(1)-р(3).(19)
Подставляя (18) в (16) и (17), а затем, раскладывая радикалы в ряд, получим
E(2) = 1 (1 + ,3 )c 2 e32)E(4) = 2 (1 + ,3 )c 2 e34) ++ 3 (1 ., )c4 e32) ]2
Соотношения (21-23) совместно с соответствующими формулами работы [4] позволяют произвести расчет хода псевдолуча через ДЛ, структура которой размещена на асферической подложке.
где
~
к y 7
~ kx
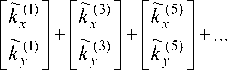
k z = 1 + k^ + k^ + ...
- c
—I
,
x (1)
y (1)
k x (1)
(1) ky
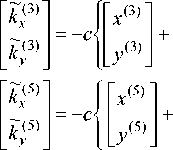
( e,2) + ~<2))
+ e (2) k^
x (1)
y (1)
(e(2) + ~(2))
x (3)
y (3)
+
+
(e141
+ ;)
x (1)
y (1)
, (21)


