Расчет и экспериментальное измерение спектров собственных колебаний ферритовых резонаторов невзаимных волноводных устройств СВЧ и КВЧ

В коротковолновой части СВЧ-диапазона особый интерес представляет собой излучение невзаимных устройств с высотой ферритового элемента, меньшей высоты волновода. Наличие воздушного зазора между ферритом и стенкой волновода приводит к возникновению неоднородности поля вдоль оси ферритового цилиндра, что значительно усложняет электродинамический анализ устройств. По этой причине в настоящее время, с одной стороны, отсутствует теория, достаточно хорошо описывающая экспериментальные дисперсионные характеристики ферритовых устройств в широком диапазоне частот. Существует лишь небольшое количество работ, в которых исследуется феррито-диэлектрические резонаторы с высотой, меньшей высоты волновода (см., например, [1]). С другой стороны, в последнее время в научно-технической литературе появились сообщения о разработке достаточно широкополосных циркуляторов, функционирующих на высших типах колебаний ферритовых резонаторов (резонаторов увеличенных размеров) в коротковолновой части СВЧ-диапазона. Например, в [2] говорится о создании циркулятора в полосе частот от 92,5 ГГц до 100,6 ГГц (к сожалению, в этой работе не определены геометрические размеры резонатора). Все это говорит о необходимости исследований спектров собственных колебаний намагниченных феррито-диэлектрических резонаторов, без знания которых невозможна оптимизация ферритовых устройств.

В данной работе приводятся и обсуждаются экспериментальные и теоретические результаты исследований спектра собственных колебаний ферритовых резонаторов с высотой феррита меньше размера волновода. В приближении магнитных стенок получено уравнение для определения собственных частот резонатора. Полученное соотношение является унифицированным. Оно справедливо как для Е-, так и для Н-плоскостных устройств. Кроме того, рассматриваются и вопросы оценки рабочей полосы частот ферритовых приборов.

• 1.    Математическая модель ферритового резонатора. Уравнение для определения собственных частот

В целях достаточно максимальной общности рассмотрим ферритовый резонатор с граничными условиями Ex = Ey = 0 при z = 0, H (на рис. 1, а показана его геометрия, H – высота резонатора). Так как ферритовый цилиндр намагничен вдоль своей оси (вдоль оси z ), то собственные колебания в структуре распадаются на две невзаимные группы, причем для одной группы колебаний в плоскости z = H 2 справедливо граничное условие Ex = Ey = 0 (электрическая стенка), а для другой - Hx = Ey = 0 (магнитная стенка). Очевидно, что в устройствах с ферритовым элементом, высота которого равна размеру волновода, возбуждаются колебания обоих типов. Если высота ферритового элемента меньше высоты волновода (рис. 1, б ),

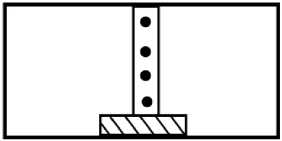
а

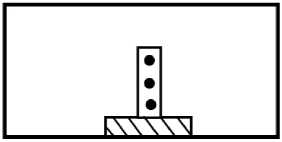
б

Рис. 1. Геометрия резонаторов: а – резонатор с высотой феррита, равной размеру узкой стенки волновода; б – резонатор с частичным заполнением феррита (высота феррита меньше размера волновода)

Fig. 1. The geometry of the resonators: a – a resonator with a ferrite height equal to the size of the narrow waveguide wall; b – a resonator with partial filling of ferrite (the height of the ferrite is less than the size of the waveguide)

ТГ ^E ^m E , ТГ H = —в т ^Н ,              (3)

дz 2               д z где вm = mл/И, число m = 0,1,2,3...

Для получения уравнения для определения собственных частот резонатора (рис. 1, а ) обратимся к модели резонатора с магнитными стенками H ф = Hz = 0 на боковой поверхности ферритового цилиндра [3] и воспользуемся выражениями для составляющих электромагнитного поля в гиро-тропной среде из монографии [4]. В результате нетрудно записать следующее уравнение:

Ф 1 1 П ( X R )( Y 2 - F₂ ^a 2 ) - I n ( Х ₂R )( Ф 1 У 1 -« 1 ) = 0,         (4)

где

a i = к б

( к ² БЦ-в ² m ) i n ( х 1 R ) + ^ I n ( х 1 R )

R

^Y i  ^в т

R ( k ² sn^-₽ m ) I n ( х i ^R ) + Ц a k 2 ^Б I n ( x i R ) ,

то при достаточно больших значениях диэлектрической проницаемости ^ ( ^> 10) и размерах зазора S между верхним основанием цилиндра и стенкой волновода, когда под влиянием верхней стенки волновода, можно пренебречь, на верхнем основании ферритового цилиндра можно положить граничное условие H _т = 0 [3]. Поэтому собственные колебания ферритового резонатора с неполным заполнением (рис. 1, б ) и ферритового резонатора, геометрия которого показана на рис. 1, а с дополнительным условием H _т = 0 при z = Я /2, совпадают. Таким образом, модель ферритового резонатора (рис. 1, а ) может быть использована при проектировании Н- и Е-плоскостных невзаимных устройств как с ферритовым элементом, высота которого меньше высоты волновода, так и с полным заполнением.

Гиротропный цилиндр (рис. 1, а ) будем характеризовать тензором магнитной проницаемости.

*     *               *     *                    *    *                    *     *              *    *

Ц = Цц x 0 x 0 + Ц y 0 y 0 + 1 Ц a y 0 z 0 ^- 1 Ц a y 0 z ₀ + Ц z ₀ z ₀,      (1)

где x 0 , y 0 , ^— 0 - единичные вектора декартовой системы координат. С учетом периодичности поля, т. е. сохранения значений для составляющих поля при изменении угла ф на 2 п можно принять, что поле

E , И - e^{in ф},                                              (2)

где число n = 0, ± 1, ± 2,...

Кроме того, из граничных условий Е _т = 0 при z = 0, H следует, что

1 n,             x .

^х 1,2 = 2 R ^ - ^{Ц 11)} -I ^{1 +}

2 m

±

±

1 k ²

Ф 1 =

F ₂ =

-

—

' ^б(ц1 ^-ц 11 ) -I ¹

Ц a ^{k Бв} m

—

2 ' m

^Ц a

^{+ в} m ^k 2 ^БЦ 111 —

Ц

,

,

Ц 11 ² _ ² I ^в m ^х 1 I

^Ц         У

Ц a ^k Ц 11 ^в m

^ц ( k 2 ^Бц 1 -_P m -^х 2 )

Ц ± =Ц

^^^^^^

^Ц a

,

^Ц д

I n ( х i ^R ) = — I n ( х i p ) при P = ^R ,

I n ( x ) - функции Бесселя первого рода, к = 2 п f/c -волновое число.

д

Рассмотрим частные случаи. При — = 0 (m = 0) д z уравнение (4) принимает вид

I n ( ^kR Т^бЦ 1 ) + ^5^ I n ( ^kR 7^бЦ 1 ) = 0.

При предельном переходе к изотропному случаю ( ц a ^ 0, Ци ^ ц ) из уравнения (4) следует простая формула:

R = х ni

- 1

,

где х _ni - i корень уравнения i n ( x ) = 0.

Очевидно, что спектр собственных колебаний намагниченного феррита тесно связан со спек-

Физика волновых процессов и радиотехнические системы. 2020. Т. 23. № 1. С. 39–44

Physics of Wave Processes and Radio Systems, 2020, vol. 23, no. 1, pp.

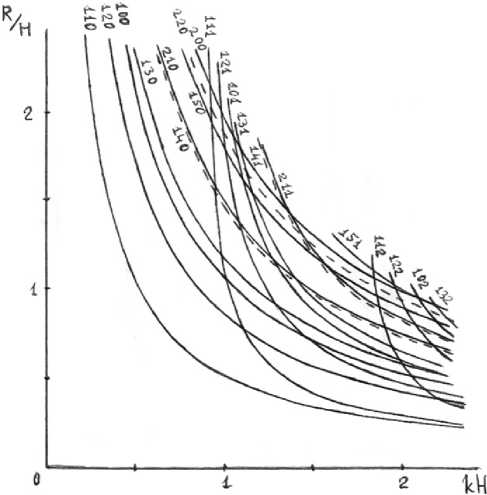
Рис. 2. Спектр собственных колебаний ненамагниченного ферритового резонатора ( ^ = 12,5 )

Fig. 2. The spectrum of natural vibrations of a non-magnetized ferrite resonator ( £ = 12,5 )

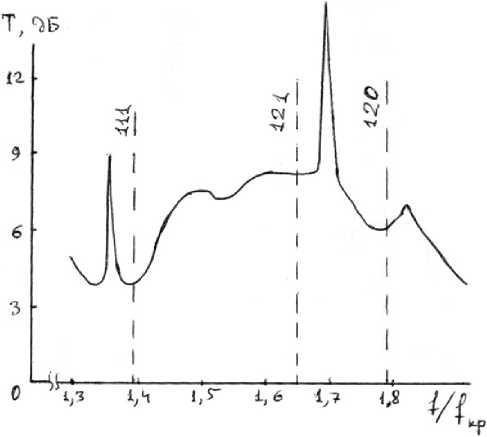
Рис. 3. Спектр коэффициента прохождения Т ненамагниченного ферритового цилиндра в Y-разветвлении волноводов b / a = 0,5; R = 0,31 b

Fig. 3. The transmission coefficient spectrum T of a non-magne-tized ferrite cylinder in the Y-branch of the waveguides b / a = 0,5; R = 0,31 b

тром ненамагниченного резонатора. Поэтому прежде всего рассмотрим основные закономерности спектра колебаний ненамагниченного резонатора.

Будем классифицировать собственные колебательные структуры (рис. 1, а ) тремя целыми числами ( i , n , m ), где i ( i = 1, 2, 3, ...) - характеризует вариацию поля вдоль координаты р , n ( n = 0, ± 1, ± 2, ± 3, ...) определяет вариация поля вдоль координаты ф , а параметр m ( m = 0, 1, 2, 3, ...) - число вариаций поля вдоль оси z .

На рис. 2 представлены результаты расчета спектра собственных колебаний ненамагниченного ферритового резонатора с ^ = 12,5. Представленные зависимости RH от величины kH имеют универсальный характер и несут большое количество информации. Действительно, эти результаты могут быть использованы как при проектировании Н-плоскостных устройств (R^H < 1,5), так и при конструировании Е-плоскостных устройств ( R/h > 1,5). Знание спектра собственных колебаний резонатора позволяет и более четко представить физические аспекты работы невзаимных ферритовых устройств. Тем более что в литературе принцип работы волновых циркуляторов, как правило, объясняется с помощью одного колебания. Из рис. 2 следует, что при определенных размерах R, H в рабочей полосе устройства может возникнуть сразу несколько колебаний, в том числе и нежеланных. Картина спектра собственных колебаний резонатора принципиально меняется и изменением величины RH. Знание спектра собственных колебаний резонатора позволяет принять специальные меры к устранению нежелательных колебаний и тем самым улучшить электродинамические параметры устройства.

2.    Н-плоскостной циркулятор.Экспериментальные результаты

На рис. 3 показана экспериментальная зависимость коэффициента прохождения Т для одного из плеч симметричного Y-разветвления в Н-плоскости с ненамагниченным ферритовым цилиндром, высота которого равна высоте узкой стенки волновода. Здесь же нанесены и собственные колебания ферритового резонатора, рассчитанные нами и попадающие в исследуемый частотный диапазон. В качестве резонатора использовался цилиндр из феррита 1СЧ4, диаметр феррита - 0,31 а , высота - H = b , где а , b - размеры широкой и узкой стенок прямоугольного волновода. На рис. 4 представлены экспериментальные зависимости Y-циркулятора с ненамагниченным ферритом, расположенным на металлическом согласующем трансформаторе, при различных значениях зазора S . Из рис. 4 следует, что спектр собственных колебаний резонансной системы в исследуемой частотной области существенно зависит от величины зазора S . Появление даже очень малых зазоров ( S « H ) существенно изменяет ча-

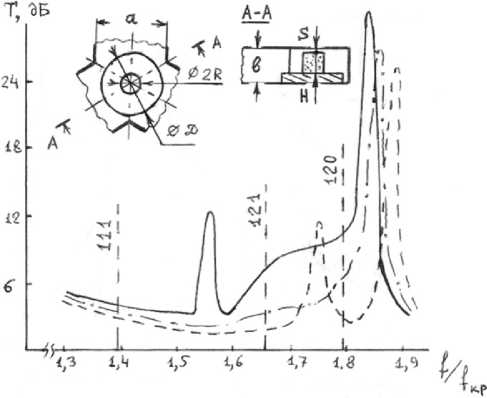
Рис. 4. Спектр коэффициента прохождения Т Y-циркулятора с ненамагниченным ферритом, расположенным на металлическом согласующем трансформаторе, при различных значениях зазора S / b : S / b = 0 - сплошная кривая; S / b = 0,008 - пунктирная кривая; S / b = 0,022 - штрихпунктирная кривая

Fig. 4. The spectrum of the transmission coefficient T of a Y-circulator with non-magnetized ferrite located on a metal matching transformer, at various clearance values S / b: S / b = 0 - solid curve; S / b = 0,008 - puncternal curve; S /b = 0,022 - dash-dot curve стотные свойства Н-плоскостного развлетвления с ферритовым разветвлением.

Резонансный характер экспериментальных зависимостей говорит о возбуждении собственных колебаний резонатора волной H 1Q в данном интервале частот. Из рис. 4 также видно, что вблизи резонаторов существуют области, в которых не-намагниченный ферритовый резонатор не оказывает влияния на коэффициент прохождения. На центральных частотах этих областей модуль коэффициента прохождения | т | ® 2^3 (4 дБ) [1].

При приложении внешнего магнитного поля взаимность устройства нарушается, что приводит к неравенству коэффициентов прохождения по плечам. Частотные зависимости, соответствующие этому случаю, приведены на рис. 5, из которого следует, что при определенном значении подмагничивающего поля существуют области невзаимности. На этом же рисунке показаны и собственные частоты f innm намагниченного резонатора, определенные с помощью уравнения (4) (верхний знак «+» соответствует величине +ц a в соотношении (1), а знак «-» - величине -ц a ). При этом наблюдаются следующие основные закономерности. Во-первых, частотная зависимость коэффициента прохождения Т в одном из возможных направлений практически сохраняется, уменьшается лишь абсолютное значение коэффициента (в 2-3 раза). В обратном направлении на-

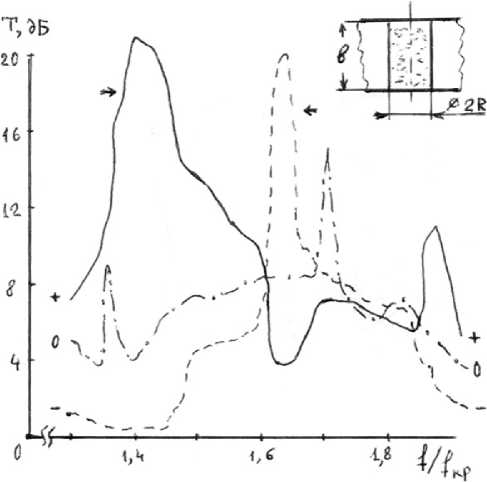
Рис. 5. Частотная зависимость коэффициента Е для намагниченного (+, –) и размагниченного (0) феррита

Fig. 5. Frequency dependence of the coefficient E for magnetized (+, –) and demagnetized (0) ferrite блюдается значительное смещение резонансных частот ферритового резонатора. Интересно отметить и тот факт, что максимальная величина развязок циркулятора достигается в области, где в отсутствие магнитного поля коэффициент прохождения Т имеет наименьшее значение. Аналогичные закономерности наблюдались в работе [1]. Во-вторых, рабочая полоса устройства определяется разностью (fПт - fnm), и она, по-видимому, не может превышать величины (f1 - f2), где f1? f2 -соседние частоты ненамагниченного ферритового резонатора.

3.    Е-плоскостной циркулятор. Экспериментальные результаты

На рис. 6, 7 представлены экспериментальные результаты исследований Е-плоскостного циркулятора: на рис. 6 – зависимость коэффициента прохождения Т для одного из плеч разветвления с ненамагниченным ферритовым элементом; на рис. 7 - частотные зависимости коэффициента прохождения для намагниченного ферритового резонатора. На этих рисунках нанесены и собственные частоты ненамагниченного резонатора, попадающие в данный интервал частот. В качестве резонатора использовался феррит 1СЧ4 (4 лц 0 = 4700 Гс, ^ = 12,5). Диаметр феррита составлял 0,57 a , высота 0,28 a . Основное отличие характеристик Е-плоскостного устройства от соответствующих зависимостей Н-плоскостных

Физика волновых процессов и радиотехнические системы. 2020. Т. 23. № 1. С. 39–44

Physics of Wave Processes and Radio Systems, 2020, vol. 23, no. 1, pp. 39–44

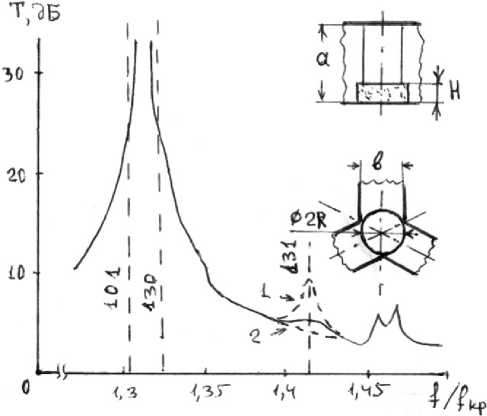
Рис. 6. Зависимость коэффициента прохождения Е для одного из плеч Е-плоскостного циркулятора с ненамагниченным ферритовым элементом (пунктирные кривые 1, 2 соответствуют двум направлениям остаточной намагниченности)

Fig. 6. The dependence of the transmission coefficient E for one of the arms of the E-plane circulator with a non-magnetized ferrite element (dashed curves 1, 2 correspond to two directions of the residual magnetization)

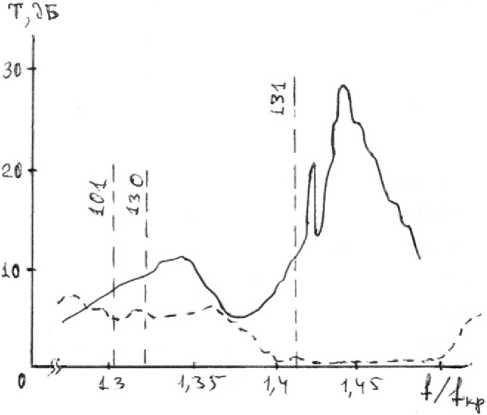
Рис.7. Частотные зависимости коэффициента прохождения Т для намагниченного ферритового резонатора. При прохождении электромагнитных волн в двух противоположных направлениях

Fig. 7. Frequency dependences of the transmission coefficient T for a magnetized ferrite resonator. When passing electromagnetic waves in two opposite directions

приборов определяется типами возбуждаемых колебаний в ферритовых резонаторах. Полученные нами экспериментальные и теоретические результаты хорошо согласуются и с экспериментальными результатами работы [5].

Заключение

Резонаторная модель невзаимных приборов СВЧ позволила с единых позиций подойти к проектированию Е- и Н-плоскостных устройств. Выявленные основные закономерности спектра собственных колебаний ферритовых резонаторов позволяют определить и оптимальную процедуру настройки невзаимного ферритового прибора. Она должна состоять из следующих основных моментов.

• 1.    Излучение частотных свойств устройства с не-намагниченным ферритом. Определение областей циркуляции, оценка максимальной возможной рабочей полосы частот, выбор геометрии резонатора.

• 2.    Изучение частотных свойств устройства с намагниченным ферритом. Выбор оптимальной величины магнитного поля.

На основе результатов, полученных выше, можно проектировать вентили, циркуляторы и фильтры на подмагниченных ферритовых резонаторах.