Расчет и оптимизация параметров измерительных узлов автоматизированных систем контроля

Противоречие между постоянно растущими требованиями к чувствительности измерительных средств и линейности их выходных характеристик традиционно решается применением активных электронных приборов: операционных усилителей, компараторов и т. д. Как правило, это приводит к снижению параметрической устойчивости измерительных устройств и автоматизированных систем контроля (АСК), в целом, частью которых они являются.1

В настоящее время актуальной является задача выбора оптимальных параметров элементов схем по заданным требованиям к ее характеристикам, включая и требования по стабильности. В частном случае – оптимизация параметров измерительных узлов автоматизированных систем контроля (АСК) и контрольно-проверочной аппаратуры (КПА) различных объектов контроля (ОК), для которых характерны измерения в области сверхмалых то- ков и напряжений. К таким контролируемым параметрам относятся:

• •    сопротивления изоляции цепей питания;

• •    сопротивления нагрузки;

• •    качество соединения цепи «корпус».

Использование в таких измерителях пассивных элементов (резисторов) значительно повышает параметрическую устойчивость измерительных устройств и АСК в целом, но, с другой стороны, в связи с уменьшением значений измеряемых параметров предъявляет повышенные требования к выбору значений резисторов измерительных цепей и методам обработки результатов измерений.2

Перечисленные выше требования приводят к необходимости решения задачи оптимального параметрического синтеза, состоящей в выборе значений параметров измерительной системы, обеспечивающих максимальную точность измерения контролируемого сигнала.

Решение этой проблемы позволяет повысить точность и сократить сроки создания первых образцов систем контроля за счет уменьшения времени, необходимого для их отладки и настройки.

Рассмотрим задачу оптимального параметрического синтеза, состоящую в выборе оптимальных значений параметров хопт (х1опт, . , хп опт) ^ Dx измерительной системы, обеспечивающих максимальную точность измерения контролируемого сигнала, рассчитываемого по формуле у/ = F/(ивх, х1, ., хп), в заданном диапазоне его изменения

а/ < у/(х) < b/, 1 = 1 ...т, где Dx - область допустимых вариаций значений параметров; ивх - входной сигнал; х = {х,}П — вектор параметров системы; у = {У/}™ - вектор выходных контролируемых параметров системы; F - известный оператор, зависящий от топологии измерительной системы; а = ymin - минимальное значение контролируемого параметра; b = утах -максимальное значение контролируемого параметра. Причем область допустимых вариаций значений параметров Dx, как правило, неизвестна.

Приведенная выше задача может быть решена графическим или аналитическим методом на основе уравнений чувствительности. Рассмотрим метод анализа параметрической чувствительности и стабильности применительно к измерительным схемам.

Параметрическая чувствительность - зависимость динамических свойств системы от вариации её параметров и характеристик. Под вариацией параметров понимают любые отклонения их от значений, принятых за исходные. Эти отклонения могут быть известны полностью и описаны некоторыми функциями или же известны только с точностью до принадлежности к определенному классу (например, ограничены по модулю). Вариации параметров могут быть конечные или бесконечно малые, при этом порядок дифференциального уравнения, описывающего их, может оставаться неизменным или изменяться. В качестве прямых оценок чувствительности принято использовать так называемые функции чувствительности, играющие большую роль в количественной оценке степени влияния вариаций параметров системы на её динамического свойства.

Необходимость учета параметрической чувствительности при решении задач оптимизации параметров обусловлена различными причинами.

Во-первых, часто оптимальный режим находится в области высокой параметрической чувствительности. Это может привести к тому, что неизбежные небольшие изменения входных воздействий существенно повлияют на результирующую величину контролируемого сигнала. В этом случае целесообразно находить такой оптимальный режим, при котором учитывается чувствительность измерительной системы по каждому входному сигналу в определенном диапазоне его изменения.

Во-вторых, при оптимизации параметров приходится использовать математические модели измерительных узлов, в которые входят параметры, найденные с определенной степенью точности.

В таких случаях приходится идти на компро- мисс между оптимальностью и чувствительностью. Параметры должны выбираться так, чтобы критерий оптимальности не достигал экстремального значения, но зато был менее чувствительным к некоторым переменным. Практически здесь при- ходится решать задачу оптимизации по многим параметрам или задачу полиоптимизации.

Для расчетов будем использовать относительные функции чувствительности. Это безразмерные величины, позволяющие сопоставлять и оценивать влияние различных параметров и входных воздействий на выходные контролируемые параметры системы и на критерий оптимизации в любой точ- ке поиска.

Относительные функции чувствительности имеют следующий вид:

пУ; = дУ1 . “вх  пУг = Эу;, XJ

“ ^вх     ЭМ вх У_г ' ^Xj dx j у_; .

Исследуемое уравнение представим в виде обратной зависимости

Ubx = ЛУ/,ху).

На основании приведенных выше выражений параметрической чувствительности задача выбора оптимальных значений параметров хопт измерительной системы может быть сформулирована следующим образом: определить такие значения хопт, при которых удовлетворяются следующие условия:

• -    максимальной чувствительности функции и_вх(У / ) относительно каждого выходного контролируемого параметра у_; (максимально допустимый наклон графика функции и_вх(у_;):

max(S“BX), или max (А“°уУг));

• -    ограничение на линейность функции и_вх(у / ) -минимально возможное отклонение и_вх(у_;) от теоретической прямой, проходящей через точки а и b, соответствующие границам диапазона измерения,

min(AS“BX) , где AS“bx = П“х - П“вх, или

ГГ         Э“пхСУ7) - TZ                                         7

^ min <      * < ^ тах при условии Я < У / < Ь.

^эу ;

Рассмотрим подробнее применение аналитического метода для выбора оптимальных парамет- ров схем измерения сопротивлений изоляции це- пей питания Rизол.стат, Rизол.дин и нагрузки Rнагр.

Для измерения величины Rизол.стат предлагает- ся схема измерения, показанная на рис. 1.

Как видно из рис. 1, Rизол.стат определяется

формулой п изол.стат

й¹-Л2-Л и _ЗМ

Е^-Л2 —(Й1+Й2)-Л_изм ,

где R 1 и R 2 - эталонные сопротивления, величина

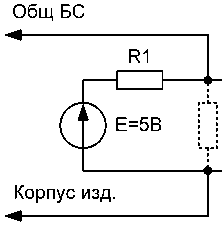
Рис. 1. Схема измерения R изол.стат резистивным способом

на АЦП МК (0В-5В)

которых определяется в зависимости от диапазона изменения величин R _{изол.стат} .

Определим чувствительности выходного напряжения схемы измерения сопротивления изоляции к входному контролируемому значению R изол.стат , а также ее параметрам R 1, R 2. Для этого запишем функцию в более удобном виде U изм =

⁼ f ( R изол.стат ,

^ изм

R 1, R 2):

^R изол.стaт '

. -R2-E

R1•R2+R _И зо _Л .стaт •(R1+R2)

и найдем частные производные функции и_изм _ 7 (R изол.стaт , R1, R2):

^^ изм Х^ изол.стат Д¹^²). _

E^R22

^9R изол.стaт

(R1•R2+R изол.стaт •(R1+R2))^2;

⁹U изм (.^R изол.стaт ,^R1,^R2'⁾    ^Д изол.стат Д^.^^^ДД изол.стат )..

dR1

^ ^ изм (^R изол.стaт ,^R1,^R2) __

9R2

(R1•R2+R изол.стaт •(R1+R2))² ;

________ ^E•^R1•^R изол.стaт _________

(R1•R2+R изол.стaт •(R1+R2))² .

Найдем выражения, описывающие относительные функции чувствительности по каждому исследуемому параметру измерительной схемы, согласно формулам (1):

5 ^ изм

^R изол.стaт

С и изм ⁵ R1

R1R

с ^ изм _

5R2 _

" R1•R2+R изол.стaт •(R1+R2)^;

^R1•^R2+^R1•^R изол.стaт   .

R1•R2+R изол.стaт •(R1+R2)^;

^R1•^R изол.стaт

В результате подстановки различных наборов значений сопротивлений R1,R2 максимальная относительная чувствительность схемы измерения к контролируемому значению Rизол.стaт составила 5.::стат _ 0,53 в начальной точке диапазона при а _ RH3OJiCTaT _ 300 кОм и 5^изм   _ 0,18 в конеч- изол-с1ат                         Rизол.стaт ной точке диапазона при b _ Rизол.стaт _ 1,5 МОм. Следовательно, R1 _ 500 кОм, R2 _ 1 МОм являются оптимальными величинами для заданного диапазона измерения.

Также с помощью разницы относительных чувствительностей в граничных точках диапазона измерения Д5 ^ ^изм   _ 5 ^ ^изм _ 5 ^ ^изм можно опре-

^R изол.стaт        ^          ^

делить максимальную линейность схемы измерения. Применительно к схеме измерения сопротивления изоляции она составляет Д5 У ^изм   _ 0,34

R изол. стат при R1 _ 500 кОм, R2 _ 1 МОм.

Рассмотрим результаты расчета и_изм на основе графического метода, проведенные с использованием интегрированной математической системы Mathcad 11.0а в соответствии со схемой, представленной на рис. 1.

Как видно из полученных зависимостей U изм = f ( R изол.стат ), приведенных на рис. 2, наилучшие результаты (в соответствии с условием сформулированной задачи) для диапазона измерения

R1•R2+R изол.стaт •(R1+R2) .

< 1,5 МОм могут быть полу-

0,3 МОм < R изол.стат

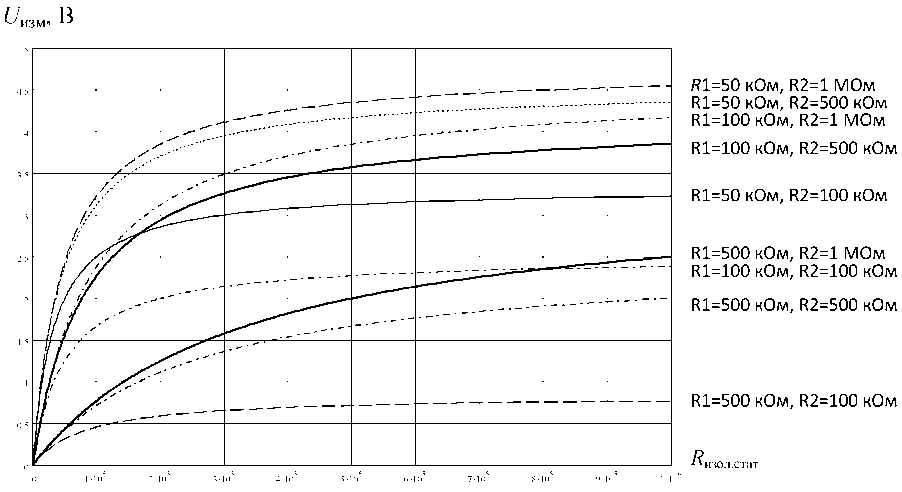
Рис. 2. Результаты расчета U изм = f ( R изол.стат ) для R 1 = 0,05 МОм, 0,1 МОм, 0,5 МОм; R 2 = 0,1 МОм, 0,5 МОм, 1 МОм

на АЦП МК (0В-5В)

на АЦП МК (0В-5В)

Рис. 3. Схема измерения R изол.дин

чены при следующих значениях: R 1 = 0,5 МОм, R 2 = 1 МОм.

В этом случае Δ U изм составляет 1 В в заданном диапазоне изменения R изол.стат . Также следует отметить, что при этих значениях R 1 и R 2 достигается и высокая линейность U изм = f ( R изол.стат ), что обеспечивает погрешность измерений U изм менее 5 %.

Таким образом, результаты графического и

аналитического методов полностью совпали.

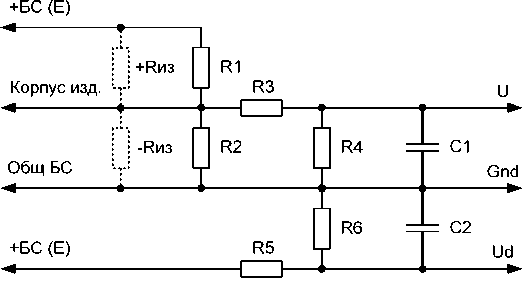
Схема измерения ±R изол.дин , характеризующая

величину сопротивления изоляции между цепями питания (±27 В) и корпусом контролируемого изделия в процессе проведения контроля объекта, показана на рис. 3.

Данная схема целесообразна для измерения ±R изол.дин при работе с высокоомными цепями кон-

троля.

Расчет ±R изол.дин может быть проведен по фор-

мулам:

R^ =

1                                 _

R4 / Е-(К1+й+ _з ) 1 ! 1 \ Rl+Диз 1L ;

R3+R4 V Rl-й+з Уизм⁺«3 ^ Rl-й+з R2 R3

при 0 < ^изм < ир;

где

R

+ _ из

R U3 -R1-R2-( U u3m -(R3+R4)-E-R4)

Q

при Uu3M > Up

Q — R—з • R2 • R4 • E - иизм • [R1 • R2 • (R3 + R4) + +R-3 • ((R1 + R2) • (R3 + R4) + R1 • R2)];

U —         R2-R4-E p   R2-(R3+R4)+R1-(R2+R3+R4);

U — E-

R6

R5+R6 .

Решение указанной задачи может быть получено аналитическим методом, а также по графикам U изм = f ( ±R изол.дин ), рассчитанным для различных значений R 1 –R 6. Указанные графики приведены на рис. 4–6.

Как показали расчеты, параметры выходных значений U изм слабо зависят от резисторов R 2, R 5, R 6, что позволяет не анализировать графики указанных зависимостей при различных значениях R 2, R 5, R 6.

С целью решения задачи оптимизации расчет

зависимости U _изм = f ( ±R _{изол.дин}) проводился для различных значений R 1 и R 3 (см. рис. 4), R 4.

Как видно из приведенных на графиках зависимостей U изм = f ( ±R изол.дин ), оптимальными значениями параметров схемы (см. рис. 3) являются R 1 = 1 МОм, R 3 = 1,4 МОм, R 4 = 280 кОм.

При низкоомном значении сопротивления контролируемых цепей схема, представленная на рис. 3 преобразуется в схему рис. 1.

Наиболее просто решается задача измерения R нагр , для которой характерна классическая схема измерения, показанная на рис. 5.

В данном случае расчетной формулой является

D _ Rl-^изм

R™rp — E—иизм, где R1 – эталонное сопротивление.

Проведем аналогичный анализ R _нагр для решения задачи в соответствии со схемой, представленной на рис. 5.

Результаты расчета U изм = f ( R нагр ), для диапазона изменения 20 Ом < R нагр <  200 Ом приведены на рис. 6.

Как видно из полученных зависимостей U изм = f ( R нагр ), наилучшие результаты (в соответствии с условием задачи) для диапазона измерения 20 Ом < R нагр <  200 Ом могут быть получены при значении R 1 = 300 Ом. В этом случае Δ U изм составляет 1,75 В в заданном диапазоне изменения R _нагр, при этом максимальная погрешность, определяемая нелинейностью выходной характеристики, составляет менее 6 %.

При проведении расчетов входное сопротивление измерителей не учитывалось.

Экспериментальная отработка параметров измерительных узлов АСК проводилась на макете, разработанном на основе микроконтроллера 1887ВЕ1У со встроенным 8-канальным десятиразрядным аналого-цифровым преобразователем (АЦП). Применение микроконтроллера со встроенным АЦП с программно задаваемым коэффициентом усиления входного сигнала обеспечило возможность автоматического изменения диапазона измерения (в отличие от схем на активных элементах), а также позволило разделить задачу контроля на задачу измерения аналогового сигнала и задачу

б)

а)

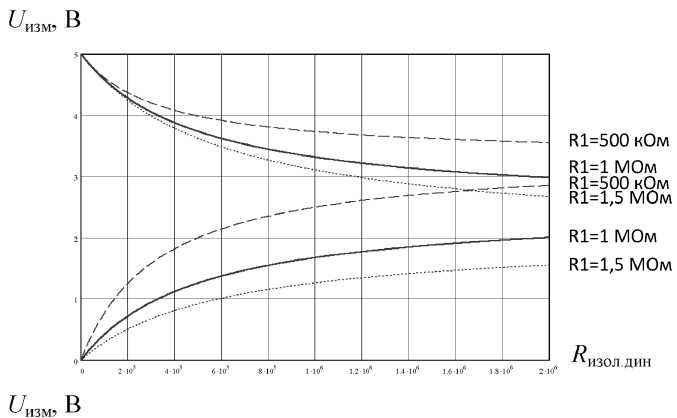
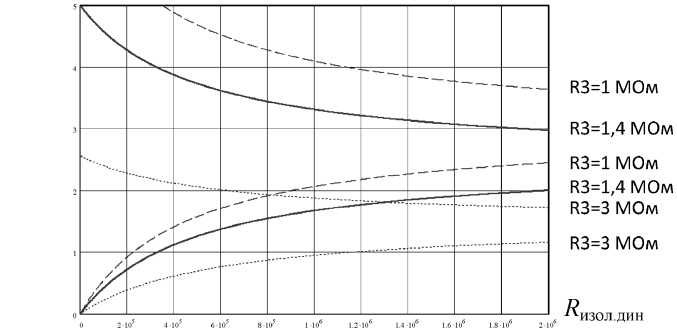
Рис. 4. Зависимость U изм = f ( ±R изол.дин ): а – при R 2=2,43 МОм, R 3=1,4 МОм, R 4=280 кОм, R 5=19,6 кОм, R 6=2,8 кОм; б – при R1 =1 МОм, R2 =2,43 МОм, R 4=280 кОм, R 5=19,6 кОм, R 6=2,8 кОм

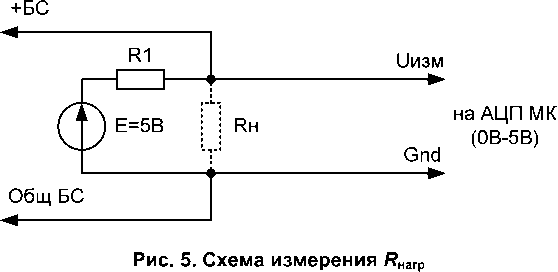
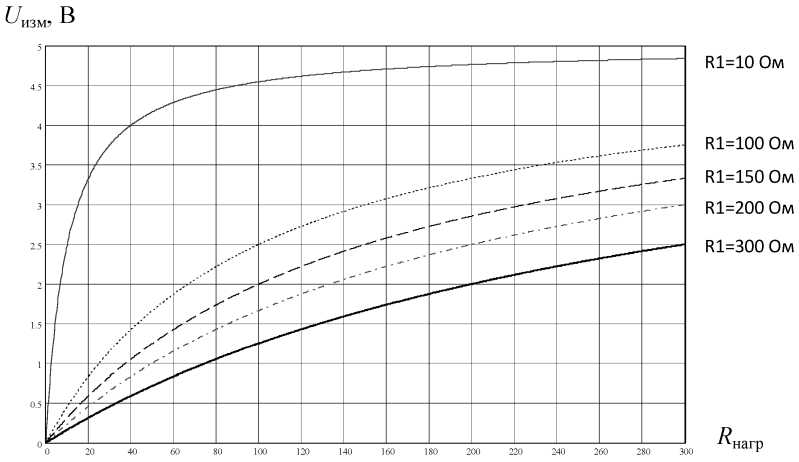
Рис. 6. Результаты расчета U изм = f ( R нагр ) для диапазона изменения 20 Ом < R нагр <  200 Ом

цифровой фильтрации полученных результатов по известным алгоритмам непосредственно в измерительном устройстве. В итоге данные особенности привели к увеличению параметрической устойчивости автоматизированных систем контроля в целом, за счет исключения влияния помех в измеряемых цепях, а также к сокращению сроков создания первых образцов АСК.

Оценка правильности выбора параметров узла измерения Rизол.стат проводилась по 7 значениям сопротивлений в соответствии с формулой (2) при значении R1 = 500 кОм, R2 = 1 МОм, определен- ных по расчетным кривым (см. рис. 2).

Как видно из приведенных выше графиков (рис. 7), максимальная погрешность измерения значения R изол.стат составляет не более 4 %.

На рис. 8 приведены результаты эксперимента по измерению ±R изол.дин для 7 точек в диапазоне от 28 кОм до 1,4 МОм, при этом следует отметить, что погрешности измерений для приведенного диапазона практически отсутствуют, т.е. экспериментальные ±R изол.дин совпадают с расчетными значениями. Расчет ±R изол.дин проводился в соответствии с формулой (3).

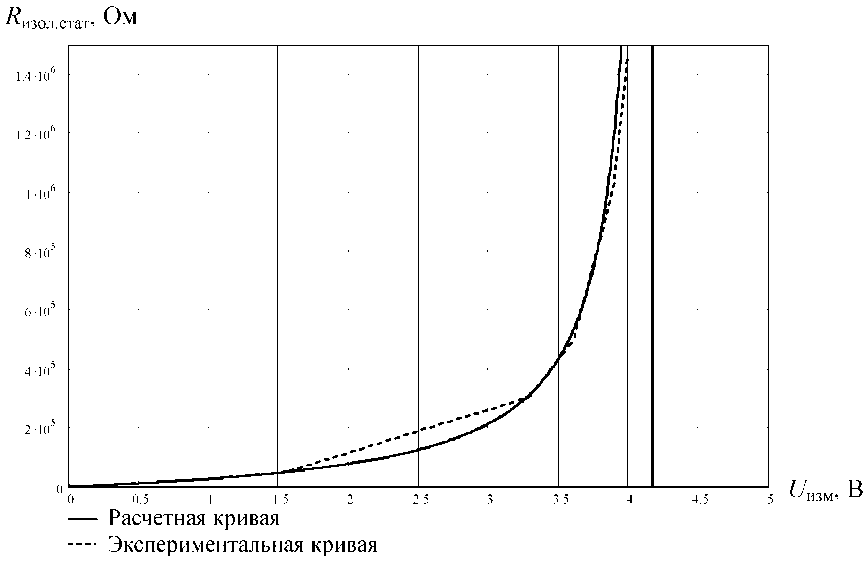
Рис. 7. Экспериментальная кривая измерения R изол.стат

^ИЗОЛ.ДИН, Ом

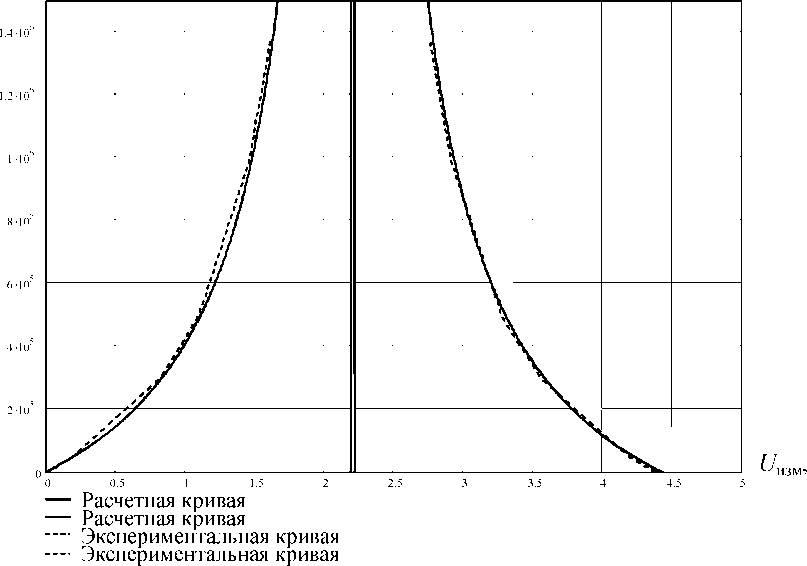
Рис. 8. Экспериментальная кривая измерения R изол.дин

Полученные в ходе проведенных экспериментов результаты позволили применить предложенные методы оптимизации параметров измерительных узлов и схемотехнические решения в разработке автоматизированных систем контроля электрических параметров различных систем управления.