Расчет и визуализация матриц упругих параметров эмали и дентина

Актуальность

Известно, что эмаль и дентин можно рассматривать как микронеоднородную гетерофазную среду [5]. Эмаль зуба образована эмалевыми призмами, которые состоят по преимуществу из плотно упакованных гексагональных кристаллов гидроксиапатита Са 10 (РО 4 ) 6 (ОН) 2 (НАР). Несмотря на разновидности, дентин представляет собой биокомпозит и состоит приблизительно на 45–70% из неорганического материала в форме кристаллитов минеральных веществ, в основном апатитов. Кристаллиты расположены между коллагеновыми волокнами и по классу симметрии относятся к гексагональной сингонии. Упругие свойства эмали и дентина как кристаллических субстанций, отнесенных к гексагональной симметрии, являются анизотропными и полностью определяются матрицами упругих постоянных c ij и коэффициентов податливости s ij . Компоненты матриц известны из литературных данных [9].

Отметим, что данные матрицы являются весьма разреженными, потому что только 12 из 36 элементов отличны от нуля (в противном случае, когда большинство элементов матрицы являются ненулевыми, матрица носит название плотной). При этом в матрицах только по пять элементов из ненулевых являются независимыми [4]. Для эмали – это с11 = 115,00, с12 = 42,40, с13 = 30,00, с33 = 125,00, с44 = 22,80 (ГПа); s11 = 0,0104, s12 = –0,0034, s13 = –0,0017, s33 = 0,0088, s44 = 0,0439 ГПа–1, для дентина – с11 = 37,00, с12 = 16,60, с13 = 8,70, с33 = 39,00, с44 = 5,70 ГПа; s11 = 0,0346, s12 = –0,0145, s13 = –0,0045, s33 = 0,0276, s44 = 0,1754 ГПа–1. Остальные элементы матриц c66 = (c11 – c12)/2 и s66 = 2(s11 – s12) соответственно или равны нулю.

В итоге матрицы, например, упругих постоянных эмали и дентина могут быть представлены в следующем виде:

	Эмаль					Дентин
115	42,4	30	0	0	0	37	16,6	8,7	0	0	0
42,4	115	30	0	0	0	16,6	37	8,7	0	0	0
30	30	125	0	0	0	8,7	8,7	39	0	0	0
0	0	0	22,8	0	0	0	0	0	5,7	0	0
0	0	0	0	22,8	0	0	0	0	0	5,7	0
0	0	0	0	0	36,3	0	0	0	0	0	10,2

Знание упругих постоянных матриц весьма информативно и позволяет рассчитать упругие модули Юнга и сдвига, объемный модуль, коэффициент Пуассона, а также другие упругие характеристики поликристаллических материалов, каковыми являются реальные твердые ткани зуба. Визуализация разреженных матриц нередко позволяет выявить не только любопытные, но и полезные свойства математических закономерностей, которые порождают такие матрицы или описываются последними. Часто необходимо знать, где расположены ненулевые элементы, т.е. получить так называемый шаблон матрицы.

Цели и задачи. Изучить анизотропию упругих свойств твердых тканей зуба путем их визуализации с помощью расчетно-графического пакета ELATE и пакета прикладных программ MATLAB на основе массивов упругих постоянных и коэффициентов податливости эмали и дентина.

Материалы и методы

Расчетно-графический пакет ELATE – Elastic tensor analysis – позволяет визуализировать матрицы c ij и s ij , что делает наглядными свойства упругой анизотропии материалов. Инструкцию по работе с данной оболочкой можно найти в работе [6], а сама она представлена на http://progs.coudert.name/elate. В распоряжении исследователей предусмотрены следующие интерактивные функции: поворот графиков вокруг двух осей, добавление на график линий каркаса, возвращение к нулевым настройкам, экспорт графика в графический онлайн-редактор https://plot.ly и сохранение графика в виде изображения.

Пакет прикладных программ MATLAB https://matlab.ru имеет специальные средства для визуализации разреженных матриц, реализованные рядом команд. Наглядную информацию о соотношении величин элементов матрицы дает функция imagesc, которая интерпретирует матрицу как прямоугольное изображение. Каждый элемент матрицы представляется в виде небольшого квадрата, цвет которого соответствует величине элемента. Для того чтобы узнать соответствие цвета и величины элемента, следует использовать команду colorbar, выводящую рядом с изображением матрицы шкалу цвета.

Результаты исследования

Результаты, полученные с помощью графической части программы ELATE , можно видеть на рис. 1–3. Условно в данном пакете поверхность, представляющая g (ф,0) = max_v X (ф,0,ф), где X = E, G , ц, отображается полупрозрачным голубым цветом, тогда как для f (ф, 0) = min_v X (ф, 0, ф) применяется зеленый цвет.

E

Эмаль

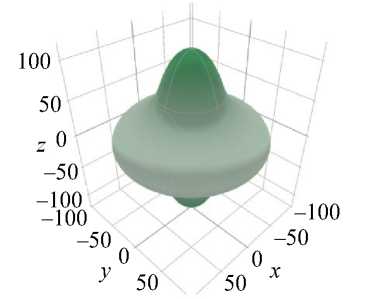
Дентин

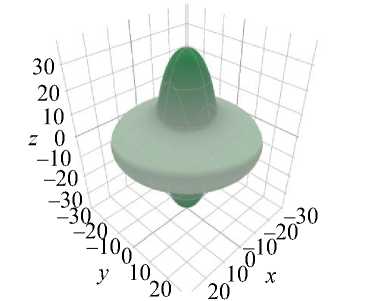
G

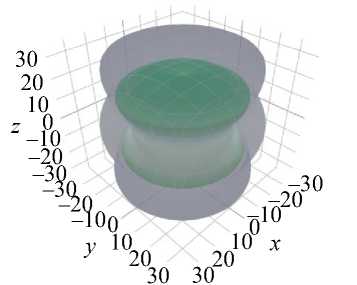
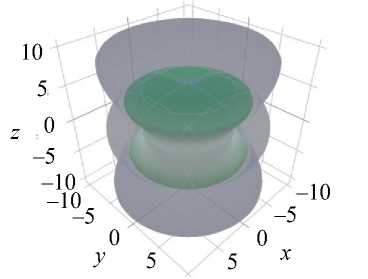
µ

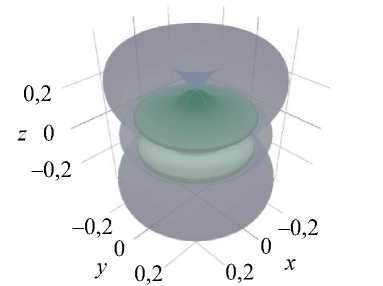
Рис. 1. 3 D -диаграммы упругих модулей E и G и коэффициента Пуассона µ эмали и дентина, полученные с помощью пакета ELATE

µ

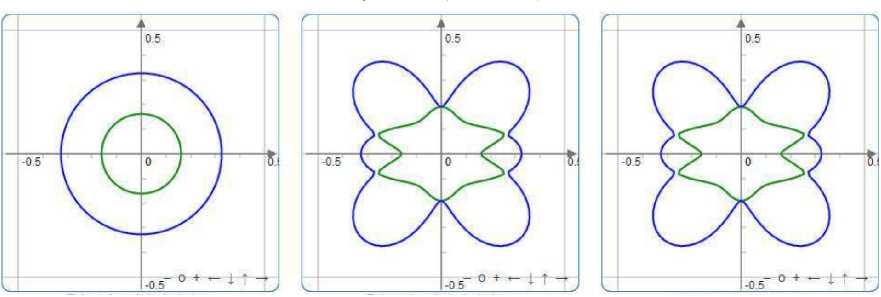
Коэффициент Пуассона (плоскость yz )

Коэффициент Пуассона (плоскость xy )

Коэффициент Пуассона (плоскость xz )

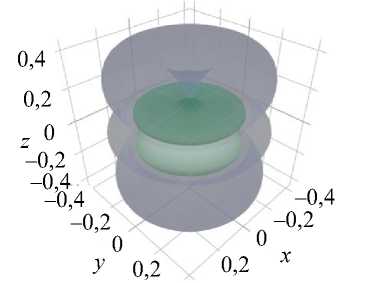
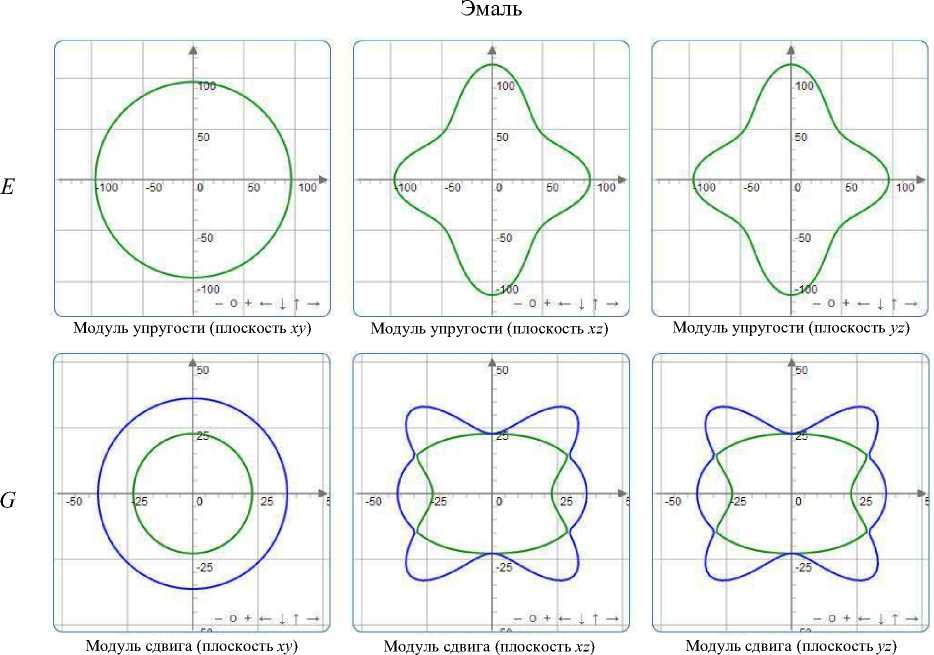
Рис. 2. Диаграммы упругих модулей E и G и коэффициента Пуассона µ эмали, полученные с помощью пакета ELATE

На графиках видно, что и эмаль, и дентин обладают ярко выраженной анизотропией упругих свойств и сильной ориентационной зависимостью всех параметров упругости – упругих модулей и коэффициента Пуассона. Полученные ориентационные зависимости при этом весьма схожи попарно, что, очевидно, связано с принадлежностью минеральной фазы эмали и дентина к одной (гексагональной) сингонии. Тем не менее, масштаб диаграмм упругих модулей эмали и дентина существенно различается по величине, что согласуется с известными экспериментальными данными, полученными на макрообразцах твердых тканей интактных зубов, согласно которым уровень упругих свойств эмали выше, чем у дентина.

Кроме того, пакет ELATE позволяет рассчитать ряд физических параметров твердых тканей зуба.

Таблица 1

Способ усреднения	Объемный модуль, ГПа	Модуль Юнга, ГПа	Модуль сдвига, ГПа	Коээфициент Пуассона
Voigt	K V = 62,2	E V = 84,599	G V = 33,22	µ V = 0,27331
Reuss	K R = 62,196	E R = 78,744	G R = 30,545	µ R = 0,28899
Hill	K H = 62,198	E H = 81,689	G H = 31,882	µ H = 0,2811

Таблица 2

Собственные значения матрицы упругих постоянных эмали

λ 1	λ 2	λ 3	λ 4	λ 5	λ 6
22,8 ГПа	22,8 ГПа	36,3 ГПа	72,6 ГПа	95,786 ГПа	186,61 ГПа

Таблица 3

Вариации упругих модулей эмали

Параметр	Модуль Юнга, ГПа		Линейная сжимаемость, ТПа –1		Модуль сдвига, ГПа		Коээфициент Пуассона
	E min	E max	β min	β max	G min	G max	µ min	µ max
Величина	66,88	113,56	5,3147	5,449	22,8	44,354	0,1593	0,47035
Анизотропия	1,698		1,0253		1,945		2,9525
Направляющие косинусы
Ось	0,6855 0,2591 0,6804	0,0000 0,0000 1,0000	0,2588 0,9659 0,0000	0,0000 0,0000 1,0000	0,0000 0,0000 1,0000	–0.4023 0,5815 –0,7071	0,4112 0,3403 0,8456	0,3282 0,5995 –0,7300
Вторая ось	–	–	–	–	–0,7660 0,6428 –0,0000	0,4024 –0,5815 –0,7071	–0,6375 0,7704 0,0000	–0,3506 –0,6403 –0,6835

Здесь упругие характеристики G и µ определяются ориентацией двух связанных между собой ортогональных векторов, задающих плоскость и направление сдвига в первом случае, и направления продольной и поперечной деформации во втором (другими словами, двумя осями).

Известно, в предположении, что ориентация зерен в поликристалле равновероятна и поликристалл, как любое изотропное тело, характеризуется двумя упругими константами, задача об определении эффективных упругих свойств была решена сначала Фойгтом [11] путем усреднения матрицы упругих модулей кристалла, а затем Ройсом [10] из усреднения матрицы коэффициентов податливости. Более детальное рассмотрение, выполненное Хиллом [7], показало, что эти усреднения соответствуют предположениям об однородности деформаций в поликристалле в первом случае и однородности напряжений – во втором, а получаемые значения объемного модуля и модуля сдвига поликристалла дают верхнюю и нижнюю вариационные границы для его эффективных свойств. Им же было предложено определять эффективные упругие характеристики как среднее арифметическое значений, получаемых в приближениях Фойгта и Ройса [2]. Данные, представленные в табл. 1 и 4, с высокой степенью точности подтверждают выводы Хилла.

Обращает на себя внимание, что наибольшую упругую анизотропию демонстрируют значения коэффициентов Пуассона эмали и дентина (2,95 и 3,78) соответственно, а наименьшую – коэффициенты линейной сжимаемости (1,03 и 1,19), при этом коэффициенты анизотропии упругих свойств, вычисленные для модулей Юнга и сдвига, близки между собой как у эмали (1,70 и 1,95), так и у дентина (2,07 и 2,46) (табл. 3 и 6).

Таблица 4

Усредненные технические механические характеристики дентина

Способ усреднения	Объемный модуль, ГПа	Модуль Юнга, ГПа	Модуль сдвига, ГПа	Коээфициент Пуассона
Voigt	K V = 20,111	E V = 24,817	G V = 9,5867	µ V = 0,29434
Reuss	K R = 20,031	E R = 21,664	G R = 8,2077	µ R = 0,31975
Hill	K H = 20,071	E H = 23,255	G H = 8,8972	µ H = 0,30689

Таблица 5

Собственные значения матрицы упругих постоянных дентина

Вариации упругих модулей дентина

_ cl i + c i2 + 2 c зз

¹              6 c ₄₄

—

4r c13

, A2

c ll - c i2

—

A3 = Al A2, A4 = s33, s11

2 5 13 + s 33

.

s ₁₁ + s ₁₂ + s ₁₃

λ 1	λ 2	λ 3	λ 4	λ 5	λ 6
5,7 ГПа	5,7 ГПа	10,2 ГПа	20,4 ГПа	31,994 ГПа	60,606 ГПа

Таблица 6

Параметр	Модуль Юнга, ГПа		Линейная сжимаемость, ТПа –1		Модуль сдвига, ГПа		Коээфициент Пуассона
	E min	E max	β min	β max	G min	G max	µ min	µ max
Величина	17,457	36,176	15,626	18,669	5,7	14,048	0.14176	0,53564
Анизотропия	2,072		1,1947		2,465		3,7784
Направляющие косинусы
Ось	0,7302 0,0000 0,6832	0,0000 0,0000 1,0000	1,0000 0,0001 –0,0000	0,0000 0,0000 1,0000	0,0000 0,0000 1,0000	0,5291 0,4691 –0,7071	–0,1845 0,4025 –0,8966	0,6795 0,0001 –0,7337
Вторая ось			—		–0,7660 0,6428 –0,0000	–0,5291 –0,4692 –0,7071	–0,9091 –0,4167 0,0000	–0,7337 –0,0001 –0,6795

Здесь A1, A2 и A3 – отношения жесткостей на растяжение-сжатие к модулям сдвига. Для кристалла, упругоизотропного по отношению к деформации, все три показателя анизотропии равны единице. A4 – полезный показатель анизотропии упругой деформации при растяжении получен из отношения модулей Юнга в направлениях, перпендикулярном и параллельном оси шестого порядка. A5 – наглядный показатель анизотропии деформации при всестороннем сжатии.

При подстановке в данные формулы численных значений упругих постоянных c ij и коэффициентов податливости s ij эмали и дентина получим A 1 = 2,83, A 2 = 0,56, A 3 = 1,58, A 4 = 0,80, A 5 = 1,19, что по порядку величины может ассоциироваться с данными табл. 3 и 6 для анизотропии упругих модулей твердых тканей зуба.

Нельзя не отметить аномально высокое значение коэффициента Пуассона дентина, что выше теоретического предела коэффициентов Пуассона для поликристаллических изотропных материалов, каковыми, например, являются стоматологические композитные соединения. Заметим, что отсутствие идентичности физических свойств дентина и пломбировочных материалов может негативно сказываться на качестве реставраций. Максимальное значение коэффициента Пуассона дентина 0,53–0,54 больше максимального значения коэффициента Пуассона эмали 0,47, что не противоречит исследованиям химического состава твердых тканей зуба, согласно которым содержание воды в эмали зубов 1–4%, дентина – до 10%, эти показатели соотносятся с тем, что вода, являющаяся жидкостью, практически несжимаема и имеет высокий коэффициент Пуассона (до 0,5).

С высокой точностью и без рутинных вычислений пакет ELATE позволяет определить собственные значения матриц упругих постоянных (табл. 2 и 5) и направляющие косинусы экстремальных значений упругих свойств (табл. 3 и 6). Для последних несложно проверить, что соответствующие суммы квадратов направляющих косинусов равны во всех случаях единице.

Мы также сверили данные в табл. 6 для коэффициента Пуассона дентина с расчетами в пакете компьютерной алгебры MATHCAD . Для одного из коэффициентов Пуассона (µ 31 (ψ, θ)) гексагональной решетки применили формулу

Ц 31 ( У , 0 ) =

sin² у sin² 0 cos² 0 ( s _n + s ₃₃ - s ₄₄) + (cos² 0- sin² 0 cos 2 0 sin² y ) s ₁₃ + sin² 0 cos² у s₁₂

s ₃₃

где s ₃₃ = cos 0 s ₃₃ + sin 0 cos 0 (2 s ₁₃ + s ₄₄) + sin 0 s j у и 0 - углы Эйлера.

Формула дает отношение Пуассона для продольного удлинения вдоль Ox ^' и поперечного сжатия вдоль Ox ^' .

Стандартная процедура MATHCAD для нахождения максимума функции двух переменных дала идентичные с табл. 6 результаты:

• 4    := 1     9 := 0.5

0.5 < 9 < 1

Given

0 < 4* < 3 14

Zj 571\       cos(1.571) -* -0.ОО02036732О369522583254

Maximize(p.31,4 ,9) =   " ' 1       cos(0.747) -* 0.73373048948907736602

<0-747 J V 7                    05

^31(1.571,0.747) = 0.536              ',1 - cos(1.571) - cos(0.747) f -^ 0.67944059881003948248

Аналогичную картину наблюдали для µ 32 (ψ, θ) дентина и коэффициентов Пуассона эмали.

Возможность визуализации матриц с помощью специализированного пакета MATLAB в градациях серого цвета представлена на рис. 4. На полученных диаграммах видно, что уровень упругих свойств эмали существенно выше, чем у дентина, что не противоречит опытным данным, согласно которым в норме модуль Юнга эмали у взрослых пациентов E = 75…90 ГПа, а модуль Юнга дентина около E = 10…20 ГПа

[1, 8]. Кроме того, палитра оттенков серого на диаграммах подобна друг другу, что подтверждается литературными данными, согласно которым упругая изотропия эмали и изотропия дентина отличаются друг от друга незначительно.

Из рис. 4 следует, что среди всех упругих постоянных наибольшее значение имеют элементы матриц c 11 как у эмали, так и у дентина. Помимо того что эта постоянная входит в соответствующее выражение для закона Гука кристаллов, она сама по себе не имеет прямого физического смысла, поэтому этот факт нами специально не изучался.

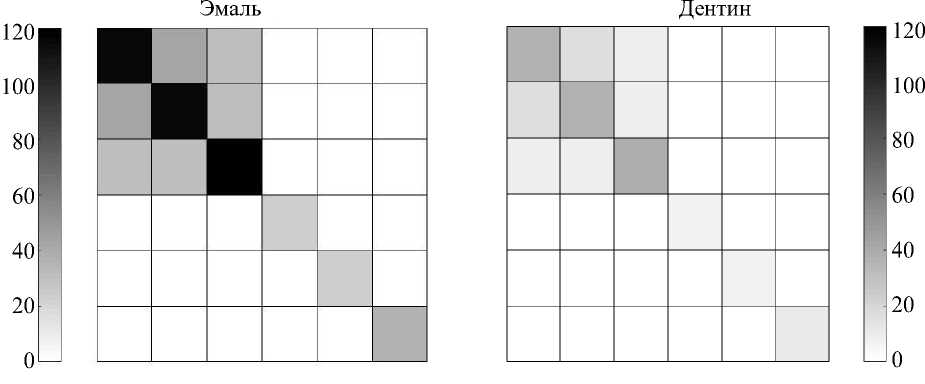
Рис. 4. Визуализация матриц упругих постоянных эмали и дентина в пакете прикладных программ MATLAB (градации серого)

Более строгий анализ упругой анизотропии эмали и дентина как минеральноорганического комплекса и микронеоднородной гетерофазной системы возможен с привлечением достижений теории анизотропных сред с кристаллографической текстурой. Несмотря на то, что все призмы минеральных веществ в эмали и дентине обладают одинаковым кристаллическим строением, они отличаются взаимной ориентацией кристаллографических осей и ходом призм. В центральной части каждой призмы кристаллы лежат почти параллельно ее длинной оси; чем больше они удалены от этой оси, тем значительнее отклоняются от ее направления, образуя с ней все больший угол («ёлочкой»). Полное исследование должно быть основано на знании пространственного распределения кристаллографических осей отдельных призм эмали и кристаллов апатитов дентина.

Выводы

Получено наглядное подтверждение факта упругой анизотропии твердых тканей зуба, обусловленной кристаллической структурой их минеральной составляющей (гидроксиапатитов). Наивысшую упругую анизотропию демонстрируют значения коэффициентов Пуассона эмали и дентина, наименьшую – коэффициенты линейной сжимаемости, при этом коэффициенты анизотропии упругих свойств, вычисленные для модулей Юнга и сдвига, близки между собой как у эмали, так и у дентина. Изучение и визуализация показателей упругих свойств и упругой анизотропии эмали и дентина имеет практическое значение при изучении проблем прочности твердых тканей зуба и качества стоматологических реставраций.

Благодарности

Работа выполнена в соответствии с планом НИР AAAA-A16-116102010059-6 Федерального государственного автономного научного учреждения «Центр информационных технологий и систем органов исполнительной власти» (2017–2021 гг.) кафедры нормальной физиологии и медицинской физики Московского государственного медико-стоматологического университета имени А.И. Евдокимова, а также при поддержке гранта РФФИ № 18-01-00589 и при финансовой поддержке Правительства Пермского края (грант на развитие научной школы Пермского края «Компьютерная биомеханика и цифровые технологии в биомедицине»).