Расчет эффективности управления проводимостью графена действием электрического поля в терагерцовом диапазоне частот

Практическая демонстрация возможности отделения и стабильного существования графена, продемонстрированная в 2004 году [1], стала настоящим прорывом в исследовании углеродных материалов. Графен представляя собой монослой атомов углерода, объединенных в гексагональную решетку (рис. 1). Расстояние между ближайшими атомами углерода в графене составляет около 0,14 нм. Кристаллическая решетка графена представляет собой плоскость, состоящую из шестиугольных ячеек, то есть является 2D-гексагональной кристаллической решеткой [2]. В элементарной ячейке кристалла находятся два атома.

Графен является одной из форм углерода (рис. 2). Наиболее распространенные методы получения образцов графена можно разделить на четыре категории: микромеханическое отщепление от объемного пиролитического графита, химический метод с использованием коллоидных дисперсий на основе соединений, содержащих графеновые слои, эпитаксиальный рост на поверхности различных монокристаллических подложек и термическое разложение SiC, хими- ческое разложение из газовой фазы на поликри-сталлических подложках (никель, медь) [1].

В качестве материала графен является совершенно новым – не только самым тонким, но и самым прочным. Как проводник электричества он идентичен меди и превосходит все другие известные материалы по теплопроводности [3]. Удельное электрическое сопротивление этого материала при комнатной температуре равно ~ 1 мкОм ■ см, что на 35 % меньше, чем у меди [4]. По прочности на разрыв он превосходит сталь в 200 раз, а масса слоя графена толщиной в один атом размером 60 на 120 метров составляет менее 1 г.

Графен обладает уникальными физическими, электронными и оптическими свойствами в широком диапазоне частот от радиочастот, микроволн до оптического диапазона. Графен способен управлять излучением терагерцового (ТГц) и ближнего инфракрасного диапазонов.

Целью данной работы является расчет поверхностной проводимости монослоя графена, определяемой формулой Кубо, в модели, учитывающей внутри- и межзонную проводимости, при различных значениях химического потенциала, изменяющегося при приложении внеш-

Рис. 1. Монослой графена, изображение получено с помощью электронного микроскопа высокого разрешения [2]

Рис. 2. Слои графена на кремниевой подложке (изображение с электронного микроскопа с увеличением 5000 раз) [4]

него электрического поля, в терагерцовом (ТГц) диапазоне частот.

• 1.    Физическая модель

Уникальные свойства графена обусловлены его кристаллической и электронной структурами. Графен нельзя отнести ни к металлам, ни к полупроводникам, ни тем более к диэлектрикам. В отличие от металлов, у которых зависимость энергии квазичастиц от импульса при движении в зоне проводимости (закон дисперсии) можно считать квадратичным (энергия квазичастиц прямо пропорциональна квадрату импульса), у графена закон дисперсии существенно отличается. Графен – это полуметалл.

Кристаллическая структура графена состоит из двух эквивалентных подрешеток, что приводит к образованию двух энергетических зон и двух «конических» точек на уровне нулевого заряда носителей К и К’, в которых валентная зона и зона проводимости соприкасаются (рис. 3) [4].

Исходя из зонной структуры (рис. 3), графен – это вещество, у которого валентная зона и зона проводимости перекрываются (запрещенная зона отсутствует как в металлах), но в отличие от металлов это пересечение очень мало. Точки соприкосновения зоны проводимости и валентной зоны в графене образуют так называемые

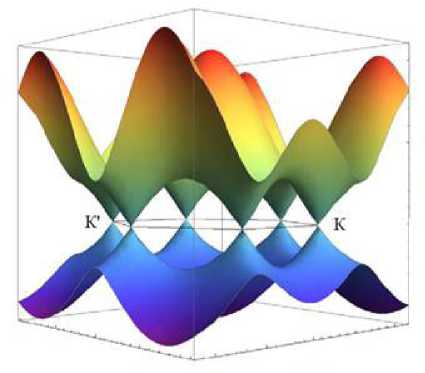
Рис. 3. Зонная структура графена с точками соприкосновения зоны проводимости и валентной зоны в точках К и К’ [5]

точки Дирака. В этих точках закон дисперсии квазичастиц имеет линейный вид: энергия квазичастиц прямо пропорциональна их импульсу. Подобной зависимостью энергии от импульса обладают еще и безмассовые частицы – фотоны, т. е. электроны в графене ведут себя как фотоны, имея нулевую массу и скорость движения vF порядка 10⁶ м/с, соответствующую энергии Ферми. В графене при положительных энергиях (выше дираковской точки) токонесущие состояния подобны электронам и заряжены отрицательно [6]. При отрицательных энергиях, если валентная зона целиком не заполнена, квазичастицы ведут себя как положительно заряженные частицы (дырки) и могут рассматриваться как твердотельный аналог позитронов [7].

Нулевая масса носителей заряда графена обусловливает их исключительно высокую подвижность – параметр, характеризующий пригодность материала для применения в электронике. Согласно измерениям А. Гейма и К. Новоселова, предельное значение подвижности носителей заряда в этом материале при комнатной температуре и плотности носителей 10¹² см ^{- 2} составляет 20 м² / В ⋅ с (для сравнения – подвижность носителей заряда в кремнии составляет 0,15 м² /В ⋅ с). При повышении температуры подвижность падает [4].

На подвижность электронов и дырок в графене существенное влияние оказывают примеси в диэлектрике подложки SiO2 (рис. 2). Подложка кремния с диэлектриком, на котором находится графен, должна быть сильно легирована, чтобы ее можно было использовать в качестве обратного затвора [1], при помощи которого можно управлять концентрацией и даже изменять тип проводимости. Поскольку графен является полуметаллом, то приложение положительного напряжения к затвору приводит к электронной проводимости графена, и напротив – если приложить отрицательное напряжение, то основными носителями станут дырки, поэтому в принципе нельзя обеднить полностью графен от носителей.

Высокая подвижность носителей заряда в графене делает его перспективным материалом для использования в различных приложениях, в частности, как будущую основу наноэлектроники и возможную замену кремния в интегральных микросхемах, и способствует созданию электронных приборов и устройств ТГц- и ИК-диапазонов.

2. Математическая модель

Монослой графена характеризуется поверх-

ностной проводимостью ст _s , определяемой формулой Кубо [8]:

ст _s ( to , ц c ) =

- ie ² k_hT —у, —— ^х n H 2 ( to - i 2 Г )

( х —— + 2 ln exp

I kbT      I

-ц c kbT

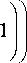
ie ² ( to- i 2 Г ) П Й 2

^

J

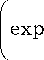
(-^ - цc

I k b T

-

/

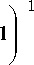
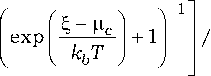
( to - i 2 Г )²

-

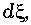
где e = 1,6 ■ 10 ¹⁹ Кл — заряд электрона; k b = 1,38 ■ 10 ²³ Дж/Кл — постоянная Больцмана; Й = 1,054 ■ 10 ^{- 34} Дж ■ с — постоянная Планка; T — температура; Г — частота релаксации; ц — химический потенциал; to = 2 п f — круговая частота. Поверхностная проводимость ст s графена является комплексной величиной с положительной действительной частью ст S . Мнимая часть поверхностной проводимости ст " содержит отрицательный вклад от внутризонной проводимости и положительный – от межзонной.

В задачах электродинамики используется эффективная диэлектрическая проницаемость графена, в уравнения Максвелла входит объемная удельная проводимость ст , которую необходимо

выразить через поверхностную проводимость ст _s . Для монослоя графена вводится комплексная

диэлектрическая проницаемость [8]:

i ст ( to , ц_с)

s ( to , ц c ) = 1 +------- f- ,                               (2)

soto d где d – эффективная толщина монослоя графена, а поверхностная стs и объемная ст проводимости связаны между собой соотношением: ст = ст s / d.

3. Результаты расчета проводимости графена при различных значениях химического потенциала в терагерцевом диапазоне частот

Расчет поверхностной проводимости графена проведен по формуле (1) для комнатной температуры T = 300 K. Приняты следующие значения параметров: частота релаксации Г = 10¹² 1/с, эффективная толщина слоя графена d = 1 ■ 10 м. Диапазон изменения химического потенциала ц _c = 0 - 1 эВ.

Зависимости поверхностной проводимости ст _s графена от частоты в широком интервале частот от 1 ГГц до 1000 ТГц, который включает СВЧ-, ТГц- и ИК-диапазоны, показаны на рис. 4.

Из рис. 4 видно, что в диапазоне частот от 0,001 ТГц до 0,1 ТГц действительная часть ст S проводимости графена является практически постоянной величиной.

На рис. 5 показаны расчетные зависимости действительной и мнимой частей комплексной диэлектрической проницаемости графена от частоты в ИК-диапазоне от 200 ТГц до 1000 ТГц при различных значениях химического потенциала.

Из графиков на рис. 5 следует, что при различных значениях химического потенциала действительная часть комплексной диэлектрической проницаемости меняет знак с «–» на «+» и стремится к единице. При этом мнимая часть диэлектрической проницаемости знака не меняет. На частотах до 0,1 ТГц графен ведет себя как металл. Начиная с частоты 2 ТГц и выше мнимой частью диэлектрической проницаемости графена можно пренебречь.

Проводимость графена в ТГц-диапазоне определяется, согласно модели (1), химическим потенциалом, который можно изменять, например, приложением внешнего электрического поля [8]. При изменении химического потенциала от 0 до 1 эВ поверхностная проводимость графена ст _s увеличивается почти в 20 раз (рис. 4). Изменение химического потенциала осущест-

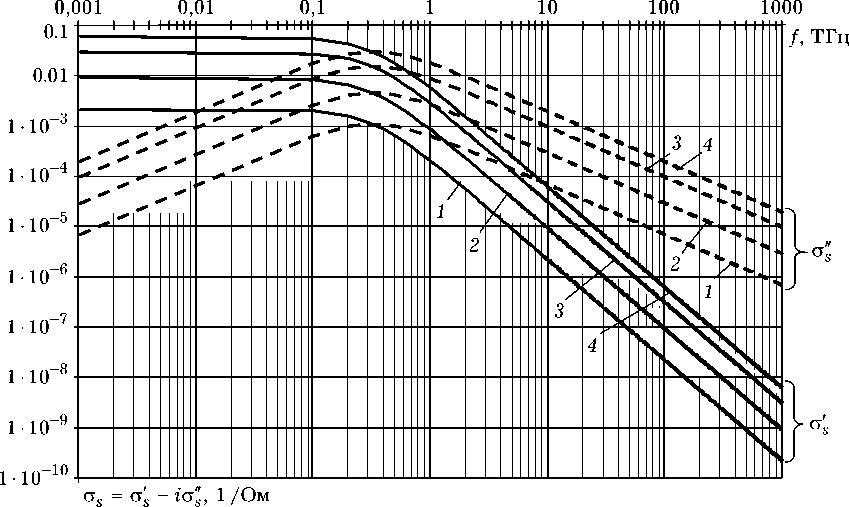
Рис. 4. Частотные зависимости действительной и мнимой частей поверхностной проводимости графена в СВЧ-, ТГц- и ИК-диапазонах при различных значениях химического потенциала: 1 — ц _с = 0,0 эВ, 2 — ц с = 0,15 эВ, 3 — ц с = 0,5 эВ, 4 — ц _с = 1,0 эВ

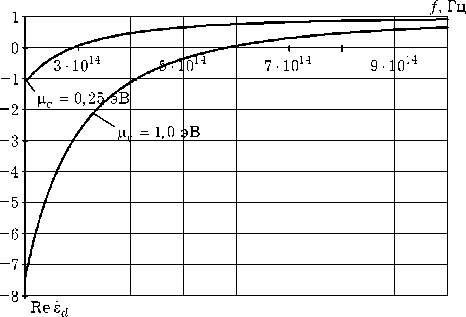
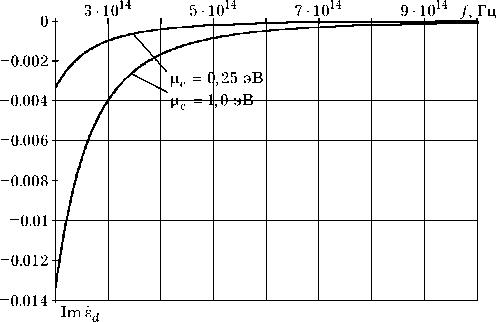
Рис. 5. Зависимости действительной и мнимой частей комплексной диэлектрической проницаемости графена от частоты в ИК-диапазоне при различных значениях химического потенциала

°s = MM^I)))

Графен

Рис. 6. Схема управления проводимостью графена при изменении химического потенциала приложенным внешним электрическим полем E ₀

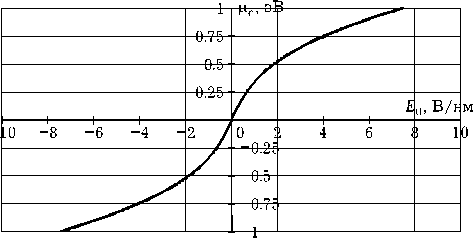
Рис. 7. Зависимость химического потенциала ц _с от напряженности внешнего постоянного электрического поля E ₀

вляется составляющей вектора напряженности внешнего электрического поля E ₀, нормальной к плоскости графена [9] (см. рис. 6). Для учета влияния зависимости химического потенциала ц _с от внешнего электрического поля Е о на поверхностную проводимость графена, нужно соответствующую зависимость ц _с ( E о) учесть в формуле (1).

Нормальная к плоскости графена составляющая вектора электрической индукции равна [10]

D o = б b Б о E 0 = en s /2, (3) где б ь — диэлектрическая проницаемость графена; n_s – 2D по в ерхно с тная плотность элек т рического заряда. Поверхностная плотность заряда n_s определяется выражением [10; 11]

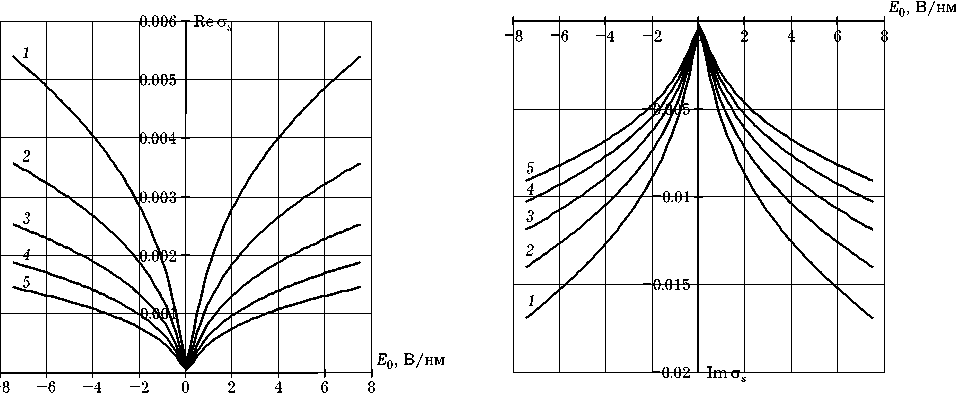
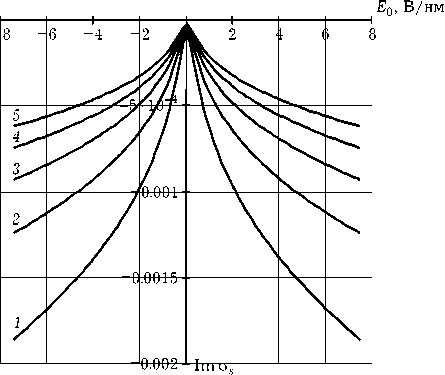
Рис. 8. Зависимость действительной и мнимой частей поверхностной проводимости графена от напряженности внешнего постоянного электрического поля E о : 1 — f = 1 ТГц, 2 — 1,25 ТГц, 3 — 1,5 ТГц, 4 — 1,75 ТГц, 5 — 2 ТГц

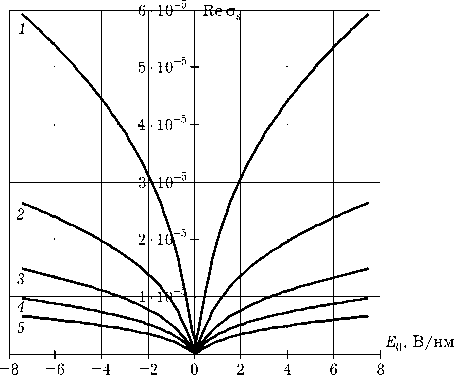
Рис. 9. Зависимость действительной и мнимой частей поверхностной проводимости графена от напряженности внешнего постоянного электрического поля E о : 1 — f = 10 ТГц, 2 — 15 ТГц, 3 — 20 ТГц, 4 — 25 ТГц, 5 — 30 ТГц

да ns = ГТ [ - (fd(-) - fd(- + 2цc)) d- ’           (4)

ПЙ2 VF о где

- 1

f ( б ) = exp -—— + 1

I I k b T J J

• — функция распределения Ферми-Дирака, - — энергия электрона, V f = 3 у о b / 2 й , где Y o = 2.7 эВ, расстояние между соседними атомами в структуре графена b = 0.142 нм. Из (3), (4) получаем выражение, связывающее между собой напряженность внешнего электрического поля E ₀ и химический потенциал ц c :

да

E 0 =  2Т   f ^S ( f d ^{( - )} - f d ^{( - +} 2 Ц c ) ) ^{d -} .          ⁽⁵⁾

л й ² v F ^- ь 0

Зависимость химического потенциала цc от напряженности внешнего постоянного электри- ческого поля E0, рассчитанная по формуле (5), показана на рис. 7.

Зависимости поверхностной проводимости графена от напряженности внешнего постоянного электрического поля E ₀, рассчитанные по формуле (3) с учетом (5), для различных частот ТГц диапазона приведены на рис. 8, 9.

Зависимости являются симметричными и нелинейными, особенно сильно нелинейность проявляется вблизи точки E 0 = 0.

Заключение

По формуле Кубо проведен расчет поверхностной проводимости монослоя графена и получены зависимости от частоты в широком интервале частот от 1 ГГц до 1000 ТГц, который включает СВЧ-, ТГц- и ИК-диапазоны. Показано, что на частотах до 0,1 ТГц графен ведет себя как металл, начиная с частоты 2 ТГц и выше мнимой частью диэлектрической проницаемости графена можно пренебречь.

Полученные в работе результаты демонстрируют, что управлять проводимостью графена можно путем изменения значений химического потенциала. При изменении химического потенциала от 0,0 эВ до 1,0 эВ поверхностная проводимость графена увеличивается примерно в 20 раз.

Управление химическим потенциалом осуществляется составляющей вектора напряженности электрического поля смещения, нормальной к плоскости графена. Показано, что зависимости поверхностной проводимости графена от напряженности внешнего постоянного электрического поля для различных частот ТГц-диапазона являются нелинейными.

Из результатов расчета следует, что графен, обладающий эффективно управляемой внешним электрическим полем проводимостью, чрезвычайно перспективен для создания широкого класса электронно-управляемых устройств ТГц-и ИК-диапазонов.

Работа поддержана Российским фондом фундаментальных исследований — грант № 12-02-97025-р_поволжье_а.