Расчет элементов тензора комплексной диэлектрической проницаемости для анизотропных материалов

В работе исследовался силицен – двумерный материал, аналог графена, имеет ряд предпочтительных отличий от него. В последнее время он и устройства на его основе довольно активно изучаются [3–6]. Пока нет отработанной технологии получения данного материала в силу его низкой стабильности [3]. Однако структурные, электрические и оптические свойства в силу их особенности продолжают исследоваться [7–9]. На рис. 1 представлена молекулярная структура силицена.

Цель данной работы – рассчитать недиагональные элементы тензора комплескной диэлектрической проницаемости пленки титана, используя подход Аграновича, Гинзбурга, изложенный в [1, с. 339]. Согласно этому подходу, компоненты тензора определяются по формуле:

численное решение уравнения Кона-Шэма для изолированного псевдоатома с теми же приближениями (обменный функционал, псевдопотенциал), что и для конденсированной системы.

1 d ²

2 r dr ²

l ( l + 1)

2 r ²

)

+ V ( r ) R ( r ) = ER ( r ).

Решение данного уравнения производится методом Нумерова.

Базисная функция представляется в виде:

Ф IImn ( r ) = R lln (| С Ь ^m ( Г I ).

s j ) ( to , k ) = 1

—

4п V ea s

”2 У ^'

ю2 V ^ m a

a

' a

ij

—

4n c ² у [ M nm HC M MC) A to 2 V m y n [ to ^— to m +to „

M^.. ( — k ) M n^ ( k ) ' to + to m — to n

Под n подразумевается основное состояние.

Для определения матричных элементов M mn ( Z c ) необходимо знать вид волновых функций.

Для их получения взята программа SIESTA, которая использует метод МО ЛКАО. В качестве базисных функций выбираются NAO (numerical atomic orbitals), которые представляют собой

Базис характеризуется размером (количеством функций на один атом), диапазоном (пространственным расширением орбиталей), формой радиальной части. В качестве радиальной части берутся гауссовы функции, в качестве угловой – функции Бесселя.

Интересно то, что базисные функции строятся для изолированных атомов, а используются в конденсированном веществе. Это делается для большей гибкости при описании различных систем.

Однако было решено использовать численные данные о базисных функциях, которыми оперирует SIESTA. В данной программе они представлены в виде

^ ц = У, ^C цv Ф v ,

V где c^ — коэффициенты при базисных волновых функциях фV , радиальная часть которой представлена таблично, а угловая аналитически.

Таким образом,

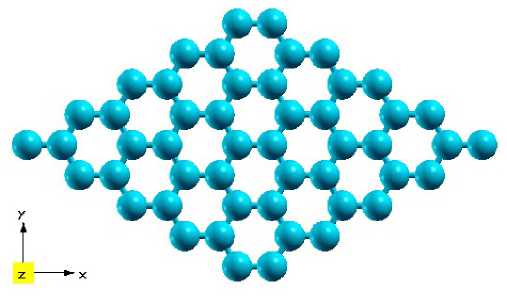
Рис. 1. Молекулярная структура силицена

—T„ „( r, 0, ф) = 5t m o(r, 8-ф)    + m0

д x _a                  д r _a     д x _a

дТ m o ( r , 0 , ф ) d0_a дТ m o ( r , 0 , ф ) дф а

.

^д0а    ^д x _a      дф а     ^д x a

Учитывая (1), преобразуем выражение выше:

д

-— У C цv R v ( r ) Y v ( 0 , Ф ) о x „

a

A

a y C цv R v ( r ) Y v ( 0 , Ф ) v ____________________ ^{d r} a +

Т.   У ^c ^v R V ( r ) Yv M.

V

a ^r a         a x a

Далее примем Т ц = Т n о — полная функция основного состояния системы.

Для расчета тензора диэлектрической проницаемости нужно знать компоненты матричных элементов М П _т ( к ) , которые находятся, исходя из того, что:

M nm ( к ) = <Т n 0 | М ( к )| Т m0} =

= IU T * n 0 М ( k ) Т m 0 dxdydz , xyz

M ( k ) = - У d^ ( p “ «" ■ + e ikr - p “ ) •

2 mc a ^a

~ a д p = - i n    .

'a

д У C av R v ( r ) Y v ( 0 , ф )

+    50a д0а        д xa

дУ Cav Rv (r) Yv (0, ф) v_______________дфа дфа       дxa

= У

v

+ У

v

+

' д ( C gv R v ( r ) Y v ( 0 , ф ) ) | д r _a ^         ^{д r} a         J ^д x a

" ^д ( ^c av ^R v ( ^r ) ^Y v ^{( 0}, ф)У| д0_а ^ ^д0_а        J ^д x a

+ У

v

"a( ^c av R v ( ^r ) Y v ( ⁰ ^ ⁾ ) ^ дф д

^д ф а

^{д x} a

Далее подставляем формулы выше в выражение для матричного элемента:

M nm ( k ) = j T n o ( r , 0 , ф ) x

V

= У l c цv Y v ( 0,ф ) v ^

^{д R} v ( ^r ) I ^{д r} a + ^{д r} a ) ^{д x} a

x

- У

2 mc a ^u

- i n A( e^ik ? « T m 0 ( r , 0 , _ф ) ) ₊ ^д r

У I ^c av ^R v ( ^r )

v ^

д Y v ( 0 , ф ) | д0 а а / x а

+ e^{ik ?} “

( - i n )^ T m 0 ( r , 0 , ф ) I dV . ^{д r} a              J

+ У 1 C av R v ( r ) v ^

д Y v ( 0 , ф ) J дф а дф_а J д x _а

.

Чтобы получить компоненты матричного элемента, необходимо умножить слева на единичный вектор:

a       d n p = - i n     .

x дx a

Тогда получаем:

M x ( k ) =- y mc ( p >“ - ^r-+ * - r- p a ) a ^a

Аналогично для M_n^y_m ( k ) и M_n^y_m ( k ).

Из формулы, определяющей матричный элемент видно, что для решения задачи нужно знать частные производные волновой функции по x , y , z .

Очевидно, необходимо найти производные T _m o ( r , 0, ф ) по пространственным координатам x , y , z . Ниже приведены результаты.

д r

— = sin 0 cos ф, д x д r

= cos 0 ;

д z д0 cos 0 cos ф

д r

— = sin 0 sin ф , д y

д x д0 д z дф д x

r

- sin 0

;

r

- sin ф r sin 0

дф д y

д0 cos 0 sin ф д y       r

cos ф r sin 0

^ 0.

д z

Выражения для компонент матричных элементов (на примере x -й) после взятия производ-

ных упрощаются:

_

M um ( k ) = J y „ о ( r , 0 , ф ) х

V

х

—Z

а

e (        (

——1^— i ^h I ^ik x ^e x “ ^Y m 0 ( ^r , ⁰ ф ) ⁺

2 m а c (   (

+ ^xr

a

^Y m 0 ( ^r , ⁰ Ф ) a ж а

—

— i h e^ik x r “

a

7-- ^Y m 0 ( ^r , ⁰ Ф )

^a x а

dV .

Данные интегралы берутся численно, методом трапеций [2], а производные – двухточечным методом. Должен быть учтен тот факт, что подынтегральные функции должны быть безразмерными. Размерность же производных волновой функции [ L ^{— 1}]. Также размерностью обладает элемент объема r ² sin 0 dr . Необходимо избавиться от размерности:

r = r0 r ‘, dV = d (V0 V'), где r] = 0.529E — 8.0 см (система СГС); r‘ - безразмерная величина.

Подставляя соответствующие переменные,

Раскрывая скобки, находим:

_

M Xm ( k ) = JX 0 ( r , 0 , Ф ) х

V

получаем:

_

M xm ( k ) =

Ne h

2 mc

х

-z

а

^e а

2 m _а c

^h k xe^{i k} x ^r “ W m 0 ( r , 0 ф ) ^—

_r r n 2 n

JJJ

— A o ( r , 0 , ф ) k x e^ikxr Y m o ( r , 0 , ф ) х

х r ²

— 2 i h e^ik x ^Xy m 0 ( r , 0 , ф ) a x а

dV .

r n 2n sin 0 dr d0 dф + JJ J 2ieikxrY^o(r, 0, ф) х

Далее для тождественных частиц (электронов) сумма под интегралом заменяется произведением:

a х — ax

Y _m о ( r , 0 , ф ) r ² sin 0 dr d 0 d ф ®

_

M^ xm ( k ) = JX o ( r , 0 , ф ) х

V

х

h k x e ik x r Y m о ( r , 0 , Ф ) —

— 2 i h e^ik x r ±Y m 0 ( r , 0 , ф )

dV ,

³ Г      nL m L

*  ---- h r h 0 h ф ^^^ q ijk ( ^—Y n 0 ( r ', ⁰ ф )

2 mcr0 L       ill jit k=l    V х kxekxr0r Ymo(r', 0, ф) r2 sin 0) + nm l

+ hrh0hф ZZ Z qijk 2ieikxr Yn0 (r', 0 ф) х i=1 j=1 k=1

a х^Y m 0(r, 0 ф) r 2sin 0 .

a x

где N – число электронов в единице объема.

Вынося константы за знак интеграла и опуская проекции, получаем:

M Xm ( k ) = Ne ^ IX o ( r , 0 , Ф ) х 2 mc

“ V х — kxeikxr^m0 (r, 0 ф) +

Получив матричные элементы, можно рассчитать компоненты тензора диэлектрической проницаемости. Для этого преобразуем формулу, учитывая тождественность электронов и вынося общий множитель за скобки, а также факт, что величины в зависимости должны быть без-

размерными.

Диагональные компоненты представляются

+ 2 ie ik x r “X_V m 0 ( r , 0 , ф ) dV .

системой:

После чего интеграл можно разбить на

^_    Ne h

M nm (k) =     х nm

2 mc

S in ⁾⁽ ® , ^k) =

два:

= 1 —

4 п    I Ne ² c ^{2 (} Ne h r ] ) 2

(to0to')2 v m + h ^ 2mc ?

х

^х JX o^{( r} , ⁰ Ф ) k

_ V

e

^:ik x r Y m 0 ( r , 0 , ф) dV +

+ J 2 ie ik x r< o ( r , 0 , Ф ) V

a

T- ^Y m 0 ( ^r , ⁰ Ф ) ^dV • a x

_        _

M^lnm ( — k ) M mn ( k ) ® o ⁽®' ^— ® m + ® n )

M mn ( — k ) M ^m ( k ) 1 ® o ⁽®'+® m ^— ® n ) _?

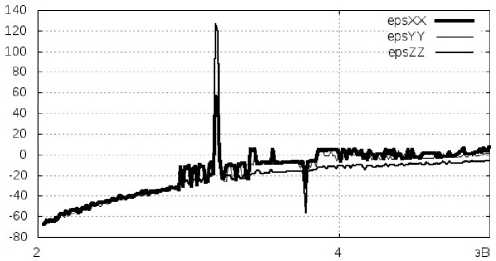
Рис. 2. Действительная часть диэлектрической проницаемости кремния без учета релаксационных процессов. Диагональные элементы £_-, £ , £_~. Гамма-точка зоны Бриллю-xx yy zz эна

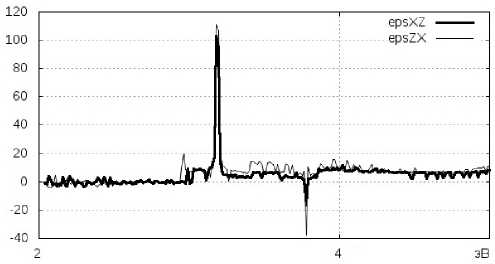
Рис. 4. Действительная часть диэлектрической проницаемости кремния без учета релаксационных процессов. Недиагональные элементы £ _Ж2 , £ z _K . Гамма-точка зоны Бриллюэна

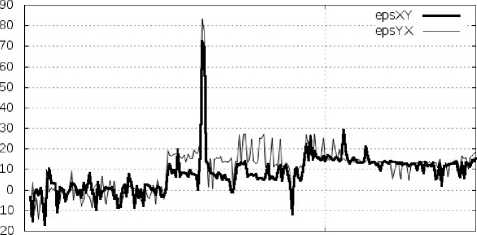
2 4 эВ

Рис. 3. Действительная часть диэлектрической проницаемости кремния без учета релаксационных процессов. Недиагональные элементы £ x , £ _уж . Гамма-точка зоны Бриллюэна

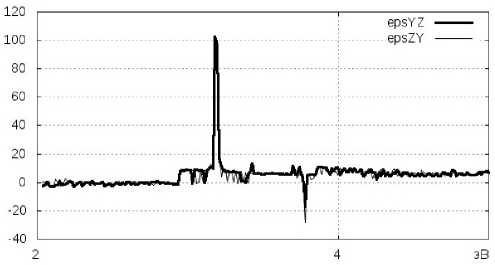
Рис. 5. Действительная часть диэлектрической проницаемости кремния без учета релаксационных процессов. Недиагональные элементы £ , £ . Гамма-точка зоны Бриллюэна yz zy

Далее:

Обозначая,

y n ) ( о , k = 1 -

( E 0 E f V V’

A =

4 п Ne 0 m 0

^, m ₀ V ₀ E ₀

N Й 0   ^f д V 0 ]

b =1I

^{4 m} 0 ^E 0 V ^r 0 )

.

f N (e0ef N2r4 (egef (^й')2 --+--n----------- v m0m'        4 (m0m')2

Все константы

£ in ) ( О , k ) = 1 -

в

СГС.

A I I 1 + B x V'IE'J I

z

m * n

M nm ( - k ) M^ mn ( k ) E 0 ( E '- E m + Е П )

-

M mn ( - k ) M nm ( k ) ' E 0 ( E ' + E m - E n )

После упрощения получаем:

£^ ) ( o , k ) = 1 -

4n Ne 0 k 0 ( Й ' ) ² m 0 V 0 E 0 V'

2 ft e I "E ^{7 J}

x

xZ

m * n L

f 1     N Й 0 Г 4 Й ' f 1 2

+ " I I m'   4 m 0 E 0   V m' )

xZ

m * n

M nm ( - k ) M mn ( k ) ( EE m + E n )

-

M mn ( - k ) M nm ( k ) ( e '+ E m - E n )

Учитывая, что Й ' = e' = c' = m' = 1, получаем:

£ in ^{)( o} , ^k) = ¹

4 n Nepho 1 f^ | ² m 0 VE 2 V 'I ^E 'J

f

^{1 +}

V

N ft 0 r 4 _x 4 m ₀ E ₀

xZ

m * n

M^lnm ( - k ) M^lmn ( k ) ( E '- E m + E n )

-

M^lmn ( - k ) M^lnm ( k ) ( E ' + E m - E n )

A

)

—

Mⁱnm ( - k ) M^lmn ( ? — ) M mn ( - k ) M;

—*

i

——

( E '- E m + E n )

-

nm

—

( k )

(E' + Em- En) JJ

.

E ' — в ридберг, V ' — в кубических борах.

Недиагональные компоненты выразятся формулой:

£ j ) ( to , k — ) =

xZ

m * n L

-

4 п c ²

—x

Й О ² V

M nm (- k ) M^mn ( k ) M mn (- k ) M^nm ( k ) --------------- — ---------------

о - о m + о n

(О + tom

-

to n

.

На рис. 2–5 приведены графики качественных

результатов на основании данных формул.