Расчет концентрации вакансий при термомеханическом нагружении

Эволюция вакансионной системы и зарождение пор под действием циклической термомеханической нагрузки определяют долговечность нанокристаллических двухфазных сплавов, например, жаропрочных сплавов, представляющих собой композиционные материалы, состоящие из кубических зерен Y фазы размером до 0,5 мкм и соединенных тонкими прослойками матричной Y фазы толщиной до 0,05 мкм [1-3]. В процессе эксплуатации сплавы испытывают комплексное воздействие нескольких эксплуатационных факторов: высоких нагрузок, вибрации, неравномерного циклического нагрева. Под действием термомеханических нагрузок происходит зарождение избыточных неравновесных вакансий, активация диффузионных процессов, рост пор. Парциальные коэффициенты диффузии компонентов различны, что также приводит к возникновению потоков вакансий в зернах и прослойках. Исследование кинетики вакансий, роста и залечивания пор в никелевых жаропрочных сплавах в технологиях залечивания пористости было проведено в работах [4-6]. Однако кинетика возникновения и развития избыточной концентрации вакансий при различных видах термомеханического нагружения, которые возникают при эксплуатации, до настоящего времени не исследована.

Целью работы является проведение расчета концентрации вакансий в одномерной модели при термомеханическом нагружении, включающем циклические напряжения растяжения, темпе- ратурные напряжения и нагрев до высоких температур с учетом микроструктуры.

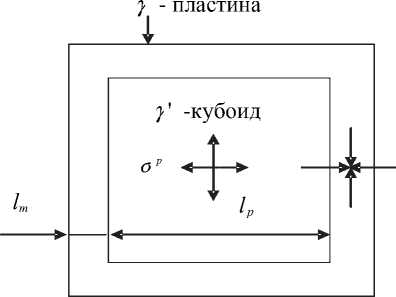
Рассмотрим бесконечную изотропную пластину, находящуюся под действием постоянных и циклических растягивающих напряжений вдоль и температурного градиента поперек пластины. Для решения задачи об определении межфазных напряжений нужно рассмотреть периодическую ячейку у'/ у-микроструктуры, состоящую из Y -кубоида, окруженного у -оболочкой, которая в свою очередь состоит из трех у -пластин, трех у-брусьев и маленького Y-кубоида (рис. 1). В данной статье исследуется задача с учетом изменения коэффициента диффузии при наличии циклических напряжений и градиента температуры.

o ^m

Рис. 1. Схематическая микроструктура жаропрочных никелевых сплавов

В процессе нагружения возникает избыточная неоднородная неравновесная концен- трация вакансий. В условиях непрерывного изменения температуры развиваются напряжения, возникающие вследствие разницы коэффициентов термического расширения фаз. Кинетика вакансий определяется диффузионным уравнением с источником вакансий по термактивационному механизму с учетом диффузионных и термических напряжений, а также концентрации напряжений возле включений [7–11]. Межфазные (когерентные) напряжения в γ'/γ-микроструктуре не-деформированных жаропрочных никелевых сплавов возникают из-за разности параметров γ- и γ' -решеток.

В работах [12–14] межфазные напряжения рассчитывали в двумерном приближении (плоское деформированное состояние). Согласно принятым допущениям, напряженное состояние периодической ячейки описывается двумя компонентами напряжений σ m и σ p (рис. 1).

За счет работы термомеханических нагрузок происходит зарождение избыточных вакансий. Кинетика изменения плотности избыточных вакансий в первом приближении описывается уравнением [7]

^{∂ c} +∇ D ∇ c = ^{c - c 0} ,                                (1)

∂ t              τ ₀

где c – избыточная плотность вакансий, c 0 – равновесная плотность вакансий, τ 0 – среднее время жизни вакансий до поглощения стоками (дислокациями, границами и др.), D – коэффициент диффузии вакансий. Характерное время жизни вакансии до поглощения в стоке оценивается выражением [7]

τ 0 = l ² p / D ,                                          (2)

где l – среднее расстояние между стоками, p – коэффициент прилипания вакансии. В зависимости от плотности стоков время жизни вакансий может изменяться от 10 до 10³ с.

В упругом поле напряжений σ и температур T в изотропной среде вакансии будут обладать химическим потенциалом, который может быть представлен в виде [7]

μ = kT ln( c ) - 1 Ω σ + k^T T ,                             (3)

• c ₀   3 cD

где Ω – мощность вакансии, характеризующая изменение объема кристалла при образовании в нем вакансии, Ω= 3 ⋅ 10 ^- 29 м 3 , k T – термодиффузионное отношение, σ = 0 ÷ 1,8 ⋅ 10 8 Па . Первое слагаемое описывает диффузию вакансий, второе и третье слагаемые характеризуют дрейфовое движение вакансий под действием неоднородных напряжений и температуры соответственно. Равновесная концентрация вакансий определяется соотношением

• - E + σ Ω

c ₀ = exp(         ) ,                                       (4)

kT где E – энергия образования вакансии. Систему уравнений (1)–(4) необходимо дополнить граничными условиями. На неравновесную концентрацию вакансий оказывают влияние концентрационные и диффузионные напряжения, циклическая термомеханическая нагрузка. Величина концентрационных напряжений зависит от размерного несоответствия атомов и модулей сжимаемости компонентов. Диффузионные напряжения возникают вследствие неравных встречных потоков атомов компонентов. В первом приближении в линейной теории упругости суммарные напряжения будут определяться выражением [5–8]

σ ( r ) = σ ₀ + K ₀ Ω c + σ ₁ - K ₀ α _TT ( r) ,                         (5)

где σ 0 , σ 1 – значения напряжений центробежных растяжения и вибрационных соответственно, Т = 1193 ÷ 1293 К , K 0 – модуль всестороннего сжатия, α T – коэффициент теплового расширения. Первое слагаемое описывает растягивающие центробежные напряжения, второе и третье слагаемые характеризуют концентрационные и вибрационные напряжения, последнее – термоупругие напряжения.

При взаимодействии одиночных избыточных вакансий в поле напряжений и температур возникают неустойчивости, приводящие к образованию кластеров вакансий. Избыточная плотность вакансий c определяется выражением

Δc=c-c0=c0 + c0exp( ), (6) D kT где ΔD =Dm-Dp; Dm, Dp – коэффициенты диффузии в пластине и кубоиде соответственно. Решение системы уравнений (1)–(6) возможно только численными методами. Для упрощения задачи рассмотрена усредненная по срединной линии γ' -кубоида, одномерная стационарная задача для слоистой системы, состоящей из γ'/γ- микроструктуры с толщиной lp /lm соответственно, где lp =0,5 ⋅10-6 м , lm =0,05 ⋅10-6 м [7, 8]. Задача рассматривается при условии, что величины зависят только от координаты х. На границах заданы условия непрерывности для концентрации и плотности потока вакансий.

На рис. 2 приведены относительные профили неоднородной концентрации вакансий в γ '/ γ -микроструктуре, полученные при численных расчетах стационарной одномерной задачи и показывающие пространственные распределения вакансий вдоль оси х . Рис. 3 и рис. 4 показывают изменение избыточной плотности вакансий при воздействии вибрационных напряжений и температуры, соответственно. Изменения значений Δc на рис. 3 соответствуют переменным воздействиям вибрационных напряжений с течением времени.

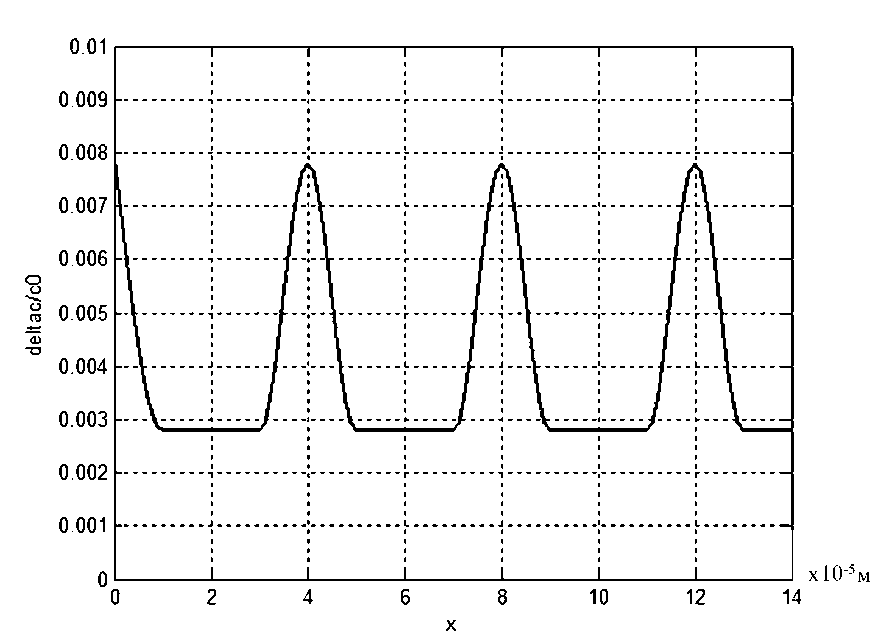
Рис. 2. Профиль зависимости неоднородной стационарной концентрации вакансий от расстояния x в зернах γ ' - фазы и γ - прослойке при действии растяжения σ ₀ = 1,8 ⋅ 10⁸ Па и температуры Т = 1100 К

При моделировании использованы следующие значения параметров: σ 0 = 180 МПа , α _Tm = 18,1 ⋅ 10 ^{- 6}K ^{- 1}, α _Tp = 11,9 ⋅ 10 ^{- 6}K ^{- 1}, Т = 1100К , D_p = 3,2 ⋅ 10 ^{- 14} м²/с, D_m = 2 ⋅ 10 ^{- 13} м²/с, σ ₁ = 5 ⋅ 10⁷ Па, τ ₀ = 10с.

Таким образом, в наноструктурном сплаве при термомеханической нагрузке возникает значительное пересыщение неравновесных вакансий.

Рассматривая решетку с избыточными вакансиями как пересыщенный раствор, можно рассмотреть различные механизмы их релаксации, например, образование и рост пор. В рамках механизма диффузионно-деформационной неустойчивости при достижении критического значения избыточных вакансий может возникнуть явление восходящей диффузии, когда малые локальные флуктуационные превышения концентрации вакансий начинают расти. Рост обусловлен снижением энергии Гиббса в области повышенной концентрации вакансий, вызванным действием термомеханических напряжений. Для зависимости скорости роста флуктуации r F от времени можно использовать уравнение [7] r F = D A c v / rc 0 .

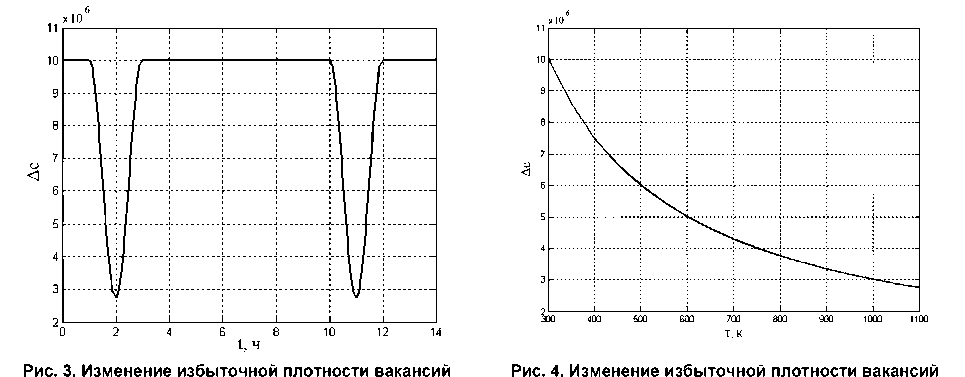
в зависимости от времени в зависимости от температуры

Используя параметры для никеля можно оценить время зарождения t_F ≅ 10 ^{- 1} c . Благодаря перес ыщению ва кансий флуктуация может расти в виде поры до размера r_П за время t_з : r_П ≅ 2 D Δ c_vt_з / c ₀ ≅ 0,5 ⋅ 10 ^{- 6}м.

Исследование жаропрочного никелевого сплава ЖС32-ВИ в монокристаллических охлаждаемых рабочих лопаток ТВО методом растровой электронной микроскопии показало, что при действии растягивающих напряжений при средней температуре 1100К поры размером до 1 мкм образуются в γ′- матрице [4].

Таким образом, полученное соответствие теоретических оценок с экспериментальными данными говорит об адекватности предложенной модели.