Расчет методом Дугласа-Кролла-Кона-Шэма g-тензоров ЭПР

Введение. Качество продуктов определяется по концентрации свободных радикалов в них. Свободные радикалы вырабатываются в продуктах в результате окислительно-восстановительных реакций. Для понижения концентрации свободных радикалов в продуктах и повышения их срока хранения добавляются специальные антиоксидантные вещества [1, 2]. Концентрация свободных радикалов должна измеряться в конечном продукте, так как пищевые продукты различаются по химическому составу и по-разному влияют на активность свободных радикалов. Методы измерения процентного содержания свободных радикалов и контроля качества являются важной составляющей пищевой промышленности. При исследовании качества продуктов измерения проб проводят методом электронного парамагнитного резонанса (ЭПР) [3]. Метод ЭПР обеспечивает непосредственное определение концентрации свободных радикалов в продуктах независимо от плотности и оптических свойств. С другой стороны отнесение ЭПР-сигналов к тем или иным функциональным группам, в конечном счете, определяется по их соответствию адекватным теоретическим моделям. В настоящее время для описания электронного строения сложных объектов, как правило, используется метод функционала плотности. В стандартном однокомпонентном варианте данного метода g-тензоры ЭПР описываются функциями нерелятивистского гамильтониана с релятивистскими поправками второго порядка теории возмущения. В этой связи составляющие ЭПР сигнала атомов тяжелых элементов представлены хуже составляющих легких элементов. Ситуация может быть улучшена при использовании функций двухкомпонентного метода, в котором ЭПР-сигнал оказывается свойством, описываемым в первом порядке теории возмущения и соответствующие поправки линейны от заряда ядер атомов.

Цель исследования: развитие подобной расчетной схемы в рамках метода Дугласа-Кролла-Кона-Шэма. Данный метод основан на разделении позитронных и электронных состояний посредством эффективного проектирования четырех компонентных Дираковских состояний в пространство электронных решений. В базовом варианте метода (учет до 96 % релятивистских составляющих энергии связи) проекторы в электронное пространство определяются потенциалом притяжения к ядрам и не зависят от потенциала обменно-корреляционных взаимодействий. В работе решались научные задачи представления формул расчета компонент g-тензора для базового варианта метода Дугласа-Кролла и определения особенностей воспроизведения данной расчетной схемой экспериментальных g-тензоров радикалов: CO+, CN, NO2, NF2, HCO, C3H5, TiF3, RhC, PdH. В дальнейшем такие расчеты g-тензоров были использованы для интерпретации особенностей спектров ЭПР-катализаторов [4].

Расчет g-тензора электронного парамагнитного резонанса. Гамильтониан четырехкомпонентного метода Дирака-Кона-Шэма может быть написан с использованием эффективного одночастичного потенциала υ eff , определяющего взаимодействия в некоторой многоэлектронной системе:

^̂ = ⃗∙ ⃗+ + , (1)

где p – механический импульс; с – скорость света; α и β – 4 × 4 матрицы Дирака.

Гамильтониан определяет решения как для электронов, так и для позитронов. Позитронные состояния не представляют химического интереса, и при решении химических задач их наличие приводит лишь к ряду существенных осложнений. Избавиться от позитронных решений можно трансформируя гамильтониан, используя унитарное преобразование Дугласа-Кролла U :

/ 2 ,           -  -\ а л„      а п .       c + v„ff     ca • pt hDDK = uh du f = и      eff    ,и

I ca • p   - c + V eff ,

ˆ ^DK

^H (2)

0  1

где ст - матрицы Паули, о = ( a x , a y , a z) . Преобразование U разделяет четырехкомпонентное уравнение на два двухкомпонентных уравнения: электронное – ^̂_{( )}Ѱ =ЕѰ и позитронное – ^̂_{( )} Ѱ =Е Ѱ . Отметим, что решения связаны друг с другом с помощью преобразования U:

Ѱ = Ѱ=Ѱ .

При расчете средних значений операторов нужно принимать во внимание так называемое изменение картинки [5]. Для изменения энергии первого порядка Δ E^Z системы

̂ Ѱ= Ѱ , вызванного зеемановским возмущением гамильтониана, запишем

( ̂ + ̂ , )Ѱ=( +Δ )Ѱ.

Использование с данным оператором волновой функции метода Дугласа - Кролла (смешанная картинка) приведет к ошибочному результату:

Δ ^̃ =〈Ѱ | ^{̂ ,} |Ψ 〉≃0 .

Это отражает тот факт, что оператор Зеемана

H ^D , Z =

0 a • A

a • A 0

является недиагональным и ненулевые матричные элементы могут появляться только между электронными и позитронными решениями. Заметим, что оператор ^{̂ ,} был получен заменой в выражении (1) обычного импульса на калибровочно - инвариантный импульс:

⃗⟶ ⃑⃑= ⃗+ ⃑⁄ , при этом нами вводится зависимость от магнитного поля B, поскольку

1 =  (  ×⃑).

Правильное выражение в рамках формализма Дугласа - Кролла для первого порядка изменения энергии Δ E^Z во внешнем магнитном поле B , входящем в оператор ^{̂ ,} , записывается как

Δ =〈Ѱ |  ^{̂ ,} |Ψ 〉․        (2)

Здесь мы остановимся на варианте метода с гамильтонианом ^̂ _{( )} , диагональном во втором порядке по (υ eff / E ) [6, 7]

HHDK ,1 = UU0 HI DU^U / = й DK ,1

Л (2)

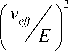
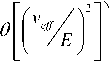
H

DK ,1

Таким образом, чтобы получить H ˆ ^Z , требуется преобразование U 1 U 0 дираковского зеемановского оператора - ^{̂ ,} . Преобразование для свободного электрона Фолди-Ваутхойзена

U 0 = A p ( 1 + P R ) = A ( 1 + K_r P ^a • p ) = A p [_ _K d . _p K ^ ' ^p ] ⁽³⁾

Hi DK ’ ^Z = l₊ uh D , ^z u _o^fL₊ ^f =

(     1

^x<  ^{K d} • ^p

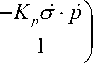
A p L ₊ ^f.

может быть выражено в простой аналитической форме. Здесь релятивистские кинематические факторы

A p = ^( E p + c ²)/2 E p

c

^Kp = A E p + c ²) ^, R p = ^K _P ^{( a p} )

зависят от обобщенной релятивистской кинетической энергии

= √  +․

Дополнительное преобразование U 1 определяется значительно более сложным выражением, согласно [6, 7]:

=√1+   +,

;    ,                                    ;,

; ,  =    (      +    -    +       )․

Для вычисления составляющих в среднем значении 〈Ψ |  ̂ , |Ψ 〉 можно ограни читься только преобразованием U0, тогда

Δ ≃〈Ψ |   ̂ , |Ψ 〉․

Чтобы отразить эквивалентность применения преобразования либо к оператору или к волновой функции, также можно записать

(? U \u 0 H D ^, Z U 0 ^f| ? U} = U o^f ? U | H D,^Z I U J ^ U ) .

Рассмотрим преобразование

̂ ,  → ̂( ), =ℒ ̂ , ℒ , здесь проектор L+ выделяет электронную часть матриц четырехкомпонентной задачи. Более подробно:

Поэтому

H^Z - HI DK-Z = A p [ K p ( a • p ) ( ^d • A ) + ( & • A ) ( d • p ) K p ] A p . ₍₄₎

К р и (о- р ) коммутируют, поскольку К р является функцией р² коммутирующего с компонентами р . С помощью соотношения Паули запишем

( а • p ) ( a • A ) = pA + i d ( p x A ) .

Используя ⃗=- ∇ и ^⃑⃗=∇×^⃑⃑⃑⃗, получим для любой волновой функции Ψ

^ ( a • p ) ( d • A ) ]? = ^ pA + b_ — &  ( A xv ) ]? =

= [ p • B + A • p — i d ( A x p ) ]? .

Здесь используется соотношение

⃗∙ ^⃗Ψ=( ⃗∙ ^⃗)Ψ+ ^⃗∙ ⃗Ψ ,

где скобки указывают на то, что р действует только на А. Первый член правой части исчезает из-за того, что кулоновская калибровка ∇ ^⃗= ка?Л = 0 . Для получения члена ( о • ВФ ) было использовано соотношение ^⃑⃗=∇× ^⃗ . Для оператора можно записать

^⃗∙ ⃗= (^⃑⃗×⃗)∙ ⃗= ^⃑⃗∙(⃗× ⃗)= ^⃑⃗∙^⃑⃗, (6)

где ⃑⃗=⃗× ⃗. Для третьего члена запишем д (p x A ) = ~d ^( B x r )x p ] =

= ¹ ( ^a • r ) ( ^B • ^p ) ^{— 1} ( ^a • ^B )⁽ r • ^p ).     _m

^{2                 2                      (7)}

Аналогично, для второго члена уравнений (1) и (4) получаем

( d • A ) ( d • p ) ? = ^ A • p + i d ( A x p ) ]? .

Правая часть упрощается применением цепочки преобразований, таких же, как и в случае выражения (2). Уравнение (1) для зеемановского гамильтониана преобразуется к выражению

H Z = 2T ° ’ B + a p [ K P ( A ‘ p ) ⁺ ( A ’ p ) K P ] a p -- iA P [ ^Kp ° ■ ( A ^{x p} ) - ° ■ ( A ^{x p} ) K P ] a p .

.

С использованием уравнений (3) и (4) получаем

H Z = y° ° ' B + 1 A p [ ^kp ( L • B ) + ( L • B ) K p ] a p +

2 E_p      2

+1 A p { K p [ ( ° • B ) ( r ^Н ° ' r ) ( B '^v ) ]-[ ( ° • B ) ( r •^v ) - ( ° • r ) ( B •v ) ] K p } A p .

Первое слагаемое (о- В ) - зеемановское взаимодействие электронного спина и магнитного поля. Следующий член ( L · В ) описывает орбитальное зеемановское взаимодействие, обусловленное орбитальным движением электрона в магнитном поле B . Последний член напоминает зеемановский спин-орбитально-калибровочно-коррекционный член. Если K p и оператор в скобках коммутируют, то данный член будет равен нулю. Пренебрегая последним членом и вводя электродинамическую поправку g e /2 для первого вклада, в которой g e = 2,002319 – g-фактор свободного электрона, мы получаем окончательную рабочую формулу

H Z = — ° • B + ¹A Г k„(l • B )+( l • B}k„ ] A .

4 E_p 2 ^{p [ ;}' ^{n p p] p} ^

Тестовые расчеты. В качестве тестовых систем для апробации нового метода расчета g-тензоров нами использованы два набора неорганических радикалов: CO+, CN, NO2, NF2, HCO, C3H5, TiF3, RhC, PdH (табл. 1). Набор радикалов позволяет выполнить сравнение с экспериментом и с результатами других расчетов высокого уровня. Рассчитанные величины зеемановских сдвигов Δg, уравнение (8), незначительны для молекул легких атомов. Общий сдвиг расчетных g-тензоров Δg молекул легких атомов опреде- ляются орбитальными зеемановскими вкладами ΔL, уравнение (8). Расчетные сдвиги воспроизводят экспериментальные сдвиги молекул легких атомов: относительные сдвиги основных компонент, их знаки и общие характеристики, прослеживаемые в спектрах ЭПР. Однако расчеты систематически переоценивают анизотропию сдвигов g-тензоров молекул, образованных атомами основных групп. Это указывает на переоценку спин-орбитального взаимодействия, в первую очередь отвечающего за сдвиги g-тензоров. Такая переоценка связана с пренебрежением двух электронных составляющих спин-орбитального взаимодействия, обусловленным не учетом соответствующих вкладов в матрицах преобразований Дугласа-Кролла. Добавка электрон-электронного потенциала Хартри при построении проекторов Дугласа понижает до 30 % (или более) орбитальный зеемановский вклад ΔL для всех радикалов легких элементов. Это приводит к систематическому улучшению соответствия с экспериментальными данными. Дальнейшее улучшение возможно при использовании релятивистских преобразований, зависимых от обменно-корреляционного потенциала. Для молекул NO2 и НСО, результаты ДКН-расчета особенно близки к данным методологически аналогичного подхода ZORA ФП [8].

Расчет g-тензоров радикалов переходных металлов представляет собой более сложную задачу, чем расчет g-тензоров молекул элементов главных групп. Результаты ДКН-расчетов для TiF 3 , RhC и PdH таблицы находятся в соответствии с данными других расчетов[8], также наблюдается качественное согласие с экспериментальными данными [9–12].

Расcчитанные и экспериментальные значения Δg ×105

Радикал	Компон.	Экспер. значения	Расчеты DKH	Радикал	Компон.	Экспер. значения	Расчеты DKH
CO+	┴	-240 [9]	-350	HCO	xx	150 [15]	303
	║		-22		yy	0	-20
CN	┴	-200 [10]	-270		zz	-750	-1076
	║		-20	C 3 H 5	xx	0 [15]	-13
NO 2	xx	390 [11]	472		yy	80	96
	yy	-1130	-1513		zz	40	76
NF 2	xx	-10	-37	TiF 3	┴	-11130 [12]	-4526
	yy	620 [13]	1027		║	-1110	-28
	zz	280	603	PdH	┴	29088 [14]	24735
RhC	┴	5178 [14]	4680		║	-3732	-1818
	║	-158	-173

В DKH расчетах использовались следующие базисные наборы [16]: для H (8s5p1d) →

[5s4p1d], для C, N, O, F (13s8p7d) → [8s7p3d], Ti (15s11p6d5f)    →    [10s11p6d1f], Rh, Pd

(18s13p9d8f8g) → [10s12p9d3f1g].

Заключение. В данной работе была развита схема расчета компонент g-тензора ЭПР для систем с дублетными спиновыми состояниями на функциях двухкомпонентного метода Дугласа-Кролла. Рассчитаны g-тензора ЭПР спектров радикалов CO+, CN, NO 2 , NF 2 , HCO, C 3 H 5 , TiF 3 , RhC, PdH. Проведено сравнение расчетных тензоров и тензоров, полученных экспериментально. Для рассмотренных тестовых систем предложенный метод расчета g-тензора ЭПР дает сдвиги компонент, которые соответствуют их экспериментальным значениям с систематической погрешностью, связанной с переучетом в базовой версии метода силы спин-орбитального взаимодействия.