Расчет на прочность цилиндров с отверстием при совместном использовании метода граничных элементов и нелокальных критериев разрушения

Рис. 1. Схема нагружения путем сжатия по диаметру полого цилиндра

Учитывая хрупкий характер

цилиндра при сжатии его по диаметру (называемым «бразильским тестом»). Однако в этом случае напряженное состояние в окрестности точки начала разрушения является резко неоднородным. Это обстоятельство приводит к необходимости прибегать к нелокальным критериям разрушения для оценки уровня разрушающей нагрузки в испытаниях модифицированным бразильским методом.

Найти напряженное состояние цилиндра при его сжатии по диаметру позволяет известное из теории упругости решение [6]. Для цилиндров с центральным круговым отверстием, диаметр которого много меньше диаметра цилиндра, с помощью суперпозиции решений Кирша можно получить формулы, описывающие напряженное состояние в окрестности отверстия. Однако при наличии у цилиндров отверстий и вырезов, размеры которых сопоставимы с размерами цилиндра, оценить напряженное состояние можно только приближенными, в том числе численными методами, например методом граничных элементов [7, 8]. разрушения цилиндров с отверстиями, определить напряженное состояние перед разрушением можно также одним из методов граничных элементов, в частности, известным методом фиктивных нагрузок [9].

В случае использования градиентного критерия разрушения [10, 11], учитывающего неоднородность напряженного состояния, необходимо знать не только компоненты напряженного состояния, но и их производные по пространственным координатам. В этой связи при совместном приложении градиентного критерия и метода граничных элементов возникает проблема, обусловленная тем, что напряжения в окрестности средних точек граничных элементов вычисляются с большой погрешностью [9, 12]. Поэтому успех одновременного применения градиентного критерия и метода граничных элементов заключается в разработке алгоритма, позволяющего с высокой точностью вычислять напряжения во внутренних точках тела, находящихся в окрестности средних точек граничных элементов.

• 2.    Нелокальные критерии разрушения

В градиентном критерии для определения нагрузки в момент начала разрушения сравнивается с пределом прочности материала ст в не максимальное, а эффективное напряжение ст e. Эффективное напряжение пропорционально в рассматриваемой точке тела максимальному растягивающему

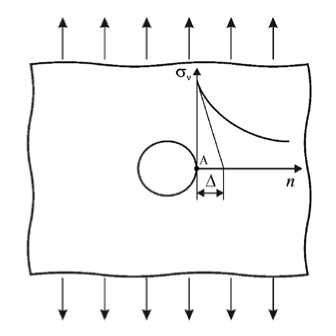
Рис. 2. Условный размер Д зоны концентрации напряжений

напряжению ст 1 , которое принимается в качестве эквивалентного. Кроме того, ст e зависит от локальной неравномерности поля напряжений в окрестности рассматриваемой точки и представительного размера неоднородности материала. Локальная неравномерность распределения напряжений характеризуется относительным градиентом g _v = grade _v | /ct _v положительного нормального напряжения ct _v , действующего на плоскости, включающей площадку первого главного напряжения в рассматриваемой точке тела, где плоскость и площадка имеют общую нормаль v . Вычисление grad g_v| в некоторых задачах осуществляется проще, чем gradσ ₁ , использовавшегося ранее [10, 11]. Величиной, обратной относительному градиенту g _v , является

Д — условный размер зоны концентрации напряжений в рассматриваемой точке A (Рис. 2).

Относительный градиент находится в результате решения соответствующей задачи теории упругости. Выражение для эффективного напряжения записывается

в виде:

механикой разрушения и выражается через известные характеристики материала — предел прочности σ _в и критический коэффициент интенсивности напряжения K _{I c} — по формуле:

L 1 = ( 2 π ) K I² c σ в² . (2)

Значение параметра аппроксимации устанавливается для конкретного материала исходя из удовлетворительного описания экспериментальных данных по разрушению образцов с концентратором напряжений определенного вида. В последующем оно может быть использовано для элементов конструкций из того же материала с другими концентраторами напряжений.

Будем считать, что разрушение в окрестности рассматриваемой точки начинается при достижении эффективным напряжением σ _e значения предела прочности материала и первоначально распространяется по площадке действия максимального растягивающего напряжения. Дальнейшее направление разрушения может отличаться от первоначального.

В критерии разрушения по напряжению в удаленной точке (критерии Нуизмера) сравнивается с пределом прочности материала σ _в нормальное напряжение σ _ν в точке, расположенной на некотором расстоянии r _∗ от рассматриваемой точки действия максимального напряжения. Расстояние r _∗ находится в [13] из условия согласования с теорией трещин:

r ∗ = ¹ K I² с σ в² = ¹ L 1 . (3) 2π4

• 3.    Численный алгоритм

На основе градиентного критерия и метода граничных элементов (в варианте метода фиктивных нагрузок) был разработан численный алгоритм для расчета на прочность. При этом его характерная особенность состоит в том, что в ходе вычислений необходимо определять не только компоненты напряженного состояния, но и их производные по пространственным координатам.

При использовании метода граничных элементов возникает проблема, связанная с тем, что напряжения во внутренних точках могут быть найдены с удовлетворительной точностью лишь при условии, что эти точки удалены от контура на расстояние, большее длины одного элемента [9]. В связи с этим требовался алгоритм, позволяющий с высокой точностью вычислять напряжения в точках тела, расположенных вблизи границы.

Предлагаемый численный алгоритм определения напряжений вблизи границы тела включает в себя два этапа. На первом этапе находим напряжения σ ⁱ _ν в средних точках граничных элементов и производные по касательной к контуру ∂σ ⁱ _ν /∂ s в этих точках. На втором этапе в теле на малом расстоянии I ∆ n от граничных элементов основного контура проводим новую эквидистантную гранично-элементную ломаную линию, образующую вспомогательный контур. Используя уравнения равновесия бесконечно малого элемента на контуре тела, получаем приближенно граничные условия для вспомогательного контура через найденные ранее значения напряжений σ ⁱ _ν на основном контуре и производных ∂σ ⁱ _ν / ∂ s . Применяя метод граничных элементов к задаче с заданными граничными условиями на вспомогательном контуре и вычисляя напряжения в центре каждого граничного элемента этого контура, фактически находим напряжения в интересующих внутренних точках исходной задачи, но уже с более высокой степенью точности.

Производные нормального напряжения, необходимые для вычисления модуля градиента, определяем согласно конечно-разностным формулам численного дифференцирования. При этом для вычисления производной ∂σ ⁱ _ν /∂ s нормального напряжения по касательной s к контуру пользуемся трехточечным шаблоном численного дифференцирования с неравными шагами, для производной ∂σ ⁱ _ν I ∂ n нормального напряжения по нормали n к контуру — двухточечным шаблоном. Подставляя известные теперь в каждой из средних точек граничных элементов значения σ ₁ и g _ν в выражение (1) для σ _e , находим точку, где эффективное напряжение максимально, то есть устанавливаем место начала разрушения.

В общем случае кривизна контура концентратора может быть не постоянной, а переменной величиной. Поэтому для выяснения вида граничных условий на вспомогательном контуре воспользуемся дифференциальными уравнениями равновесия из [14] для плоской задачи в произвольной криволинейной ортогональной системе координат ( α ₁ , α ₂ ), а не в цилиндрической как в [15]. Рассмотрим первое из этих уравнений:

a . a , ан. ан.

—(H 2g, J + —(H, Gj 2) +—1 g12--2- g22+ HHF = 0.(4)

2 11                    1 12                 12                22        12 1

da,          da2          da2

Здесь: H ₁ , H ₂ — коэффициенты Ламе, представляющие собой отношения приращений длин координатных линий a ₂ = const или a , = const к соответствующим приращениям d a , или d a ₂ криволинейных координат

H 1 = ^ ( d x/ da , ) 2 + ( d y /da , ) ² ,

H2 = ^(dx/da2 )2 +(dy/da2 )2 , где an, ст12, ст22 — компоненты тензора напряжений, F, — проекция объемной силы на координатную линию a,.

Возьмем такую систему координат, в которой контур концентратора описывается уравнением a , = const. Если предположить, что в рассматриваемых задачах объемные силы отсутствуют и на контуре концентратора равны нулю нормальные — ст ,, , и касательные — ст ,₂ , напряжения, то уравнение (4) на свободном контуре запишется в виде:

h 2 £1^ -ащ G 22 = о,

2 da, da, где ст22 — тангенциальное напряжение.

Пусть при переходе от i -го граничного элемента контура к следующему приращение параметра a ₂ постоянно: Aa ₂ = const. Так как длина элементов A s¹ = 2 а¹ при этом изменяется, то коэффициент Ламе H 2 = A s¹ /Aa ₂ = 2 a¹ /Aa ₂ у каждого элемента будет своим.

Далее будем считать, что при переходе от основного контура к вспомогательному, построенному по вышеописанной методике, параметр a , получает приращение Aa , = const. При этом приращения Aa ₂ по длине соответствующих элементов двух контуров остаются постоянными. Однако граничные элементы удлиняются на величину 2 A a¹ , где A a¹ — приращение полудлины 1 -го элемента при переходе от основного контура к вспомогательному. Следовательно, параметр H 2 увеличивается на A H 2 = 2 A a¹ /Aa ₂ .

Для использования в численном алгоритме запишем производные в уравнении (5) через приращения соответствующих параметров и координат:

( 2 a¹ /Aa ₂ )■ A ^{G 11}

—

(2A a1 /Aa2)

Aa ,

g 22 = о.

Из этого уравнения, учитывая, что Aa , = const, Aa ₂ = const, g 1 , = g ” , где ст n — нормальное напряжение на основном контуре, при g 22 = g V >  0 найдем приращение Ag ” при переходе к вспомогательному контуру:

^{A g} ”

A a .

=      ^G V .

ai

Так как на основном контуре        , то окончательно одно из двух граничных условий n1

на вспомогательном контуре примет вид:

,1 _ ^A a¹

^G ” 2       ‘ ^GV.

² aⁱ

Заметим, что уравнение (6) совпадает с уравнением, полученным с помощью условий равновесия в полярной системе координат [15].

Для выяснения вида следующего граничного условия рассмотрим второе из двух дифференциальных уравнений равновесия из [14]:

^( H о ) + ^( H 1 ^ 22 ) +     ^ 12 ^д H «И + H 1 H 2 F 2 = 0,                  (7)

да ₁           да ₂           да ₁       да ₂

где F 2 — проекция объемной силы на координатную линию а ₂ .

Так как в рассматриваемых задачах объемные силы отсутствуют и на контуре концентратора о_п = 0, о ₁₂ = 0, то уравнение (7) на свободном контуре принимает более простой вид:

H 6= 12 ^     H 5 0 ,2 = 0.

2                      22       1

да 1 да 2         да 2

Разделив в этом уравнении все члены на H ₁ и H ₂ , выразим первый член через остальные:

— " = ¹       - ¹ H = 0.                               (8)

H ₁ да ₁    H ₂ да ₂ H ₁ H ₂ да ₂ ²²

Поскольку по определению коэффициенты Ламе H ₁ и H ₂ представляют собой отношения приращений длин д n , д s координатных линий к соответствующим приращениям да ₁ , да ₂ криволинейных координат, из (8) получим уравнение:

д о ₁₂ = д о ₂₂     1 д H ₁

д n д s   H ₁ д 5 ’

Для использования в численном алгоритме некоторые производные в уравнении (9) перепишем в приращениях:

Л о ^ ₂      д о 22     1 A H ₁ i

---- =-----_ о^

A n д s   H ₁ A s i

Согласно методике построения вспомогательного контура все его элементы удалены от соответствующих элементов основного контура на одинаковое расстояние |A " = const, то есть он образуется параллельным переносом. Приращение внешней нормали A n при таком переносе для всех элементов отрицательно: A n =-|A n | = const. Параметр а ₁ при переходе от основного контура к вспомогательному также изменяется на постоянную величину Aa ₁ = const. Следовательно, H ₁ = A n /Aa ₁ представляет собой константу, и для всех элементов A H ₁ = 0 . Тогда последний член в уравнении (10) становится равным нулю, и отсюда, учитывая, что о ^ ₂ = о S , при о 2₂ = о V >  0 найдем приращение касательного напряжения σ ⁱ _s :

i

Aai=-——^A n.(11)

5д

Так как A n =-|A n | и на основном контуре c_s| = 0, то окончательно второе граничное условие на вспомогательном контуре запишется в виде:

о 5 L=^о^^ "I'

Уравнение (12) совпадает с уравнением, полученным с помощью условий равновесия в полярной системе координат [15]. Однако это обеспечивается самой методикой построения вспомогательного контура.

• 4.    Экспериментальные данные и численный анализ

Эксперименты проводились на модельном материале — эбоните. Из прутка эбонита диаметром 61 мм были изготовлены образцы в виде цилиндров радиусом R = 28 мм и толщиной t = 20 мм (см. Рис. 1), а также стандартные цилиндрические образцы с головками для захватов и рабочей частью диаметром 8 мм и длиной 35 мм для испытаний на растяжение. Ось вращения образцов в виде цилиндров совпадала с осью прутка. При испытаниях цилиндрических образцов на разрушение путем сжатия по диаметру между стальными плитами (бразильским методом) разрыв происходил по плоскости, проходящей через ось прутка, а при растяжении цилиндрических образцов с головками — по сечению, параллельному этой плоскости.

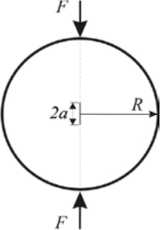
Рис. 3. Сжатие по диаметру цилиндрического образца с разрезом

Испытания четырех стандартных цилиндрических образцов на одноосное растяжение по диаметру прутка дали следующее среднее значение предела прочности: с в = 27,57 МПа (стандартное отклонение 3,76 МПа). Согласно бразильскому тесту на сжатие цилиндров по диаметру средний по четырем испытаниям условный предел прочности эбонита при растяжении составил: с _р = 23,69 МПа, (стандартное отклонение 2,46 МПа). Таким образом, условный предел прочности эбонита, найденный бразильским методом, оказался на 14% меньше стандартного предела прочности при одноосном растяжении.

По результатам испытаний трех цилиндрических образцов с центральным симметричным разрезом длиной 2a путем сжатия их по диаметру вдоль линии разреза (Рис. 3) для критического коэффициента интенсивности напряжений было получено значение K1 c = 1,119 МПа м1/2 (стандартное отклонение 0,086 МПа м1/2). Для этого использовалась формула из [16]: K 1 c = ^’О^2^F*- Y (X) ^X,(1 -X) , где F* — предельная сила, X — отношение полудлины t л]пR разреза к радиусу цилиндра, Y (X) = 1 - 0,60387X + 1,67239X2 - 1,16988X3. По установленным характеристикам эбонита, в соответствии с (2), найдено значение показателя неоднородности материала: L1 = 1,049 мм.

Из того же прутка были изготовлены цилиндры с центральными круглыми отверстиями, которые имели диаметр 1,4; 2 и 3 мм, что много меньше диаметра цилиндра, который равнялся 56 мм. Разрушение этих цилиндров осуществлялось путем сжатия их по диаметру между стальными плитами. Усилия сжатия моделировались сосредоточенными силами F (Рис. 1). Максимальное напряжение достигалось в точках пересечения контура отверстия с линией действия сил.

Численный анализ проводился с помощью программы расчета методом граничных элементов (в варианте метода фиктивных нагрузок) на языке Fortran, взятой из [9] и модифицированной под использование градиентного критерия. Внешний контур цилиндра, подобно контуру отверстия, разбивался на 360 элементов. Силы F моделировались как нормальное напряжение, приложенные к самому верхнему и самому нижнему граничным элементам.

В таблицах 1 и 2 приведены данные аналитического ( F _m ^а _ax ) и численного ( F _m ^ч _ax ) расчетов значений предельной нагрузки по градиентному критерию при в = 0 и критерию Нуизмера. Для сравнения показаны

Таблица 1. Результаты расчетов по градиентному критерию

Диаметр отверстия, мм	Количество образцов	F m э ax   , Н	F m а ax , Н	F m ч ax , Н
1,4	2	25792	27033	26957
2,0	3	23578	23938	23780
3,0	3	22205	21029	20692

Таблица 2. Результаты расчетов по критерию Нуизмера

Диаметр отверстия, мм Количество образцов Fmэax  , Н Fmаax , Н Fmчax , Н 1,4 2 25792 22548 22423 2,0 3 23578 17728 17555 3,0 3 22205 14162 13886 средние экспериментальные значения Fmэax . Отличие величин параметров в последнем и предпоследнем столбцах таблиц обусловлено двумя факторами: во-первых, аналитическое решение получено для бесконечной области, а численное — для конечной; во-вторых, численное решение имеет погрешность по определению.

В таблице 3 представлены максимальные растягивающие напряжения согласно аналитическому решению задачи ( ст max ), численному решению для бесконечной пластины с отверстием ( ^ max ) и численному решению для цилиндра с отверстием ( ст max ), а также эффективные напряжения ст а , ст e , ст Ч при приложении предельной номинальной нагрузки, рассчитанной аналитически по градиентному критерию разрушения. Из сопоставления видно, что для бесконечной пластины численные значения напряжений с точностью до четырех значащих цифр совпадают с найденными аналитически. Для цилиндров же с отверстием увеличение диаметра отверстия приводит к заметному превышению численных значений напряжений над значениями для бесконечной плоскости.

Таблица 3. К анализу значений максимального растягивающего напряжения

d , мм	ст mx , МПа	ст^„ , МПа	ст mx , МПа	ст a , МПа	ст р , МПа	ст e , МПа
1,4	92,20	92,20	92,47	27,57	27,57	27,65
2,0	81,64	81,64	82,22	27,57	27,57	27,76
3,0	71,72	71,72	72,95	27,57	27,57	28,02

По численным оценкам построены зависимости предельных нагрузок от диаметра отверстия в цилиндре (Рис. 4). При уменьшении числа элементов в два раза изменения расчетных данных не превысили 0,07% для градиентного критерия, 0,11% — для критерия максимальных напряжений и 0,26% — для критерия Нуизмера. Определение численных оценок предельной нагрузки по критерию максимальных растягивающих напряжений осуществлялось при условии разрушения ^max = ст в. Видно, что оно дает существенно заниженные по сравнению с экспериментальными данными величины разрушающей силы.

Для получения аналитических оценок предельной нагрузки использовалась суперпозиция двух решений Кирша: задачи растяжения и задачи

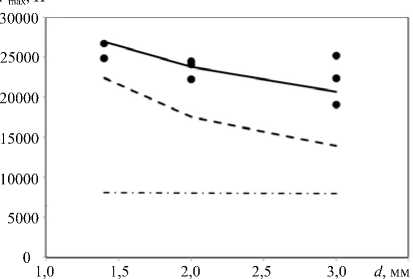
Рис. 4. Зависимости предельных нагрузок от диаметра отверстия: сплошная линия – градиентный критерий при р = 0; штрихпунктирная линия - критерий максимальных напряжений; штриховая линия – критерий Нуизмера; черные кружки – экспериментальные данные

трехкратного сжатия плоскости с круглым отверстием, поскольку в центре сплошного сжатого по диаметру сосредоточенными силами F цилиндра имеет место растяжение напряжением ст = F /( л Rt ) в направлении, перпендикулярном сжатию, и сжатие напряжением - 3 ст в направлении действия сил [26]. Максимальное напряжение наблюдается в точках пересечения контура отверстия с линией действия сил. Коэффициент концентрации напряжений составляет: а = 6, то есть отношение максимального напряжения на контуре отверстия

От точки максимума нормальное напряжение ст, зависимости (ее вывод приведен в [3]):

к номинальному растягивающему напряжению в центре сплошного сжатого по диаметру цилиндра, равно 6. Тогда по критерию максимальных напряжений предельная нагрузка вычисляется по формуле F max = ст _в п Rt /6 и равняется 8084 Н.

убывает вдоль линии действия сил по следующей

CT v =ст| 1 -

a ² a ⁴ — + 6— r ² r ⁴

Здесь a — радиус отверстия, r — текущий радиус (см. Рис. 1). На основе (13) получена формула для относительного градиента: gv = 11[(3a), от которого зависит эффективное напряжение. Эта формула использовалась также в [2-5]. После подстановки gv в (1) условие разрушения стe = ств дает оценку предельной нагрузки по градиентному критерию.

Согласно критерию Нуизмера нормальное напряжение ct_v вычисляется на расстоянии г , от точки пересечения контура отверстия с линией действия сил

ctv =ст 1 -

a ²

( a + r , ) ²

a .

(a + r-) ,

.

Условие разрушения ct_v =ст _в при r = a + r , на линии действия сил делает возможной оценку предельной нагрузки по критерию Нуизмера.

• 5.    Заключение

Для совместного применения градиентного критерия разрушения и метода граничных элементов в варианте метода фиктивных нагрузок разработан алгоритм, позволяющий с высокой точностью вычислять модуль градиента принятого эквивалентного напряжения. С помощью этого алгоритма достигнута достаточная для практических целей точность вычисления эффективного напряжения в градиентном критерии разрушения.

Проведено сравнение результатов расчетов по различным критериям прочности с экспериментальными данными по разрушению полых эбонитовых цилиндров при сжатии их по диаметру. Установлено, что локальный критерий максимальных напряжений дает существенно заниженные оценки разрушающей силы по сравнению с экспериментальными данными, полученными при хрупком разрушении образцов с концентраторами напряжений. Критерий Нуизмера приводит к более высоким значениям предельных нагрузок по сравнению с локальным критерием, однако они всё-таки меньше экспериментальных значений, в то время как величины предельной нагрузки по градиентному критерию наиболее близки к найденным экспериментальным путем.

Применение нелокальных критериев разрушения при проектировании конструкций с концентраторами напряжений позволит повысить при оценке их прочности уровень предельных нагрузок в том случае, когда размер зоны неоднородности напряженного состояния сравним с характерным размером неоднородности материала.

Работа выполнена при частичной финансовой поддержке РФФИ (проекты № 15-01-07631-а, 16-08-00713-а), также гранта Правительства Российской Федерации № 14.W03.31.0002.