Расчет на прочность и численный анализ оболочки расширителя котла

Расширитель периодической продувки котлов (рис.1) предназначен для сепарирования пара при аварийном сбросе давления из котлоагрегатов, откуда выбрасывается отдельно пар в трубопровод выхлопа, а вода-конденсат - в трубопровод слива. Рабочее давление Р_раб = 0.15 - 10⁶ Па , температура носителя-пара T = 120⁰ • C . Емкость расширителя

V = 7.5 • м ³; D = 2 • м . На ТЭЦ-1 г. Улан-Удэ при температуре около - 40°С произошло замерзание воды как в сливном, так и выхлопном трубопроводах расширителя и он оказался закупоренным по всем отводящим потокам. При очередной продувке котлов произошло импульсивное нагружение, которое привело к мгновенному разрушению (взрыву) расширителя. Здесь проводится исследование напряженного состояния расширителя и определение внутреннего давления Р_разр в момент разрушения.

Напряженное состояние оболочек вращения описывается уравнением Лапласа [1]:

Р = - • t •

m 1

'

V R 2 R 1 7

где m = — - отношение главных напряжений; R 1 и R ₂ - главные радиусы кривизны оболоч- ^- 1

ки (дуги меридиана и нормального сечения); t - текущая толщина оболочки; р - внутреннее давление.

При определении предельной несущей способности сосуда следует учитывать работу металла корпуса в пластической области вплоть до разрушения. Для рассмотрения этого вопроса примем следующие упрощающие положения:

• 1.    Нагружение статическое. По ГОСТ 14249-89 [2], если сосуды работают при многократных статических нагрузках, но количество циклов нагружения от давления, стесненности температурных деформаций не превышает 10 циклов, такая нагрузка в расчетах на прочность условно считается однократной [3].

• 2.    Металл изотропный и в процессе нагружения интенсивность напряжения o i является функцией интенсивности деформаций s i , не зависящей от соотношения компонентов о 1 и

  о ₂ двухосного растяжения:

  
  
  
  

• 3.    Зависимость o i = f ( s ip ) можно аппроксимировать степенной функцией:

• 4.    Сосуд имеет идеальную форму цилиндра такой длины, что концевые эффекты на развитие пластических деформаций и разрушение его средней части влияния не оказывают. Стенки сосуда однородны по толщине.

• 5.    Расчетная температура стенки корпуса и днища из углеродистой стали не превышает 380⁰ C .

_     _ 2  _  _ , _ 2

^o i ^— У ^о 1 - ^о 1 "  ^о 2 + ^о 2 ,

si — sie + sip — ""+ + ” + J (s1 p - s 2 p  +(s1 p - s 3 p )2 + (s 2 p - s 3 p )2 ,

E 3

где o 1 , о ₂ - главные напряжения; о ₃ = 0; s 1 _p , s _{2 p} , s _{3 p} - пластические составляющие главных логарифмических деформаций.

О ^— A • ^s ip , где A и n - коэффициенты, постоянные для данного состояния металла, которые определяются экспериментальным путем.

Своеобразие работы тонкостенного сосуда заключается в том, что момент достижения максимального усилия X, разрывающего стенку сосуда, не совпадает с моментом достижения максимума давления Pmax внутри сосуда [1]. Для определения несущей способности сосуда важно установить, какое из этих двух предельных состояний наступает раньше.

о •

Давление внутри цилиндрического сосуда p — ——, где о - окружное напряжение.

R

Достижение максимума давления ( dp = 0 ) получается при условии, если d o dt dR

—¹ + — + — = 0.                             ⁽²⁾

о 1 t R

Для цилиндрического сосуда о 1 = 2 • о ₂. ; s _{2 p} = 0 ^ 2p ~ 0; s 1 _p = -s _{3 p} . Из уравнений (1)

имеем

о = ^|- • о;          s1 p

^do 1   _и^ds 1 p

----= n --, ^o 1          ^s 1 p

-^- • s ip , следовательно,

dt

— — d^s 3 p —

^{- ds} 1 p ,

dR

— — ds n.

R ^{1 p}

Подставляя выражения (3) в уравнение (2), получаем s 1 _p —^ n .

Таким образом, при этом значении окружной деформации стенки давление внутри цилиндрического сосуда достигает максимума:

• X — о 1 • l • t .

Из условия dX = 0 получаем уравнение do dt „

—1 + — — 0.

o 1      t

Из этого уравнения следует, что максимум разрывающего усилия Х имеет место при £ 1 p = n. Максимальное давление внутри цилиндрического сосуда достигается раньше (т.е. при меньших деформациях и напряжениях), чем наступает пластическая неустойчивость, связанная с максимумом усилия, приложенного в направлении наибольшего главного напряжения.

В соответствии с этим выразим величину условного расчетного напряжения при давлении p max ст _ 1 max м0 ст 1 расч                    , t 0

где Rо и tо - начальные значения радиуса кривизны и толщины стенки сосуда. Подставляя в t • <ст выражение (8) Pmax =---1 и значения

- n                               n

1 1 _ t о • e ^T, R _ R о • e 2 ,

соответствующие деформации

n

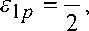
получим

ст

1 расч

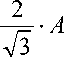
n

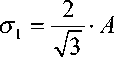
n

n

Ve•v3;

n

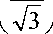
Таким образом, это выражение дает значение условного расчетного напряжения, характеризующего предельную несущую способность сосуда. Сопоставим это значение с пределом прочности сти, характеризующим предельную несущую способность материала в ус ловиях осевого растяжения.

Так как к началу образования шейки при осевом растяжении логарифмическая деформация £1 p _ n, то величину сти можно представить как сти = ст, • e -n, а так как Cтi _ Ст1 и £ip _ £1 p, то

[ X n

n

1 .

e /

Следовательно, для цилиндрического сосуда ст 1 расч "

Изменение этой величины в функции показателя степени упрочнения материала n, построенное в системе Mathcad [4], показано на рисунке 1 [2]:

ст _и : _ 500 • 10 6 • Pa ;

^ст 1 расч ⁽ n ) ^{: _}

W1

^{ст (} n )^{: _}

^ст 1 расч ^{( n} )

ст

n : _ 0,0.01..0.6.

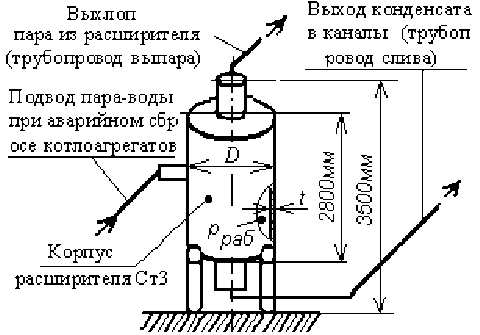
Рис.1. Схема обвязки и зависимость предельно возможной прочности сг(n) сосуда от показателя степени упрочнения n

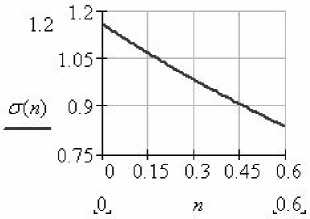
Как видно из рисунка 1 несущая способность цилиндрического сосуда может быть больше < т _м . и, если n <  0.26, или меньше o u при n >  0.26. Предел прочности материала сосуда o u = 500 -10⁶ • Pa .

Расчетное напряжение определяем из выражения:

^^{1 расч}    / I—\n + 1

⁽ Уз)

• О .

Толщина стенки сосуда определяется согласно ГОСТ [2] по формуле t >  t p + с .

Толщина стенки сосуда была равна t = 10 • мм . Прибавка с = 2 • мм к расчетной толщине стенки t p и делается для компенсации коррозии, вытяжки, штамповки и гибки и т.д. Расчетная толщина стенки сосуда t p по ГОСТ [2] определяется по формуле

p • D tp =------~----------.

² • ° l расч ‘ ^фp - p

Следовательно, с учетом сказанного для дальнейшего анализа можно принять t p = 8 • мм ; ф р = 1.0 - коэффициент прочности сварных соединений [2]; n : = 0 - наименьшее

_           О1 расч значение показателя степени упрочнения, при котором отношение —---- будет наиболь-ou

шим.

Из формулы (4) определяем внутреннее давление в расширителе

/   \ 1+ n   ^O u t p ^ф p

P =(Уз)       ____ разр D + tp

.

Р разр = 4.6 х 10⁶ Pa .

Таким образом, в момент разрушения сосуда предельное внутреннее давление равнялось Р разр = 46 • атт, и в этот момент внезапно произошло импульсивное нагружение расширителя давлением Р_ава р = 130 • атм при аварийном сбросе котлоагрегатов, которое превысило предельное давление для данного сосуда в 3 раза. Это вызвало взрывное разрушение расширителя периодической продувки котлов.

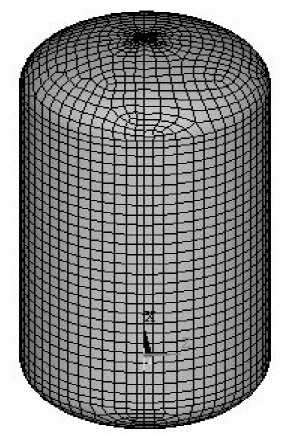
Рис.2. Конечно-элементная модель оболочки расширителя

Ограниченные возможности применения аналитических методов исследования приводят к необходимости использования программных комплексов, основой которых является метод конечных элементов (МКЭ). Примером системы, построенной на основе МКЭ, является пакет ANSYS, позволяющий решать задачи механики твердого деформируемого тела

Ниже представлены некоторые решения этой задачи.

Конечно-элементная модель (рис.2) содержит 3190 элементов SHELL93, которые используются для моделирования искривленных оболочек. Элемент имеет шесть степеней свободы в каждом узле, а также свойства больших перемещений и больших деформаций.

Приведенные результаты дают представление о реальном распределении напряжений в элементах оболочки расширителя (рис.3). При внутреннем давлении 38 атм напряжения в сосуде достигают предела прочности стали 500 МПа, что приводит его к разрушению. Расхождение результатов численного и аналитического решения составило 12%, что позволяет утверждать об адекватности КЭ-модели. Полученные результаты иллюстрируют эффективность использования инструмента численного анализа – МКЭ –для решения сложных реальных проблем и могут быть использованы для обоснования работоспособности теплоэнергетического оборудования.

Рис.3. Напряженно-деформированное состояние расширителя