Расчет надежности бесступенчатого механизма поворота промышленного трактора со следящей системой управления

В процессе разработки конструкции нового изделия для установления уровня его надежности и с целью получения информации об отказах, возникающих в изделии вследствие его конструктивных несовершенств, традиционно проводятся исследовательские испытания [1]. Получив информацию о фактических значениях показателей надежности изделия, разработчик либо убеждается в адекватности выбранных конструкторских решений, либо выявляет «слабые места» изделия и получает возможность их устранить.

Подготовка к проведению исследовательских испытаний среди прочих требует решения вопроса о требуемом объеме испытаний (числе испытываемых образцов, суммарной продолжительности испытаний в единицах наработки и числе серий испытаний) [2]. Определение объема испытаний – работа, связывающая надежность техники и экономику. С одной стороны, для повышения достоверности результатов испытаний нового изделия объём испытаний следует увеличить. С другой стороны, каждое проведённое испытание – это время и деньги, поэтому объём испытаний должен быть минимальным, поэтому часто на этапе проектирования ограничиваются исследовательскими испытаниями единственного опытного образца. Однако оценки показателей надежности носят вероятностный характер и при испытаниях опытного образца достоверность полученных оценок показателей надежности неприемлемо низкая.

В связи с этим акцент в оценке показателей надежности проектируемых изделий смещается от экспериментальных методов (методов, основанных на статистической обработке данных, получаемых при испытаниях или эксплуатации изделия) к расчетным методам [3–13]. Ведь дей- ствующие нормативные документы [2, 14] предусматривают как экспериментальные, так и расчетные методы оценки показателей надежности.

Определение уровня надежности бесступенчатого дифференциального механизма поворота со следящей системой управления (БДМПсССУ), достигнутого на стадиях проектирования и изготовления, выполнено расчетными методами по математической модели надежности (получена по результатам анализа структуры данного механизма и условий его работы) с использованием статистических данных интенсивностей отказов или наработок на отказ составных частей изделия, полученных в процессе испытаний приборов-аналогов.

Обычно для конкретных изделий устанавливают не более двух показателей надежности, на которые ориентированы проектанты при создании техники, в данном случае:

• 1)    наработка на отказ за 2000 часов работы машины должна быть не менее 1500 моточасов;

• 2)    срок службы до списания – не менее 5 лет.

Исходными данными при расчетах надежности любой восстанавливаемой системы являются:

• 1)    принципиальная схема системы с указанием элементов, входящих в систему;

• 2)    значения интенсивностей отказов и интенсивностей восстановления всех элементов системы при номинальных и фактических режимах ее работы.

В принципиальной схеме БДМПсССУД выделены 2 группы элементов [15]:

• –    первичные элементы: передача главная, ряд планетарный суммирующий, левая и правая бортовые передачи;

• –    элементы, состоящие из первичных:

• •    система смазки (состоит из фильтра, гидронасоса и рукава высокого давления (РВД));

• •    тормозная система следящей системы управления (состоит из гидропневмоаккумулятора (ГПА), 2 блоков управления тормозами (ручной тормоз и ножной тормоз), клапана зарядки ГПА и клапана давления, гидронасоса и РВД);

• •    гидросистема управления поворотом следящей системы управления (включает гидромотор, гидронасос, гидрораспределитель, электрогидрораспределитель, РВД и блок питания). Следует отметить, что отказы входящего в состав следящей системы управления (ССУ) электрооборудования (джойстик, микропроцессор, датчики, электрорадиоэлементы) – относительно редкие события по сравнению с отказами элементов гидравлической системы, гидростатического привода механизма поворота, механических элементов (редукторов), поэтому в расчетах надежности БДМПсССУ электрооборудование не рассматривается.

Интенсивности отказов элементов механизма постоянны и равны λ i , i = 1,2, …n, где n – число элементов в механизме (см. таблицу [16]).

Интенсивность восстановления i -го элемента БДМПсССУ определяется по выражению

Hi = 1/t в i , где tвi - среднее время восстановления i-го элемента изделия, определяемое группой сложности [17]: отказы элементов следящей системы управления (элементы тормозной системы и гидросистемы управления поворотом) относятся к отказам I группы с продолжительностью устранения 2 ч (µI = 0,5 ч– 1); отказы элементов БДМП относятся к отказам II группы сложности с продолжительностью устранения 8 ч (µII = 0,125 ч–1).

Проведем расчет надежности с учетом следующих допущений:

• 1.    Отказом разрабатываемого БДМПсССУ считается: потеря герметичности элементов гидравлической системы гидростатического привода механизма поворота; подтекание масла через соединения и уплотнения с каплеобразованием; контактные разрушения зубьев; поломка зубьев; заедание передачи; повреждение подшипников; повреждение (разрушение) нагруженных деталей и узлов (разрыв шлангов высокого давления, повреждение гидрооборудования и т. п.).

• 2.    Каждый элемент может находиться в двух несовместных состояниях: работоспособном и неработоспособном.

• 3.    Распределение наработки до отказа и времени восстановления отдельных элементов является экспоненциальным, то есть процесс функционирования изделия является стационарным, без последействия (благодаря использованию блокировок, предохранительных клапанов и независимых источников питания отказ одного элемента не провоцирует возникновение отказов других элементов), и ординарным.

• 4.    Надежность средств контроля идеальна, отказавшие элементы начинают восстанавливать немедленно; отсутствуют ограничения на число восстановлений; на интервале восстановления отказы не возникают (это обеспечивается правильной организацией системы технического обслуживания и ремонта изделия).

Интенсивность отказов элементов механизма

№ п/п	Блок	Элемент	Лг10-6, ч –1
1	Передача главная, ряд планетарный суммирующий, передача бортовая левая, передача бортовая правая	–	0,2
2	Система смазки	фильтр	0,3
		гидронасос	8,74
		рукава РВД	3,93
3	Следящая система управления	гидропневмоаккумулятор (ГПА)	6,1
		блок управления тормозами (ручной тормоз)	3,55
		блок управления тормозами (ножной тормоз)	3,55
		клапан давления	5,6
		клапан зарядки ГПА	5,6
		гидронасос	8,74
		рукава РВД	3,93
		гидромотор	1,8
		гидронасос	8,74
		гидрораспределитель	3,55
		электрогидрораспределитель	3,55
		блок питания	6,1
		рукава РВД	3,93

Теперь по имеющимся сведениям о надежности элементов и о связях между элементами, а также с учетом принятых допущений проведем расчет надежности БДМПсССУ.

Начнем с расчета величины наработки на отказ БДМПсССУ – показателя безотказности восстанавливаемого изделия, который определяет среднее время между соседними отказами.

Согласно выражению

t

Т н ( t ) = J K г ( t ). ,                                                                                  (1)

расчет наработки на отказ БДМПсССУ требует определения комплексного показателя надежности – функции готовности K _г ( t ) . Одним из методов определения функции готовности является метод дифференциальных уравнений [5].

Для использования этого метода составлена математическая модель БДМПсССУ в виде графа состояний (множества следующих состояний системы, в которых она может находиться при отказах и восстановлениях: 0 – работоспособное состояние БДМПсССУ; 1 – состояние отказа БДМПсССУ из-за отказа ССУ; 2 – состояние отказа БДМПсССУ из-за отказа БДМП) (рис. 1).

На рис. 1 указаны следующие величины: λ 1 – интенсивность отказов ССУ (λ 1 = (2·8,74 + + 2·3,93 + 2·5,6 + 4·3,55 + 2·6,1 + 1,8)·10^–6 = 64,74·10^–6 ч^–1); λ 2 – интенсивность отказов БДМП, включающей главную передачу, планетарный ряд, левую и правую бортовые передачи и систему смазки (λ 2 = (4·0,2 + 0,3 + 8,74 + 3,93)·10^–6 = 13,77·10^–6 ч^–1); µ I – интенсивность восстановления каждого из 13 элементов ССУ (µ I =0,5 ч^–1); µ II – интенсивность восстановления каждого из 7 элементов БДМП (µ II = 0,125 ч^–1 ).

Чтобы предельно уменьшить затраты труда на расчет функции готовности по графу состояний (см. рис. 1), последний укрупнен объединением состояний 1 и 2 в одно состояние 12 (рис. 2).

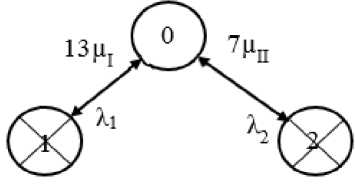
Рис. 1. Граф состояний БДМПсССУ

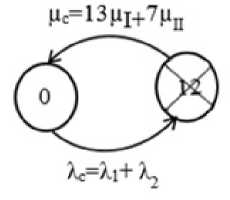
Рис. 2. Укрупненный граф состояний БДМПсССУ

Система дифференциальных уравнений для вероятностей состояний (уравнения Колмогоро- ва), составленная по графу (см. рис. 2), имеет вид

/( ) = A P> (t) + ЦcP (t), . P,2(t ) = XcP, (t) — Цс P, (t)

С учетом начальных условий Р0(0) = 1, Р12(0) = 0 уравнения (2) записаны в операторной форме

/ s^P 0 ⁽ s ^{)- 1} = — ^Xc ^P 0 ⁽ s ) ⁺ Ц c ^P 12 ⁽ s ) , , sP ⁽ s ) = X c PP ⁽ s ^)- Ц с P 2 ^{( s} )

Решение (3) в операторной форме имеет вид

К г( s) = P, (s )=

Ac + s s (s + (2c + ^c))

µc

² c ^{+ p} _c

•- +

s

λ c

2c + ^c

s+(2c + McY

Выражению (4) во временной форме соответствует функция готовности вида

² c     e -( Л :⁺ Цс) t

2 _c + A c

Кг( t) = P, (t )= V^L-2c + A

• а с учетом числовых значений λ с и µ с

  Кг(t) = P0 (t)= 0,9999894 + 0,0000106 • e-7,3750785 • t

Функция готовности (6) не учитывает нагрузок, которые возникают при эксплуатации БДМПсССУ в составе подвижного объекта. Влияние эксплуатационных нагрузок легко учесть введением поправочного коэффициента эксплуатации а , который показывает, во сколько раз возрастают интенсивности отказов элементов изделия. Так, для элементов автомобильной аппаратуры а = 40 [18, 19]. С учетом увеличения интенсивности отказов элементов в 40 раз ( λ с = 3,14·10^–4 (ч^–1)) из (5) получим

К г (t) = P0 (t) = 0,9995744 + 0,0004256 • e "7,37814 • t.                                     (7)

По выражениям (1) и (7) проведен следующий расчет наработки на отказ БДМПсССУ

Т н (2000 ) = J (0,9995744 + 0,0004256 • e - 7, ³⁷⁸¹⁴ ' t ) dt = 0,9995744 • 2000 +

+ 0,0004256 • e-7,37814 '2000 • (-7,37814) = 1999, т. е. наработка на отказ за 2000 часов составляет 1999 моточасов, что удовлетворяет требованиям задания.

Долговечность БДМПсССУ оценим величиной срока службы. Срок службы изделия – календарная продолжительность эксплуатации от начала эксплуатации изделия до его списания, обусловленного предельным состоянием [20]. Причем под предельным состоянием разработанного БДМПсССУ будем считать состояние, при котором его ремонт становится экономически нецелесообразным ввиду его низкой надежности.

Согласно (7) через 5 лет (43800 ч) после начала эксплуатации коэффициент готовности составит

Кг(43800) =0,99957,

• т. е. за плановый срок службы БДМПсССУ (5 лет) с установленной системой технического обслуживания и ремонтов не наступит предельное состояние изделия, определяемое как состояние, при котором дальнейшая эксплуатация изделия недопустима/нецелесообразна из-за не устраненных по тем или иным причинам нарушений работоспособности, а значит срок службы до списания БДМПсССУ – не менее 5 лет.

Особенность приведенных расчетов показателей надежности БДМПсССУ в том, что в них сделан акцент на конструктивные, а не на производственные и эксплуатационные отказы. Это позволяет убедиться в грамотности принятых на этапе проектирования решений, в том числе решения об унификации и стандартизации деталей, узлов, решения об использовании высоконадежных элементов и узлов. Это оправдано не только повышением надежности изделия, но и сокращением его стоимости.

Работа выполнялась при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках комплексного проекта по созданию высокотехнологичного производства «Разработка бесступенчатого дифференциального механизма поворота со следящей системой управления для внедорожных и дорожно-строительных машин нового поколения» по соглашению № 074-11-2018-006 от 31.05.2018 г. между Министерством науки и высшего образования Российской Федерации и Обществом с ограниченной ответственностью Производственная компания «Ходовые системы» в кооперации с головным исполнителем НИОКТР – Федеральным государственным автономным образовательным учреждением высшего образования «Южно-Уральский государственный университет (национальный исследовательский университет)».