Расчет напряженно-деформированного состояния сложно армированных металлокомпозитных оболочек в условиях установившейся ползучести

Настоящая работа продолжает исследования автора [1, 2], посвященные расчету металлокомпозитных изгибаемых пластин и искривленных панелей со сложными структурами армирования, работающих в условиях установившейся ползучести. В инженерной практике, помимо пластин и искривленных панелей, в качестве тонкостенных элементов конструкций широко используются оболочки большой кривизны. В теории оболочек известен тот факт, что пологие оболочки (искривленные панели) при нагружении в поперечном направлении ведут себя подобно изгибаемым пластинам, а оболочки большой кривизны, в которых основное напряженное состояние является безмоментным, — подобно пластинам, нагруженным в своей плоскости. В связи с этим результаты расчетов искривленных панелей не всегда могут быть экстраполированы и на оболочки большой кривизны. Поэтому актуальной является

проблема расчета металлокомпозитных оболочечных элементов при установившейся ползучести всех компонент композиции.

Данное исследование содержит: постановку задачи определения напряженно-деформированного состояния армированных металлокомпозитных оболочек большой кривизны, работающих в условиях установившейся ползучести; анализ соответствующей граничной задачи; обсуждение методов ее линеаризации и численного интегрирования; изучение на примере цилиндрических оболочек деформативности таких тонкостенных конструкций в зависимости от типа закрепления их кромок, структуры армирования и геометрических размеров.

2.    Исходные уравнения и граничные условия

Рассмотрим деформирование тонкой оболочки переменной толщины 2 H , подчиняющейся гипотезам Кирхгофа-Лява и состоящей из изотропной металлической матрицы и внедренной в нее тонковолокнистой однородной арматуры (металлических проволок, возможно, различной физической природы) постоянного или переменного поперечного сечения (допустимость гипотез Кирхгофа-Лява при расчете установившейся ползучести тонкостенных элементов конструкций обоснована в [3]). Используем предположения: к рассматриваемому моменту времени деформации ползучести получили настолько значительное развитие, что по сравнению с ними можно пренебречь начальными упругими и пластическим деформациями [3]; оболочка по толщине имеет регулярную и квазиоднородную структуру; перемещения малы, то есть принимаем геометрически линейную теорию оболочек; температура T однородна по толщине конструкции и известна из решения соответствующей задачи теплопроводности [4].

С оболочкой связана ортогональная система координат x x ₂ z ; поверхность x x ₂ ( z = 0) совмещена со срединной поверхностью конструкции до деформирования, причем координатные линии x ₁, x ₂ совпадают с линиями главных кривизн этой поверхности, а z определяет расстояние от выбранной точки оболочки до срединной поверхности. Конструкция армирована N семействами волокон (проволок), которые уложены по поверхностям, эквидистантным срединной поверхности (эквидистантное армирование), или по поверхностям, расстояния до которых от срединной поверхности по оси z изменяются пропорционально изменению H ( x ₁, x ₂) (неэквидистантное армирование).

Для формулировки задачи деформирования в условиях установившейся ползучести армированных оболочек используем общеизвестные выражения [3, 5]:

• - уравнения равновесия

( a f ) - A. F + ( AF. ) + A Fi + AAQi I Ri + A Aq = 0, у j ii J i j , i jj у i ji j j i , j ij 1 2 ^^i i 12 i I ?

( AM\ i - ^A 1 M . + ( A i M ji ) , j + AM - A 1 AQ + A 1 A 2 m , = 0,

( A Q), + ( A Й 2 ) , ₂ - AA ( F 1 I R + F 22 1 R 2 ) + A A 2 q. = 0,

F - M. ,I R - Fa + Mi /R Ra = 0     (j = 3 - i, i = 1,2);

12        21      2       21        12      1

- соотношения, связывающие скорости мембранных деформаций e j и параметров искривления к j срединной поверхности оболочки со скоростями перемещений и i , w точек этой поверхности:

ё_й = A;¹ «. ,+ ( A i A 2 ) - 1 A Л + R - w ,

2 e i2 = 2 6 2i = A i A 21 ( U tJ A ) ,2 + A 2 A ^- ( ^ 2/ A 2 )_д ,

У=- Г ( w J A-AR ) , . - ( A i A ) ^{- 1} A^ w j A- j R)   ( j = 3 - i ,   i = 1,2 ) ,   (2)

^K 12 = ^K 21 =^{-( A} 1 A 2 ) ( w ,12 ^{- A} 1,2 w ,1/ A i ^- A ,1 w ,2/ A ) +

^{+ R} 1 ⁽ u 1,2 / ^A 2 ^{- A} 1,2 ^U 1 К ^A 1 ^A 2 ^{)) + R} 2 ⁽ u 2,1/ ^A 1 ^- A 2,1 ^Ut2 /{ ^A 1 A 2 ) ) ;

– определяющие соотношения, связывающие мембранные усилия F_ij и моменты M _j в оболочке со скоростями деформаций ё_у и параметров K j :

22                22

F = У УВЛ-В + B ,к.),    M.. = У У( D ,ё, + C ж Л G, j = 1,2),        (3)

j             jnl nl jnl nl , j             jnl nl jnl nl ,,, n=1 l=1                                                    n=1 l=1

где коэффициенты A _jnl , B _jnl , C _jnl , D _jnl в рамках теории течения установившейся ползучести [3], используемой в настоящем исследовании, нелинейно зависят от ё ml и к ml , параметров армирования, температуры T ( x 1 , x ₂), толщины оболочки и механических характеристик установившейся ползучести материалов компонент композиции. Так как тонкая оболочка подчиняется гипотезам Кирхгофа–Лява, то для определения A _jnl , B _jnl , C _jnl , D _jnl можно использовать соотношения, полученные в [1] (здесь не приводятся в силу их громоздкости).

В случае неэквидистантного армирования тонкой оболочки непрерывными волокнами постоянного поперечного сечения между параметрами армирования существует связь, приближенно определяемая равенством [6]

( HA ₂ го k cos v _k ) , 1 + ( HA 1 to _k sin v _k ) ,₂ = 0    ( k = 1, 2, ..., N ) ,

которое при эквидистантном армировании редуцируется в равенство, получающееся из (4) формальным заданием H = 1.

К уравнениям и соотношениям (1)–(3) необходимо добавить общеизвестные граничные условия на кромках оболочки [5] (не будем их здесь приводить, так как они весьма разнообразны). На той части кромки (обозначим ее Г _k ), где волокна к -го семейства, имеющие постоянные поперечные сечения, входят в конструкцию, следует задать краевые условия [6]

ш к ( Г к ) = _Ю о к ( к = 1,2,..., N ) ,

необходимые для однозначного интегрирования уравнений (4).

Доопределим в уравнениях и соотношениях (1)–(5) принятые обозначения: A , R — параметры Ламе и главные радиусы кривизны срединной поверхности оболочки соответственно; Q — перерезывающие усилия; q , qz — приведенные распределенные нагрузки в направлениях x ,z соответственно; m — приведенные распределенные изгибающие моменты, вызванные внешними нагрузками; wv, ui — скорость прогиба и скорости перемещений точек срединной поверхности оболочки, соответственно, в направлениях xi (1' = 1,2) в условиях установившейся ползучести; ш к, V к — интенсивность и угол армирования волокнами к-го семейства (у к отсчитывается от направления координатной линии X’); «0k — заданная на кромке Гk функция; нижний индекс после запятой означает частное дифференцирование по соответствующей переменной xi ; точка над функцией означает частную производную от этой функции по времени.

3.    Система разрешающих уравнений

Для получения системы разрешающих уравнений деформирования сложно армированных оболочек, работающих при установившейся ползучести, и соответствующих системе статических граничных условий в скоростях прогиба * и скоростях тангенциальных перемещений u i необходимо выражения для ё_у . к _у из (2) подставить в соотношения (3), последние — в уравнения равновесия (1) и граничные условия, а затем исключить из рассмотрения поперечные силы Q_i . Тогда три уравнения равновесия примут разрешающий вид (при этом последнее равенство в (1) выполняется приближенно):

(a, P.)., - a,,> P  +(ap,,),,+A P + R- [(a,м.), - a,., м*+

+ ( 4 мД + A W- A 1 A 2 ( q , + R - ’ m )     (j = з - i. i = 1.2).

S{A   (4Mii), i=1 v L               .

- A,.,м,,+(am,,)

⁺ A i . j ^M j-

} - A i A 2 £ R 'P ,, ' . i                     i = 1

= ^- A i A 2 q z - ( A 2 m i ) .’ - ( A i ^m 2 ) ,2

( j = 3 - i ).

где операторы P , и M , имеют смысл поперечных сил и моментов соответственно:

u i . u 2 . * ) = ^ { A_yu l =’ ¹

A, - ’ i , + ( A A )- ’ A й + R ^{- l} * 1 - B_in , Г A, -’ ( A, - ’ tv, - l l . l \ i 2 / l . m m l                   yll I l \ l       . l

- R-’ U ) + (AA )-’ A m ( A - wm - R - u )1! + An 2 Г AA"’ ( A-’ i) + AA-’ x l l j l у i 2 / l. m у m    . m       m m / _ I       j ’2     i 2 у i ’ / 2       2 ’

x ( A ■' uq ),

- 2 B , i2

⁽ A i A 2 )   A i.2^!ti

( A i A 2 ) - ¹ ( * ,2 - A-’ 4.2 > W , - A 2 ^{- i} A 2,i * ;, ) - Ri' ( A2'U‘ i,2 -

) - R 2 - ’ ( A ’”’■'2.I

⁽ A i A 2 )   A 2.i u ^t 2

^M ij ( ^lti . ^lt2 . ^w ) = E { D ijll l =i ^V

A - ’ it.. + ( A A )"’ A uii + R ."' t V 1 - C_m . Г A " ' ( A .-’ Vv. - l      l . l      \ i 2 /          l . m m l                   ijll I l \ l       . l

- R;’ i ) +(AA )-’ A J A - TV„ - R т’йт )1) + DiiX J AA2■’ (A-' II,) + A2A-’ x l l j l у i 2 /         l. ^н ^    ^н     . ^н          ^н    ^h j I | Ij ’2 i 2 ^ i ’ ' 2          2 i

x ( A ₂ ’ u₂ )

,1

-2C ij12

⁽ A i A 2 )   ( w^ .’2 - A i ’ A i.2 "w .’ - A 2’ A 2 .i "w .2 ) - R i’ ( A 2 ’ ^Zti.2 -

⁽ A i A 2 )   A i.2 u i ) ^R 2 ( A i ^Zt2.i    ⁽ A i A 2 ) A 2.i ^U 2

m = 3 - 1 .    i . j = i. 2 ) .

На кромке x i = const. согласно теории установившейся ползучести тонких оболочек, граничные условия могут быть заданы в виде линейных комбинаций следующих величин [3, 5]:

– статические граничные условия

^P ii (ii i . ut 2 . tv ) = F i ⁰. ^M ₁₇ (li ’ . ui 2 . tv ) = M i, .

P „ ( «_р « 2 , V ) + R ^-' M j ( « 1 , « 2 , V ) = F j ,                                                  (8)

(AA)-1 [(A,M,),,-A.,Mj.+(AM,),j+ A,,jM„]+A-1M„ = Q -m,   (j = 3-i), где Fi,, M^, Fij, Qi — известные на этой кромке x4 = const силовые факторы ( Qi0 — приведенная сила Кирхгофа); в равенствах (8) также нужно учесть выражения (7); – кинематические граничные условия itl = it0 (l = 1,2),    av = V0,    - A,-1 av,,+ R-1 «,=90,

где it 0 , av ⁰, 9 ⁰ — заданные на кромке функции (скорости тангенциальных перемещений, прогиба и углов поворотов);

• – смешанные граничные условия, которые могут включать величины, входящие как в (8), так и в (9).

4.    Модельная задача

Если контур, ограничивающий отсчетную поверхность оболочки, не совпадает с одной из координатных линий x , = const, статические и кинематические граничные условия, записанные в скоростях перемещений, существенно усложняются [5] по сравнению с (8), (9). Однако этот случай не имеет принципиального значения для настоящего исследования, поэтому здесь не рассматривается.

При условии, что толщина оболочки 2 H и траектории армирования (то есть углы у k ) известны, из решения краевой задачи (4), (5) определяется to k — интенсивность армирования волокнами k -го семейства. Краевые задачи для линейных уравнений в частных производных первого порядка (4) хорошо изучены (см. [7]), поэтому не будем останавливаться на обсуждении этого вопроса, а отметим лишь, что уравнение (4) имеет действительные характеристики, совпадающие с траекториями армирования k -го семейства. Зная функции у k , to _k , H , в оболочке можно найти стационарное температурное поле T ( x 1 , x ₂ ) (соответствующие граничные задачи сформулированы и проанализированы, например, в [4]), после чего три разрешающих уравнения равновесия (6) с учетом (7) станут замкнутыми относительно трех функций « 1 , it₂ , av . Этой системе квазилинейных дифференциальных уравнений эллиптического типа соответствуют граничные условия — нелинейные (8) (с учетом (7)), линейные (9) или их комбинации.

Основная трудность, возникающая при решении граничной задачи деформирования сложно армированных оболочек в условиях установившейся ползучести, заключается в ее существенной нелинейности. Для линеаризации сформулированной задачи можно использовать итерационный процесс, основанный на применении метода секущего модуля [3] (наряду с описанием процесса вычислений здесь также доказывается сходимость метода); адаптация метода секущего модуля к расчету тонкостенных металлокомпозитных элементов конструкций подробно изложена в [1]. Так как на каждой итерации вычислительного процесса приходится решать линейную граничную задачу, формально схожую с задачей упругого деформирования слоистых анизотропных и неоднородных оболочек со слоями переменной толщины [5, 8], то для интегрирования такой граничной задачи можно использовать или уже известные и хорошо разработанные конечно-разностные схемы, или метод конечных элементов, или другие приближенные вариационные методы.

З а м е ч а н и е 1. Получив из решения граничной задачи скорости прогиба av и тангенциальных перемещений точек отсчетной поверхности it 1 , it₂ , по формулам (2), (3)

можно определить внутренние силовые факторы F_ij , M_ij в оболочке (а по формулам (1.2), (1.6)-(1.9), (1.17)-(1.19) из [1] — напряженное состояние ст ij во всех фазовых материалах и в композиции в целом), работающей в условиях установившейся ползучести. Если помимо этого в конструкции для внутренних силовых факторов F j , M ij известно и начальное состояние, порождаемое усредненными напряжениями CT j (см. (1.2), (1.3) в [9]), которое можно определить, например, методами, изложенными в [5, 8], то решение задачи неустановившейся ползучести на первой ее стадии можно получить приближенно, используя методику, предложенную в [3]. Для этого п редс т авим текущее состояние для внутренних силовых факторов в оболочке F_ij , M_ij и соответствующее ему текущее усредненное напряженное состояние в композиции ст j в виде: F j = ( 1 ^-т ( t ) ) Ё_у ^+т ( t ) F ij , ^M j = ( 1 ^-т ( t ) ) M j +^T ( t ) M j , ^ст j .= ( l ^-т ( t ) ) ^ст у +т ( t ) ^ст ij ( i , j = 1, 2 ) , где т ( t ) — монотонная функция времени t , возрастающая от значения т = 0 в начальный момент времени t = 0 до т = 1 при t ^го . Функцию т ( t ) можно определить, исходя из экстремальных принципов теории ползучести (см. § 34 в [3]). В случае изотропных оболочек реализация такого подхода не вызывает особых трудностей, а в случае тонких конструкций со сложными структурами армирования требует проведения дополнительного, более тщательного исследования, выходящего за рамки настоящей работы.

Определив из граничной задачи (6)-(9) скорости перемещений U 1 , ui₂ , w , по формулам (2) можем вычислить скорости деформаций ползучести в любой точке оболочки, а затем и максимальные значения интенсивности скоростей деформаций. Знание последних позволяет в ряде случаев оценить, допустима ли нормальная эксплуатация тонкостенной металлокомпозитной конструкции с заданной структурой армирования в условиях длительного термосилового нагружения, так как для целого ряда изделий предельная скорость деформаций в условиях установившейся ползучести строго регламентирована [10]. Кроме того, знание скоростей деформаций установившейся ползучести дает возможность на базе деформационной теории [11 и др.] или энергетического критерия длительной прочности [12 и др.] в первом приближении оценить и длительность времени до начала разрушения металлокомпозитной оболочки. Для этого достаточно пренебречь третьей стадией ползучести (стадией предразрушения) материалов компонент композиции, поскольку ее продолжительность, как правило, пренебрежимо мала по сравнению с общим временем эксплуатации конструкции в условиях длительного нагружения (именно так обычно и поступают исследователи, оценивающие долговечность конструкций расчетными методами), и рассматривать только первую и вторую стадии ползучести с учетом соображений, изложенных в Замечании 1.

В качестве модельной задачи рассмотрим осесимметричное деформирование тонкой цилиндрической круговой замкнутой оболочки, имеющей длину L, радиус R, параметры Ламе A1 = A = 1, 1(R1 = 0, R2 = R и работающей в условиях установившейся ползучести. Конструкция осесимметрично нагрета ( T = T (х1)) и нагружена внутренним или внешним давлением qz = const. Нагрузки в окружном направлении x2 отсутствуют (q2 = 0, m2 = 0, F10 = 0). Армирование осуществляется четным количеством семейств волокон (N = 2K ) по меридионально-симметричным траекториям ( ^ 2k-1(x1) = -у2k (x1), Ю2k-1(x1) = ®2к (xi), 1 ^ k ^ K ).

В силу осесимметричного термосилового нагружения оболочки, отсутствия нагрузок в окружном направлении и меридионально-симметричного ее армирования тождественно равны нулю функции й₂, ё ₁₂, к ₁₂, M ₁₂, F ₁₂ и все производные по переменной x ₂ в соотношениях (1), (2), (4), (6)-(9), поэтому уравнения равновесия (1) при q 1 = 0, m 1 = 0 редуцируются в систему двух равенств (при этом из третьего уравнения (1) исключается поперечная сила Q 1 за счет второго соотношения (1) при i = 1):

F» = 0,     M 1'1 - F 22 R = - q , ,

где штрих означает обычную производную по продольной координате x ₁ . Остальные уравнения в (1) выполняются тождественно.

Из первого уравнения (10) следует:

F 11 ( x ) = F 10 = const,

где F ₁⁰₁ — заданное осевое усилие на одной из кромок оболочки.

Воспользуемся соотношениями (2), (3) и исключим из рассмотрения и ' .

В результате второе уравнение (10) преобразуем к виду

M 1'1 - a 11 M 11 + a ₁₂ w = - q_z + b 1 .

К этому уравнению добавим выражение для M ₁₁ из (3) с учетом (2), которое перепишем так:

a ₂₁ w " - a ₂₂ w + M 11 = b ₂.

Здесь:

a11(x1, w , w) = R D(A1111B 2211 - B1111 A 2211), a12 ( x1, W , W ) = D R IB2211 ( A1111D1122 - D1111A1122 ) + A2211 ( A1122 C1111 - D1122 B1111

( x1, w , w) = D, b2 ( x1, TV'', TV ) = D1111F10, D = A1111C1111 - D1111B1111.

b ( X 1 , TV ", TV ) = D ^{- 1} R ^{- 1} ( A 2211 C 1111 - B 2211 D 1111 ) F 10 , ^a 22 ^{( x} 1 , w^ , w ^V ) = ^{R  (} A 1111 D 1122 ^- D 1111 A 1122 ) ,

На кромках цилиндрической оболочки имеем: – при шарнирном опирании

M 11 ( X 1 ) = 0, t v ( X 1 ) = 0 ( X 1 = x „ , X 1 = x „, x „- x , = L );                              (15)

– в случае жесткого защемления

T V ( x 1 ) = 0, tv' ( x 1 ) = 0 ( x 1 = x , , x 1 = x „),

где x , , x ,, — осевая координата левой и правой кромок оболочки соответственно (граничные условия (11), (15), (16) соответствуют случаю, когда одна из кромок оболочки не допускает смещения в осевом направлении x ₁ , а другая кромка может смещаться в этом направлении). Если оболочка нагрета, нагружена и армирована симметрично относительно центрального поперечного сечения x 1 = x , + L / 2, то в этом сечении выполняются равенства:

M 11 ( х 1 ) = 0,    w ' ( х 1 ) = 0    ( x 1 = x , + L /2).

Для численного интегрирования двухточечной граничной задачи производные по x ₁ в соответствующей ей системе уравнений (12), (13) и граничных условиях (15), (16) (или (17)) аппроксимируем трехточечными конечно-разностными аналогами на равномерной по x ₁ сетке. Уравнения (12), (13) при этом линеаризуем по методу секущего модуля [1], то есть коэффициенты а_у и свободные члены b i ( i , j = 1, 2) в них предполагаем известными из решения на предыдущей итерации. Граничную задачу для конечно-разностного аналога системы (12), (13) решаем методом матричной прогонки [13], в качестве неизвестных при этом выступают узловые значения функций M 11 , w (многочисленные расчеты показали, что достаточное условие устойчивости метода прогонки [13] всегда выполняется).

После того как на данной итерации находим узловые значения функций M 11 , w , из уравнения (13) в узлах сетки вычисляем вторую производную w" , затем по формулам (14) с учетом (2) и выражений для коэффициентов A _jkl , B _jkl , C _jkl , D _jkl , подробно рассмотренных в [1], определяем, согласно методу секущего модуля, новые приближения узловых значений коэффициентов a j и свободных членов b i (i, j , k , l = 1, 2) в системе (12), (13). Затем описанную процедуру численного интегрирования линеаризованной системы (12), (13) повторяем на новой итерации. Итерационный процесс продолжаем до тех пор, пока не будет достигнута заданная точность (на практике расчеты прекращались при выполнении условия || w n ₊₁ - w J _c/|| w n +J | _c <  10 - 4 , где n — номер итерации, а по координате x ₁ вводился 401 узел на равномерной сетке).

5.    Обсуждение результатов расчетов

В качестве примера исследуем установившуюся ползучесть замкнутых круговых цилиндрических оболочек радиусом R = 0,5 м и длиной L . Толщина оболочек может быть постоянной (2 H ( x 1 ) = 2 H , = const) или переменной и определяется формулой

2 H ( x 1 ) = 2 H , 5 + п ( 1 - 5 ) H , sin ( n x 1 / L ) ,   0 <  x 1 <  L .

При задании толщины тонкой цилиндрической оболочки в виде (18) и постоянстве плотностей армирования ( to _k = const, k = 1,2,..., N ) расход материалов компонент композиции в рамках точности используемой теории тонких кирхгофовских оболочек будет такой же, как и в оболочках постоянной толщины 2 H , . При значениях параметра 0 <  5 <  1 из (18) следует, что толщина оболочки на кромках x 1 = 0, x 1 = L меньше, чем в центральном сечении x 1 = L / 2; при 5 = 1 получаем оболочку постоянной толщины

• 2 H . ; при 5 >  1 толщина оболочки на кромках больше, чем в центральном сечении. В расчетах принято 2 H , = 2 см .

На кромках X 1 = 0, x 1 = L оболочки могут быть шарнирно оперты или жестко защемлены (в осевом направлении х 1 кромки смещаются свободно, то есть F 10 = 0 ; см. (11)). Конструкции нагружены внутренним давлением интенсивности q z = 5 МПа ( q 1 = 0).

Рассматриваем металлокомпозитные оболочки, изготовленные из твердой меди (Cu) или алюминиевого сплава АМг3, меридионально-симметрично армированные ( V 1 ( x 1 ) = -V ₂ ( x 1 ) = V = const, to , ( x 1 ) = to ₂ ( x 1 ) = const) двумя ( N = 2 , K = 1) семействами стальной проволоки У8А.

При температуре T * 200 ° C законы установившейся ползучести для этих материалов имеют вид:

Cu [14]:     Ё = B о m ч ^{- 1}, B = 3,65 • 10 ^{- 10}(МПа) ^- m • ч ^{- 1}, m = 1,6;

АМг3 [15]: Ё = exp ( - K + во ) ч ^{- 1},    K = 12,2,    р = 0,0673 (МПа) ^{- 1};          (19)

У8А [16]: Ё = B о ^m ч ^{- 1}, B = 1,054 • 10 ^{- 84}(МПа) ^{- m} • ч ^{- 1}, m = 24,982.

Согласно [1] аппроксимируем эти зависимости двухзвенными кусочно-линейными функциями

' Це,             0 <Ё <ЁР

О1 + B2 (ё -Ё1), Ё > Ё1

со следующими характеристиками для выбранных материалов компонент композиции

Cu:     B 1 = 4,754 •Ю ¹³Па • ч, B ₂ = 1,797 •Ю ¹³Па • ч, о 1 = 1,136ГПа,

Ё 1 = 2,39•Ю ^{- 5} ч ^{- 1};

АМг3: B = 940,97 ГПа • ч,     В₂ = 209,73 ГПа • ч,    о, = 30,194 МПа,

121   (21)

Ё 1 = 3,209 •Ю ^{- 5} ч ^{- 1};

• У8А: B 1 = 1,61Ы0¹⁵ Па • ч, B ₂ = 1,257 •Ю ¹² Па • ч, о 1 = 1,466ГПа,

0.E+00 2.E-05 4.E-05 6.E-05 8.E-05 1.E-04 § , ч - ¹

Ё 1 = 9,097 •Ю ^{- 7} ч ^{- 1}.

Параметры (21) определены на основании зависимостей (19) методом наименьших квадратов на интервале 0 <Ё <  10 - 4 ч ^{- 1}, при этом варьировались величины о 1 , Ё 1 . Значения (21) можно несколько уточнить, если в (20) варьировать параметры о 1 , Ё 1 , B ₂. На рисунке 1 сплошные кривые 1 , 2 , 3 характеризуют зависимости (19) для материалов Cu, У8А, АМг3 соответственно; двухзвенные же штриховые ломаные 1’ , 2’ , 3’ характеризуют аппроксимации (20), (21) для тех же материалов. В силу выбранного масштаба по оси ординат линия 3’ визуально практически не отличается от кривой 3 . Сравнение кривых 1 , 2 , 3 и 1’ , 2’ , 3’ показывает, что зависимость (20) с параметрами (21) удовлетворительно аппроксимирует законы установившейся ползучести (19), поэтому при решении рассматриваемой задачи для вычисления коэффициентов A_ijml , B_ijml , C_ijml , D_ijml в определяющих уравнениях (3) (и в (14)) можно обоснованно использовать методику, разработанную в [1]. Отметим, что для материалов компонент

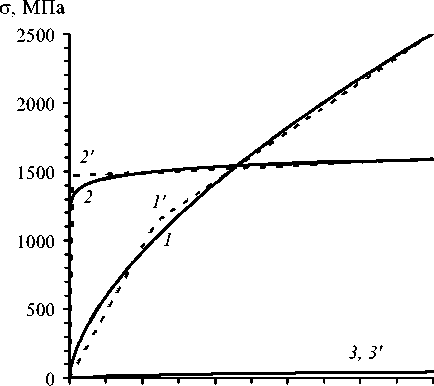
Рис. 1. Кривые установившейся ползучести материалов компонент композиции и их аппроксимация двухзвенными ломаными композиции в качестве начальных приближений секущих модулей на первой итерации принимались значения B1 из (21).

Так как армирование предполагается однородным ( у k = const, to _k = const), то для цилиндрической оболочки условие постоянства поперечных сечений волокон (4) выполняется тождественно (случай эквидистантного армирования). В расчетах примем to 1 +to ₂ = 0,7 ( to 1 = to ₂ = 0,35), что на практике соответствует удельной суммарной плотности армирования, близкой к предельно допустимой. При этом для любых углов армирования ψ общий расход арматуры в цилиндрических оболочках фиксированной длины L будет один и тот же.

На рисунке 2 изображены зависимости w, (у) = max |w(x; у)| для двух 0< x, < L композиций: АМг3–У8А и Cu–У8А. Кривые 1–4 получены для шарнирно закрепленных на кромках оболочек (см. (15)), а 1’–4’ — для конструкций с жестко защемленными кромками (см. (16)). Линии 1, 1’ и 4, 4’ на рисунке 2, а, а также 3, 3’ и 4, 4’ на рисунке 2, б визуально почти не отличаются. Кривые 1, 1’, 2, 2’ соответствуют металлокомпозитным оболочкам, а горизонтальные прямые 3, 3’, 4, 4’ — изотропным оболочкам (то есть отвечают случаю to, = to2 = 0), изготовленным из материала связующего и имеющим те же характерные размеры. Линии 1, 1’, 3, 3’ определены для длинных (L = 3 м), остальные линии — для коротких цилиндрических оболочек (L = R = 0,5 м).

Показанные на рисунке 2 кривые характеризуют податливость рассматриваемых металлокомпозитных тонкостенных конструкций в условиях установившейся ползучести в зависимости от угла спирального армирования ψ. Вид кривых свидетельствует о существенной и немонотонной зависимости податливости от структуры армирования, а анализ их поведения позволяет выбрать такие структуры армирования (из рассматриваемого класса), которые при заданном нагружении обеспечивают наибольшую или наименьшую податливость соответствующей конструкции в условиях установившейся ползучести; в частности, при рассматриваемых характерных размерах конструкций и уровне их нагружения наименьшие скорости прогиба развиваются в оболочках, армированных в окружном направлении (у = п / 2), и имеют порядок 6 -10-2 мкм/ч (см. правые участки кривых 1, 1’, 2, 2’ при у« 1,5). С точки зрения минимизации податливости в условиях установившейся ползучести такие структуры армирования можно считать рациональными. Многочисленные расчеты, проведенные автором, показали, что при других условиях нагружения или других характерных размерах оболочек наименьшие по модулю скорости прогиба развиваются в конструкциях, армированных по другим направлениям. Так для весьма коротких цилиндрических оболочек (L ^ R), которые можно рассматривать как пологие, рациональной в указанном смысле является продольная (у = 0) структура армирования, о чем в определенной степени свидетельствует поведение кривой 2’ (Рис. 2, а) в окрестности точки у = 0. При учете же влияния днища (F10 = Rqz /2 ^ 0, см. (11)) рациональными могут быть и спиральные структуры армирования (0 < у < п / 2 ), отличные от меридиональных (у = 0) и окружных (у = п / 2 ) структур. Следовательно, при разных видах и уровнях нагружения и при разных габаритах конструкций рациональными с точки зрения минимизации величин w, будут разные структуры армирования, которые в общем случае могут и не совпадать с рациональными структурами, определенными на основе критериев кратковременной прочности [8].

Правые участки (при у> 1) кривых 1 , 1’ , 2 , 2’ на рисунке 2 лежат ниже горизонтальных прямых 3 , 3’ , 4 , 4’ , что означает: замена изотропных металлических оболочек из сплава АМг3 или меди на соответствующие армированные металлокомпозитные изделия при у >  1 приводит к резкому (в разы и на порядки) уменьшению их податливости в условиях установившейся ползучести. Кривая 2’ (Рис. 2, а ) всюду лежит ниже прямой 4’ , поэтому в случае короткой оболочки с жестко защемленными кромками, выполненной из сплава АМг3, замена ее на металлокомпозитную АМг3–У8А-оболочку при любых структурах армирования (из рассматриваемого класса) приводит к уменьшению податливости конструкции в условиях установившейся ползучести.

Линии 1’–4’ всюду лежат ниже линий 1 – 4 соответственно, что означает: замена шарнирного опирания кромок цилиндрической оболочки на жесткое защемление позволяет уменьшить податливость таких конструкций при установившейся ползучести. Однако, как видно из поведения линий 1 , 1’ , 3 , 3’ и 4 , 4’ , для длинных металлокомпозитных оболочек (кривые 1 , 1’ ) и для изотропных металлических оболочек (прямые 3 , 3’ и 4 , 4’ ) замена типа опирания кромок приводит к незначительному

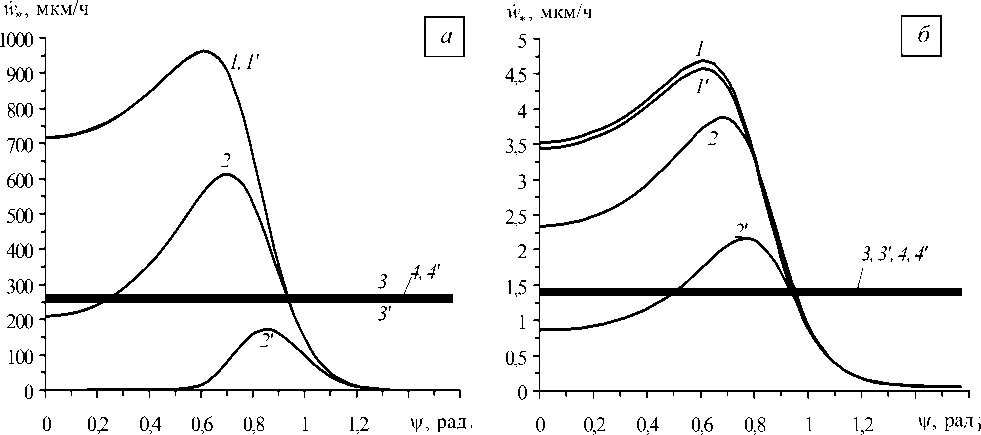
Рис. 2. Зависимости максимальных скоростей прогибов цилиндрических оболочек от угла спирального армирования для различных композиций: АМг3–У8А-композиция ( а ), Cu–У8А-композиция ( б )

уменьшению податливости в условиях ползучести. В случае же коротких цилиндрических оболочек и пологих оболочек другой геометрии замена шарнирного опирания кромок на жесткую их заделку приводит к существенному уменьшению податливости таких тонкостенных конструкций, работающих в условиях установившейся ползучести [2].

Кроме того, ординаты точек кривых на рисунке 2, б имеют значения на два порядка меньше, чем ординаты точек соответствующих кривых на рисунке 2, а . Следовательно, скорость прогиба при установившейся ползучести в конструкциях из АМг3–У8А-композиции много больше, чем в соответствующих изделиях из Cu–У8А-композиции, что вполне согласуется с поведением кривых установившейся ползучести 1 , 3 , приведенных на рисунке 1. Это означает, что замена связующего из сплава АМг3 на связующее из твердой меди также позволяет существенно уменьшить податливость металлокомпозитных оболочек в условиях установившейся ползучести. Здесь уместно подчеркнуть, что при рациональных структурах армирования ( ^ = п / 2 ) максимальные скорости прогибов в условиях ползучести в рассматриваемых конструкциях, выполненных из обеих металлокомпозиций, примерно одинаковы и лежат в диапазоне 0, 057...0, 059 мкм/ч , то есть различаются менее чем на 5 %.

Изменение структуры армирования приводит не только к количественному, но и к качественному изменению поведения функции скорости прогиба w ( x 1 ) в исследуемых оболочках. Так на рисунке 3 изображены зависимости w от безразмерной продольной координаты x = x 1 [L для трех структур армирования цилиндрических оболочек из Cu–У8А-композиции при шарнирном опирании кромок. Рисунок 3, а содержит результаты расчетов для длинных ( L = 3 м), а рисунок 3, б — для коротких ( L = 0,5 м) оболочек. Кривые 1 получены при у = 0, кривые 2 — при у = п / 5, кривые 3 — при у = 7 п /20. Вид кривых свидетельствует, что при структурах армирования, близких к рациональным (см. график 3 ), в рассматриваемых оболочках доминирует основное безмоментное напряженное состояние (центральные участки кривых 3 горизонтальны); с увеличением угла армирования ( и >  п/2) зоны краевых эффектов существенно уменьшаются. Эпюры скоростей прогибов при установившейся ползучести w ( x ) в оболочках с рациональными структурами армирования ( у = п/2) качественно подобны кривой 3 (Рис. 3, а ), но зоны краевых эффектов в них еще меньше.

Выше исследовалась установившаяся ползучесть цилиндрических оболочек постоянной толщины 2 H , = 2 см. Варьируя же длину оболочки (сравним кривые

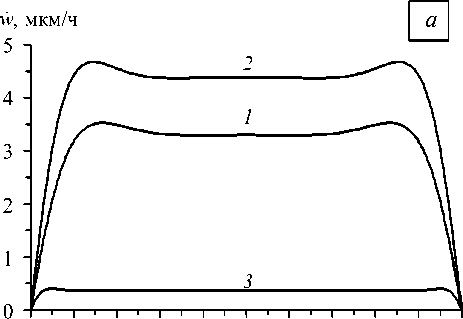
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 x

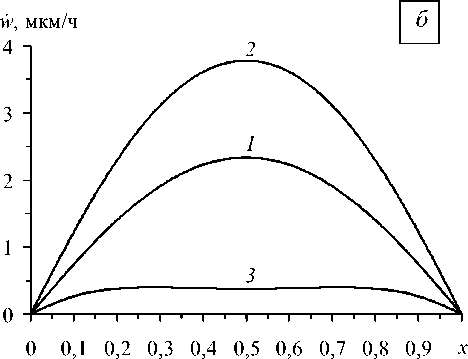
Рис. 3. Зависимости скоростей прогибов установившейся ползучести от безразмерной продольной координаты при трех структурах армирования длинных ( а ) и коротких ( б ) цилиндрических оболочек

с одинаковыми номерами на рисунке 3) и распределение толщины 2 H ( х 1 ) в осевом направлении, можно управлять податливостью конструкции в условиях ползучести. Об этом свидетельствует и рисунок 4, на котором изображены кривые, характеризующие зависимость максимального значения скорости прогиба в условиях ползучести w , ( 5 ) = max |iW ( x 1 ; 5 )| шарнирно опертых оболочек разной длины от значения параметра толщины 5 (см. (18)) при прежнем характерном значении толщины 2 H , = 2 см. Кривые 1 , 1’ рассчитаны для коротких оболочек ( L = 0,5 м), кривые 2 , 2’ — для длинных оболочек ( L = 3 м). Рисунок 4, а отвечает изотропным оболочкам из твердой меди, а рисунок 4, б — металлокомпозитным конструкциям при окружном армировании ( у = п /2), причем кривые 1 , 2 рисунка 4, б соответствуют оболочкам из Си-У8А-композиции, а линии 1’ , 2’ — из АМг3–У8А-композиции. Заметим, что ординаты точек кривых рисунка 4, б при 5 = 1 равны ординатам точек соответствующих кривых 1 , 2 рисунка 2 при ^ = п / 2 .

Все кривые рисунка 4 имеют локальные минимумы, которым соответствуют рациональные распределения (18) толщин оболочек, обеспечивающие наименьшие скорости прогиба в условиях ползучести. Из сравнения ординат точек на этих кривых при 5 = 1 (оболочки постоянной толщины) с ординатами точек локальных минимумов можно заключить, что в некоторых случаях за счет рационального распределения толщины можно на несколько десятков процентов уменьшить скорости прогибов точек оболочки, повышая тем самым сопротивляемость конструкции в условиях ползучести. Так на кривой 1 (Рис. 4, а ) локальный минимум реализуется при 5 « 0,5 ; максимальная скорость прогиба w , ( 5 ) при этом на 13,9 % меньше, чем в соответствующей короткой оболочке постоянной толщины (см. кривую 1 (Рис. 4, а ) при 5 = 1).

Локальные минимумы всех кривых рисунка 4 б и кривой 2 рисунка 4, а наблюдаются в точках 5 = 1,05 » 1, поэтому длинные оболочки (как изотропные, так и композитные), а также короткие металлокомпозитные оболочки (рассматриваемых размеров) постоянной толщины при заданном уровне нагружения могут рассматриваться как рациональные или близкие к ним в указанном выше смысле. Это объясняется тем, что в длинных оболочках постоянной толщины почти всюду имеет место напряженное состояние, близкое к безмоментному и однородному, на которое локализованные у кромок краевые эффекты влияют незначительно (это влияние сказывается на кривых 2 и 2’ в том, что их минимум реализуется при 5 = 1,05, а не строго при 5 = 1). Что касается

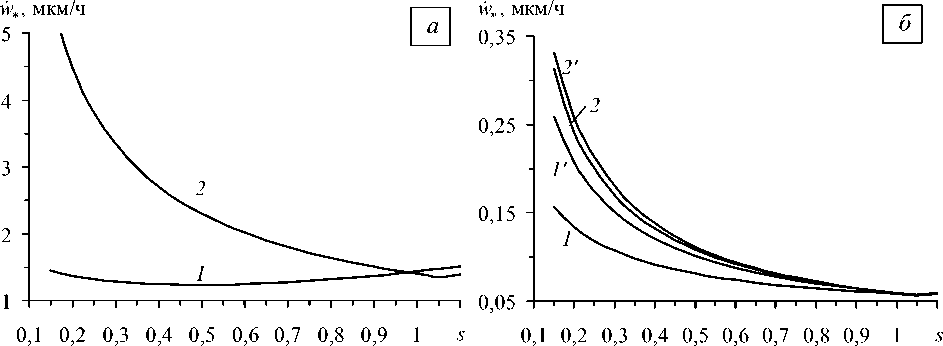
Рис. 4. Зависимости максимальных скоростей прогибов цилиндрических оболочек в условиях установившейся ползучести от параметра распределения толщины для изотропных (а) и металлокомпозитных (б) конструкций коротких металлокомпозитных оболочек заданных размеров, армированных в окружном направлении (у = п /2), то, как уже отмечалось выше, для них характерны такие же особенности деформирования в условиях ползучести (о чем качественно свидетельствует, например, поведение кривой 3 на рисунке 3, б), поэтому-то кривые 1, 1’ на рисунке 4, б также имеют локальные минимумы при s = 1,05 .

З а м е ч а н и е 2. Вернемся к рисунку 2. Некоторые участки кривых 1 , 1’ , 2 , 2’ лежат выше прямых 3 , 3’ , 4 , 4’ , то есть при определенных структурах армирования металлокомпозитные оболочки могут обладать большей податливостью в условиях ползучести, чем аналогичные изотропные оболочки, изготовленные из материала связующего. Это обстоятельство является следствием того, что согласно [1] в расчетах используется предложенная Ю.В. Немировским структурная модель армированного слоя с одномерным напряженным состоянием в волокнах, в рамках которой поперечные напряжения в арматуре (как нормальные, так и касательные) не учитываются. Таким образом, в модели отображается неидеальность механического контакта между арматурой и связующим (разрушенный контактный слой), что нередко наблюдается на практике при перекрестном армировании [17]. Поэтому при определенных структурах армирующие волокна как бы не участвуют в работе композита при его деформировании, что в условиях ползучести и приводит при этих структурах армирования к большей податливости металлокомпозитных оболочек по сравнению с аналогичными изотропными конструкциями, выполненными из материала связующей матрицы. Следовательно, все результаты, полученные в настоящем исследовании, можно трактовать как соответствующие одному из неблагоприятных, но встречающихся на практике случаев, а именно неидеальному механическому контакту компонент композиции. Более сложные модели неупругого деформирования перекрестно армированных металлокомпозитов, учитывающих полный контакт волокон со связующим, автору не известны.

6.    Заключение

Проведенный анализ деформирования металлокомпозитных оболочек, работающих в условиях установившейся ползучести, показывает, что армирование тонкостенной конструкции при определенных структурах армирования (даже в случаях неидеального контакта компонент композиции) позволяет существенно, иногда на порядки, уменьшить по модулю скорости перемещений точек срединной поверхности по сравнению со скоростями перемещений в изотропных конструкциях той же геометрии, выполненных из материала связующей матрицы.

Если для пологих оболочек, нагруженных в поперечном направлении, замена шарнирного опирания кромок на жесткую их заделку приводит к существенному уменьшению податливости конструкции в условиях ползучести, то для оболочек большой кривизны эффект от этого незначителен. Рациональное профилирование пологих оболочек также существенно уменьшает их податливость в условиях ползучести, в то время как профилирование оболочек большой кривизны (например цилиндрических), в силу доминирования в них безмоментного напряженного состояния, может оказаться малоэффективным.

Варьирование структуры армирования приводит к значительному изменению податливости оболочек в условиях ползучести, поэтому при проектировании металлокомпозитных изделий целесообразно осуществлять оптимизацию структур армирования по критериям податливости конструкции в условиях ползучести или критериям длительной прочности. При разных видах и уровнях нагружения тонкостенных конструкций и их размерах рациональными (оптимальными), например с точки зрения минимизации по модулю скоростей установившейся ползучести, являются разные структуры армирования. Так для весьма коротких цилиндрических оболочек (которые являются пологими), нагруженных внутренним давлением, рациональной будет продольная структура армирования, а для цилиндрических оболочек большой или средней длины — окружная. Эффективные с позиций кратковременной прочности проекты армирования (определению кратковременной прочности посвящена многочисленная литература по механике композитов) могут оказаться неэффективными для конструкции, работающей в условиях установившейся ползучести. Поэтому имеет смысл осуществлять многоцелевую оптимизацию конструкций, работающих в условиях длительного нагружения, как по критериям кратковременной прочности, так и по критериям длительной прочности или условиям нормальной их эксплуатации при ползучести.

Работа выполнена при финансовой поддержке РФФИ (проект 10-01-90402-Укр_а) и Президиума СО РАН (Постановление № 10 от 15.01.09, проект 72).