Расчет напряженно-деформированного состояния среднего уха при его тотальной реконструкции с учетом влияния остатков тимпанальной мембраны

В оториноларингологии существует несколько видов хирургических операций по реконструкции среднего уха. Механические аспекты подобных операций и их классификация в зависимости от дефектов и степени патологии приведены в статье [11]. Наиболее трудным как с точки зрения техники операционного вмешательства, так и с точки зрения достижения ощутимых результатов по восстановлению или улучшению слуха является случай тотальной реконструкции. Часто данный вид операций предполагает реконструкцию тимпанальной мембраны (ТМ), а также замену цепи косточек «молоточек–наковальня» на имплантат - искусственный Т-образный протез [11] (рис. 1). Данный протез своим основанием склеивается с мембраной, а другим концом анкируется на головку стременной косточки в случае ее подвижности.

С целью фиксации протеза и достижения его устойчивости в послеоперационный период длина протеза l выбирается несколько больше расстояния от барабанной перепонки до головки стремени в нормальном состоянии. Наличие указанного положительного приращения длины протеза неизбежно влечет за собой

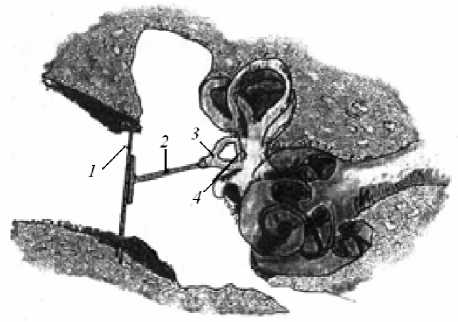
Рис. 1. Реконструированное среднее ухо: 1 – тимпанальная мембрана, 2 – T-образный протез, 3 – стремя, 4 – основание стремени появление начальных напряжений и деформаций в восстановленной ТМ, в связке овального окна, а также в сочленении «протез–стремя» [8]. Как следствие, данные напряжения приводят к смещению спектра собственных частот восстановленной колебательной системы среднего уха [4]. Степень искажения собственных частот может быть значительной и приводить к заметной потере порога восприимчивости звукового сигнала, присущего нормальному уху. Другими негативными последствиями выбора неоптимальной длины протеза и его неправильной пространственной ориентации может быть ограниченная подвижность основания стремени, а также «преждевременная» преднапряженность мышцы стременной косточки (которая в норме имеет место лишь при большой интенсивности воспринимаемого звукового сигнала).

Напряженно-деформированное состояние реконструированного среднего уха и его пространственная конфигурация сильно зависят от геометрических параметров протеза, от места его установки на барабанную перепонку и от способа реконструкции самой барабанной перепонки.

В случае тимпанопластики используются несколько видов Т-образных протезов, которые изготавливаются, как правило, из золота или титана. На рис. 2 изображены два типа протезов, выпускаемых фирмой KURZ Medical, Inc [10]. Протез типа « CliP^® Partial Prosthesis Dresden » отличается тем, что имеет очень гибкий стержень, который при анкировании на головку стремени может быть изогнут с учетом индивидуальной архитектуры среднего уха пациента; для протеза « Düsseldorf BELL Partial Prosthesis » характерно эксцентричное расположение стержня относительно основания протеза.

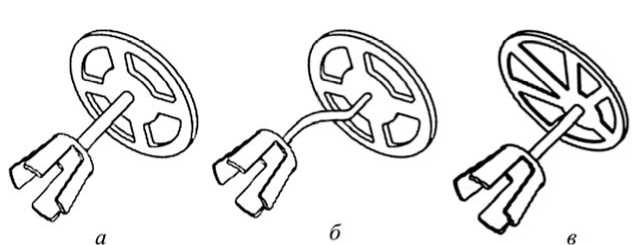
Рис. 2. Типы используемых протезов: а, б – CliP® Partial Prosthesis Dresden, в – Düsseldorf BELL Partial Prosthesis

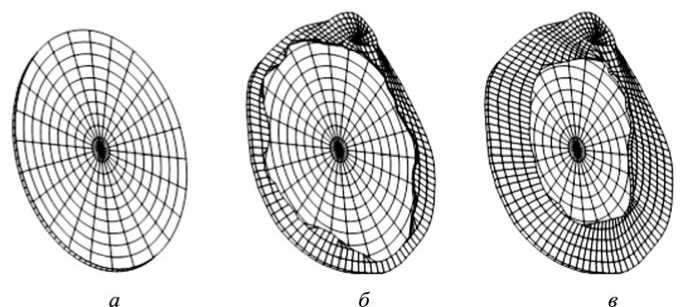
Рис. 3. Способы реконструкции барабанной перепонки с использованием хряща: а – техника « cartilage plate », б – техника « large island », в – техника « small island »

Данные протезы сильно различаются своими динамическими характеристиками (в частности, моментами инерции), а значит, выбор в пользу одного из них может сильно повлиять на успех операции. Следует отметить, что вопрос об оптимальном выборе протеза до сих пор остается неизученным. В нашем случае, при решении статической задачи о расчете начальных напряжений, выбор типа протеза является непринципиальным.

Перейдем к классификации техники реконструкции ТМ [15]. В зависимости от степени повреждения производят полную замену поврежденной мембраны имплантатом (рис. 3, а ), а также наложение имплантата на остатки барабанной перепонки (рис. 3, б , в ). Часто в качестве материала используется хрящевая ткань ( cavum conchae , tragus ).

Расчет начальных напряжений при тимпанопластике в случае полной реконструкции мембраны (см. рис. 3, а ) был выполнен в работах [5, 9, 14]. При этом в статье [14], применяя асимптотический метод, исследовали случай, когда центр основания протеза расположен вблизи центра восстановленной мембраны. Наоборот, в работе [9] методом конечных разностей изучен случай эксцентричного крепления протеза и мембраны. В работе [5] показано, что наряду с основным устойчивым положением равновесия восстановленной колебательной системы среднего уха существуют смежные устойчивые и неустойчивые равновесные положения, характеризующиеся более высоким уровнем потенциальной энергии.

В настоящей работе мы будем рассматривать технику « small island » (см. рис. 3, в ). В этом случае основание протеза практически полностью закрывает отверстие в поврежденной барабанной перепонке, что позволяет рассматривать восстановленную ТМ как двухслойную пластинку.

• 2.    М АТЕМАТИЧЕСКАЯ МОДЕЛЬ

Не умаляя общности, любой из изображенных на рис. 2 протезов будем рассматривать как твердое тело, состоящее из двух частей: круглой абсолютно твердой пластинки радиусом b и гибкого стержня, наклоненного к плоскости основания (круглой пластинке) под углом ψ. Общую длину протеза обозначим через l .

Рассматривая технику реконструкции мембраны типа « small island » (см. рис. 3, в ), восстановленную ТМ будем трактовать как двухслойную круглую пластинку. Слой живой ткани барабанной перепонки имеет сложную структуру и сам по себе состоит из четырех слоев. Наружный слой является продолжением кожи слухового прохода, а внутренний – продолжением слизистой оболочки среднего уха.

Ненатянутая часть барабанной перепонки, носящая название pars flaccida (или мембрана Шрапнелля), состоит только из этих двух слоев, в то время как натянутая часть pars tensa включает еще два дополнительных слоя: радиальные волокна под кожным слоем и нерадиальные волокна, расположенные между слоями радиальных волокон и слизистой оболочки. Учет анизотропии и неоднородности важен при исследовании динамики барабанной перепонки в норме [15]. В нашем (статическом) случае рассматривается упрощенная модель, согласно которой остаток тимпанальной мембраны трактуется как один однородный изотропный слой толщиной h ₁ . В качестве модуля упругости E ₁ и коэффициента Пуассона σ ₁ для данного слоя примем значения, совпадающие с соответствующими величинами для pars tensa барабанной перепонки в норме. Для хрящевого слоя (имплантата) аналогичные параметры - h ₂ , E ₂ , σ ₂ .

Считаем, что в результате склеивания реконструированной ТМ с основанием протеза по линии сопряжения (окружности) реализуются условия жесткой заделки для круглой пластинки. Таким образом, восстановленную ТМ можно моделировать как двухслойную кольцевую упругую пластинку с внешним и внутренним радиусами a и b соответственно.

Введем глобальную систему координат Oxyz , связанную с центром пластины (рис. 4). Здесь ось Oz направлена в сторону внешнего уха, а ось Oy – по линии “ malleus manubrium ”, то есть вдоль линии сопряжения молоточка с тимпанальной мембраной в норме. После фиксации протеза в полости среднего уха внутренний контур кольцевой пластины перемещается вдоль оси Oz на величину w_p и поворачивается вокруг некоторой оси O′O″ , проходящей через центр основания протеза C ( x_c , y_c , 0), на угол θ _p (рис. 5, а ). Введем также систему координат Cx′y′z′ , связанную с центром основания протеза, так чтобы ось Cy′ совпадала с осью поворота O′O″ . Обозначим угол между осями Oy и Cy′ через φ . Заметим, что ориентация оси поворота O′O″ протеза является неизвестной и подлежит определению.

Пусть S ξηζ - система координат, связанная с основанием стремени в ненапряженном состоянии (то есть до анкирования протеза на стремя). Здесь точка S совпадает с центром основания стремени, а ось S ζ направлена к головке стременной косточки. Заметим, что ориентация стремени в пространстве зависит от индивидуальной архитектуры пациента. Однако будем считать, что направляющие косинусы осей системы координат S ξηζ по отношению к глобальной системе координат Oxyz известны.

ось поворота основания протеза

Рис. 4. Восстановленная ТМ, протез и стремя в ненапряженном состоянии

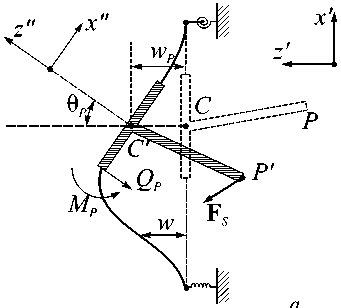
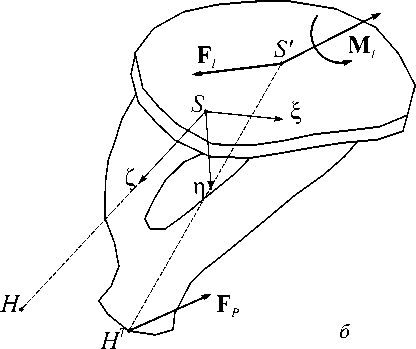
Рис. 5. Перемещения и повороты протеза ( а ) и стремени ( б )

Проводимость звукового сигнала через реконструированную трансформационную систему среднего уха зависит от условий сопряжения протеза и стременной косточки. Как указывает Ойбер [8], жесткое крепление протеза на головке стременной косточки гарантирует передачу звукового сигнала с минимальной потерей энергии. С другой стороны, фиксация протеза на головке стремени должна быть в некоторой степени мягкой, исключающей возможный вывих стремени ( stapedial luxation ). Данный вывих наблюдается при усилии в сочленении «протез–стремя», равном 350 × 10 ^{- 3} Н [12]. Даже если лепестки протеза (см. рис. 2) прижаты к головке стремени достаточно плотно, существует малая брешь между протезом и косточкой, которая впоследствии заполняется жидкостью или кровью. Следует также принять во внимание разность внешнего атмосферного давления и давления в полости среднего уха. Во время операции разность давлений равна нулю, однако в послеоперационный период оно возрастает и через 2–4 месяца достигает величины P_s = 20 Па . Возрастающая разность давлений и наличие малой бреши в сочленении «протез– стремя» приводят к малым поворотам протеза и стремени. Данные повороты позволяют допускать (с некоторой долей погрешности) реализацию условий шарнирного соединения в соединении «протез–стремя». Обозначим через F_s ( X_s , Y_s , Z_s ) силу, действующую со стороны стремени на протез в данном соединении. Соответственно, сила, действующая со стороны протеза на стремя, есть величина F_p = - F_s .

После введения протеза в область среднего уха основание стремени переместится в точку S′ с координатами ( ξ _{s ′} , η _{s ′} , ζ _{s ′} ) и повернется на углы α_ξ , α_η , α_ζ вокруг соответствующих осей (см. рис. 5, б ).

Двенадцать введенных параметров X_s , Y_s , Z_s , w_p , θ _p , φ , ξ _{s ′} , η _{s ′} , ζ _{s ′} , α_ξ , α_η , α_ζ характеризуют напряженно-деформированное состояние и пространственную конфигурацию реконструированного среднего уха. Для нахождения этих параметров необходимо выписать 12 уравнений равновесия реконструированной системы среднего уха.

• 3.    У РАВНЕНИЯ РАВНОВЕСИЯ ПЛАСТИНКИ

В полярной системе координат, связанной с Oxyz , введем прогиб пластинки w ( r , ϕ ). В качестве уравнения равновесия слоистой пластинки рассмотрим уравнение [2]

( 1 - c 1 A ) A 2 х ( r , ф ) = P ,

где A - оператор Лапласа в полярной системе координат, х(r, ф) - функция прогиба, связанная с самим прогибом w(r, ф) соотношением w ( r, ф)=(1 - С 2A)x( r, ф) .                                  (2)

О h ²         h ²

Здесь c 1 = в , c ₂ = ~р", h — общая толщина пластинки, P - разность атмосферного давления и давления в полости среднего уха, а параметры θ и β зависят от количества слоев пластинки. В нашем случае приняты значения θ = 0,02, β = 6, соответствующие двухслойной пластинке. Заметим, что в первые послеоперационные дни разность давлений мала, так что можно принять P = 0, однако с течением времени она возрастает, достигая через 2-3 месяца величины P = 20 Па .

Рассмотрим граничные условия для уравнений (1), (2). На внутреннем и внешнем контуре примем условие жесткой заделки [2]:

dw              dx 6 = wp+b cos ф tg0 p, —   = cos ф tg0 p, —   = 0, r b                         dr                     dr r=b                             r=b (3) ,         dx         dw w = 0, —  = 0, —  = 0, 1 r=Г         dr             ar r =Г              r=Г (4) где r = Г(ф) = aa2 —52 sin2 (ф + ф-фc)-5c cos(ф + ф-фc),               (5)

⁵ c = xR+y! , ^cos ф c = x /S c , sin ф c = y_c /5 c .

Считаем, что центр основания протеза (точка C ) находится на относительно малом расстоянии от центра восстановленной мембраны (точка O ), так что параметр ц = 5 c/a можно считать малым. Разложим функцию (5) в ряд по степеням малого параметра µ.

r = a

1 - ц cos ( ф + ф-ф _c ) - ц ²

Г 11            \)

4 - 4^cos2 ( ф+^ф-ф c ) J⁺ O ( ц )

Здесь и ниже символ O ( ц v ) означает величину, имеющую порядок ц v при ц ^ 0.

Следуя [14], решение уравнения (1) будем искать в виде асимптотического разложения по степеням µ, представив каждый член данного разложения в виде ряда Фурье

х ( r , ф ) = 5Ух , ( r , ф ) ,                                ⁽⁷⁾

i = 0

^

Х , -( r , ф ) = х 0 ( r ) ⁺ Е [х _;'к ( r ) ^cos k ( ф + ^ф-ф c ) ⁺ Х /k ( r ) sin ^k ( ф + ^ф-ф c ) ] .        ⁽⁸⁾

к = 1

Подставим (7) в уравнение (1) и граничные условия (3), (4) и приравняем коэффициенты при одинаковых степенях ц . В результате получим последовательность краевых задач относительно функций х i . При этом заметим, что в силу разложения (6) граничные условия относительно функции х i на внешней кромке (4) будут однородными при i = 0 и неоднородными при i >  1. Решая каждую из возникающих краевых задач в виде (8), приходим к соотношениям относительно неизвестных функций у ° , X ck , X 1k , фигурирующих в (8),

00020  02

Xi (r) = A + Bir + Ci Inr + Dir

In r + E ”I °

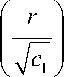
+ F-K°

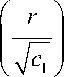
c , s                 c , s           c , s 3 c , s

X ii (r ) = An r + Bn r + Ci

- + D C s r In r + E Cs r

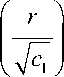
K 1

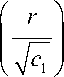
c,s / \      cc,s k ,  r>c,s k + 2

X ik ( ^r ) = A ik ’ ^{r +} B ik ’ ^r

+ Cc,s —+DC-s —+Ec-s I, ik k        ik k- 2       ik k rr

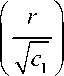
c , s

^{+ 1} ik

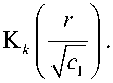
Здесь k = 2, 3, …; I_n ( x ), K_n ( x ) – модифицированные функции Бесселя первого и второго рода, а неизвестные коэффициенты находятся из граничных условий (3),(4) с учетом (6).

Найденный в соответствии с (2), (7)–(9) прогиб пластинки позволяет определить возникающие в срединной поверхности перерезывающие силы и изгибающие моменты.

д ( д ² w 1 д w   1 д ² w

'д2w одw  о д2w

д r д r ² r д r r ² дф ²

д r ² r д r r ² дф ² k                         /

Здесь D = Eh у [ 12 ( 1 -о ² ) ]

и h - усредненная цилиндрическая жесткость и общая толщина двухслойной пластинки соответственно, а E, о - приведенные модуль Юнга и коэффициент Пуассона, определяемые по формулам [2], о =

E ₁ h₁ o ₁ E ₂ h ₂ о ₂ 1 -о 2 1 - о 2

E ₁ h ₁     E ₂ h ₂

1 - о 2 1 - о 2

1 -о( Eh E₂h₂ С E = --^^у + ^^у

h k 1 - о1   1 - о 2 ^

Напомним, что стоящие в (11) величины с индексами 1 соответствуют живой ткани остатков тимпанической мембраны, а параметры с индексами 2 - используемому для реконструкции мембраны хрящу.

Интегрируя перерезывающие силы и изгибающие моменты (10) по внутреннему контуру r = b, получим результирующие силы и моменты, действующие со стороны реконструированной мембраны на основание протеза (см. рис 5, а ):

Qp = -2пbD [K1 wp + цк2 cos (ф - фc) sin 0p + O (ц2)],

Mp =-пbD[к3 sin 0pwp +цк4 cos(ф-фc) wp + O(ц2)] ,

M Q =-n bD [к ₅ w_p + цк ₆ cos ( ф-ф c ) sin 0 _p + O ( ц ² ) ] .

Здесь M_Q - главный вектор моментов перерезывающих сил Q относительно оси поворота Cy ' (см. рис. 4) основания протеза, а соотношения для коэффициентов к i в силу их громоздкости здесь не выписаны.

• 4.    У РАВНЕНИЯ РАВНОВЕСИЯ ПРОТЕЗА

Поскольку протез совершает перемещение и поворот в плоскости, перпендикулярной оси Cy ', условия его равновесия могут быть записаны в виде трех скалярных уравнений. В силу того, что тангенциальные перемещения реконструированной пластинки в нашей (линейной) постановке во внимание не принимаются, мембранные усилия, действующие со стороны пластинки на основание протеза, могут быть проигнорированы. Таким образом, уравнение равновесия протеза в направлении оси x в данном приближении может быть опущено. Оставшиеся два уравнения имеют вид

(Xs cos ф + 7s sin ф) sin 0p - Z, cos 0p - Qp = 0, cos w cos (ф - фp) sin 0p - sin w cos 0p) -

■ Z _c (cos w cos ( ф-ф„ ) cos0„ + sin w sin0_n | + M_n + M_n = 0. s t         I          ^p 1 X p ^{p          p}             I            ^p 1            ^p          Q

-

К уравнениям (13) необходимо добавить условие того, что сила F_s лежит в плоскости поворота протеза

Y_s cos ф- X_s sin ф = 0.                              (14)

• 5.    У РАВНЕНИЕ РАВНОВЕСИЯ СТРЕМЕНИ

Геометрическое положение стремени в ненапряженном состоянии (до введения протеза) задается двумя точками H ( S _H , n _H , Z _H ) и S ( S S , П S , Z S ) (см. рис. 5). Тогда длина стремени

I, = V( S H -S SУ' + ( n H -n S ) ² + ( Z H -Z S ) ².                     (15)

После введения протеза длина стремени не изменится. Это можно записать соотношением l, V(SH^SJ + (nH^TSJ + (ZH^SJ ,                  (16)

где H'(SH‘, nH', ZH’) — новое положение головки стремени, которое будет совпадать с координатами конца стержня протеза.

Углы поворота стремени вокруг координатных осей находятся из формул ^(Z H -^Z S ⁾⁽ⁿ H ' -ⁿ S ^{, )-(n} H -ⁿ S ^)(Z H ' -^Z S ’)

sin a _S =----------------------2--------------2----------- ,

( Z H -Z S ) ⁺ ( n H -n S )

( S H -s S ) ( Z H -Z S ) - ( Z H -Z S ) ( S H -S S ) ( S H -S S ) ² + ( Z H -Z S ) ²

Заметим, что угол поворота а ^ стремени вокруг собственной оси Z здесь не выписан; он может быть найден из уравнений равновесия стремени (см. ниже).

Békésy [7] удалось экспериментально показать, что общая жесткость внутреннего уха зависит как от жесткости связки овального окна, так и от жесткости мембраны круглого окна, которое расположено на дне scala tympani . При этом у некоторых людей почти вся упругость приходится на кольцевидную связку стремени, в то время как у других сила упругого противодействия возникает только в мембране круглого окна [1]. В нашей работе рассматривается первый случай, когда силы упругости связок овального окна являются определяющими.

В работе [6] экспериментально получена матрица, описывающая упругие свойства связок овального окна,

" 51,4 -0,24 -1,37 0,04 9,66 0,35" -0,24 49,2 -0,6 -7,87 -1,01 -8,4 -1,37 -0,6 27,8 0,37 17,1 0,96 C =c RB   cref 0,04 -7,87 0,37 8,29 0,58 2,6 ,               (18) 9,66 -1,01 17,1 0,58 29,7 1,6 _ 0,35 -8,4 0,96 2,6 1,6 12,9 _ где коэффициент cref у разных людей может варьироваться от 0,035 Нмм 1 до 0,05 Нмм-1. Здесь принято среднее значение cref = 0,0425 Нмм-1. Произведение матрицы (6) на вектор перемещений и поворотов стремени определяет вектор соответствующих сил и моментов, возникающих со стороны связки овального окна,

( f'i5, fl,, f z, ml5, ml,, mlz ) = CRB (5S'.ns,zS',“s.a.“() .(19)

где F l ( J l 5 , f , , , f , z ) , M , ( m l 5 , m l _n , m l z ) — силы и моменты, действующие со стороны связок овального окна (см. рис. 5).

Тогда уравнения равновесия стремени запишутся в следующем виде:

Jl 5- fP 5= 0, Jln- fp n= 0, Jlz- fpz= 0,(20)

ml5+ПH-fpz-zH-fpn= 0, mln + zH-fp5-5H-fpz = 0, m.z = 0,(21)

где f_p 5 , f_{p n} , f_p z - проекции силы F _p , действующей со стороны протеза на стремя, на оси 5 , П , z соответственно (см. рис. 5, б ).

Из последнего уравнения в (21) находится угол поворота стремени a z вокруг собственной оси после ввода протеза. Наши последующие расчеты показывают, что данный угол является очень маленьким и может быть принят во внимание лишь при очень больших перемещениях стремени, близких к его вывиху. Данный результат хорошо согласуется с данными [3], согласно которым стременная косточка начинает закручиваться вокруг своей оси лишь при большой интенсивности падающей звуковой волны.

• 6.    Р ЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Выведенные двенадцать уравнений (13), (14), (16)–(21) позволяют найти параметры Xs, Ys, Zs, wp, 0p, ф, 5s., ns■, zs', a5, an, az, характеризующие напряженно-деформированное состояние реконструированного среднего уха и его пространственную конфигурацию после ввода протеза.

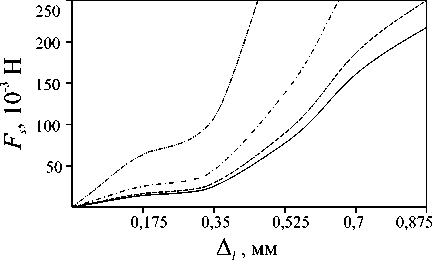
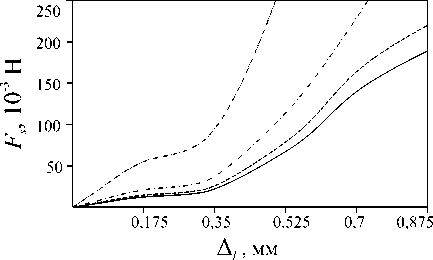
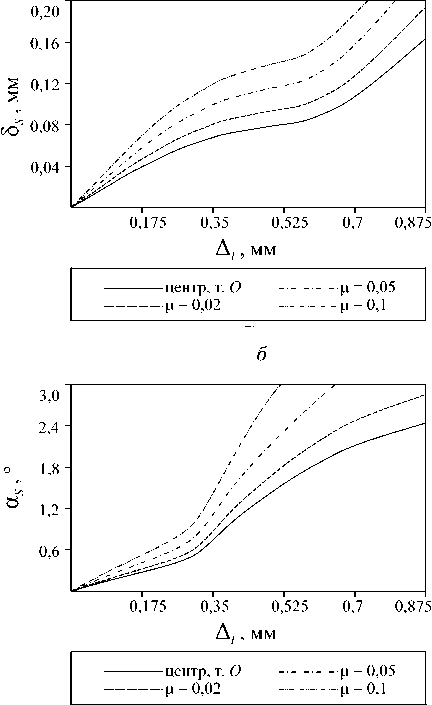
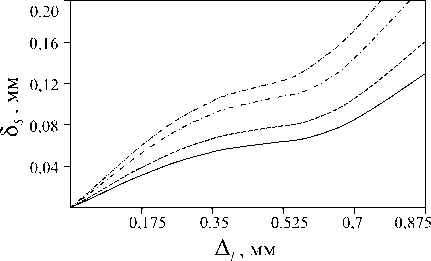
На рис. 6 изображены точки центра основания протеза на восстановленной ТМ (точки 1-6); при этом точки 1-3 лежат на линии OC_m , совпадающей по направлению с “ malleus manubrium ”, а точки 4-6 - на линии OC_p . Здесь O - центр восстановленной ТМ, C_m - средняя точка на “ malleus manubrium ”, а C_p - проекции головки стремени в ненапряженном состоянии на мембрану (точка “ posterior point ”). Были рассмотрены следующие значения параметра µ , характеризующего эксцентриситет соединения основания протеза и ТМ: µ= 0,02 для точек 1 и 4; µ = 0,05 для точек 2 и 5; µ= 0,1 для точек 3 и 6. Расчеты выполнялись при P = 0 Pa, a = 5 мм, b = 1,5 мм, h ₁ = h ₂ = 0,3 мм, E ₁ = 3 Н/мм² , σ ₁ =σ ₂ = 0,4 , E ₂ = 3,4 Н/мм² . В качестве координат головки стремени (точка H ) и центра ее основания (точка S ) (cм. рис 5, б ) до установки протеза в глобальной системе координат Oxyz были рассмотрены следующие значения: x = 2,29 мм, y = - 1, 65 мм, z = - 3, 32 мм; x = 3,64 мм, y = - 1,5 мм, z =- 6,5 мм. H  H  H  SSS

Приведенные параметры соответствуют архитектуре среднего уха среднестатистического взрослого человека.

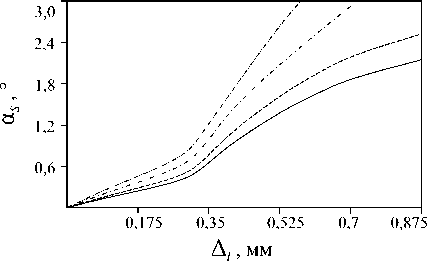
На рис. 7 представлены график и зависимос ти модуля силы F _S в соединении «протез–стремя», перемещения δ _s = V ξ ² _{S ′} + η ² _{S ′} + ζ ² _{S ′} основания стремени и угла его поворота α _S = arccos(cos α_ξ cos α_η ) как функции приращения длины протеза ∆ l = l - l _min для различных точек установки основания протеза на восстановленной ТМ. Здесь l _min -расстояние от головки стремени в свободном ненапряженном состоянии до точки крепления основания протеза на ТМ. Кривые на рис. 7, а , б , в соответствуют случаю, когда центр основания протеза лежит на линии “ malleus manubrium ” (в точках 1, 2, 3), а линии на рис 7, г , д , е - случаю, когда центр основания протеза находится между центром ТМ и точкой “ posterior point ” ( в точках 4, 5, 6). Расчеты выполнялись для значений приращения длины протеза в интервале 0 ≤ ∆ l ≤ 0, 875 . При этом, если усилие F_S достигало значения 250 × 10 ^{- 3} Н, то расчеты прекращались (напомним, что при F_S ≥ 350 × 10 ^{- 3} H имеет место вывих стремени).

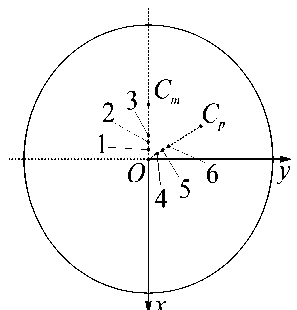
Рис. 6. Точки установки протеза на восстановленной ТМ в направлении

“malleus manubrium”

центр, т. О ----------р = 0,05 р = 0,02        -----------------р О, 1

в направлении к точке “posterior point”

центр, т. О ----------р = 0,05 р = 0,02        -----------------р 0,1

в

Рис. 7. Модуль силы F_s , перемещение основания стремени δ _S и угол поворота стремени α _s как функции параметра Δ l для различных положений основания протеза на восстановленной ТМ

г

центр, т. О ----------р = 0,05 р = 0,02        -----------------р —0,1

д

центр, т. О ----------р = 0,05 р = 0,02        -----------------р = 0,1

е

Как и следовало ожидать, с увеличением параметра ∆ l (при фиксированных точке крепления стремени с мембраной и угле ψ наклона стержня протеза к его плоскости) все величины, характеризующие напряженно-деформированное состояние системы, возрастают. Видно, что в интервале 0 ≤ ∆ l <  0,175 зависимость F_S , δ _S α _S от параметра ∆ l носит линейный характер, однако дальнейшее увеличение длины протеза

(о чем свидетельствуют кривые для F_S на рис. 7, а – г ) делает всю систему существенно нелинейной. При этом сравнение кривых, соответствующих различным параметрам µ (при фиксированном ∆ l ), указывает на то, что свойство нелинейности наступает тем раньше, чем дальше крепится основание протеза от центра ТМ. Объясняется данный эффект увеличением жесткости всей системы среднего уха в случае попытки установки основания протеза в точки мембраны, удаленные от ее центра. Таким образом, в случае крепления протеза в точку C_p (“ posterior point ”) или в близкие к ней точки, когда длина протеза может быть минимальной, неправильный подбор длины протеза может привести к значительным начальным напряжениям, что является крайне нежелательным. Аналогичный вывод можно сделать и относительно точки C_m -средней точки на линии “ malleus manubrium ”. Другими словами, напряженно-деформированное состояние реконструированной системы среднего уха является наиболее чувствительным, если основание протеза устанавливается на мембране в местах, близких к точкам C_p и C_m . Наиболее предпочтительными с точки зрения минимизации начальных напряжений являются точки крепления протеза, близкие к точке O - центру ТМ. Данный вывод хорошо согласуется с результатами работы [13], в соответствии с которыми наилучшая трансформация энергии звукового сигнала во внутреннее ухо наблюдается в случае, когда протез крепится как можно ближе к центру ТМ.

Благодарности

Исследования выполнены по заданию «Механика 4.09» Государственной комплексной программы научных исследований ГКПНИ «Механика» в Республике Беларуси на 2006-2010 гг.