Расчет оптимального времени истечения жидкого снаряда из сопла импульсного эжектора

Струйные насосы (эжекторы) широко распространены в энергетической, металлургической, химической, нефтяной и газовой промышленности в виде вакуумных насосов, компрессоров, смесителей [1–7]. Это обусловлено простотой конструкции, отсутствием подвижных частей и возможностями размещения в труднодоступных местах [8–10]. Однако разработка и внедрение струйных насосов часто сопряжены с необходимостью оптимизации схем использования, проведения комплексных расчетов геометрических и режимных параметров насоса и системы для исходных данных каждого конкретного проекта. Кроме того, для эжекторов, работающих непрерывно и с большим потреблением активной жидкости, энергоэффективность является одним из ключевых требований при проектировании. Одно из направлений исследований, посвящённых повышению эффективности эжекторов, нацелено на изучение эффектов использования пульсации активного потока. Так, в работах [11, 12] в качестве сопла активной жидкости используется струйный триггер, обеспечивающий заданную частоту пульсации потока. Такая конфигурация соплового блока также позволяет добиться лучшего перемешивания активной и пассивной сред и лучшего диспергирования газовой фракции.

В статье [13] предлагается импульсный эжектор, показанный на рис. 1, пульсация активного потока в котором осуществляется при помощи прерывателя 1, установленного в сопловом блоке 2. Авторы установили, что при малых степенях сжатия импульсный эжектор имеет более высокий КПД, чем классический жидкостно-газовый эжектор. Режим работы импульсного эжектора является «снарядным», то есть в течение времени выдержки прерывателя открытым формируется жидкий снаряд, который отсекается прерывателем при закрытии. При этом рабочий процесс такого струйного насоса основан преимущественно на сжатии газа жидкими снарядами.

Эжектор с прерывистой струей (см. рис. 1) работает циклически. Клапан-прерыватель, открывая и закрывая канал сопла (активной жидкости), создает нестационарное движение воды и воздуха в рабочей камере. При этом изменение параметров потока может происходить не только в течение одного цикла, но и от цикла к циклу [14, 15].

Рабочий процесс эжектора с прерывистой струей может быть разделен на две части: 1 - истечение активной жидкости через сопло (фаза разгона снаряда), 2 - увлечение пассивного воздуха жидким снарядом, движущимся в рабочей камере (фаза торможения наряда). Первая фаза происходит при открытии канала подачи активной жидкости, вторая - при перекрытии этого канала прерывателем.

Продолжительность формирования жидких снарядов характеризуется коэффициентом прерывистости, который выражает отношение времени истечения через сопло 0_о ко времени цикла [13]:

т _р =7 . (1) _ц

Именно в первой фазе снаряду передается энергия, за счет которой происходит работа по сжатию откачиваемого газа. Следует ожидать, что сама работоспособность импульсного струйного насоса зависит также от абсолютного времени выдержки прерывателя в состоянии «открыто» ввиду того, что жидкий снаряд должен сохранять свою целостность на всем пути от соплового блока до конца камеры смешения. А определение минимально необходимой энергии, достаточной для осуществления данного рабочего процесса, то есть оптимального времени выдержки прерывателя открытым, позволяет улучшить энергоэффективность эжектора.

Исследований, направленных на определение оптимального времени выдержки прерывателя открытым, обнаружить не удалось.

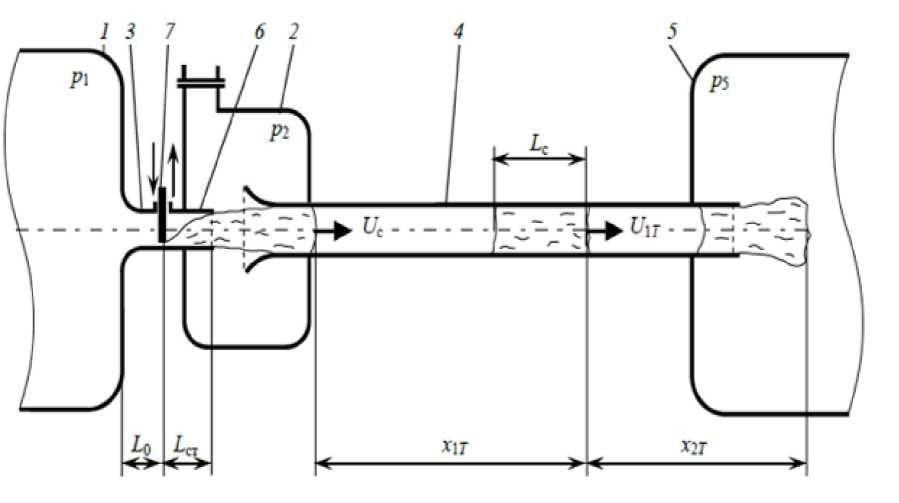
Рис. 1. Принципиальная схема струйного импульсного насоса

Fig. 1. Schematic diagram of a pulsed jet pump

Данная работа посвящена выявлению оптимального времени выдержки прерывателя активного потока струйного импульсного жидкостно-газового насоса в состоянии «открыто».

Для энергетического анализа жидкий снаряд рассматривается как несжимаемое тело, кинетическая энергия которого обеспечивает рабочий процесс импульсного эжектора. Кинетическая энергия жидкого снаряда пропорциональна квадрату его скорости, следовательно, для обеспечения наиболее эффективных режимов работы импульсного эжектора необходимо установить зависимость скорости снаряда от времени выдержки прерывателя в состоянии «открыто» [16].

Расчетная модель соплового блока

На рис. 2 показана расчетная схема соплового устройства импульсного эжектора с прерывателем [17]. При закрытом канале скорость истечения жидкости v ср равна нулю. Сразу после открытия канала скорость начинает расти от нуля до величины, соответствующей стационарному режиму истечения жидкости, зависящему от перепада давления на сопле p 1 – p 2 . В общем случае сопло может представлять собой цилиндрический насадок [18].

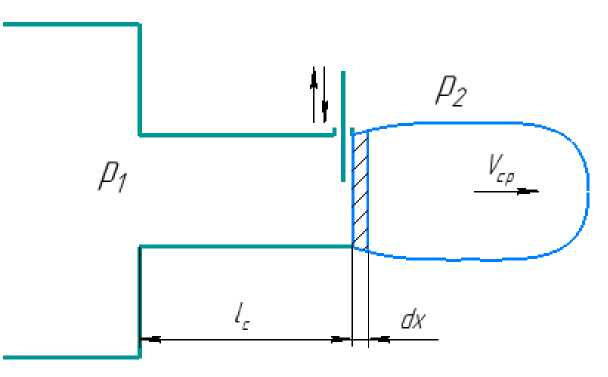
Рис. 2. Расчетная схема соплового устройства

Fig. 2. Design scheme of the nozzle device

Расчет величины скорости истечения жидкости через сопло, соответствующей стационарному режиму истечения, производится по уравнению Торричелли [19]:

2 ∙∆ P12

(l+fс)∙pж где ΔP12 – перепад давления на сопле; fс – коэффициент сопротивления сопла; Pж – плотность рабочей жидкости.

До достижения стационарной скорости истечения жидкости скорость истечения изменяется от 0 до Ko . Закономерность изменения скорости на срезе сопла может быть установлена с помощью уравнения энергии, включающего следующие допущения: жидкость несжимаема, открытие канала происходит мгновенно [20]:

Δ P12 =(1+f с )∙- ж∙ - ₊ P ж ^∙ k ^∙S ,                                                    (3)

где V – скорость в выходном сечении сопла; l_c – длина разгона (инерционная длина сопла).

Таким образом, энергия перепада давления Δ p 12 = p 1 – p 2 затрачивается сначала на разгон жидкости, а потом на стационарное истечение.

Проинтегрировав уравнение (3), получаем аналитическую зависимость скорости от времени:

V =   ∙ t ℎ    ^Δ ^ ∙( ^ с ) _∙^ =   ∙tℎ (- ∙( Г с ) _∙ t) ․                                      (4)

∙ p ж                                        ∙

Полученная аналитическая зависимость мгновенной скорости потока при нестационарном течении от времени открытия задвижки позволяет рассчитать оптимальное время истечения жидкости через сопло.

Результаты и обсуждения

На рис. 3, 4 проиллюстрирован ы графические зависимости скорости истечения жидкости через сопло от времени выдержки прерывателя в состоянии «открыто» при значении коэффициента сопротивления сопла f_c = 0,05, перепадах давления 100; 200; 300 и 400 кПа и инерционных длинах 0,1; 0,3; 0,5 и 1 м.

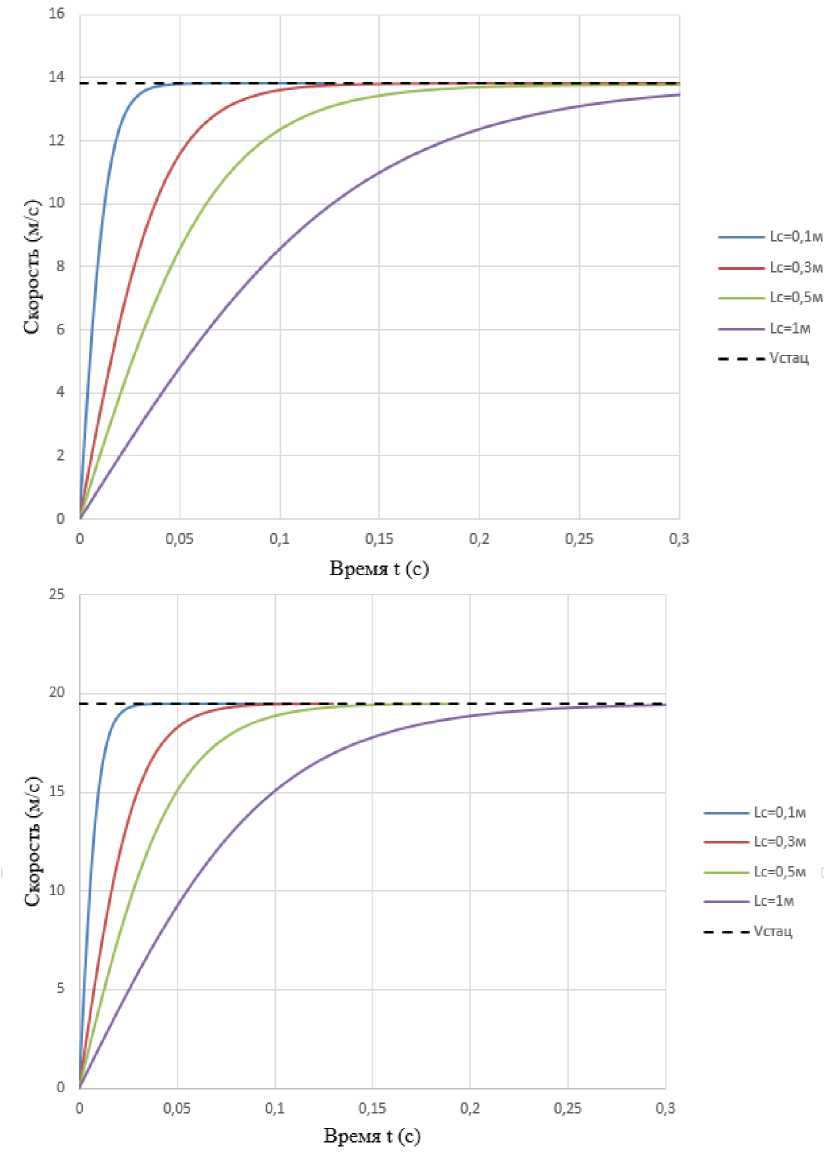
Рис. 3. График зависимости скорости от времени истечения жидкости через сопло задвижки при 100 и 200 кПа

Fig. 3. Graph of the dependence of the velocity on the time of the liquid flow through the valve nozzle at 100 and 200 kPa

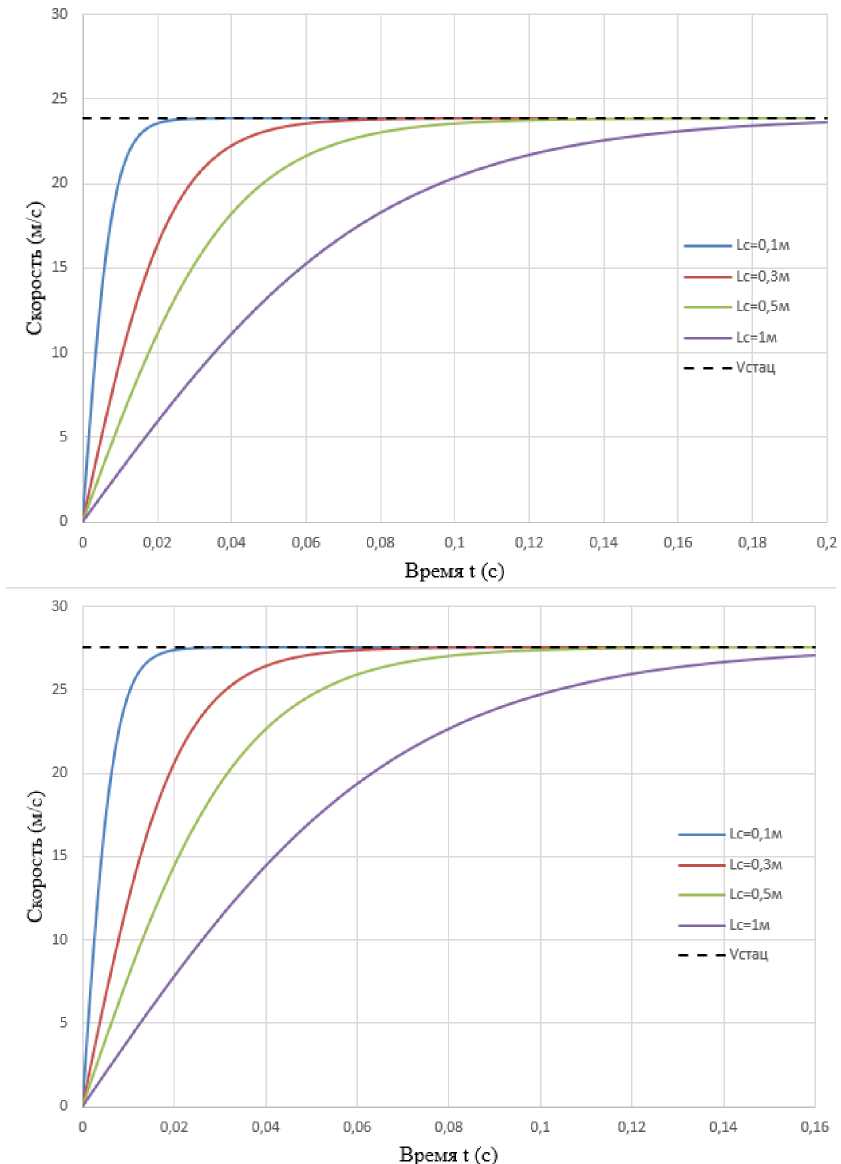
Рис. 4. График зависимости скорости от времени истечения жидкости через сопло задвижки при 300 и 400 кПа

Fig. 4. Graph of the dependence of the velocity on the time of the liquid flow through the valve nozzle at 300 and 400 kPa

Как видно из представленных графических зависимостей, при увеличении инерционной длины при одном и том же давлении время достижения стационарной скорости истечения жидкости снижается. Ранее [13] при исследовании импульсных эжекторов рассматривалось относительное время или коэффициент прерывистости, но не само время истечения жидкости через сопло. Од- нако, как показывает данное исследование, определение времени истечения жидкости через сопло позволяет более детально анализировать рабочий процесс импульсного эжектора: например, если для инерционной длины lc =1 м время открытия задвижки принять 0,1 секунды, то мгновенная скорость жидкого снаряда составит 8,55 м/с вместо возможных 13,8 м/с при времени открытия 0,3 секунды (см. рис. 3 левая часть). Анализируя полученные графики, можно определить оптимальное значение времени открытия, при котором достигается максимальная стационарная скорость движения снаряда для разных исходных данных соплового устройства. При этом следует отметить, что максимально достижимая скорость истечения жидкости из сопла определяет начальную скорость движения снаряда в камере смешения, а следовательно, и длину камеры смешения или, в случае решения обратной задачи, давление питания активной жидкости p1.

Исходя из полученных результатов, можно сформулировать методику расчета выдержки прерывателя в состоянии «открыто».

Исходных данные для расчета: перепад давления на сопле – Δ P12 ; коэффициент сопротивления сопла – f_с; плотность активной жидкости P _ж и инерционная длина сопла – l_c . В качестве примера примем следующие исходные данные: Δ p = 250кПа; f с = 0,05; p ж = 1000 кг ; l_c = 0,5 м. Алгоритм расчета следующий:

• 1)    определяется стационарная скорость истечения по формуле (2):

2∙250∙103 Па

= 21,82м; с

И» =

(1 + 0,05) ∙ 1000 кг

• 2)    вычисляется время открытия, выраженное из уравнения (4) в явном виде:

  t о

  
  

  2 ^∙ - ^∙ ^&.

  Vn ∙(1+fс) ^;

  
  
  
  

• 3)    рассчитывается необходимое время открытия для относительных скоростей движения жидких снарядов в некотором диапазоне с заданным шагом. Например, от 0,1 с до 1 с, с шагом 0,1. Результаты расчёта сведены в таблицу и проиллюстрированы на рис. 5.

  

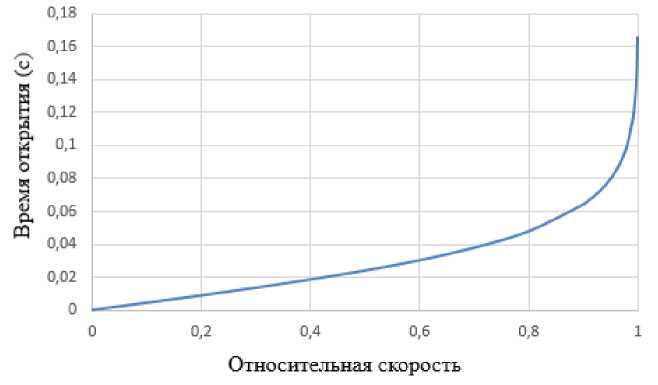
  Рис. 5. Зависимость времени истечения жидкости через сопло от относительной скорости

  Fig. 5. Dependence of the time of liquid flow through the nozzle on the relative velocity

  
  

Результаты расчета оптимального времени истечения жидкости через сопло The results of calculating the optimal flow time of liquid through the nozzle

V кГ	t о ,с	V ^	t о ,с	V кГ	t о ,с	V кГ	t о ,с	V ^	t о ,с
0,1	0,00438	0,3	0,0135	0,5	0,024	0,7	0,0379	0,9	0,0643
0,2	0,00885	0,4	0,0185	0,6	0,0303	0,8	0,048	0,999	0,1659

В зависимости от того, какое значение скорости необходимо, выбирается оптимальное время истечения жидкости через сопло. Рис. 5 показывает, что после момента времени 0,9 с изменение скорости практически не происходит. При этом дальнейшее увеличение времени выдержки прерывателя в состоянии «открыто» приведет к уменьшению производительности импульсного струйного аппарата.

Заключение

• 1.    Получена закономерность изменения скорости на срезе сопла импульсного эжектора с учетом введенных допущений (жидкость несжимаема, открытие канала происходит мгновенно). Показано, что удельная энергия перепада давления на сопле затрачивается сначала на разгон жидкости, а потом на стационарное истечение.

• 2.    Получены зависимости скорости движения жидкого снаряда от времени открытия сопла, анализ графиков этих зависимостей позволяет определить оптимальное время открытия задвижки для получения максимально возможной скорости движения и, как следствие, энергии, передаваемой жидким снарядам.

• 3.    Разработана методика для определения оптимального времени истечения жидкости через сопло.

Список литература