Расчет оптимальных пересечений фотоннокристаллических волноводов методом передаточной матрицы

Фотонными кристаллами называются периодические диэлектрические структуры, имеющие "запретную зону" (band gap), т.е. не пропускающие свет в определенном частотном диапазоне [1]. Предложено много оптических устройств на базе таких структур [2]. В частности, при создании интегральных оптических микросхем из-за стремления к миниатюризации возникает необходимость работать с пересечениями фотоннокристаллических волноводов (ФКВ). Эффективность пересечений волноводов является важной характеристикой работы интегральной оптической микросхемы. В целях упрощения технологического производства таких структур, их, как правило, делают двумерными. Распространение света в ФКВ ограничивается структурой фотонного кристалла в одном измерении и эффектом полного отражения в другом. В данной работе рассматривается пересечение ФКВ только под прямым углом. Однако это не является серьезным ограничением, т.к. известно, что ФКВ могут изгибаться под прямым углом на площади не сколько квадратных длин волн практически без потерь энергии.

Для расчета электромагнитного (ЭМ) поля в диэлектрических структурах используются три основных подхода [3]. При первом из них в результате расчета получаются непосредственно отсчеты ЭМ поля. Так ра- ботает, например, метод конечных разностей. При втором подходе искомыми являются коэффициенты разложения ЭМ поля по определенному базису, например, по плоским волнам. Третий подход является "гибридным". В этом случае расчетная зона разбивается на ячейки. Затем рассчитывается передаточная матрица, связывающая коэффициенты разложения ЭМ поля с одной стороны ячейки с коэффициентами разложения с другой стороны. Поэтому методы, принадлежащие к группе "гибридных" методов, часто называют методами передаточной матрицы (МПМ). МПМ требуют значительно меньших затрат машинного времени по сравнению с методами первых двух групп. Как правило, МПМ используют, когда исследуемая диэлектрическая структура может быть разбита на зоны, для которых легко найти передаточную матрицу, например, аналитическими методами [4]. В данной работе показано, что МПМ может использоваться для расчета ЭМ поля в сложной диэлектрической структуре, в которой присутствуют не только элементы с кусочнопостоянной функцией диэлектрической проницаемости (ФДП), но и элементы с непрерывно изменяющейся ФДП.

Вычислительный метод

Электромагнитные (ЭМ) поля удовлетворяют уравнениям Максвелла. Для диэлектрических сред, в отсутствии внешних токов и зарядов, уравнения Максвелла записываются в виде [5]:

Vx E =	д B -d7
Vx H =	д D д t

V- D = 0

V- B = 0

Материальные уравнения для линейной среды записываются в виде:

D ( r ) = e ( r ) E ( r )

.

B ( r ) = д ( r ) H ( r )

Для инвариантных по координате z сред, т. е . таких, где выполняется условие £ = £ ( x , у ), и, следовательно, де/ д z = 0, волновое уравнение для поперечных компонент электрического вектора ЭМ-поля записывается в виде:

V,2 E tx

д f 1 г-⁵ к ² 1 д x [ к ^{2 E}x д x J

( к ² - в ’ E x =

Чтобы найти константу распространения в в каждом инвариантном по координате z слое, рассмотрим слой, состоящий из M участков толщиной d _i и коэффициентом преломления n _i в каждом (рис.1). Тогда для n -й моды, распространяющейся вдоль оси z в i -м участке, можно записать выражение для электрического поля (ТЕ-поляризация):

Er in ⁽ x , у , z ) = ur y^Ein ⁽ x ^{) eX}P ⁽ i ^e „^Z ) , ⁽⁶⁾

где u ^r _y - единичный вектор по координате y .

Уравнение (5) преобразуется к виду:

dyE# - ( в , ² - к² E (. x ) = 0,    (7)

dx где к = 2nni /Л - волновое число.

Общее решение уравнения (7) представляется в виде суммы двух плоских волн, распространяющихся в противоположных направлениях относительно координаты x :

E in ^{( x} ) = A in exp t i/ in ⁽ x ^- x i ^{)] +}

⁺ B in ^exP ^[- i/ in ⁽ x ^- x i ^)]         ,      ⁽⁸⁾

д f 1     дк ² 1

E.

дx к    ду

V /

^{V 2} E ⁺r^f F E y T" 1⁺ д у V к    ду J

t

y

д f 1 д ^д к ² 1

ду к2 Ex дx

V /

( к ’ — в ² E =

, (4)

1/2   2пп где к = w(£u) = —— и V2 Л

д ²     д ²

д x ² д у ²

Аналогичные соотношения можно записать для магнитного вектора H .

Для ЭМ полей, у которых вектора E или H параллельны плоскостям xz или yz , и для областей с кусочно-по стоянным коэффициентом преломления задача нахождения модовых функций может быть сведена к нахождению собственных функций в следующей задаче:

Рис.1. Слой диэлектрической структуры с кусочно-постоянным показателем преломления

V 2 E = ( в ² - к ² ) е .

V 2 H = ( в ² - к ² ) н"

границе между соседними участками:

A n expa n d ⁾⁺ B in ^exP ^(- iY in d i ) =

= ^Ai + 1 n ^{+ B}i + 1 n

Y n ^[ A in exP ^{( i} Y n d i ) - Bin ^exp ⁽ - iY in d i ^)] =

= Y i + 1 n ( A i + 1 n - B i + 1 n ) .                          (9)

воположном направлении - B

Переходя к матричным обозначениям, получим:

A₊m + 1 n

в

.Bi + 1 n J

= T in

A iⁿ

в in

,

где

in ₂

1 + A n^ exp O' Y in d , ) I ^{1 -}— ^e xP ⁽- Y d , )

Y , ₊ l

Y , + i.

1 - A n^ exP ^{( i} Y in d_l) I ^{1 +} — ^ex P ^(- i Y in d i)

Y + n )

Y + n )

В случае идеально отражающих стенок получаем дисперсионное уравнение для оп-

ределения P _n :

A Mn

в

Mn J

A Mn + B Mn = 0

Пусть исследуемая нами двумерная структура периодична по оси z с периодом p . Тогда, в соответствии с теоремой Блоха [6], решения соответствующих волновых уравнений можно записать в виде:

U kz ( z ) = l"¹^ ( z ),       (13)

где U - любая из компонент ЭМ поля, u_{k z} ( z ) - периодичная функция с периодом p . Различные решения U - соответствуют различным волновым векторам k _z . Выражение (13) можно записать в виде:

U k_z ( p) =      u (0).         (14)

Представив ЭМ поле в виде разложения по N модам, получим систему уравнений размера 2 N x 2 N, т.к. учитываются коэффициенты мод, распространяющихся в положительном направлении оси z - A и в проти-

где T - передаточная матрица периода диэлектрической структуры.

Тогда собственные значения X матрицы T связаны с волновым вектором k _z следующим соотношением

X = l ^- ik z ^p

Рассчитываемые значения k _z ограничены размером первой зоны Брюллиена [7] для одномерных периодических структур

-

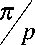
< ^kz

Из найденных 2 N значений k _z отбираем N значений с положительной вещественной частью. Оставшиеся N значений k _z имеют отрицательную вещественную часть, равную по модулю соответствующим значениям отобранных N значений k _z .

Передаточную матрицу T можно получить, используя соотношения для прошедшей и отраженной волн на границе каждого слоя.

A i + 1 = T ,.+ 1 ■ A i + R i + 1, i ■ B i + 1

B i = R i ,.+ 1 ■ A i + T + 1, i ■ B i + 1  ’

где T , i _{+ 1} и T _{i+ 1} ,_i - коэффициенты пропускания на границе между i и i + 1 слоями для прямой и обратной ЭМ волны, соответственно. Соответствующие коэффициенты отражения обозначены как R _{i , i + 1} и R _{i + 1, i} .

С помощью матричных преобразований матрица T представляется в виде:

A +1

B i+1

x

Т

T i , i +1

R .+H

■

гр -1

T i +1, i

■

R .i+1

-1

i +1, i i , i +1

-1

^Ti +1, i ^{■ R}i +1, i

-1

T i +1, i

x

A _ A, B i J=r-[ B i

Распространение ЕМ-волны в инвариантном по координате z слое описывается в виде:

Ail

A

Bid

DR -0-V A i l

0 ' Di ⁺ i ¹

B

= Di"

Г A i l B i

± где Di - диагональная матрица

— ¹

r r r r T

T ^{, i + 1} = 2l ( E ‘.n , H^1^ + E +^n , , h.^ I

1                            к , (24)

r rT r r n‘,‘ +1 _ _L|/f Ы \ - F H \ VT‘:+1

R 2 I \ E ‘' +!, ” ’ ^H i kk/ E n\ n ’ ^H i +1, k/ \T

D . ±

^exP ⁽± i0_od_M +i )

0L exP(± 'Mi,! +1 )

0 LL 0

0          "

^exP ⁽± ‘ ^ M d , i +1 )

Здесь в _т — константа распространения m -й моды.

Передаточная матрица T для всей структуры представляется в виде

M

T = П D i r . .          (22)

i = 0

Так как матрица T , как правило, является сингулярной, то нахождение матрицы обратной к передаточной матрице T выполнялось методом декомпозиции сингулярного значения [8].

Можно показать [9], что для непоглощающих структур набор модовых функций (6) является полным. Кроме этого, модовые функции (6) являются ортогональными.

Коэффициенты T , . + ! , T _+u , R i + i и R +_u из выражений (18) находятся из условия непрерывности тангенциальных компонент n -й моды на границе между слоями I и ‘ + 1. Если n -я мода падает на границу между слоями ‘ и ‘ + 1 из слоя г, то верны соотношения

где

(E ‘n , H i+и¹) = JJ ( E ‘ . n x H_w ) ■ a z dS . ⁽²5) S

Здесь интегрирование ведется по поверхности, которая ограничивает исследуемую структуру. Для рассматриваемого нами двумерного случая вычисление интегралов (13) упрощается из-за того, что E _{, n} и H _{, k} являются скалярами и выражаются простыми соотношениями типа (8).

Для того, чтобы загасить паразитные отражения от границ расчетной области в данной работе использовался метод PML (Perfectly Matched Layers) первоначально предложенный в [10]. Для реализации метода PML была выбрана его интерпретация, при которой гасящий слой имеет комплексную толщину [11]:

xc = j f ( x ) dx%,            (26)

где f ( x ) выбрана в виде:

f (x) =

1 + b,, если x e PML

1, иначе

^r              k , n ^r               k , n ^r

,, n + Z и+1 i, k Z i,+1 ‘+1, k k               k              . (23)

^r             k , n ^r              k , n ^r

H i,n Z RT ‘' + 1 E i\k = Z T ,i' + 1 H ‘ + 1, k kk

Используя свойство ортогональности модовых функций, можно получить соотношения для матриц T ‘' ^{+ 1} и R ‘ ^{+ 1}, в которых каждый n -й столбец состоит из коэффициентов T k + 1 и R i ^ , соответственно

здесь b - параметр регулирующий, наряду с толщиной PML, уровень гашения паразитных отражений.

При использовании PML корни дисперсионного уравнения (12) становятся комплексными. Для поиска комплексных корней уравнения (12) использовался метод спуска, описанный в статье [12].

Анализ метода вычислений

Таким образом, оптическое моделирование фотонного кристалла, выполненное в данной работе, включает следующие этапы:

1. Разбиение расчетной зоны, соответствующей исследуемой диэлектрической

структуре, на слои, перпендикулярные направлению распространения света.

• 2.    Вычисление констант распространения модовых функций в каждом слое. Для этого необходимо найти корни дисперсионного уравнения.

• 3.    Вычисление передаточной матрицы, соответствующей исследуемой диэлектрической структуре. Для этого используется сшивка разложения ЭМ поля по модовым функциям на границах слоев.

• 4.    Расчет ЭМ поля внутри исследуемой структуры, используя передаточную матрицу и коэффициенты разложения падающего ЭМ поля по модовым функциям.

Описанный метод численного решения уравнений Максвелла можно отнести к "гибридным" методам, если пользоваться классификацией, приведенной в начале статьи. В публикациях [13, 14] авторов данной работы использовался похожий метод численного решения уравнений Максвелла для моделирования дифракционного оптического элемента (ДОЭ). Тем не менее, схожесть этих методов ограничивается первым этапом из вышеприведенного списка. В работах [13, 14] использовалось разложение ЭМ поля по плоским волнам, а не по модовым функциям. В общем случае, использование модовых функций позволяет сократить количество коэффициентов разложения ЭМ поля, не снижая точности представления. Чтобы рассчитать прохождение ЭМ поля через слой диэлектрика, в работах [13, 14] решалась система дифференциальных уравнений, для чего использовались или метод экспоненциальной матрицы в двумерном случае или метод Рунге-Кутты в трехмерном. При разложении ЭМ поля по модовым функциям расчет прохождения ЭМ поля через слой диэлектрика выполняется путем умножения каждого коэффициента разложения ЭМ поля на величину, постоянную для каждого слоя. Кроме этого, в работах [13, 14] не использовался метод "PML" для гашения паразитных отражений от границ расчетной области. Это препятствует точному моделированию исследуемой структуры в открытом простран- стве. Отметим, что выполненное в данной работе моделирование работы диэлектрической структуры в центре пересечения двух фотоннокристаллических волноводов можно интерпретировать как исследование ДОЭ, квантованного по 34 уровням.

Результаты численного моделирования

В численном эксперименте рассчитывалось ЭМ поле в двумерной диэлектрической структуре, представленной на рис.2. Стержни состоят из материала GaAs с коэффициентом преломления n = 3,4 . Период структуры связан с диаметром стержня соотношением d/a =1/4. Известно [2], что данная структура имеет "запретную зону" в частотном диапазоне для TE-поляризации.

На рис.3 показано распределение компоненты E _x вектора электрического поля в пересечении двух волноводов со следующими параметрами: a = 0,6 мкм, d = 0,15 мкм, r =0, л = 1,5 мкм, Размеры расчетной зоны без использования PML 6,6 мкм на 4,8 мкм, с использованием PML 6,6 мкм на 8,8 мкм. Использовалось разложение ЭМ поля по 60 модовым функциям. Слева на рис.3 показано распределение в случае металлических стенок, справа ‒ со слоем PML толщиной 4 мкм, с параметром b = 0,1 . Визуализируемая область в обоих случаях имеет размеры 6,6 мкм на 4,8 мкм. Время расчета ЭМ поля в каждом случае составило около минуты на компьютере с процессором Pentium III 800МГц.

a

a

d

• •   •   •   •   • r • е е • е

Рис.2. Пересечение двух волноводов в двумерном фотонном кристалле

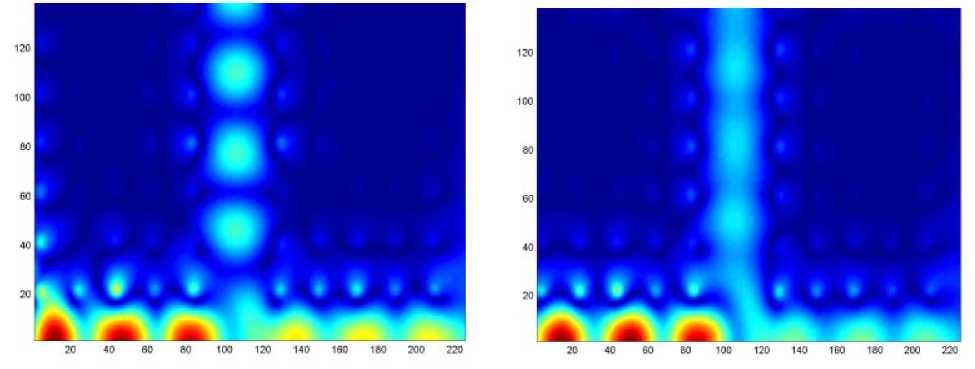
а)                                                      б)

Рис.3. Распределение электрического поля в отсутствии неоднородности в центре пересечения волноводов с идеально отражающими стенками (а) и при использовании PML (б)

На рис.4 показано распределение компоненты Ex вектора электрического поля при различных значениях r. Диэлектрическая неоднородность в центре пересечения ФКВ была разбита на 34 слоя, одинаковых по толщине и перпендикулярных направлению распространения волны. Для r = 2,5a количество прошедшей энергии составило 97%, для r = 2,7a - 81%, для r = 2,9a - 35%, для r = 3,0a - 19%.

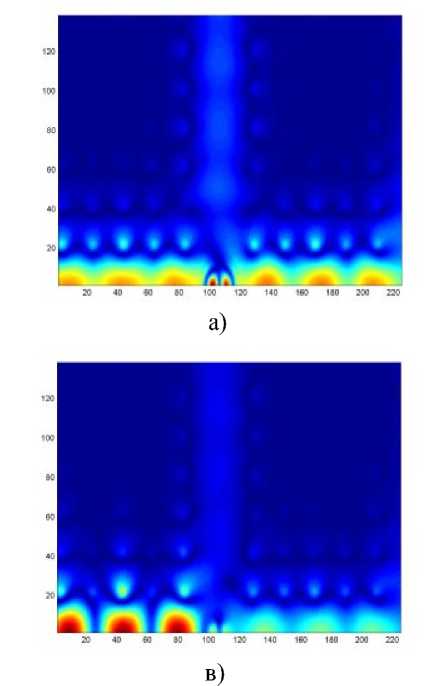
Рис.4. Распределение электрического поля с неоднородностью в центре пересечения волноводов; размер неоднородности (а) r = 2,5 a , (б) r = 2,7 a , (в) r = 2,9 a , (г) r = 3,0 a

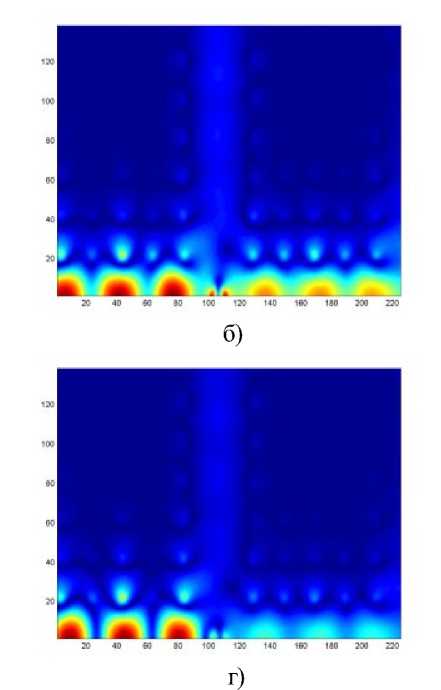
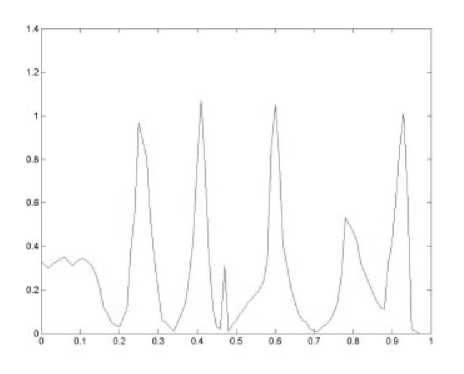
Рис.5. Зависимость количества прошедшей энергии от размера неоднородности

Отметим, что при всех значениях r утечка энергии в перекрестный волновод не превышает нескольких процентов. Эта особенность соответствует результату, полученному в [15], и может быть объяснена резонансной природой взаимодействия неоднородности в центре пересечения волноводов с ЭМ полем. При создании реального оптического устройства количество энергии, ушедшей в перекрестный волновод, является более важной характеристикой, чем количество энергии, прошедшей прямо, т.к. операция фильтрации сигнала является значительно более сложной, чем операция его усиления.

На рис.5 показана зависимость количества энергии, прошедшей через пересечение по горизонтальному волноводу, от размера неоднородности в центре пересечения волноводов. Размер неоднородности дан в относительных к периоду фотонного кристалла единицах.

Выводы

В данной работе показано, что использование метода передаточной матрицы для расчета электромагнитного поля в окрестности диэлектрической неоднородности, расположенной в пересечении двух фотоннокристаллических волноводов, позволяет получать достоверные результаты. Данные результаты соответствуют результатам, полученным в [15] с помощью метода конечных разностей, который требует значительно больших затрат машинного времени по сравнению с методом передаточной матрицы.