Расчет периода раскачки утфеля раствором сахарозы в вакуум-аппарате
Автор: Славянский А.А., Семенов Е.В., Лебедева Н.Н., Антипов С.Т.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Биотехнология, бионанотехнология и технология сахаристых продуктов
Статья в выпуске: 4 (70), 2016 года.
Бесплатный доступ
Важным и ответственным элементом в управлении технологическим потоком производства кристаллического сахара товарных кондиций является период времени обогащения утфеля в виду его обессахаривания в процессе кристаллообразования в вакуум-аппарате. Хотя в настоящее время предложен и внедрен в промышленность, в том числе и в качестве интерфейсного сопровождения процесса, ряд способов, в реальных условиях сахарного производства во многих случаях приходится прибегать к услугам опытного варщика. Очевидно, что в любом случае необходимо располагать зависящими от объемного содержания сахара в растворе данными по времени подачи сахарсодержащего раствора в вакуум-аппарат. Касательно вопроса о периоде протекания процесса обогащения обедненного сахарозой раствора интродуцируемым в эту субстанцию раствором сахарозы следует отметить, что данная проблема теоретически проработана все еще недостаточно. При этом очевидно, что в практических целях желательно иметь простые и удобные для инженерного расчета зависимости времени обработки сахаром заданного объема воды от режимных параметров процесса (требуемой концентрации раствора по сахарозе, температуре раствора, условий перемешивания и др.). Проблема количественного анализа процесса кристаллизации сахарозы в вакуум-аппарате, включая сроки обогащения межкристального раствора сиропом, периода времени обработки утфеля в целом в данном аппарате, исследовалась во многих работах. Однако вследствие своей важности для решения задачи получения товарного сахара высоких кондиций эта проблема нуждается в дальнейшем углубленном изучении. В статье с целью обоснования процесса обогащения раствора сахарозой в результате обессахаривания этой жидкостной системы в вакуум-аппарате, с позиций диффузионной теории кристаллообразования в растворе, предлагается более обоснованный, по сравнению с известными до сих пор аналогами, количественный анализ данного процесса, где в качестве коллектива кристаллов сахарозы рассматривают систему шаров, равномерно распределенных в моделирующем вакуум-аппарат объеме. На базе решения поставленной задачи получены расчетные формулы, результаты численного эксперимента отражены графическим путем.
Вакуум-аппарат, раствор сахарозы, процесс диффузии, период обработки
Короткий адрес: https://sciup.org/140229656
IDR: 140229656 | DOI: 10.20914/2310-1202-2016-4-233-237
Текст научной статьи Расчет периода раскачки утфеля раствором сахарозы в вакуум-аппарате
Одним из важных и ответственных элементов в управлении технологическим потоком производства кристаллического сахара товарных кондиций является период времени обогащения утфеля, в виду его обессахаривания в процессе кристаллообразования в вакуум-аппарате. Несмотря на то, что в настоящее время предложен и внедрен в промышленность в том числе, и в качестве интерфейсного сопровождения процесса, ряд способов, в реальных условиях сахарного производства во многих случаях приходится прибегать к услугам опытного варщика. Очевидно, что в любом случае необходимо располагать зависящими от объемного содержания сахара в растворе данными по времени подачи сахарсодержащего раствора в вакуум-аппарат.
Касательно вопроса о периоде протекания процесса обогащения обедненного сахарозой раствора интродуцируемым в эту субстанцию раствором сахарозы следует отметить, что данная проблема теоретически проработана все еще недостаточно. При этом очевидно, что в практических целях желательно иметь простые и удобные для инженерного расчета зависимости времени обработки сахаром заданного объема воды от режимных параметров процесса (требуемой концентрации раствора по сахарозе, температуре раствора, условий перемешивания и др.).
Проблема количественного анализа процесса кристаллизации сахарозы в вакуум-аппарате, включая сроки обогащения межкристального раствора сиропом, периода времени обработки утфеля в целом в данном аппарате, исследовалась в работах [1–6]. Однако вследствие своей важности для решения задачи получения товарного сахара высоких кондиций эта проблема, по нашему мнению, нуждается в дальнейшем углубленном изучении.
Ниже, с целью обоснования процесса обогащения раствора сахарозой в результате обессахаривания этой жидкостной системы в вакуум-аппарате, с позиций диффузионной теории кристаллообразования в растворе, предлагается более обоснованный, по сравнению с известными до сих пор аналогами, количественный анализ данного процесса.
Постановка и решение задачи
Пусть в некотором рабочем объеме имеют гетерогенную жидкостную систему, включающую жидкую среду и коллектив моделируемых как шары радиусом R кристаллов сахарозы. Предполагая, что шары статистически равномерно распределены в жидкости, в качестве модели процесса массопереноса от жидкой среды к шарам выбирают изолированный шар, к которому из прилегающей к нему области (R < r < L) (где r – радиальная координата, 2l – среднее расстояние между центрами шаров) подаются молекулы сахарозы (рисунок 1).
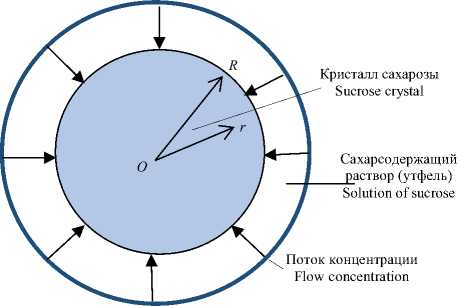
Рисунок 1. Схема к расчету процесса кристаллообразования сахарозы в утфеле
-
Figure 1. The scheme to calculation of process of grain formation of sucrose in the massecuite
При этом, если V ш и V – соответственно, суммарный объем шаров и жидкости в рабочем объеме и £ - объемная концентрация шаров в жидкостной системе, то в соответствии с принятой геометрической моделью жидкостной системы “жидкость + система шаров” половина расстояния l между двумя соседними шарами составит (рисунок 2)
l = R^xr, 0 < £ < 1. (1)
Сахарсодержащий раствор
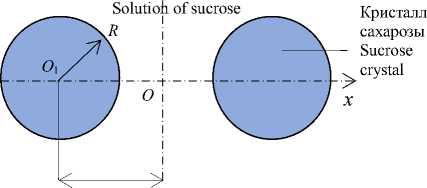
Рисунок 2. Схема к расчету процесса массопереноса сахарозы в жидкостной системе
-
Figure 2. The scheme to calculation process of a mass transfer of sucrose in liquid system
Полагают, что массоперенос к шарам от жидкой среды реализуется симметричным образом, и, кроме того, для выбранной расчетной модели, с удовлетворительной точностью выполнены все, обычно принимаемые при анализе процесса массопереноса в сплошной среде, допущения по физико-механическим свойствам изучаемого объекта.
Поток концентрации q сахарозы в направлении оси r в принятой одномерной модели массопереноса в сферической системе отсчета рассчитывают по формуле
При этом уравнение (3) по переменной u вследствие (7) сохраняет свой вид
_ 6с q=- d т, (2)
d r
1 = D d t
^d 2u 2 d u
---2 +
, d r r 6 r
где D – коэффициент диффузии, с – объемная концентрация сахарозы, r – радиальная координата.
В качестве исходного соотношения, опи-
сывающего кинетику распределения концентрации в растворе, выбирают, как обычно, отнесенное к сферическим координатам, с началом координат в центре О 1 шара, уравнение нестационарной диффузии (второй закон Фика) (рисунок 2).
— = D d t
< d 2 - 2 d -
—7 + , d r r d r
( R < r < L ) ,
В целях упрощения решения задачи начальное условие (10) заменяют его усредненным значением по прилегающей к шару области r е (R, 1)
l
3_ 3 fu(r,0)r2dr = Ас.
I R R
В свою очередь, усредняя левую часть уравнения (11) по тому же объему, принимают f |U r=dr = D^(t), l R.
где t – время.
Начальное условие по исходному распределению концентрации принимают в виде
где ф(т ) - функция, подлежащая определению.
В результате уравнение (11) заменяют приближенным
- ( r ,0) = - n ( R < r < l ), (4)
d 2u 2 d u 1 A
—— +-- = ф ( t ).
d r 2 r d r
где с п – концентрация пересыщенного раствора.
Граничное условие на поверхности шара
- ( R , t ) = - н (0 < t <« ), (5)
где с н – концентрация сахарозы на поверхности шара (кристалла сахарозы).
Граничное условие симметричности поля концентрации между соседними шарами dC(l,t) = 0 (0 dr где l связана с R зависимостью (1). Хотя решение задачи (2)–(6) известно, оно малопригодно для практических расчетов, так как имеет вид ряда. Поэтому, как поступают в некоторых случаях, ниже применяют приближенный метод решения данной задачи, аналогичный методу осреднения. С этой целью, как обычно, предварительно проводят замену переменной с = u + сн,(7) в результате чего граничные условия (5), (6) становятся однородными по переменной u – приведенной концентрации u(R, t) = 0,(8) du (l, t) —= 0, 0 dr Начальное условие вследствие (4) принимает форму u(r,0) = A-(R < r < l), где A - = - п - - н > 0 - перепад концентрации в начальный момент времени t = 0. Так как правая часть уравнения (14) зависит лишь от t, то, интегрируя его дважды по r, находят u(r, t) = D + D2 /r + r2ф(t)/6,(15) где D1, D2 – произвольные величины, зависящие от t. Согласуя (15) с граничными условиями (8), (9), получают R 3+2l3/ Di =--7TT- ^(t), D2 = V ^(t) 6 R3 и поэтому вместо (15) имеют u(r, t)=y(r )ф( t X где v(r r) = R3 + 213 6 R l3 +---1. 3 r6 Подставляя (16) в (13), приходят к дифференциальному уравнению относительно искомой функцииф , 3 1p3 JV(r) drr 2 dr = D^( t x l - Rdt или А d^ = Dф(18) dt где l А = 3_ 3 f^(r)r2dr, lR l связано с R и концентрацией с зависимостью (1). Интегрируя (18), получают ф. t) = D3 ехр (Dt / А),(20) где D3 – произвольная постоянная. Поэтому, в соответствии с (16), (20) имеют u ( r, t ) = D3^( r )exP( D ), 3А где ф(r) задана по (17). С целью определить D3, подставляют (21) в (12) 1l з_ з J D3^(r)r dr = Ac, l RR откуда приходят к соотношению D3 А = Ac, (22) где А определяют по (20). В результате чего, вследствие (21), (22) окончательно имеют Ac Dt. u(r,!) = ^/( r )exP(^) АА Как видно, что найденное по (23) выражение приведенной концентрации u(r, t) имеет простую и удобную для количественного и качественного анализа мультипликативную форму. А именно, приведенная концентрация пропорциональна перепаду концентрации Ac, и, поскольку, согласно расчету, А < 0, ф(r) < 0 при R < r < l, в соответствии с (7), (23) концентрация жидкостной среды положительна, убывает по экспоненте с течением времени t и, тем быстрее, чем больше коэффициент диффузии D. Если входящее в (23) выражение ^(r) заменить его усредненным значением ф = A согласно (19), то (23) упрощается и принимает вид Dt u = A с exp(—), А (l3- R3)Aс Q-пред = limTQ = ----—3----. (27) 3R Тогда если значение периода времени т между двумя раскачками утфеля пересыщенным раствором определяют исходя из того, чтобы выраженный в долях Qпред коэффициент пересыщения к рассчитывался по отношению Q /Qnped = к , (28) откуда, исходя из (26)–(28), получают расчетное значение периода (мин) между двумя раскачками утфеля A т =----ln(1 - к), (29) 60D где А вычисляют по (19). Численный эксперимент Рассматривается пример расчета периода времени между двумя раскачками утфеля сахарсодержащим раствором. Коэффициент диффузии принимаем D = 2^10 - 10 м2/с, что примерно соответствует значению данного коэффициента при температуре раствора 70 °С. Полагали, что кристаллы сахарозы в растворе монодисперсны, диаметр частиц d = 20…40 мкм, объемная концентрация частиц £ = 40.. .50%. По выбранным таким образом исходным параметрам, на базе (29), параметрические по размеру d частиц и их объемной концентрации Е, рассчитаны графические зависимости периода т между двумя раскачками утфеля от коэффициента пересыщения к (рисунок 3). где Aс = сп — сн. На базе количественного анализа (24) судят о распределении концентрации в обессахариваемом утфеле в заданный период времени. Поток концентрации сахарозы от жидкостной среды (утфеля) к поверхности шара (кристалла сахара) согласно (2), (23) (с точностью до знака) вычисляют по зависимости (м/с) q (t) = D ^^(R,!) оr D =--X 3A R3 - l3 А Г Dt x----—Ac ■ exp R2 ( A к Рисунок 3. Зависимости периода т(мин) между двумя раскачками утфеля от коэффициента пересыщения к для различных значений диаметра d (мкм) и объемной концентрации ^ (%) частиц (d = 20 мкм: 1 - ^ = 40, 2 - ^ = 50%; d = 40 мкм: 3 - ^ = 40,4 - ^ = 50%) Полный удельный объем Q сахарозы, подводимый к единице поверхности шара за время Т, получают, интегрируя (25) по данному временному интервалу Т (м3/м2) Т Q = J q (t ) dT = (l3- R3)Aс 3R2 , (26) В соответствии с (26) предельное значение подводимого к единице поверхности шара объема сахарозы составляет Figure 3. Dependences of the period т (min.) between two swings massecuite from supersaturation coefficient к for various values of diameter d (mcm) and volume concentration ^ (%) of particles (d = 20 мкм: 1 - ^ = 40, 2 - ^ = 50%; d = 40 мкм: 3 - ^ = 40, 4 - ^ = 50%) Из вида графиков рисунка 3 выявляется согласие полученных результатов количественного моделирования рассматриваемого процесса с физическим смыслом исследуемого явления. А именно, естественное увеличение периода τ раскачки в вакуум-аппарате когда возрастает коэффициент пересыщения κ (все кривые рисунок 3). Кроме того, отмечается уменьшение периода раскачки для частиц одного размера вместе с ростом их концентрации (кривые 2 и 4 расположены, соответственно, ниже кривых 1 и 3), а также в случае, когда при одинаковой концентрации ξ увеличивается размер частиц.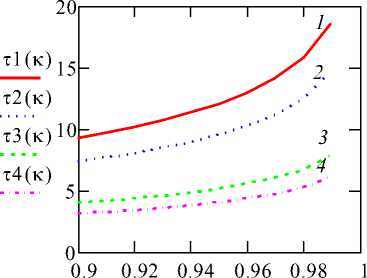

Список литературы Расчет периода раскачки утфеля раствором сахарозы в вакуум-аппарате
- Saska M. Modelling crystallization and inclusion formation in sucrose crystals//Zuckerindustrie. 2011. V. 113. № 3. Р. 224-229.
- Tuzhilkin V., Urazbayeva K., Alibekov R. Semicontinuos sugar crystallization//Jour. of industrial technology and engineering. 2012. № 2 (3). P. 11-18.
- Beckmann W. Crystallization: basic concepts and industrial applications. Weincheim: Wiley-VCH Verlag GmbH & Co, 2013. 346 p.
- Гнездилова А.И, Червецов В.В. Интенсификация процессов кристаллизации при производстве молочных продуктов. Воронеж: "Издательство Ритм", 2011. 196 с.
- Семенов Е.В., Славянский А.А., Сергеева Е.А., Щитова Т.А. Особенности диффузионного процесса кристаллизации Сахарозы//Сахар. 2013. № 3. С. 46-50.
- Тужилкин В.И., Прокофьев Е.Н., Коваленок В.А., Клемешов Д.А. и др. Технология полунепрерывной кристаллизации Сахара//Сахар. 2014. № 2. С. 30-33.


