Расчет процессов релаксации при обезвоживании рыбы

На интенсивность процесса массопере-носа оказывают влияние режимные параметры, геометрические размеры тела, его химический состав. Исследователями установлено [1], что скорость движения сушильного агента выше двух метров в секунду не оказывает влияния на интенсивность обезвоживания после достижения первой критической влажности на кривых кинетики сушки. Это явление можно объяснить тем, что процесс испарения влаги с поверхности в сушильную среду протекает с большей скоростью, чем перенос влаги из центра к поверхности рыбы. По мере обезвоживания мясо рыбы уплотняется. При этом размер пор капилляров уменьшается в шесть – десять раз. Особенно это ярко проявляется в приповерхностном слое, который граничит с сушильным агентом. Решение дифференциальных уравнений тепломассопереноса осуществлялось в основном при граничных условиях первого рода [2, 3], хотя зачастую тепловая обработка рыбного сырья происходит при граничных условиях третьего рода. Многие исследователи и производственники пытались восстановить влагопроводные свойства в приповерхностном слое рыбы за счет периодического прекращения воздействия

Вестник ВГУИТ/Proceedings of VSUET, № 3, на объект сушильного агента или увлажнения его поверхности мелко диспергированными частицами воды, или ведения процесса при постоянном значении коэффициента активности воды (мягкие режимы сушки). Другие рекомендуют вести процесс обезвоживания, используя жесткие режимы сушки. На наш взгляд, является перспективным восстановление влагопроводных свойств рыбы путём периодической остановки процесса сушки для релаксации поверхностного слоя рыбы в сочетании с достаточно жёсткими режимами обезвоживания.

• 1.1    Цель и задачи исследований

До настоящего времени процесс релаксации влаги в рыбе мало изучен. Не выявлены его закономерности, способствующие не только снижению продолжительности, но и затратам энергии при производстве рыбных продуктов. На основании изложенного целью работы является изучение и выявление основных закономерностей внутреннего массопереноса влаги в процессах, протекающих при малых значениях критерия Био. Для достижения поставленной цели необходимо решить следующие задачи:

• 1.   Разработать методику изучения про

• 2.    Выявить основные закономерности, протекающие при перераспределении влаги внутри объекта обезвоживания.

• 3.    Разработать    энергоэкономичные

цесса релаксации.

способы обезвоживания рыбы в комбинации воздействия на объект сушильного агента и периодическом восстановлении его влагопроводных свойств.

• 1.2    Описание процесса релаксации

Количество влаги dM 1 , перемещающейся из внутренних слоёв тела к поверхности за время d т , можно записать, воспользовавшись законом Фурье. Перенос влаги из центра тела к его поверхности равен:

dM 1 = —Am 1 dF (d w / dn ) dt ,       (1)

где X m 1 - удельный коэффициент массопровод-ности, кг / (м - % - с); F - поверхность тела, м²; w - содержание влаги в теле, %; т - продолжительность, с; ( d w/дг ) 1 - производная по направлению, перпендикулярному к поверхности F (градиент влажности), % / м.

В процессе обезвоживания поверхностные слои уплотняются. Поэтому уплотненные слои оказывают перемещению влаги большее сопротивление, чем остальные внутренние части рыбы. Перенос влаги через них описывается следующим дифференциальным уравнением:

dM ₂ = —Am ₂ dF (d w / d n )₂ dt ,      (2)

где X m 2 - удельный коэффициент массопроводно-сти сухого слоя, остальные обозначения известны.

Определенное количество влаги предается от поверхности тела к окружающей среде:

^dM 3 = ^в т ⁽ w n — w e ) ^dFdt ,         ⁽³⁾

где в m - удельный коэффициент массоотдачи от поверхности тела в окружающую среду, кг / (м² - % - с); W n - содержание воды на поверхности тела, %; w₆ - содержание воды в сушильном агенте, %.

При отсутствии движения сушильного агента в период релаксации коэффициент в m существенно уменьшается, стремясь к нулю. Тогда dM 3 = 0. Принимая во внимание, что dM 1 = dM 2 , получим следующее выражение:

— Am , dF ( dw / dn ) dt«—Am ₂ dF ( dw / dn )₂ dt (4)

Разделим обе части уравнения на dFdT ,

—Am_t ( dw / dn ) « — Am ( dw / dn )₂     (5)

Для удобства анализа перейдем к одной пространственной координате и будем рассматривать случай неограниченной пластины толщиной 2 1 . Из уравнения (5) следует, что в процессе перераспределения влаги релаксационные кривые имеют общую точку с одинаковой влажностью, в которой они пересекаются. Общая точка с постоянной влажностью после достаточно глубокого обезвоживания перед релаксацией располагается вблизи внутренней границы «сухого слоя». Коэффициент удельной влагопроводности X m 2 по мере насыщения поверхностного слоя влагой увеличивается более значимо, чем уменьшается X m 1 . В таком случае общая точка будет постепенно перемещаться вверх и вправо на кривых динамики обезвоживания от точки А до точки А 1 (рисунок 1). Разницу в динамике изменения X m 1 и X m 2 можно объяснить тем, что объем приповерхностного сухого слоя значительно меньше объема слоя с высокими влагопроводными свойствами. Поворачиваясь вокруг общей точки одинаковой влажности, левая часть кривых динамики релаксации поднимается вверх, а правая часть опускается вниз. Точку одинаковой влажности на кривых динамики релаксации назовем точкой поворота. Через довольно продолжительное время обе части достигнут среднеобъемной влажности.

• 1.3    Особенности расчета процессов релаксации

образца; w – среднеобъёмная влажность, на значение которой оказывают влияние следующие

В более ранних работах нами разработана методика расчета процессов обезвоживания и параметры:

w = у ( т ,N,X p , W o , 5 / m ),

релаксации влаги численными методами с учетов влияния химического состава, геометрических размеров объектов обработки и режимных параметров процессов сушки [4, 5]. По этой методике в течение периода релаксации расчет влажности объекта обработки ведется от центра к поверхности, т. е. задачей расчета является определение влажности на поверхности и построение кривых динамики обезвоживания. Влажность на поверхности определяется из следующего выражения:

n - 1

Wn = W-2 w, (6) i=1 n где wп – влажность на поверхности образца; wi – влажность в узлах сетки, за исключением влажности на поверхности; n – количество отрезков, на которые разбита половина толщины где N – скорость обезвоживания в первый период сушки; Xp – жесткость режима процесса обезвоживания; w0 – начальная влажность объекта обработки; s/m – удельная поверхность объекта обработки.

Условием расчёта процесса релаксации является наличие кривой динамики сушки в момент прекращения подачи сушильного агента. Однако кривые динамики релаксации объекта сушки, полученные расчетом методом сеток, в приповерхностой зоне имеют выпуклость вниз. Это показывает, что влажность на поверхности растёт несколько быстрей, чем в приповерхностной зоне, т. е. в данном случае допущение dM 3 = 0 приводит к несколько искажённым результатам при расчетах процесса релаксации с использованием численных методов.

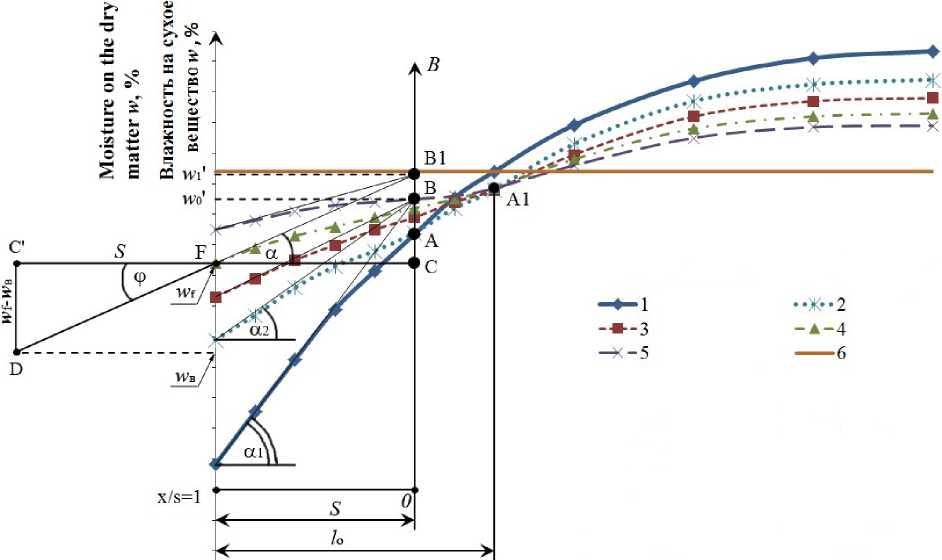
x//=l

Полугол шина /, м Half thickness I, in

Рисунок 1. Кривые динамики релаксации рыбы: 1 – кривая на момент начала релаксации; 2 – кривая на момент релаксации 0,5 часа; 3 – кривая на момент релаксации 1 час; 4 – кривая на момент релаксации 1,5 часа; 5 – кривая на момент релаксации 2 часа; 6 – среднее влагосодержание в образце рыбы

Figure 1. The curves of the dynamics relaxation fish: 1 – the curve at the beginning of the relaxation; 2 – relaxation curve at the time of 0,5 hours, 3 – relaxation curve at the time of 1 hour; 4 – curve at the time of relaxation of 1,5 hours; 5 – curve at the time of relaxation 2 hours; 6 – average moisture level in a sample of fish

По мере увлажнения приповерхностного слоя со стороны притока влаги из центральных слоёв, частично восстанавливаются влагопроводные свойства, вместе с тем влага частично испаряется с поверхности. Поэтому кривая динамики релаксации должна быть направлена выпуклостью вверх.

Для уменьшения погрешности определения влажности на поверхности объекта релаксации предпочтительно использовать данные расчёта численными методами только для нахождения двух кривых динамики распределения влаги непосредственно после обезвоживания, т. е. в начальный момент релаксации при τ р = 0 и в заключительный момент этого периода релаксации при τ р = τ 1 , например τ р = 0,5 часа. В дальнейших расчетах применяем решение дифференциального уравнения второго порядка с граничными условиями третьего рода для неограниченной пластины, которое выглядит следующим образом:

n

⁹ ( X т ) = Е A i e" ^ Fo • cos ( ^ i xIR ) ⁽⁸⁾ i = 1

здесь n – количество равноотстоящих точек на той или иной части кривой динамики релаксации ( n = 4 – 7); A i – постоянный коэффициент, свой для каждого члена ряда (не зависящий ни от координат, ни от времени τ); Fo – критерий Фурье, Fo = D т / R 2 , где D - коэффициент диффузии влаги; μ i – корни характеристического уравнения:

θ

^{( X} .^{т )}

w0 - w

⁰            ( X •- )

w o^- w ( Hi ) ’

9, A = ^{( X} ,^{t )}

w - - w           w' - w

¹ .*“. ⁹( X .t)                       ,

w, - w, л      ( . )   w-- w, л

1          ( Hi )                               n         ( Hi )

где w - . w , . w - - значение влажности в точках поворота для начальной, первой и последующих групп релаксационных кривых (рисунок 1), пересекающихся в одной общей для группы кривых точке: B, B i , B n ¹; w ( _х , т ) - искомая влажность образца в какой-либо его точке через промежуток времени, равный т = Т р ; w ( Hi ) - влажность образца в соответствующей точке предыдущей релаксационной кривой.

Для правой части от точки А (рисунок 1) кривой динамики релаксации искомое значение компоненты в безразмерном виде выглядит следующим образом:

θ

⁽ x^{, т} )

w - wo

(X т)      0 Д_

, 9(X.т) = w, Л - w0

(Hi)

w - w,'

( X т )           ¹

w, А - w,0

( ^Hi )          ¹

9/ i = ^{( X} . ^т )

w - w0

(X т )         n w, A - w'

( Hi )         n

μ

ctgи=Bi

Так как при расчетах численным методом

изначально заложены граничные условия третьего рода, то их можно будет учесть и в дальнейших расчетах, подбирая в решении дифференциального уравнения второго порядка коэффициенты А i и μ i таким образом, чтобы значения построенной численным методом кривой динамики релаксации совпали с таковой при τ р = τ 1 , построенной на основе представленных ниже уравнений.

При расчете левой половины кривой динамики релаксации R = S , где S толщина зоны релаксации. Для правой части кривой динамики релаксации от точек А и А 1 значение R = l , здесь l половина толщины образца (рисунок 1). При Fo ≥ 0,5 достаточно воспользоваться только одним корнем μ i выражения (8). Использование выражения (8) для расчёта левой половины от точки А кривой динамики в процессе релаксации:

Из уравнения (8) следует, что для релаксационных процессов распределения влажности по толщине «сухого слоя» для разных моментов времени τ свойственны симметричные кривые, монотонно возрастающие от наружной поверхности «сухого слоя» образца к его внутренней поверхности (рисунок 1). Касательные, проведенные к кривым динамики релаксации, проходят через одну точку В . Если касательные к кривым пересекаются, то эти кривые должны сойтись в какой-то точке А .

Исходными данными для расчета служили левые и правые части кривых 1 и 2 (рисунок 1). Эти кривые получены расчётным путем с использованием метода сеток. Точки на кривой 1 являлись исходными для нахождения A i и μ i в уравнении (8).

Для расчёта релаксации рыбы в приповерхностном «сухом слое» (слева от точки А ) использовалась величина S в качестве определяющего размера. Критерий Fo находили для левой и правой частей релаксационных кривых из выражения: Fo = D т / 5 2 . Определение коэффициентов по-тенциалопроводности D (коэффициентов диффузии влаги) производили по методике, разработанной авторами ранее [4].

¹ Общие точки пересечения релаксационных кривых В 2 , В 3 ,…, Вn на рис.1 не показаны. Они характерны для релаксационных процессов после достаточно глубокого обезвоживания рыбы.

Значение D определяли для приповерхностного «сухого слоя». Подбирая значения A i и μ i , добивались близкого совпадения значений, полученых из уравнения (8), с таковыми на первой релаксационной кривой 2 (рисунок 1) при τ р = 0,5 часа. В этом случае сохраняются в дальнейших расчётах граничные условия третьего рода, которые были учтены в расчетах процессов обезвоживания численными методами. Продолжительность релаксации τ р = 0,5 часа является минимально-возможной в реальных промышленных установках с точки зрения рационального управления системой автоматического поддержания заданных технологических режимов. При достаточно длительном обезвоживании пересечение кривых 1 и 2 (точка А ) находится вблизи внутренней границы приповерхностного «сухого слоя». Далее строили касательную к левой части кривой 1. На касательной отмечали точку В в месте пересечения касательной и вертикальной линии, проходящей через точку А . Касательные, проведенные к двум – трем релаксационным кривым, пересекаются в точке В , а кривые 1, 2 и 3 проходят через точку А (точка поворота релаксационных кривых). Касательные, проведенные к кривым 4 и 5, имеют уже другую точку пересечения В 1 и, как следствие, сами кривые пересеклись в точке А 1, которая находится правее и выше точки А .

Значение влажностей w ‘ о и w ' 1 в точках В и В 1 (рисунок 1) являются начальными значениями при определении безразмерной величины θ. При расчете процесса релаксации длительностью 2,5 – 3 часа возможно, что количество точек « В » возрастет до трех или четырех. В этом случае в расчетах 6 меньшее значения влажности w ‘ о в точке В заменяют на большое в точках В1 или В2 , а, возможно, и В3 . Следовательно, точка поворота перемещается вправо и вверх к точкам А 2, А 3 (на рисунке 1 не показаны).

В реальности точка поворота А по мере релаксации плавно перемещается вправо и вверх (от точки А до точки А 1). Чем меньше отношение wср/wк2 (отношение средней влажности к влажности второй критической точки) или wср/w0 (отношение средней влажности к начальной влажности рыбы), тем меньше значение ординаты точки А 1 отличается от таковой в точке А и наоборот. При больших значениях wср/wк2 или wср/w0 может наблюдаться существенное удаление точки А 1 от точки А . Это явление объясняется тем, что при сравнительно высоких влажностях по мере релаксации быстрее восстанавливаются влагопроводные свойства так называемого приповерхностного сухого слоя, и процесс релаксации происходит при меньших значениях Aw = w‘о - wf, постепенно достигая равновесного состояния как в правой, так и в левой от точки А частях кривой динамики релаксации.

При бесконечно большом времени релаксации кривые динамики релаксации достигнут средней влажности образца. Тангенс угла а наклона касательных (рисунок 1) равен:

tg ^a =

B 1 C

FC

дю дx

С другой стороны, продолжив касательную влево от точки F, очевидно, что tga = tgф, tgф = (wf - w,) / S, где wf – содержание воды на поверхности рыбы (рисунок 1).

Для случая, когда вся влага, пройдя от центра к поверхности, полностью испарится в окружающую среду, основное уравнение мас-соотдачи в дифференциальном виде выглядит следующим образом:

-km (dW 1 дx) = bm (W/ — we )

или dw / дx = tga = ^ф = (w/ - W,) /S = Ьт I km (w - W,). Отсюда следует, что S = pm/Xm.

Таким образом:

= ( ^W / — w , )/( ^ m /^в m ) = ( w f — w , ) • Bi/^{1  ( 12)}

x = 1

д w д x

Последнее выражение позволяет находить критерии Био расчётным путём как для процессов обезвоживания, так и для процессов релаксации влаги.

Рассмотрим вариант, в котором большая часть влаги остается в левой части образца для восстановления влагопроводных свойств последнего, а часть – испаряется в окружающую среду. Обозначим долю влаги, испарившейся с поверхности: a = dM 3 / dM 2 . В этом случае основное уравнение массоотдачи в дифференциальном виде примет вид:

akm 2(дw I дx) = Ьт (W/ — we ) (13)

После небольших преобразований получим следующее выражение:

= ( w / - w e )/ ( a ^ ^Xm 2 /Р m ) =

= ( ^W/ — w e ) • ^Bi /( a • ^l )

Последнее выражение можно использовать для расчета критерия Bi , когда значение коэффициента влагообмена p m > 0.

На рисунке 2 представлен расчет процесса релаксации в соответствии с методическим подходом, изложенным выше. Результаты расчета с использованием численных методов практически совпадают с аналитическим решением дифференциального уравнения второго порядка с граничными условиями третьего рода.

Характер кривых динамики релаксации, постро енных с помощью аналитического решения диф ференциального уравнения второго порядка, со ответствует таковому, найденному путем постро ения кривых на основе эксперимента.

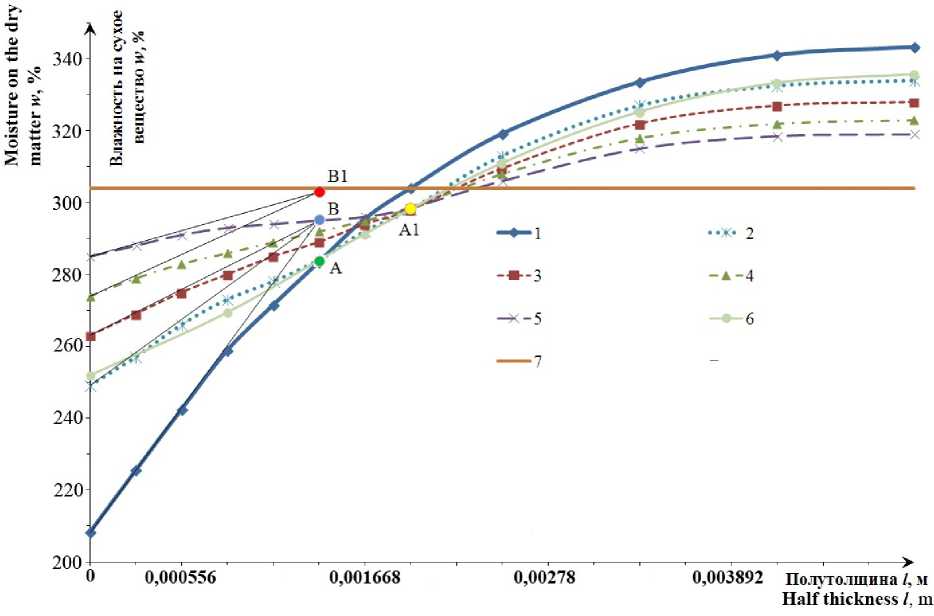
Рисунок 2. Кривые динамики обезвоживания и релаксации камбалы-ерша: 1 – кривая на момент начала релаксации; 2 – кривая на момент релаксации 0,5 часа; 3 – кривая на момент релаксации 1 час; 4 – кривая на момент релаксации 1,5 часа; 5 – кривая на момент релаксации 2 часа; 6 – кривая на момент релаксации 0,5 часа, построенная методом сеток; 7 – среднее влагосодержание в образце рыбы

Figure 2. The curves of the dynamics of dehydration and relaxation rough dab: 1 – the curve at the beginning of the relaxation; 2 – relaxation curve at the time of 0,5 hours, 3 – relaxation curve at the time of 1 hr; 4 – curve at the time of relaxation of 1,5 hours; 5 – curve at the time of relaxation 2 hours; 6 is a curve at the time of 0,5 hours of relaxation constructed by numerical method; 7 – average moisture level in a sample of fish

Заключение

Заложены теоретические основы изучения механизма релаксации приповерхностного сухого слоя рыбы посредством анализа кривых динамики распределения влаги, полученных