Расчет пространственных мод оптических волноводов с неоднородным поперечным сечением методом согласованных синусоидальных мод

Для расчета векторных или скалярных пространственных мод оптических волноводов и волокон с неоднородным поперечным сечением применяются несколько методов: техника поперечного резонанса [1], метод согласованных синусоидальных мод [2, 3], метод линий [4], метод распространения собственных мод [5].

Также расчет электромагнитных полей в неоднородных по сечению волноводах можно проводить с помощью более универсальных расчетных методов: конечных элементов [6, 7], разностного решения уравнений Максвелла [8, 9] или распространения пучка [10, 11].

Поскольку результат расчета электромагнитных полей в волноводах зависит от возбуждающего поля, то для характеристики самого волновода требуется найти весь спектр возможных пространственных мод. Поэтому в данной работе для расчета мод неоднородных оптических волноводов выбран метод согласованных синусоидальных мод (ССМ) [2, 3], который наиболее органично подходит для анализа диэлектрических волноводов с кусочнопостоянным заполнением поперечного сечения.

ССМ-метод основан на представлении решения для пространственной моды в виде суперпозиции локальных синусоидальных мод, которые являются собственными модами однородных частей волновода с прямоугольным сечением.

1. Описание метода согласованных синусоидальных мод

Рассмотрим метод отыскания поля в волноводе неоднородного поперечного сечения. Для иллюстрации будем использовать волновод, изображенный на рис. 1. Предположим, что сечение волновода может быть разбито на N строк и M столбцов так, чтобы ни одна из прямоугольных ячеек этого разбиения не содержала неоднородностей (рис. 1).

Таким образом, каждой ячейке, находящейся на пресечении n - ой строки и m - го столбца, можно поставить в соответствие некоторое значение диэлектрической проницаемости ε ^(m,n) , постоянное для данной ячейки. Пусть оси координат располагаются, как показано на рис. 1. Тогда толщина n - ой строки:

d yn ) = y ⁽ n ^{+ 1)} - y ⁽ n ) ,

где и n

y ⁽ n ) - координата плоскости, разделяющей n - 1 строки. Аналогично, толщина m - го столбца

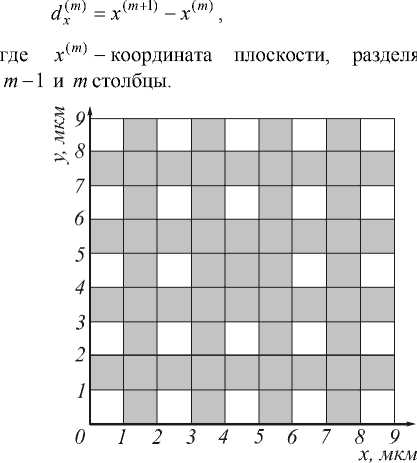
Рис. 1. Схема поперечного сечения волновода, выполненного в виде фотонного кристалла; темным цветом показаны области со значением диэлектрической проницаемости б ⁽ m ^{, n}) = 3 , светлым - с б ^{( ,} ) = 1

Таким образом, диэлектрическая проницаемость в m - ом столбце есть функция

б ⁽ m ) ( y ) = б ⁽ m , ⁿ) для y ^{( n}) <  y < y ^{( n + 1)} .           (3)

На краях сечения подразумевается наличие электрических или магнитных стенок, обеспечивающих равенство нулю функции поля или ее производной при x = 0 , y = 0, x = x ⁽M ^{+ 1)} , y = y ⁽N ^{+ 1)} .

Рассмотрим уравнение Гельмгольца для монохроматического света:

v ² E ( x , y , z ) + k 0 б ( x , y ) E ( x , y , z ) = 0,          (4)

здесь E(x, y, z) – проекция на продольную ось z вектора электрической напряженности электромаг- нитного поля; k0 = —, где Xo - длина волны в ва-X о кууме; s(x, y) - диэлектрическая проницаемость среды, зависящая от пространственных координат, в общем случае есть зависимость и от координаты z , но мы считаем сечение волновода постоянным.

Решение уравнения (4) будем искать в виде

E = u ( x ) ф ( y ) e ^ik z ^z

.

Подставим (5) в уравнение (4):

V ² ( u ( x ) ф ( y ) e   ) + k ₀ ² s ( x , y ) u ( x ) ф ( y ) e    = 0,

V ² ( u ( x ) ф ( y )) e ^{- lk}-^z - k z u ( x ) ф ( y ) e - ^k - ^z + + k ₀ ² s ( x , y ) u ( x ) ф ( y ) e ^{- ik} z ^z = 0,

V ² ( u ( x ) ф ( y )) - kz² u ( x ) ф ( y ) + + k o² e ( x , y ) u ( x ) ф ( y ) = 0, w( x ) ф ( y ) +ф ( y ) u ( x ) + + ( k 0 ² e ( x , y ) - k z ²) u ( x ) ф ( y ) = 0.

Далее будем опускать аргументы у, u и ф , чтобы записи были более короткими. Итак, мы получили и ф + ф u + ( k 0 s ( x , y ) - k .°) u ф = 0.               (6)

Проведем разделение переменных, поделим (6)

на u ф :

ф + u +(k о2е( x, y)- k?) = 0 ф u или

• •

“ + (k0s(x, y) - kz) =  “

ф

Положим u = - kx,(9)

u теперь (8) можно разделить на два уравнения

[ф + ⁽ k о^{2 s (} x , y ) ^- k z ^- k ²^ = °

[ u + k x u = 0.

Обозначим kz + kx = k,° , (11) тогда ф +(к°2 s(x, y)- kkto ° (12) .u + (kk - kz2)u = 0.

Первое уравнение в (10) и (12) будет далее решаться только при s ( x , y ) = s ⁽ m ) ( y ) (17).

Введем еще одно обозначение k о2 s( x, y) - kk = ky,                           (13)

то есть теперь ko2s( x, y) = kx2 + ky + kz2.                        (14)

Значит k x , k y , k_z - проекции на соответствующие оси координат волнового вектора k , модуль которого равен | k | = -^k 02 s ( x , y ) .

Решение системы уравнений (12) зависит от функции s ( x , y ) и не может быть получено в общем виде в алгебраической форме. Поэтому далее рассмотрим способ приближенного решения.

В скалярном случае поле в m - м столбце можно представить в виде

ю

^ ⁽ x , y ) = Е u km ^{) ( x ) ф} km ^{) (} y )’                  ⁽¹⁵⁾

k = 1

здесь опущен множитель e - ik ^z Z . Каждая из множества функций u km ) ( x ) удовлетворяет второму, а каждая из ф k^m ) ( y ) - первому уравнению системы (12) в столбце m , то есть для x ^{( m} ) <  x <  x ^{( m + 1)} и y ⁽¹⁾ <  y <  y ⁽ N ^{+ 1)} , причем в данной области все эти функции являются непрерывными вместе с первыми производными. Будем называть u k^m ) ( x ) и ф km ) ( y ) локальными модами, а индекс k определяет номер локальной моды и напрямую связан с введенной соотношением (11) величиной k_k , их взаимосвязь будет показана далее.

Вычисление локальных синусоидальных мод Рассмотрим уравнение ф + (k o2s( x, y) - kk;)ф = 0.                       (16)

Так как s ( x , y ) = s ^{( m} ) ( y ), то (16) можно решать в каждом столбце отдельно, независимо от других столбцов. Итак, в некотором столбце (индекс m опускаем) (16) примет вид:

ф + ( k 0² s ( y ) - k k ²)ф = 0,     (17)

здесь s ( y ) = s ⁽ n ) = const для y ⁽ n ) <  y <  y ⁽ n ^{+ 1)} . Решение (17) в n - ой строке между y ^{( n )} и y ^{( n + 1)} будет иметь вид:

^{ф (} y ) =

^{( n} , l )

фп,l) cos[kyn)(y - y(n))] + ^a-sin[kyn)(y - y(n))], (18) (n) ky где kyn) =Vs(n) k°2 - kk ,(19)

ф<п, l) =ф( y(n) + 0)(20а)

• -    нижнее или левое значение функции ф ( y ) в строке n ;

ф(ап,1 > =ф (y(n > + 0)(20б)

• -    нижнее или левое значение производной ф ( y ) в строке n .

Следует отметить, что поскольку kyn) может принимать только действительные или чисто мнимые значения, то функция ф(y), определяемая (18), будет вещественной для любых действительных фSn,1) и фО’,1). Аналогично (20а) и (20б) можно оп- ределить правые значения ф(у) и ее производной ф(у) в строке n :

P ⁽ i ¹ =

cos[ k ¹ d ⁽ i ) ]

- sin[ k ai ) d ^{( i )} ] k ai )

sin[ k ¹ d ⁽ i ) ]/ k у ) cos[ k y) d ⁽ i ) ]

, (24)

ф ⁽” ^, r > = ф ( у ⁽ ” ^{+ 1)} - 0),

(20в)

ф an ^, r ) =ф ( у ⁽ ” ^{+ 1)}

— 0).

(20г)

Q ^{( i )} =

cos[ k у ) d ⁽ i ) ] sin[ k ^i ) d ⁽ i ) ] k у )

- sin[ k у ) d ⁽ i ) ]/ k у ) cos[ k ^i ) d ⁽ i ) ]

. (25)

Иллюстрация фS”-r1

ф О” ^{, 1 1}

,

расположения ф S” ^{, 1 1} ,

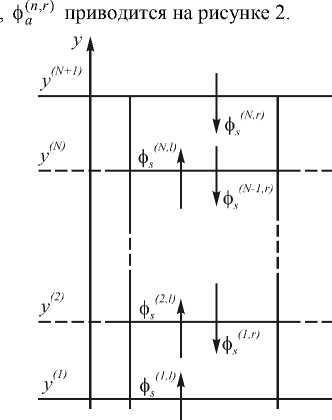
Рис. 2. Схема обозначения полей на границах разбиения сечения волновода

Таким образом, чтобы решить (17) нужно определить значение k k и 2 N - 2 - констант ф S” ^{, 1 1} и ф О’ ^{, 1 1} , так чтобы функция ф ( у ) удовлетворяла (17) и

Очевидна справедливость равенств

ф S” ^, r ) . ф⁽; ^, r )

= p ⁽ n )

ф S” ^{, 11} . ф О” ^{, 1} )

ф S” ^{, 11}

. ф⁽ а” ^{, 11}

= Q ⁽ ” )

ф S” ^, r ) . ф О” ^, r )

которые равносильны (22) и (23). Используя матрицы P ^{( i )} и Q ^{( i )} , можно легко выражать значения

ф S7 ^, r ) . ф^' r )

рез

через

ф (^ r ¹ . ф а^-; r ¹

краевым    условиям:

[ф ( у ⁽¹⁾ ) = 0,

[ф ( у ⁽ N ^{+ 1)} ) = 0

или

ф( у(1)) = 0, соответственно для электрических ф (у(N+1)) = 0,

или магнитных стенок.

Требование непрерывности решения (17) и его производной приводит к следующим соотношениям:

ф ( ” ' r ¹ =ф S” ^{+ 1} l ¹

(21а)

ф <" ^, r ¹ =ф <" ^{+ 1, 1 1}

(21б)

ф Sⁱ , ¹¹ . ф а- , ¹¹

i <  j , и значения

i >  j . Так, например,

^ф S , 1 _ р( ” '1 р( ” ' - 11 р1 ^ф s , 1 . ф О” ', r ¹ ]’                           [ф О¹'^{1 1}

ф S” '⁺1, ¹¹ . ф О” ⁴¹, ¹¹

= Q ( ” '+ 11 Q ( ” '+² 1

- Q ⁽ N ¹

ф S^j , ^{1 1} . ф a^j , ¹¹

ф S^N , r ¹ . ф a^N , r ¹

че-

Для вычисления k_k , точнее квадрата k ^2 , поскольку только квадрат фигурирует в приведенных выше формулах, воспользуемся следующим методом. Определим функцию

А ⁽ ” ^( k k ²) = ф S” ', r ¹ ф ⁽”' ^{+ 11 1} -ф 0”^ r ¹ ф S” ^¹, ¹ ) ,       (28)

где ”'е (1, N), значения фa”,r1, ф a”,r1 и фS”+1,11, ф (”+1,11 вычисляются с использованием (26) и (27) и потому зависят от kk . Нули функции А(”)(k^ и есть искомые значения. Поиск нулей (28) равносилен решению характеристического уравнения ф S”' r1 ф (””'+1,11 -ф a”' r1 ф S”41,11 = 0, (29) причем ”' может быть произвольным числом из интервала (1, N) .

Кроме того, для ф S” ^{, 1 1} , ф ⁽ _О ” ^{, 1 1} , ф S” ^, r ¹ , ф О” ^, r ¹ справедливы равенства:

( ” , 1 )

ф(”,r1 =ф(n,1) cos[k(”1d(”)] + ^a— sin[k(”1d(”)], (22а) s            s               у                   (n)           у фОr1 =ф(а”,11cos^a”1d(”)]-фS”,11k(”1sinka,”1d(”)], (22б)

⁽ n , r )

ф ( ” , I ) =ф ( ” , r ) cos[ k a ” ¹ d ⁽ ” ⁾ ] -^^y- sin[ k a ” ¹ d ⁽ ” ⁾ ] , (23а) ky

ф ⁽ _а ” , ^{1 1} =ф О” , r ) cos k у” ¹ d ⁽ ” ) ] +ф S” , ^{1 1} k у” ) sin k a” ¹ d ⁽ ” ⁾ ]. (23б)

Введем в рассмотрение матрицы, детерминант которых равен единице

Можно убедиться, что зависимость решения (29) от ненулевых значений ф?’11 ’ .фО1’11 _ и ■ф SN, r1 ■ .ф aN, r1 _ от- сутствует, поэтому, решая (29), в случае электриче-

ских	стенок			можно	считать	■ф S1’1 1 - .ф О1,1 1 _	=	■ 0 . 1 .
-ф SN z1 - Ver 1 J	=	■ 0 [ 1 J	,	а в случае	магнитных -	■ф S1’1 1 - .ф О1,1 1 _	=	■ 1 . 0 .
"ф SN z 1 -		■ 1 -
_ф а^г 1 _	=	[ 0 J	.

Различных значений k k , удовлетворяющих (29), бесконечно много, но все они находятся на интервале ( -« , k ^ax ], где их можно отсортировать по убыванию. Каждое из значений k k определяет локальную моду ф ⁽m ) ( у ) в m - м столбце сечения волновода. Точность построения поля по формуле (15) зависит от количества используемых локальных мод. Но как бы много мы их не взяли (как бы много корней уравнения (29) не нашли), это всегда будет некоторое конечное число K .

Когда все K значений k _k ² найдены, нас интересуют константы ф ⁽П ’ ¹ ) , ф ⁽П ’ ¹ ) , ф ⁽П ’ r ) , ф '," ^, r ) , их можно найти из условия нормировки функции ф ( у )

на единицу:

у <  N +D

7 ^ + 1)-> j * ^{2 (} У ⁾ dy = ^{L             (30)}

y y у ⁽ )

Здесь

у ^{( N + 1)}                    N у ⁽ n ^{+ 1)}

I = j ф 2( у) dУ — £ jф 2( у) dУ = у <’>                      n =1 у < " )

£ [у^ С- ¹ о ; ⁾ -Ф Sⁿ ' r W⁾ ) + d n-    ⁾ ) ² + () ² )].

П = 1 ^{2( k}y )                                 ^{2                 к}у

Когда kk известны, значение к(") для каждой строки может быть рассчитано по формуле (19). Принимая во внимание соотношения ф Sn’ r) = р( Ор(n'-1)...p1 ф S1’11 . ф an', r) J"                        [ф O11)

n ' — 1, N , (31)

ф <ⁿ • ¹ ) . ф On ' ¹ )

ф ( ^{п - 1,} r ) . ф⁽; ^{- 1,} r )

n — 2, N ,

значение интеграла I можно считать функцией от ф ^¹’¹ ) или ф О^1,1 ) в зависимости от типа стенок. Тогда (30) решается стандартными методами и имеет ровно два действительных корня, отличающихся только знаком, любой из них может быть выбран в качестве значения ф ⁽¹’ ¹ ) (или ф Х ^{1, 1} ) ), остальные константы рассчитываются с использованием (31), (32) и найденного значения.

Действуя по вышеописанному алгоритму, для каждого столбца сечения волновода можно найти K значений k_k ² и для каждого из них сконструировать функцию ф (у ) , которая будет удовлетворять (17) при данном k k .

Сшивка локальных мод

Рассмотрим уравнение

(mm )2 л2;,/m uk (x) + (kk - kz )uk (x) = 0, (33) здесь -km)(x) является k - ой модой в столбце m, соответствующей kkm) также как фkm)(у). Уравне- ние (33) аналогично (17), соответственно его решение имеет вид

(m)           (m,1)         (m)( uk (x) — usk cos[kxk (x x )] +

( m , 1 )

sin[ kXm)(x - x(m))],(34)

kxk где kXm)—vkkm)2 - kZ(35)

и

• - Sm,1) — -km)(X(m) + 0),(36)

• - am,1) — - km)(x(m) + 0).(37)

Аналогичным образом вводятся

• - Sm,r) — -km)(x(m+1) - 0),(38)

• - (k, r) — - km)(x(m+1) - 0).(39)

Разница между уравнениями (33) и (17) состоит в том, что решением (33) является не одна непрерывная функция вида (34), а набор из M определенных и непрерывных на соответствующих интервалах функций. Формула (34) объединяет их в одну, ( m , 1 )      ( m , r )

но разрывную функцию, поэтому для - Sk , - Sk и ( m , 1 )      ( m , r )

-Ok , -Ok    соотношения, аналогичные (21), не выполняются, тем не менее, справедливы равенства n (m,1) uak

u

( m , r ) ak

z,⁽ m ) ⁽ m , 1 )             7 ⁽ m ) ⁽ m , r )

kxk ^-sk      + kxk ^-sk        (40а)

tariff^{( m} )^^{( m} )1   sinf^^{( m} )^^{( m} )1 ,

^Ldn( kkx dx ) ^sin( kkx dx )

( m ) ( m , 1 )               ( m ) ( m , r )

kxk ^-sk + kxk ^-sk      , (40б)

qinf^(m)J(m)^   tariffm)J(m)^ , sin( kkx dx )   Idn( kkx dx )

Поскольку (40) выполняются для всех k — 1, K удобно использовать матричную запись. Введем диагональные матрицы T ^{( m} ) и S ^{( m} ) размерности K х K с диагональными элементами

( m )      ( m )           ( m ) ( m )

^T kk ^— k xk / taⁿ⁽ k kx d x ), ^(41а)

( m )      ( m )           ( m ) ( m )

S kk ^{— k} _x k / ^{sln( k} k _x d x ^{). (41б)} Теперь ⁽⁴⁰⁾

примут вид

U m , ¹ ) _— - t ^{( m} ) u< ^m , ¹ ) + s ^{( m} ) u< ^m , r )

U<^m , r ) _— - s ^{( m} ) u< ^m , ¹ ) + t ^{( m} ) u< ^m , ^r )

Здесь

.

u Om , ¹ ) — [ - О m , ¹¹ u O^m , ^r ) — [ - am , ^r ) u S^m , ¹ ) — [ - Sm , ¹¹ u S^m , ^r ) — [ - Sm , ^r )

( m , 1 )

^- a 2

( m , r )

^- a 2

( m , 1 )

- S 2

( m , r )

- S 2

U ( m , ¹ ) f

• ^- aK ^] ,

⁽ m , r ) i T

^- aK ^] ,

( m , 1 ) ] ^r

• ^- sK ^] ,

( m , r ) i T

^- sK ^] .

Рассмотрим теперь интеграл перекрытия

< ^f . I f 2 >^— ^a N + 1 T

у < ^{N + l)}

—(iy  j f.(у) f г(у) dv, у     у (1)

(42а)

(42б)

составим матрицу из элементов вида (43), где в качестве f _ и f , будут использованы ранее найденные моды ф^ ) ( у )

u S¹¹ ) = [0 о - 0] ^т , и <^м , r ) = [0 0 - 0] ^т -

Op^l’^   ф W) >  ,

получится квадратная матрица O ^{( m} ’ ^{m )} размера K x K , обладающая очевидным свойством

( O ( m , m ') ) T = о ( m ', m )

-

Кроме того, так как ортогональные функции ф к" ) ( у ) нормированы, то матрица O ^{( m} ’ ^m ) равна еди-

Если стенки магнитные, то матрица т ⁽¹⁾ должна быть заменена на т ⁽¹⁾* с диагональными элементами т к ¹* =- k x P tan( k xk dx^), а матрица т ^{( м} ) - на матрицу т ^{( м} )* , т к )* = - k Xk^м ) tan( к<_хк ^м ) d <^м ) ) -

Задачу, описываемую соотношениями (49), в общем виде можно представить как

Л ( к, )U = 0,

ничной, и каждая из матриц тарной-

O ^{( m} ’ ^{m )} является уни-

где матрица Л ( к , ) состоит из ( м - 1) x ( м - 1)

O ( m , m ') O ( m ', m ) =

-

Для конечных значений размерности K x K соотношение (46) выполняется довольно точно только для соседних столбцов, то есть если m ' = m + 1 или m ' = m - 1- Из ортонормированности функций Ф к" ) ( У ) и требования непрерывности поля £ ( x , у ) (вместе с производными первого порядка) следует выполнение условий

K

„(m,к) _ V/)(m,m+1).,(m+1,1) usk   = ^ okp    usp p=1

K

„(",к) _ V/9(","+ 1).,(m+1,1) uak  = ^ Okp    uap p=1

Или в матричной записи

U< m , r ) = O ( m , m + 1) u< m + 1, 1 )

( m , r )      ( m , m + 1) ( m + 1, 1 )

U_a   = O     U_a    -

,

-

(47а)

(47б)

(48а)

(48б)

Объединяя (42) и (48) и исключая U ^^m ’ ¹ ) , U am , r ) , u (m , r ) , получим

( о ( m , m - 1) т ( m - 1) о ( m - 1, m ) ₊ т ( m ) ) u( m , 1 ) =

O ( m , m

' -

1) s ( m - 1) U ( m - 1, 1 ) + s ( m ) o ( " , " + 1) u ( m + 1, 1 )

(49а)

для

для

2 <  m <  M ;

( O ⁽У) т ⁽¹⁾ O ⁽¹2 + ти ¹ ) _ S ⁽²⁾ OU ¹¹ m = 2, когда M >  2 ;

( o ( м , м - 1) т ( м - 1) o ( м - 1, м ) + т ( м) )U^ m , 1 ) _

O ( м , м - 1) ^ ( м - 1) и( м - 1, 1 )

(49б)

(49в)

для

m = M -

В простейшем случае, когда M = 2 , получаем

( O ⁽¹,²⁾ _т ⁽²⁾ + _т ⁽¹⁾ O ⁽1,2⁾ ) U ( 2, l ) _ 0.

(49г)

Соотношения (49) выполняются в случае электрических стенок, когда краевые условия имеют вид

ков, размерности K x K матрицы имеет вид:

каждый- Структура

бло- этой

Л ( к , ) =

’ A ⁽²⁾

B ⁽³⁾

о

C ⁽²⁾

A ⁽³⁾

B ⁽⁴⁾

о

C ⁽³⁾

A ⁽⁴⁾

о

о

_C (4)

о о о

о о о

о о о

о о о

- (51)

о о

о о

о о

о о

о о

B ( м - 1) о

A ( м - 1) B ^{( м} )

C ( м - 1) A ^{( м} )

Здесь

A ( "  ) = O ( " , " - 1) т ( " - 1) O ( " - 1, " ) + т ( "  )

_B ( m ) _{= - O} ( m , m - 1) _s ( m - 1) _,

_C ( m ) _{= - s} ( m ) _O ( m , m - 1)

О - нулевая матрица размерности K x K -

В (50) вектор

u =

U ( 2, ¹¹

и ⁽³, ¹¹

s

и (^м , ¹¹

-

Мы получили задачу (50), которая имеет только тривиальное решение U = 0 , если det( Л ( к , )) * 0 -Так как матрица Л ( к , ) зависит от параметра, мы можем подобрать значение к_, таким образом, что хотя бы одно из собственных чисел Л ( к_, ) будет нулевым, тогда, полагая U равным собственному вектору, соответствующему нулевому собственному числу, мы удовлетворим (50)- Для поиска таких значений к_, предлагается следующий метод-

Возьмем произвольный вектор V с ненулевыми компонентами, например, единичный- Будем решать уравнение

Л ( к , )U ' = V (56) относительно U ' - Очевидно, для разных значений параметра к_, будем получать разные решения уравнения (56)- Определим функцию f ( к , ) = 1/ U ' _p , где U ' _p есть p - ая компонента вектора U ' - В окре-

стности искомых значений k_z функция f ( k_z ) является непрерывной функцией скалярного аргумента, и ее нули есть искомые k_z .

Поиск нулей f (kz) осуществляется стандарт- ными методами. Для каждого из найденных kz мат- рица Л(kz) становится числовой, определив собственный вектор U , соответствующий ее нулевому собственному числу, мы получаем некоторые из значений констант, необходимых для конструирования K функций вида (34). Остальные можно найти, воспользовавшись соотношениями (42) и (48), в следующем порядке.

Для m = M

U_s ^{( M , l )} известно как часть U ;

• 1)    Если стенки электрические, то

U -^M , r) = [0 0       0] T , тогда

U -M , l ) =— т ⁽ M ^ M , l ) и u aM , r ) =— _s ⁽ M ) U M , l ) ;

• 2)    Если стенки магнитные, то

U(M,r) = [0 0       0]T a [              ] , тогда

U M , l ) = ( t ⁽ M ⁾ ) ^- 1 ( — ( т ⁽ M ) ) 2 ₊ ( s ⁽ M ) ) ² ) u^^{M , 1} )

u S^M , r ) = ( S ⁽ M ) ) ^{- 1} ( u a M , l ) + T ⁽ M U M , l ) ).

Для 1 <  m < M

• 1)    U*-m ^, r ) = O ⁽ m ^, m ^{+ 1)} U^m ^{+ 1,} l ) ■

  и

  
  

• 2)    U*- m ’ r ) = O ( m ’ m + 1) U ^m + 1’ l ) "

• 3)    U⁽™ ’ l ) = ( S ^{( m} ) ) ^{- 1} ( - U a^m ’ r ) + T ^{( m)} u (^m ’ r ) )

этот пункт выполняется только для m = 1, так как для других значений m вектор Us(m,l) известен, как часть собственного вектора U ;

• 4)    u<^m ’¹) = - т^(m )u^^m ’ l) + S^(m)U⁽-^m ’ r)

  .

  
  
2.    Численные результаты

Таким образом, для каждого значения kz можно сконструировать K мод вида (34), объединив их с K модами вида (18) (они одни и те же для разных kz ) по формуле (15), получаем поле в сечении вол- новода, распространяющееся в направлении оси z , с проекцией kz волнового вектора на эту ось.

Ниже приводятся результаты расчетов , проведенных при помощи математического пакета Matlab 6.0, для волновода, сечение которого изображено на рис. 1.

Как следует из рис. 1, сечение волновода было разбито на M = 9 столбцов и N = 9 строк. В качестве граничного условия использовалось условие равенства нулю поля на краях сечения. Вычисления проводились для излучения с длиной волны в вакууме Х0 = 1,3 мкм. Для каждого столбца сечения было получено по K = 40 значений k^km)2, удовлетворяющих характеристическому уравнению вида (29) (таблица 1). Для каж- дого из этих значений была построена локальная мода Фк'”)(У). Различных решений задачи (50) в данном случае оказалось более ста. Распределения интенсивности в сечении первых нескольких мод с наибольшими значениями параметра kz показаны на рис. 3.

Табл. 1. Корни характеристического уравнения (29) для трех различных типов столбцов сечения волновода

m k	1,3,7,9	2,4,6,8	5
1	64,2383	69,9582	69,1702
2	64,2343	69,5926	66,4472
3	64,2292	68,9834	64,2318
4	64,2251	68,1305	64,2317
5	47,6200	67,0339	61,9325
6	47,5711	65,6935	55,6687
7	47,5101	64,1095	47,7458
8	47,4602	62,2818	47,5406
9	25,9664	60,2104	47,5308
10	25,3814	57,8953	38,3052
11	24,5208	55,3365	27,9266
12	23,6360	52,5341	25,0060
13	15,6980	49,4879	24,8084
14	14,5517	46,1980	18,2359
15	12,5823	42,6645	15,0959
16	10,2083	38,8872	13,4231
17	8,0763	34,8663	10,9748
18	-0,6847	5,6230	1,3531
19	-3,7939	-0,1038	-3,9389
20	-7,7667	-6,0743	-7,1449
21	-12,2263	-12,2885	-12,4743
22	-16,8233	-18,7464	-17,0784
23	-22,1979	-25,4480	-22,5124
24	-27,5639	-32,3933	-28,6909
25	-33,0938	-39,5822	-33,4829
26	-38,4214	-47,0149	-40,7911
27	-47,9161	-54,6913	-49,0486
28	-53,3655	-62,6113	-55,0483
29	-59,8437	-70,7751	-61,6515
30	-66,6876	-79,1825	-68,6689
31	-73,1481	-87,8336	-75,7737
32	-81,8960	-96,7285	-84,6344
33	-89,5239	-105,8670	-92,5589
34	-97,4445	-115,2492	-100,1193
35	-105,4019	-124,8751	-109,8932
36	-115,8679	-134,7447	-119,1908
37	-123,7581	-144,8580	-127,5402
38	-132,6166	-155,2150	-136,7245
39	-141,7554	-165,8157	-145,7534
40	-150,5108	-176,6601	-155,6022

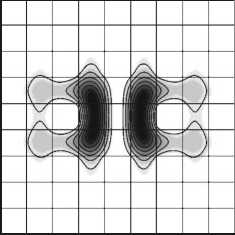
Из рис. 3 видно, что основная мода данного волновода, выполненного в виде фотонного кристалла, т.е. в виде периодически расположенных участков с высоким и низким показателями преломления, сосредоточена в осевом сердечнике размером 3 х 3 мкм.

| 9'

^8

/

0   1 2 3 4 5 6 7 8 9

X. MKM

а i 9'

S

0 123456789

X, JMK.M

б

в

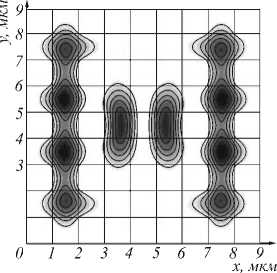
г

Рис. 3. Распределение поперечной интенсивности первых четырех мод неоднородного сечения волновода (рис. 1) с константой распространения: k z = 8,2786 мкм^а), k z = 8,1681 мкм^-(б), k z = 8,1513 мкм"¹(в), k z = 8,1373 мкм" 1 (г)

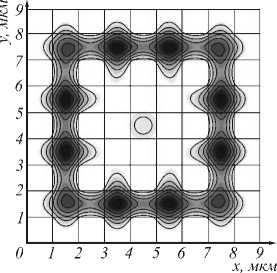
На рис. 4 показана в процентах доля энергии основной моды (рис. 3а), приходящаяся на ту или иную однородную область сечения, при этом в осевом сердечнике сосредоточено до 97%.

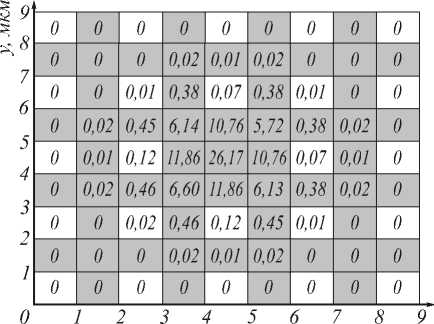
x, MKM

Рис. 4. Распределение энергии основной моды волновода (данные указаны в процентах)

Очевидно, несимметричность распределения на рис. 4 связана с погрешностями в вычислении.

Поскольку данный метод является приближенным, возникает вопрос о его сходимости. В частности о том, какое количество локальных мод нужно использовать для построения поля по формуле (15), чтобы результат был более или менее точным. То есть насколько большим должно быть число K , чтобы результат и сложность его получения были приемлемы. На рис. 5 показана зависимость получаемого значения константы распространения k _z основной моды волновода (рис. 1) от количества локальных мод в столбцах K . Из рис. 5 видно, что при К >20 K z рассчитывается с точностью до 4-го знака после после запятой.

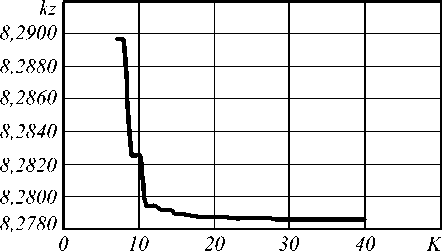
Рис. 5. Зависимость значения константы распространения k _z (мкм^-1) основной моды от количества локальных мод в столбцах K

Заключение

В работе получены следующие результаты.

• •    Предложена модернизация известного метода согласованных синусоидальных мод, применяемого для скалярного расчета модового состава неоднородных оптических волноводов, основанная на матричной форме записи характеристического уравнения.

• •    Модернизированный метод согласованных синусоидальных мод реализован с помощью программного пакета Matlab 6.0 и применен для расчета мод оптического волновода, выполненного в виде фотонного кристалла;

• •    показано, что почти вся энергия основной моды данного волновода сосредоточена в осевом сердечнике однородного сечения и не попадает в оболочку, которая представляет собой периодически расположенные однородные области с высоким и низким показателем преломления.

Работа поддержана российско-американской программой «Фундаментальные исследования и высшее образование» («BRHE»), а также президентским грантом РФ НШ-1007.2003.01.