Расчет радиально-симметричных преломляющих поверхностей с учетом френелевских потерь

Расчет зеркал и преломляющих оптических поверхностей для фокусировки в заданную область является актуальной задачей светотехники [1,2]. В общем случае даже при точечном источнике света расчет оптической преломляющей поверхности или зеркала сводится к решению нелинейного дифференциального уравнения в частных производных типа уравнения Монже-Ампера [3,4]. Решение данной задачи является крайне сложным. Аналитические решения известны только для частных случаев радиальной или цилиндрической симметрии при точечном (компактном) источнике излучения [5-8].

В [5-7] рассмотрен расчет зеркала для формирования заданной диаграммы направленности и фокусировки в круг, для профиля зеркала получено аналитическое выражение. Обобщение полученного аналитического решения на случай преломляющего оптического элемента не представляет сложности. При расчете систем подсветки с размером освещаемой области значительно большим, чем толщина системы, возникает необходимость учета френелевских потерь. В данной работе рассмотрен расчет радиально-симметричных преломляющих оптических элементов для фокусировки в круг с заданной освещенностью с учетом френелевских потерь. При точечном (компактном) источнике задача сводится к решению системы обыкновенных дифференциальных уравнений, разрешенных относительно производной. По мнению авторов, полученные уравнения ранее не были опубликованы. На расчетных примерах показана эффективность данного подхода при расчете оптических элементов с размером области фокусировки на порядок большим толщины системы.

1. Расчет преломляющей поверхности

Геометрия задачи показана на рис. 1. Требуется рассчитать профиль r ( ф ) радиально-симметричного преломляющего оптического элемента из условия фокусировки в круг на плоскости z = f с заданным распределением освещенности E ( р ) . Точечный (компактный) источник света имеет интенсивность I 0 ( ф ) и находится в начале координат. Показатель преломления материала оптического элемента равен n ₁ , показатель преломления окружающей среды – n ₂ .

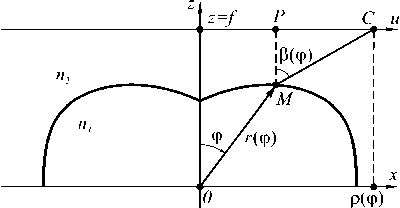
Рис. 1. Геометрия задачи

Направление луча от источника задается углом ф относительно оптической оси Oz . Пусть функ

ция в ( ф ) определяет угол между преломленным

лучом и оптической осью. При заданной функции в ( ф ) радиус-вектор r ( ф ) может быть найден из

следующего дифференциального уравнения:

dr ( ф ) d ф

- r (ф)

sin ( ф + в ( ф ) )

П 1 / n 2 - cos ( ф+в ( ф ) )

Уравнение (1) несложно получить из закона Снеллиуса. Аналогичный результат для профиля зеркала представлен в работах [5-7]. Уравнение (1) переходит в уравнение зеркала при n 1 / n ₂ = - 1. Пусть радиус точки пересечения луча с выходной плоскостью обозначается за р ( ф ) . В таком случае

функция в ( ф ) выражается из прямоугольного тре-

угольника MPC на рис. 1:

в ( ф ) = arctg

' р ( ф ) ^- r ( ф ) sin ( ф ) ' , f - r ( ф ) cos ( ф ) ,

Функция р ( ф ) определяется из условия форми-

рования требуемой освещенности E ₀ ( р ) в плоскости

z = f . Согласно закону сохранения светового потока

1 0 ( ф ) T ( ф , r ( ф ) ) d Q = E ( р ( ф ) ) d S ,              (3)

где d Q = 2 п sin ( ф ) d ф - дифференциал телесного угла, d S = 2 пр ( ф ) d р ( ф ) - дифференциал площади, р ( ф ) - координата пересечения луча с выходной плоскостью, T ( ф , r ( ф ) ) - коэффициент пропуска-

ния Френеля для неполяризованного света. Согласно выражению (3),

d p ² ( ф ) _ 2 1 ( ф ) T ( ф , r ( ф ) ) sin ( ф ) d V              E о ( р ( ф ) )

T ( ф , ^r ( ф ) ) ^_

n 2 cos ( 6 1 )	2 n 1 cos ( 6 i )
n 1 cos ( 6 i )	n 1 cos ( 6 i ) + n 2 cos ( 6 1 )

.

Коэффициент пропускания Френеля T ( ф , r ( ф ) ) для неполяризованного света равен среднему арифметическому коэффициентов пропускания для базовых поляризаций (случаи, когда вектор электрического поля перпендикулярен или параллелен плоскости падения) и зависит от углов падения 6 i ( ф ) и преломления 6 t ( ф ) луча [9]:

T ( ф , г ( ф ) ) ^_ ( T ( ф , г ( ф ) ) + ^т _±( ф , г ( ф ) ) ) /2, (5)

Величины cos ( 6 i ) и cos ( 6 t ) в (6)-(7) несложно получить в виде

cos (6 i (r (ф)))_ r (ф)

cos(61 (r (ф)))_ J1 -nrsin(6i (r (ф))) .

т±(ф,r (ф))_

n 2 cos ( ⁶ t ) n 1 cos ( 6 i )

^{d r} ( ф ) d ф

■

аф)

_ а ф

,

2 n 1 cos ( 6 i )

n ₂ cos ( 6 i ) + n 1 cos ( 6 t )

sin ф + arcrtg

-r(ф)------- n1 /n 2 -

V

г

Таким образом, с уч етом выражений (1), (2) и (4), система дифференциальных уравнений для расчета преломляющей поверхности r ( ф ) запишется в виде:

t (ф) - r (ф) sin (ф)

f - r ( ф ) cos ( ф )

V__________________22

cos ф + arcrtg

V

t (ф)- г (ф) sin (ф)

f - r ( ф ) cos ( ф )

^{V                      2} 2

I ( ф ) sin ( ф ) T ( ф , r ( ф ))/ E ( ^t ) , t ( ф ) _р ² ( ф ) ,

,

где коэффициент пропускания Френеля T ( ф , r ( ф ) ) определяется выражениями (5)–(7). В системе уравнений использована новая функция t ( ф ) _р ² ( ф ) . Она позволяет избежать особенности в уравнении (4) (деление на ноль в точке р ( 0 ) _ 0).

Система (9) содержит дифференциальные уравнения, разрешенные относительно производной, поэтому для ее интегрирования можно применять стандартные методы, например, метод Рунге-Кутта. При коэффициенте пропускания Френеля T (ф, r (ф)) = 1 система уравнений (9) распадается на два независимых дифференциальных уравнения для расчета профиля преломляющей поверхности без учета френелевских потерь. При T (ф, r (ф)) = 1 и n1 / n2 _ -1 получаются уравнения, используемые при расчете зеркал и приведенные в работах [5–7].

• 2.    Примеры расчета

Был рассчитан оптический элемент для фокусировки в круг диаметром 90 мм с постоянной освещенностью, расположенный в плоскости z _ 10 мм . Расчет проводился для ламбертовского источника с интенсивностью I ( ф ) _ cos ( ф ) , фе [ 0, п /2 ) при показателе преломления n _ 1,56 (полиметилметакрилат). Для интегрирования системы (9) использовался метод Рунге-Кутта 5-ого порядка (начальные условия: высота профиля r ( 0 ) _ 5 мм, р ( 0 ) _ 0 мм). Рассчитанный профиль оптического элемента и характерные размеры показаны на рис. 2.

Рис. 2. Профиль оптического элемента и область фокусировки с соблюдением пропорций

Расчетное распределение освещенности в плоскости фокусировки приведено на рис. 3. Расчет освещенности проводился с помощью коммерческой программы по светотехнике TracePro [10]. Распре- деление на рис. 3 близко к равномерному, средне квадратичное отклонение распределения освещен ности от постоянного значения составляет 8,2% Флуктуации освещенности связаны как с погреш ностями лучевого расчета, так и с тем фактом, что система уравнений (9) не учитывает вторичных отражений внутри линзы. Энергетическая эффективность фокусировки, определяемая как доля излученного светового потока, попавшая в круг, составляет 69% .

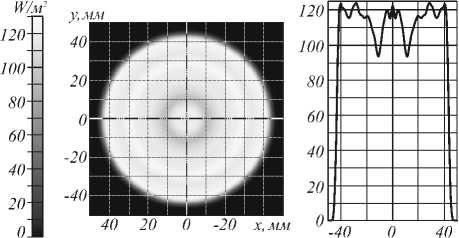
Irradiance Min:5.3959e-015 Whn\ Max: 124.35 W7m, Ave:69,69 W/nr

RMS:55.629, Total Flux:0.6969 W 9971 Incident Rays

Рис. 3. Распределение освещенности от оптического элемента, рассчитанного с учетом френелевских потерь

Для сравнения на рис. 4 показан результат расчета освещенности в выходной плоскости для оптического элемента, рассчитанного без учета френелевских потерь. Распределение на рис. 4 существенно неравномерное.

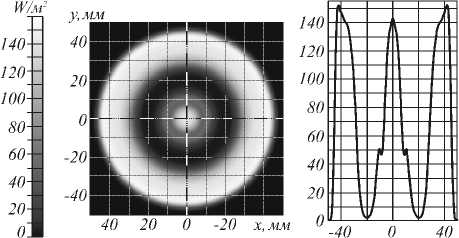
Irradiance Min:3.87Ie-013 И7т\ Max:152.32 W/nf, Ave:59,213 W/in

RMS:61.039, Total Flux:0.59213 IF 8542 Incident Rays

Рис. 4. Распределение освещенности от оптического элемента, рассчитанного без учета френелевских потерь

Темное кольцо обусловлено наличием на преломляющей поверхности области, для которой угол падения (угол между падающим лучом и нормалью к поверхности) близок к углу полного внутреннего отражения. На рис. 5 показаны зависимости угла падения и коэффициента пропускания Френеля от угла ф. Из графиков видно, что для значений фе (10°;35°) угол падения луча близок к углу полного внутреннего отражения (39,868° ) и френелевские потери составляют 75% и более. Приведенный пример демонстрирует важность учета френелевских потерь.

Заключение

Получены формулы расчета радиально-симметричных оптических элементов для фокусировки в круглую область на плоскости с учетом френелевских потерь.

Приведенные расчетные примеры показывают возможность формирования равномерной освещенности в области фокусировки при толщине системы, на порядок меньшей размера области фокусировки. Показана необходимость учета френелевских потерь при расчете оптических элементов с такими пара- метрами.

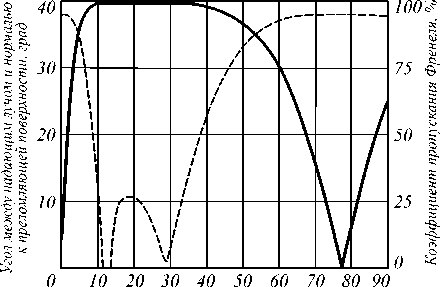
Угол ф. град

Рис. 5. Зависимости угла падения луча на преломляющую поверхность (сплошная линия, левая ось ординат) и коэффициента пропускания Френеля (прерывистая линия, правая ось ординат) от угла ф

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» ("BHRE", грант CRDF RUX0-014-SA-06), «Фонда содействия отечественной науке», грантов РФФИ № 07-07-97601-р_офи, 07-01-96602-р_поволжье_а, 08-07-99005-р_офи и Президента РФ № НШ-3086.2008.9.