Расчет размерных цепей со звеньями-эксцентриситетами

Предлагается методика вероятностного расчета технологических и сборочных размерных цепей, содержащих звенья-эксцентриситеты, в качестве математических моделей которых приняты случайные векторы, имеющие круговое или сферическое нормальное распределение. Векторная размерная цепь приводится к линейной размерной цепи, в которую в качестве составляющего звена входит модуль вектора результирующего эксцентриситета. Приведены алгоритмы вычисления математического ожидания и дисперсии этого звена для различных условий обработки и сборки.

В состав многих конструкторских и технологических размерных цепей входят звенья, с помощью которых моделируются параметры, характеризующие погрешности взаимного положения поверхностей, имеющих центр или ось симметрии, например, отклонение от концентричности наружной и внутренней сфер, отклонение от соосности осесимметричных поверхностей, отклонение центра сферы от оси кругового конуса и т.п. В дальнейшем эти звенья будем называть звеньями-эксцентриситетами.

Эксцентриситет характеризуется величиной и направлением, т.е. является вектором (трех-или двухмерным), что должно учитываться при разработке инженерных методик расчета размерных цепей, содержащих звенья-эксцентриситеты.

Математическое описание эксцентриситета

В качестве простейшего примера формирования эксцентриситета рассмотрим растачивание цилиндрического отверстия на координатно-расточном станке (рис. 1). Заготовка в виде прямоугольной плиты базируется по нижней и двум боковым сторонам, от которых должны быть вы- держаны размеры А ± а, В ± b до оси обрабатываемого отверстия.

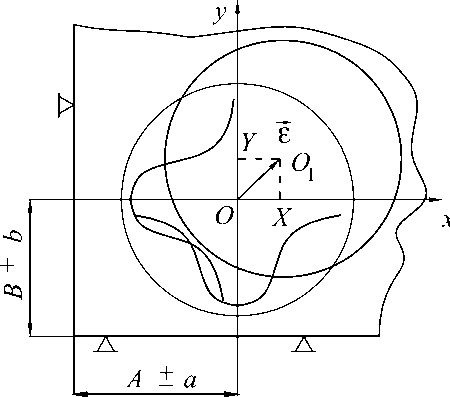
Рис. 1. Образование эксцентриситета при растачивании отверстия

Введем прямоугольную систему координат Оху , начало которой поместим в точку О , соот-

ветствующую номинальному положению оси обрабатываемого отверстия. На осях Ох и Оу будем откладывать появляющиеся отклонения действительных координат центра отверстия от их номинальных значений. Эти отклонения будем считать независимыми случайными величинами ( Х, Y ), имеющими нормальные центриро

ванные распределения:

f ( x )= e ';

f ( У ) =

y

---1= e ²° y . (1)

о y v²ⁿ

Совокупность отклонений Х и Y при каждой реализации процесса обработки определяет случайную точку О 1 - точку пересечения оси отверстия с координатной плоскостью Оху . Вектор е , проведенный в эту точку из начала координат,

является двумерным случайным вектором, проекции ( Х, Y ) которого на оси координат имеют плотности распределения, описываемые зависимостями (1).

Средние квадратичные отклонения (СКО) оx и оy характеризуют точность выдерживания координат при обработке данной заготовки на данном станке.

Если о _x = о y = о , то зависимости (1) принимают вид:

f ^{( x} ) =

1        2 о ²

e о^ 2п

f ( У ) =

y

1        2 о ²

e о^ 2п

В этом случае положение случайной точки О1 описывается круговым нормальным распреде- лением

f ^{( x} , У ) =

1       -       x ² ■ У ^{2 )}

' e ^{2 о} 2

2по2

а величину о называют радиальным СКО.

Рассмотрим одномерную случайную величину

определяющую расстояние от начала координат до случайной точки О 1. Величина £ есть модуль случайного вектора: £ = | £ |. Если вектор £ имеет круговое нормальное распределение (3), то распределение его модуля £ подчиняется закону Рэлея (рис. 2):

о?e

2 о ²

при £ >  0;

при £ <  0.

Следует отметить, что средние значения (математические ожидания МО) координат случай ной точки О 1 равны нулю (x = у = 0), а МО ее удаленности от начала координат не равно нулю и определяется соотношением

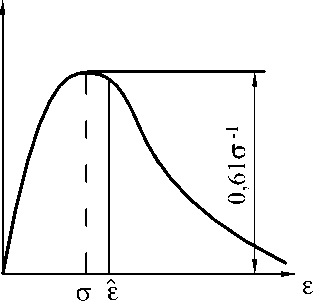
Рис. 2. Распределение Релея

А

= 1,253 о .

Значение СКО одномерной случайной величины £ о = о. 2-- = 0,6551о.           (7)

^£ V 2

Из (7) следует, что о_Е <  о . Это свидетельствует о более тесном группировании случайной величины £ вокруг своего среднего значения по сравнению с группированием случайных величин Х и Y . Максимум функции /(£) имеет место при £ = о , что не совпадает с МО. Поле рассеивания случайной величины £ , имеющей распределение (5), в инженерных расчетах обычно принимается равным 2 о_Е V7 :

ю_£ = 2 о_£V? = 5,2915 о_£ ; ю_£ = 2 о

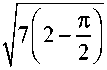
= 3,4667 о .

(8a, б)

Вероятность попадания случайной величины £ на отрезок от нуля до 3,47 о равна 99,76% [ 1 ] .

А

Соотношения (8) позволяют вычислять о_£ , о и £ по величине £ _max, регламентируемой в конструкторских и технологических документах. Согласно (4), (5) и рис. 2 £ min = 0. Поэтому

^ е ^£ max ^£ min ^£ max ^.

Из (8а) следует, что

Из (8а) и (7) находим

Из (10) и (6) находим

σ ε = ^ε ₂ ^ma ₇ ^x ≈ 0,189 ε max .

σ= ^σε = ^{ε max} = 0,288 ε max .

J 2 -П 2P ^f 2 -^П1

V 2    \ V 2 )

ε max

ε=             ≈ ,     ε _max .

Изложенные условия формирования эксцентриситета справедливы для большинства других случаев обработки деталей. Поэтому при расчете плоских векторных размерных цепей в качестве математической модели эксцентриситета в данной работе принят случайный вектор £ , имеющий круговое нормальное распределение (3). В алгебраических уравнениях линейных размерных цепей, к которым будут приводиться векторные цепи, используется математическая модель эксцентриситета в виде одномерной случайной величины ε , описываемой соотношениями (4)–(11). Эти соотношения характеризуют только расстояние от принятого начала координат до случайной точки, расположенной на конце случайного вектора ^£.

При расчете пространственных векторных размерных цепей математической моделью эксцентриситета является трехмерный вектор р со сферическим нормальным распределением

f ( x , y , z )

- ¹ ( x ² + y ² + z ²)

¹           2 σ ²

(2 π )^3/2 σ ^{3 e}

Расстояние от начала координат до случайной точки (модуль вектора р) определяется ра- венством

ρ=+ X ² + Y ² + Z ².

Плотность распределения одномерной случайной величины ρ подчиняется закону Максвел- ла [1]:

f ( Р ) = ^

^ρ σ 3 ^e

ρ ² 2 σ ²

при ρ≥ 0;

0 при р <  0.

МО и СКО случайной величины ρ :

ρ=2σ 2 ≈1,596σ;(15)

π

σρ =σ3-8 ≈0,6734σ.(16)

ρ π

Величина поля рассеивания ρ с вероятностью 99,68 % может быть принята равной

ωρ =3,7σ.(17)

В зависимости от вида уравнений размерных цепей в них может осуществляться как векторное суммирование звеньев-эксцентриситетов, так и алгебраическое суммирование их модулей.

При векторном суммировании эксцентриситетов используются правила суммирования случайных векторов [ 2 ] . Для простоты проиллюстрируем их на примере суммирования двух независимых случайных двухмерных векторов £ 1 и е ₂ , имеющих круговые нормальные распределения (3) с радиальными СКО о 1 и о ₂ . В этом случае вектор ^£ = £ 1 + £ 2 будет иметь также круговое нормальное распределение с радиальным СКО σ= σ ₁ ² +σ ²₂.

Величины σ ₁ и σ ₂ определяются соотношением (10). Распределение одномерной случайной величины £ = | £ | будет подчиняться закону Рэлея (5), а ее МО и СКО определяются соотношениями (6) и (7):

ε= 1,253 σ= 1,253 σ ₁ ² +σ ²₂; σ_ε = 0,6551 σ= 0,6551 σ ₁ ² +σ ²₂. (18a, б)

Векторную разность £ 2 - 1 = £ 2 - ^£ 1 можно представить суммой векторов ^£_{2 - 1} = £ 2 + ( - ^£ 1 ) . Вектор ( - ^£ 1 ) имеет также круговое нормальное распределение с радиальным СКО о 1 . Поэтому числовые характеристики распределения случайной величины £ 2 - 1 = | £ 2 - 1 | будут также определяться соотношениями (18).

При суммировании модулей векторов ^£ 1 и ^£ 2 следует использовать правила суммирования одномерных случайных величин. Поскольку принято, что модули ε ₁ и ε ₂ имеют распределение Рэлея с параметрами σ ₁ и σ ₂ , то

ε ^∧ _i = 1,253 σ _i ; σ_{ε i} = 0,6551 σ _i ; i = 1;2. (19a, б)

Тогда случайная величина ε′ =ε ₁ +ε ₂ имеет следующие числовые характеристики распределения

∧∧ ∧

ε′=ε ₁ +ε ₂ = 1,253( σ ₁ +σ ₂); σ′_ε = 0,6551 σ ₁ ² +σ ²₂.                (20a, б)

Случайная величина ε′′ =ε ₂ -ε ₁ (разность модулей) имеет характеристики распределения

∧∧ ∧

ε′′=ε ₂ -ε ₁ = 1,253( σ ₂ -σ ₁); σ′_ε′ =

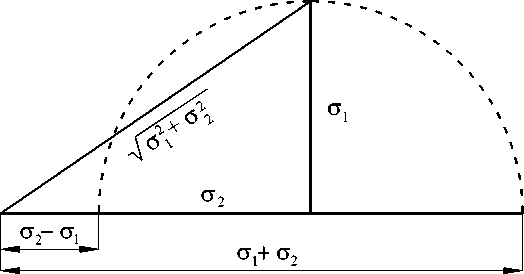
Рис. 3. Сопоставление МО модуля векторной суммы с МО суммы и разности модулей двух случайных векторов

0,6551 σ ₁ ² +σ ²₂. (21a, б)

Из сопоставления (18), (20), (21) следует, что СКО модуля векторной суммы (разности), суммы и разности модулей векторов £ 1 и £ 2 равны между собой ( σ_ε=σ′_ε=σ′_ε′ ), однако МО указанных случайных величин различны. Для наглядного их сопоставления построим прямоугольный треугольник с катетами σ ₁ и σ ₂ (рис. 3). Тогда МО модуля векторной суммы (разности) будет пропорционально гипотенузе этого треугольника, МО суммы модулей пропорционально сумме катетов

( σ ₁ +σ ₂), а МО разности модулей – разности катетов. Последняя может быть равна нулю, в то время как МО модуля векторной разности двух независимых ненулевых случайных векторов всегда отлично от нуля.

Технологические размерные цепи со звеньями-эксцентриситетами

Рассмотрим обработку на токарном станке (рис. 4). Заготовка цилиндрической формы с номинальным радиусом R базируется в трехкулачковом самоцентрирующем патроне. В результате обработки образуется новая цилиндрическая поверхность с номинальным радиусом r . В дальнейшем для краткости цилиндрические поверхности в тексте будем называть теми же буквами, что и их радиусы.

В результате действия нескольких случайных факторов между осями цилиндрических поверхностей R и r появляется эксцентриситет величиной ε .

Выберем на обработанной поверхности r произвольную точку А . Удаляемый в этой точке припуск, измеряемый по нормали к обработанной поверхности, обозначим Z . Уравнение векторной размерной цепи для припуска имеет вид

Z = Т -£- r .                                  (22)

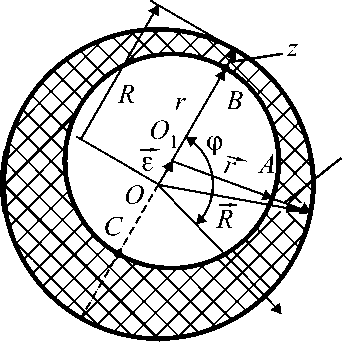
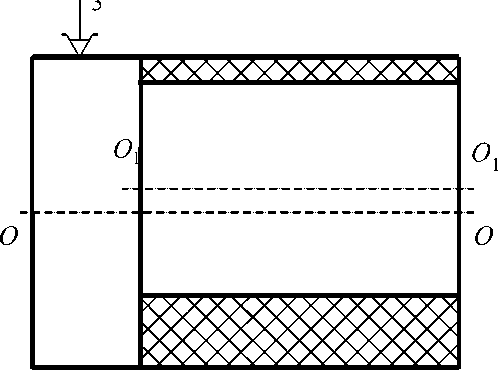
Рис. 4. Удаляемый припуск при наличии эксцентриситета

Из этого уравнения необходимо определить радиус заготовки R при известных значениях r , e , Z min . Величина Z min должна обеспечивать удаление следов предшествующей обработки и дефектного поверхностного слоя (при его наличии) и предварительно определяется расчетным путем [3]. При растачивании отверстия с радиусом R определяемой величиной в цепи (22) является r – радиус поверхности, полученной на предшествующей операции.

В соответствии с принятой математической моделью считаем, что случайный вектор е имеет круговое нормальное распределение (3). Угол ф (см. рис. 4), определяющий направление этого вектора в полярной системе координат, связанной с заготовкой, имеет распределение по закону равной вероятности в пределах от 0 до 2 п [ 4 ] .

Если пренебречь погрешностями формы цилиндрических поверхностей R и r, то при каждой реализации процесса фактическое направление вектора е однозначно определяет направление, в котором удаляемый припуск имеет наименьшее значение. Именно для этого направления и должна рассчитываться размерная цепь (22). Если погрешностями формы пренебрегать нецелесообразно, то их величину следует включить в расчетное значение Zmin в качестве дополнитель- ного слагаемого.

Для указанного направления векторное уравнение (22) вырождается в алгебраическое

поскольку все векторы, входящие в уравнение (22), становятся коллинеарными.

При расчете линейной размерной цепи (23) методом «max–min» [3] имеем

Z min = R m in ^e max r max •

Из уравнения (24) находим R _min . Максимальное значение операционного размера

D _max = 2 R m _ax находим, прибавляя к 2 R min экономически обоснованный допуск T_D :

D max = 2 R max = 2 R min + T d .                             (25)

Таким образом, получаем предельно допустимые значения операционного размера D _min = 2 R mjn и D _max = 2 R m _ax для предшествующей операции.

При расчете линейной размерной цепи (23) вероятностным методом слагаемые в правой части (23) рассматриваем как одномерные случайные величины. Исходным значением Z для определения R по-прежнему принимаем величину Z _min . Вначале запишем выражение для МО (среднего значения) Z :

A AAA

Z = R -e- r .                                   (26)

A

Величину e находим из соотношения (11). Среднее значение припуска как замыкающего звена размерной цепи (23) определяем по формуле

A

Z = Z min + 3 а _z ,                                     (27)

считая, что замыкающее звено имеет нормальное распределение, несмотря на то, что, по крайней мере, одно составляющее звено ( ε ) имеет распределение, отличное от нормального. Обоснование этого можно найти в работе [2].

Величину σ _z , входящую в выражение (27), находим как СКО суммы случайных величин:

Значение σε находим из выражения (9), а величины σR и σr – как одну шестую часть допус- ков на соответствующие радиусы:

T R

T D 12^;

σ _r

т

r

T d 12^.

Найдя величину Z из выражений (27)–(29), (9), (11), подставим это значение в уравнение

∧

(26) и найдем значение R . Предельные значения операционного размера D = 2R находим из соотношений

∧∧∧

D max,min = 2 R max,min = 2( R ± ¹ ₂ T R ) = 2 R ± T R = 2 R ± ¹ ₂ T D .               (30)

21            8021            8011

ε 1

R

r

ε2

Рис. 5. Фрагмент размерной схемы технологического процесса

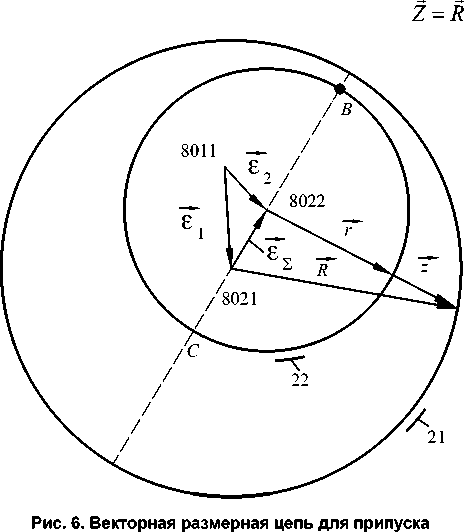
Векторная размерная цепь, показанная на рис. 6, имеет уравнение

В более общем случае эксцентриситет между обработанной и обрабатываемой поверхностями, определяющий неравномерность удаляемого припуска, есть векторная разность эксцентриситетов, определяющих положение осей указанных поверхностей. Допустим, что некоторая цилиндрическая поверхность вала обрабатывалась вначале на токарном станке, а затем на круглошлифовальном. Базирование вала на этих операциях осуществлялась по центровым отверстиям. Фрагмент размерной схемы технологического процесса [3], соответствующий указанным операциям, приведен на рис. 5. Точка 8011 соответствует общей оси центровых отверстий, точка 8021 соответствует оси поверхности 21, полученной на токарной операции, а точка 8022 – оси поверхности 22, полученной шлифованием.

►         ►

где Z - замыкающее звено-припуск; £ 1 , ^-₂ - векторы эксцентриситетов поверхностей 21 и 22 относительно общей оси центровых отверстий.

При расчете цепи (31) методом «max-min» принимаем, что направление вектора £1, проти воположно направлению вектора е2 (рис. 7). В этом случае векторное уравнение (31) вырожда- ется в алгебраическое

Z = R -ε ₁ -ε ₂ - r .

Самое неблагоприятное сочетание значений звеньев цепи (32) дает

^Z min ^{= R} min ^- ε 1max ^- ε 2max ^- r max

При известных значениях Z ,ε,ε,r из уравнения (33) можно найти R , а из min 1max 2max max                                         min уравнения (25) – Rmax .

Однако сочетание направлений и модулей случайных векторов, соответствующих рис. 7 и соотношению (33), весьма маловероятно, поэтому основным методом расчета многозвенных размерных цепей вида (31) должен быть вероятностный метод. Введем обозначение

£ _х = ^£ 2 ^- £_Р                                         ⁽³⁴⁾

Вектор ε_Σ есть вектор эксцентриситета поверхности r относительно оси поверхности R .

Подставим (34) в (31):

ε Σ - r .                                           (35)

Для того чтобы замена двух звеньев £ 1 и £ 2 в цепи (31) одним звеном £ _s была корректной, вероятностные характеристики звена £_s должны быть такими же, как и у векторной разности исходных звеньев. Поэтому числовые характеристики вектора £ _s находим как характеристики распределения суммы случайных векторов £ 2 и (- £ 1 ), имеющих круговые нормальные распределения с радиальными СКО σ ₁ и σ ₂ .

В этом случае вектор £ _s будет иметь также круговое нормальное распределение с радиальным СКО

n

σ= ∑ σ ² _j .            (36)

j = 1

В рассматриваемом случае n = 2. Величины σ j определяются на основе регламентиро- ванных в технологической документации значений ε jmax в соответствии с соотношением (10):

σ j ≈ 0,288 ε j max .

Модуль вектора £ _s (как одномерная случайная величина) имеет распределение Рэлея (5) с

МО и СКО, определяемыми соотношениями (6) и (7): ^∧ ε_Σ ≈ 1,253 σ , σ_ε∑ ≈ 0,6551 σ .

Направление случайного вектора £ _s при каждой реализации процесса определяет наиболее «опасную» точку В (см. рис. 6), в которой величина удаляемого припуска наименьшая. Векторная размерная цепь (35) для указанной точки вырождается в линейную

r

z

ε 1      ε 2

R

Рис. 7. Линейная размерная цепь для припуска при расчете методом «max–min»

Расчет линейной цепи (40) вероятностным методом производится по алгоритму, описанному для цепи (23). Отличие состоит лишь в вычислении МО и СКО звеньев ε и ε_Σ . Для звена ε , входящего в цепь (23), эти значения определяются непосредственно из соотношений (11) и (9), а для звена ε_Σ , входящего в цепь (40), – по формулам (36)–(39) через регламентируемые значения ε _{j max} .

В предыдущем примере (см. рис. 6) поверхности R и r обрабатывались от единой технологической базы. В более общем случае они могут быть обработаны от разных баз. На рис. 8 показано, что ось поверхности R (точка O R ) связана эксцентриситетом £ 3 с базовой осью, соответствующей точке O 1 , а ось поверхности r (точка O r ) связана эксцентриситетом £ 4 с базовой осью O 2 . Оси O 1 и O 2 , в свою очередь, связаны эксцентриситетами £ 1 и £ 2 с общей базовой осью, соответствующей точке О . После выявления замкнутого контура OO ₁ O_RA ′ AO_rO ₂ можно составить векторное уравнение размерной цепи для замыкающего звена – припуска Z :

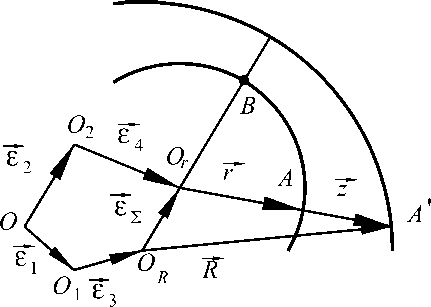
Рис. 8. Формирование многозвенной векторной размерной цепи для припуска при смене технологических баз

Z = £ 1 + £ 3 + R - £ 2 — £ 4 - r .      (41)

Как и в предыдущем случае замкнем контур эксцентриситетов звеном £ _s :

r ^ = £ 2 + £ 4 — £ 1 — £ 3 •           (42)

Подставляя (42) в (41), приходим к уравнению (35), соответствующему на рис. 8 замкнутому контуру O_RA ′ AO_r , и, в конечном итоге, к уравнению (40) линейной цепи. Отличие от предыдущего примера состоит лишь в том, что вектор результирующего эксцентриситета £ _s содержит большее число слагаемых. Поэтому при вычислении радиального СКО вектора £ _s по формуле (36) нужно принять n = 4.

Сборочные размерные цепи со звеньями-эксцентриситетами

Рассмотрим сопряжение крышки 1 с корпусом 2 (рис. 9). Крышка может устанавливаться только в одном угловом положении, определяемом штифтом 3, входящим в отверстие крышки. Одним из условий собираемости узла является наличие радиального зазора ∆= R ₂ - r ₂ между нецентрирующими цилиндрическими поверхностями корпуса и крышки.

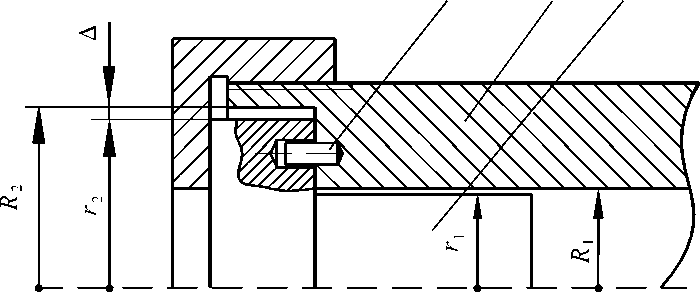
Рис. 9. Сборка при фиксированном угловом положении соединяемых деталей

Вначале рассмотрим такое взаимное положение крышки и корпуса, при котором их центрирующие цилиндрические поверхности r ₁ и R ₁ строго соосны. Положение их общей оси на рис. 10 соответствует точке О. Векторная размерная цепь, определяющая величину зазора ∆ при соосном положении центрирующих поверхностей, имеет вид

А = R 2 + E - e - r ₂, (43) где E - эксцентриситет поверхностей R ₂ и R 1 корпуса; e - эксцентриситет поверхностей r ₂ и r 1 крышки.

Вектор результирующего эксцентриситета £

- e - E , (44) определяет направление векторов R 2 и r ₂, в котором радиальный зазор А имеет наименьшее значение при данной реализации процесса. Как и в случае наименьшего припуска составим для этого направления линейную размерную цепь

∆= R ₂ -ε_Σ - r ₂. (45)

За счет радиального смещения крышки на величину ( R ₁ - r ₁) зазор ∆ может быть увеличен. Поэтому уравнение (45) принимает следующий вид

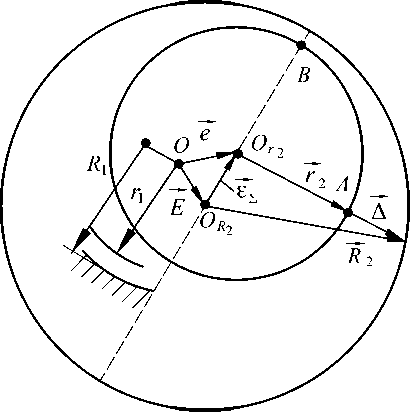
Рис. 10. Векторная размерная цепь для расчета зазора

∧

∆= ( R 1 - r 1 ) + ( R 2 - r 2 ) -ε Σ . (46)

Уравнение (46) отличается от уравнения (40) технологической размерной цепи наличием не одной, а двух разностей радиусов. Однако это отличие не является принципиальным, поэтому алгоритмы расчета цепей (40) и (46) совпадают. Вначале по формулам (36)–(39) на основе регламентированных значений ε _1max = E _max и ε _2max = e _maxнаходим

∧

МО εΣ и СКО σε∑ составляющего звена εΣ . Далее находится дисперсия σ2∆ замыкающего звена суммированием дисперсий составляющих звеньев цепи (46), а затем СКО σ∆ . Расчет ведется по формулам, аналогичным (28), (29). Затем по формуле, аналогичной (27), находится МО замыкающего звена (∆ ). После этого по формуле, аналогичной (26), находится ∧

МО искомого звена, например r ₂ , и по формуле (30) – его допустимые предельные значения.

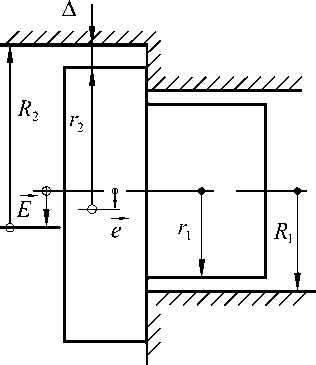
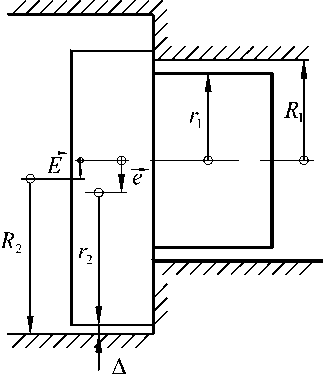
Если в узле, показанном на рис. 9, убрать штифт 3 и допустить возможность подбора углового положения крышки относительно корпуса, то эксцентриситеты крышки e и корпуса Е могут быть частично взаимно скомпенсированы. Рассмотрим сечение узла той радиальной плоскостью, в которой расположен вектор эксцентриситета корпуса E (рис. 11). Вначале, как и ранее, принимаем, что центрирующие поверхности R 1 и r 1 расположены строго соосно. В зависимости от соотношения эксцентриситетов Е и e возможны два случая.

б)

Рис. 11. Расчетная схема сопряжения при подборе углового положения соединяемых деталей

а)

Если Е >  e , то наименьший зазор будет в направлении, противоположном направлению вектора E (рис. 11а). Этот зазор можно увеличить разворотом крышки в такое угловое положение, при котором направление вектора ее эксцентриситета е будет совпадать с направлением вектора E . Тогда уравнение для наименьшего зазора принимает вид

∆= ( R 2 - r 2 ) - ( E - e ).                                 (47)

Если Е < e, то наименьший зазор будет в направлении, совпадающем с направлением векто- ра е. Его можно также увеличить за счет одинакового направления векторов E и е (рис. 11 б). Уравнение для наименьшего зазора имеет вид

∆=(R2-r2)-(e-E).(48)

Уравнения (47) и (48) можно объединить:

∆=(R2-r2)-E-e.(49)

Зазор ∆ можно дополнительно увеличить за счет радиального смещения крышки на величину ( R ₁ - r ₁). Окончательно получим

∆=(R2-r2)+(R1-r1)-E-e.(50)

При расчете размерной цепи (50) методом «max–min» необходимо найти неизвестный размер, например r 2 , обеспечивающий величину зазора ∆ не менее заданной величины ∆ min при самых неблагоприятных сочетаниях размеров соединения и абсолютной максимальной величине результирующего эксцентриситета E - e =ε . Величина ε принимает максимальное значение, если один из эксцентриситетов принимает максимальное значение, а второй – минимальное, т.е. равен нулю. С учетом того, что в общем случае E _max ≠ e _max , запишем

E - e =ε   = max { E , e } .

_max max          max max

При заданном значении ∆ min величину r 2 max находим из уравнения min 2min r 2 max    1min r 1max ε max ^.

Величину r 2 min находим, вычитая из найденного r 2 max допуск на этот размер.

При проверочном расчете размерной цепи (50) вероятностным методом вначале находим среднее значение (МО) зазора:

∧∧∧∧∧∧∧

∆=R2-r2+R1-r1-|E-e|.(53)

При расчете СКО σ_∆ используем правило суммирования дисперсий:

σ∆ =σ2R2+σr22+σ2R1+σr21+σ2E+σe2.(54)

∧ ∧

Величины E , e , σ _E , σ _e , входящие в уравнения (53), (54), находятся по формулам (11) и (9).

Предельные значения зазора ∆

∆max,min =∆∧±3σ∆.(55)

При проектном расчете цепи (50) с целью нахождения неизвестного размера, например r 2 , задается минимально допустимое значение радиального зазора ∆ _min . В этом случае рассчитанное

∧ по формуле (54) значение σ∆ используется для определения МО ∆ :

∆ ^∧ =∆ min + 3 σ ∆ .                                  (56)

∧

Это значение подставляется в уравнение (53), из которого находится r2 . Предельные значе- ния этого размера

∧ ₁ ∧ ₁

r2max,min =r2±2Tr2=r2±4Td2, где Td 2 – заданный допуск на диаметр d2= 2r2

Рассмотрим узел с резьбовым креплением крышки 1 в корпусе 2, показанный на рис. 12. Центрирование крышки относительно корпуса осуществляется с помощью гладкого цилиндриче- ского сопряжения ∅60   . Крепление – с помощью резьбы M64×2 -

.

g 7                                        5 g

Условием собираемости является наличие гарантированного радиального зазора, например ∆ _min ≥ 40 мкм , между резьбовыми поверхностями корпуса и крышки при наличии эксцентриситетов этих поверхностей относительно гладких цилиндрических как у корпуса ( Е ), так и у крыш-

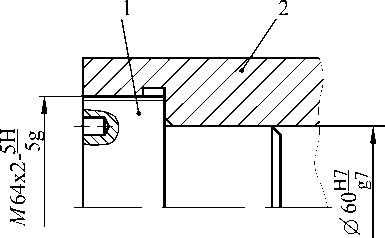
Рис. 12. Сопряжение по гладкой и резьбовой поверхностям

ки (e). Поскольку в процессе сборки крышка поворачивается относительно корпуса, то величина зазора А будет наименьшей при таком угловом положении крышки, при котором направление вектора ее эксцентриситета e будет противоположным по отношению к направлению вектора эксцентриситета E корпуса. Такое взаимное положение указанных векторов обязательно будет иметь место при каждой реализации процесса сборки. Поэтому расчетная схема (рис. 13) составляется именно для этого взаимного положения крышки и корпуса. Сопряжение по резьбовым поверхностям на цилиндрическим поверхностям с (D2) и крышки (d2).

Уравнение размерной цепи

схеме условно показано как сопряжение по гладким диаметрами, равными средним диаметрам резьбы у корпуса

^А = ( R 1 ^{- r} 1 ) + ( R 2 ^{- r} 2 ) ^- ( E + e )•

Если бы условие собираемости выражалось неравенством А >  0, то из (58) следовало бы, что

⁽ R 1 ^{- r} 1 ) + ⁽ R 2 ^{- r} 2 ) >  ⁽ E + e ),

т.е. сумма радиальных зазоров (без учета эксцентриситетов) должна быть больше суммы эксцент риситетов у сопрягаемых деталей (или равна ей) при любой реализации процесса.

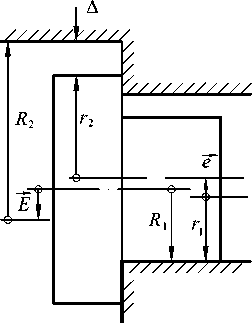
Рис. 13. Расчетная схема сопряжения по гладкой и резьбовой поверхностям

При расчете размерной цепи (58), например, с целью выбора резьбовой посадки (размера r 2 ) или проверки условия собираемости, числовые характеристики одномерных случайных величин Е и e следует рассчитывать по формулам (9) и (11). Проверим выполнение условия собираемости при конкретных размерах сопрягаемых поверхностей, указанных на рис. 12. Поля допусков средних диаметров резьб, а также диаметров цилиндрических центрирующих поверхностей показаны на рис. 14. Вначале проведем расчет методом «max–min». Из уравнения (58) следует

^А min = ⁽ R 1 ^{- r} 1 ⁾ min + ⁽ R 2 ^- ^mm ^{- (} E + e ) max • ⁽⁶⁰⁾

Назначим допуски соосности резьбовых поверхностей относительно гладких центрирующих у корпуса и крышки равными 25 мкм (в радиусном выражении), тогда ( E + e ) max = 50мкм, А min = 5 + 19 — 50 = — 26 мкм • Условие собираемости не выполнено.

При расчете вероятностным методом:

А = 2 [ ( 15 + 25 ) + ( 95 + 108 ) - 0,362 • 50 ] = 112,45 мкм;

3 о_А = 3.

/ЗОГ МОГ М90Г М40Г        .        .

, 30 + 30 + _90 + _⁰ + (0,18 9 . 25) 2 + (0,189 . 25) 2 = 63,21 мкм;

^ [12J [12J [ 12 J [ 12 J

А _min = А- 3 о_А = 112,45 - 63,21 = 49,24 мкм.

Условие собираемости выполняется ( А _{mi n} >  40 мкм).

Из приведенных примеров следует, что алгоритм расчета результирующего эксцентриситета, включаемого в линейные сборочные размерные цепи, определяются способом сборки.

Если при сборке отсутствует возможность взаимного поворота соединяемых деталей вокруг осей их центрирующих поверхностей (см. рис. 9), то взаимное угловое положение эксцентриситетов сопрягаемых поверхностей случайно, и при вероятностном расчете вначале находится векторная разность указанных случайных векторов-эксцентриситетов (см. рис. 10 и (44)), а в вырожденную линейную размерную цепь в качестве уменьшающего звена (по отношению к минимальному зазору) включается модуль этой векторной разности (см. (46)).

+190

5 H

-38

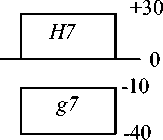
-178

5 g

Рис. 14. Схема расположения полей допусков гладких и резьбовых поверхностей

При сборке с возможностью взаимного поворота соединяемых деталей размерная цепь сразу записывается в линейном виде. В качестве уменьшающего звена в нее входит абсолютное значение разности модулей эксцентриситетов (см. (50)).

Если при сборке или при эксплуатации необходим взаимный поворот соединяемых деталей на угол ϕ ≥ 360 ° (см. рис. 12), то в линейную размерную цепь в качестве уменьшающего звена включается сумма модулей эксцентриситетов сопрягаемых поверхностей у соединяемых деталей (см. (58)).

В более сложных случаях результирующий эксцентриситет может определяться с использованием всех перечисленных выше правил. Рас-

смотрим узел, изображенный на рис. 15. При запрессовке втулки 4 в крышку 2 взаимное направ-

ление их эксцентриситетов ^—_вт и Обозначим — р + ^— _вт = е _х . Вектор оси поверхности r 3 .

—— e кр

—— ε _Σ

случайно, поэтому они суммируются векторно (рис. 16). определяет эксцентриситет поверхности R 1 относительно

R

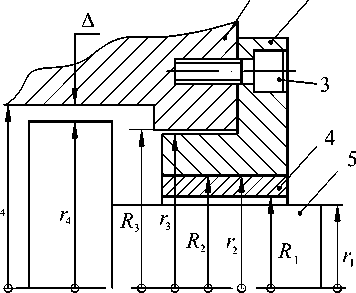
Рис. 15. Эскиз узла

— рованного эксцентриситета Eк - es . Если

При установке крышки 2 в корпус 1 она может быть повернута на угол, кратный 360 ° / n , где n - число крепежных винтов 3. При n ≥ 8 дискретностью угла поворота пренебрегаем и считаем, что условия сборки соответствуют рис. 11, т.е. векторы эксцентриситетов E к и е _х сонаправлены (см. рис. 16). Вектор E _к определяет эксцентриситет поверхности корпуса R 4 относительно оси его поверхности R 3 .

И наконец, при установке вала 5, вращающегося при эксплуатации, считаем, что вектор его эксцентриситета ев (отклонение от соосности поверхности r4 относительно оси поверхности r1) направлен про- тивоположно по отношению к вектору нескомпенси-

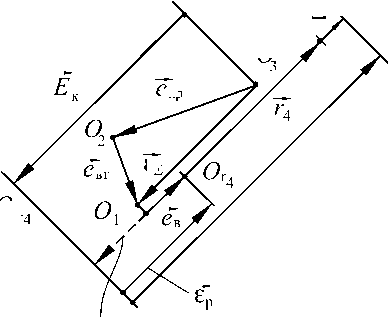
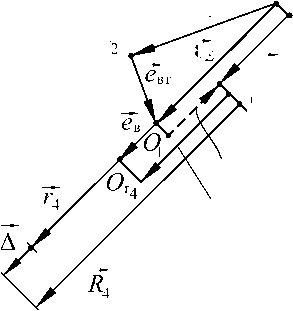
Eк > ех (рис. 16а), то вектор ев направлен противопо ложно вектору Eк, если Eк < Ev (рис. 16б), то вектор —в сонаправлен с вектором Eк. В том и другом случаях вектор ев удаляет точку Or4, расположенную на его конце, от точки OR4, расположенной на конце вектора Eк . Точки Оi (i = 1, 2, 3) соответствуют концентричному положению осей поверхностей Ri, ri. Точки OR4 и Or4 соответствуют положению осей поверхностей R4 и r4. Вектор OR4Or4 = Ер определяет результирующий эксцентриситет поверхности r4 относительно поверхности R4. С учетом принятого направления векторов модуль вектора результирующего эксцентриситета

εр =Eк-εΣ +eв.(61)

Вектор ^— р определяет направление, в котором зазор А принимает наименьшее значение при каждой реализации процесса сборки. Уравнение линейной размерной цепи для этого направления имеет вид (см. рис. 16)

∆=R4-r4-εр =R4-r4-Eк -εΣ -eв .(62)

С учетом наличия зазоров в сопряжениях

∆=(R1-r1)+(R3-r3)+(R4-r4)-|Eк -εΣ |-eв .(63)

A

О

eкр e вт

О

О ₂

E y

О

О R

R 4

Е к "  E y

e кр

О

О 3

E y

Е к ■ ^£y

EP

Е к

О R4

б)

Рис. 16. Сборочные размерные цепи для узла, изображенного на рис. 15

При применении посадки с гарантированным натягом «зазор» ( R 2 - r 2 ) <  0, поэтому принимается равным нулю.

Числовые характеристики случайной величины E_y = | е _кр + е _вт | вычисляются по формулам (36)–(39). Характеристики случайных величин E _к и e_в вычисляются по формулам (9) и (11).

В остальном алгоритм расчета размерной цепи (63) не отличается от алгоритма расчета цепи (50).

Заключение

Предложена методика двухэтапного расчета векторных размерных цепей, определяющих значение припуска ( Z) или зазора ( A ). На первом этапе производиться векторное суммирование эксцентриситетов, входящих в цепь, и определяются вероятностные характеристики модуля вектора результирующего эксцентриситета ( E р ) меньшей поверхности ( r ) относительно большей ( R ).

Технологическая векторная многозвенная размерная цепь приводиться к четырехзвенной линейной размерной цепи вида

На втором этапе производиться расчет этой размерной цепи традиционными методами.

Сборочные векторные размерные цепи приводятся к линейным цепям вида

n

A=Е(R—r) i—E р • i=1

При определении вероятностных характеристик звена E _р не все эксцентриситеты, входящие в исходную сборочную цепь суммируются векторно. Приведены правила суммирования эксцентриситетов в зависимости от способа сборки или условий функционирования сборочной единицы.