Расчет рефлекторов для формирования диаграммы направленности в виде кривой

Рассмотрен расчет рефлекторов для формирования диаграммы направленности (ДН) в виде кривой. Установлен тип лучевой структуры поля при формировании ДН в виде кривой. Расчет рефлектора для формирования ДН в виде отрезка сведен к задаче расчета цилиндрического профиля с заданной функции лучевого соответствия. Получено интегро-дифференциальное уравнение для решения обратной задачи формирования ДН в виде отрезка.

1. Расчет поверхности рефлектора

В работе [1] рассмотрен расчет зеркальных поверхностей для фокусировки в заданную кривую в пространстве. В работе [1] не рассмотрен практически важный случай формирования диаграммы направленности (ДН) в виде кривой. На взгляд авторов задача формирования ДН имеет свои особенности и ряд специфических свойств, которые не могут быть получены непосредственно из общих соотношений работы [1].

В задаче формирования ДН кривую будем считать определенной в виде

Р ⁽ ^ ) = ⁽ Р х ^{( ст} ), Р у ^{( ст} ), P z ^{( ст} ) ) Р ⁽ ^ ) = ¹ , ⁽¹⁾ где р (о) - единичный вектор направления. Таким образом, в терминах ДН кривая может интерпретироваться как линия на единичной сфере, радиус -вектор которой определяет направление отраженных лучей. Рассмотрим расчет поверхности рефлектора для формирования ДН (1) при точечном источнике с центром в точке Q . Без ограничения общности точечный источник будем считать расположенным в начале координат.

Поскольку поверхность рефлектора двумерная (т.е. зависит от двух переменных), а кривая (1) -одномерная, то поверхность рефлектора должна состоять из кривых P (£; о) на каждой из которых отраженные лучи имеют направление р (о). Параллельный пучок с направлением р (о) формируется параболоидом с уравнением

|M| - ( р ( ст ), M ) = 2f , (2) где M = ^х² + у² + z² - радиус-вектор точки поверхности параболоида с центром, f - фокус параболоида.

Для уяснения структуры кривых P (£; о) рассмотрим пересечение двух параболоидов с центром в точке Q и с направлениями осей р (о), р (о+ Д о)на две близлежащие точки кривой;

/ M - ( р (а), M ) = 2 f ( а ) , M - ( p (а + Аа), M ) = 2 f ( а + Аа ).

При Д о^ 0 уравнения (3) примут вид:

| M| -⁽ Р ( а ), м ) = 2 f ( а ),

’ f ^,M ) = - 2 dfM. ’ ( d а    J      d а

Уравнение (4) является огибающей семейства параболоидов. При этом кривые P (£; о) соответствуют пересечениям параболоидов с плоскостями, перпендикулярными касательным к кривой (1). Множество кривых P (£;о) по параметру о формирует поверхность рефлектора.

Уравнение рефлектора определим в виде

м ( ст , t ) = д ( ст , t ) + р ( ст ) • R ( ст , t ) ,                  (5)

где

^{2 f} " ^{( ст} )• P " ^{( ст} L р ^{( ст )x} P ст ^{( ст} ), а ( ст , t 1 =----- +1--------------------г • t - (6)

|p ст ( ст )           |^{р( ст )x p} ст ^{( ст} )

- радиус-вектор точки прямой, являющейся пересечением плоскостей

,Р^{( ст} ^ ’ = 0    .                       (7)

| p ст ( ст ), M ) =- 2 Ч„ст ).

Функция

„/ лq2(ст,t)-f2(ст) Rст t ) = -     2f (ст)

является длиной вдоль направления р (о) от точки прямой (6) до параболоида |м| - ( р ( ст ), M ) = 2f ( ст ) . Следует отметить, что выбор системы прямых (6) неоднозначен. Например, в качестве прямых (6) можно использовать пересечение плоскостей ( р _ст ( ст ), M ) =- 2f _ст ( ст ) с некоторой фиксированной плоскостью. Мы выбрали систему (6), поскольку она содержит в явном виде вектора бинормали Ь ( ст , t ) = р ( ст ) х р ст ( ст ) /| р ( ст ) х р ст ( ст ) и касательной т⁽ ст , t ) = р ст ⁽ ст ) /|рст ⁽ ст ) к кривой ⁽¹⁾.

Функция fо) в (6)-(8) является аналогом эйконала при фокусировке в пространственную кривую [1]. Выбор функции fо) можно проводить из условия формирования заданной интенсивности I(о)на кривой. Из-за громоздкости мы не будем приводить расчетные формулы дляfо) в общем случае. Расчет функции эквивалентной f(σ) для случая ДН в виде отрезка рассмотрен в следующем пункте.

Уравнения (9)-(11) позволяют записать уравнение поверхности рефлектора через функцию р ( с ) в

2. Расчет рефлектора для формирования ДН в виде отрезка

Задача формирования ДН в виде отрезка является наиболее практически интересным случаем. Хотя функция f (σ) определяет все характеристики рефлектора, однако, с точки зрения инженера-расчетчика, выбор функции f (σ) из условия контроля энергетических характеристик формируемого пучка и геометрических параметров рефлектора является трудной задачей. Предлагается расчет трехмерной поверхности рефлектора проводить через расчет цилиндрического профиля для фокусировки в отрезок, являющегося центральным сечением рефлектора. Это позволяет заменить выбор функции f (σ) функцией лучевого соответствия, имеющей ясный физический смысл и позволяющей контролировать геометрические параметры рефлектора.

виде

f x ^(с , t fi ^{м ( с} , у ) = у ^{( с} , t ) =

ч z(с, tL

f r(с)•sin(с)"

_y _ k- r (с )• cos(с)y

+

+

' srn pp )f 0

k cospp)) 7

,

•

y2

4/ (с)

где ( с , у ) - цилиндрические координаты. Представление поверхности рефлектора в виде (12) является удобным, поскольку функции в ( с ) и r ( с ) явно

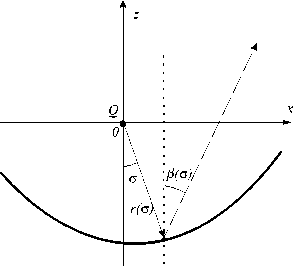
Рис. 1. Цилиндрический рефлектор для формирования ДН р^с ) •

определяют направление отраженных лучей и геометрические размеры рефлектора.

Рассмотрим расчет функции р ( с ) из условия формирования заданной интенсивности I ( р ) на отрезке. Запишем уравнение сохранения светового потока в дифференциальной форме;

dP = y2 г") Io (с, t) f М((с, t)) N(с, t)' dс у1 с) м2 ((с, t)) k М(с, t)), Нс t) v

X

x |н(с, t) dt где Io (с, t) - интенсивность точеного источника, Н(с, t)=дМ(с, t) хдМ(с, t) - дс       д t

Рассмотрим расчет цилиндрического профиля r (σ) из условия формирования заданной функции лучевого соответствия, определяющей угол отраженного луча β(σ) в зависимости от угловой координаты ff e [ ff - , с 2 ] падающего луча (Рис.1). Функция r ( с ) может быть получена из закона отражения

нормальный вектор к поверхности рефлектора, y 1 (σ), y₂ (σ) - функции определяющие размер рефлектора по оси OY. Подставляя (12) в (13), получим интегро-дифференциальное уравнение для функции β(σ);

dp

---= r dс

У 2 ^{( с} )

(с) j H ((с, t ))dt /

У 1 ^{( с} )

в виде [2]:

/1 (в)+у2 jH((с, t ))• k          У1(с)

t2

dt

4f (с)

r(с ) = ro •

^f с. I exp j tan l k ^с 0

4 - P^Vl

2 d

где

Уравнение (9) при β(σ)>0 определяет профиль эллиптического типа, когда отраженный луч пересекает ось z, а при β(σ)>0 - профиль гиперболического типа, для которого отраженный лучи не пересекают оптическую ось. Рассматривая профиль (9) как сечение трехмерного рефлектора для фокусировки в

H((с,t»= 1( } '0(с't’,     X

(r (с)+t2 /4f (с))

2 ^t

х| r(с )--I

k      4f (с)'

.

отрезок

Р(с) = (- sin(P(с)) 0, cosp^))), сНс0 ,с1]

несложно получить функцию f ( с ) в виде: f с - в ( с ) )

f (с) = r(с)• cos I2^1

В общем случае при численном решении интегро-дифференциального уравнения производные и интегралы заменяются разностными и квадратурными формулами, что сводит исходную задачу к решению системы нелинейных уравнений относительно отсчетов искомой функции. Использование формулы прямоугольников для интеграла (9) позволяет свести решение уравнения (14) к применению простейшего метода Эйлера, что является несомненным достоинством полученных формул.

Рассмотренная задача формирования отрезка может рассматриваться как эталонная задача формирования сложной ДН, состоящей из набора отрезков. Для формирования набора отрезков можно использовать сегментированную поверхность, каждый сегмент которой формирует свой отрезок. На Рис. 2 приведен рассчитанный сегментированный рефлектор для формирования ДН в виде звезды Давида. Рефлектор был рассчитан для демонстрационных целей и предназначался для фокусировки излучения от светодиода с угловой диаграммой с е [ - 40°, - 40° ] . Шесть угловых сегментов рефлектора формируют шесть отрезков с угловым размером 30⁰ , составляющих звезду Давида. Центральный сегмент создает окружность внешнюю окружность. Расчет угловых сегментов проводился по формуле (12). Центральный сегмент является поверхностью вращения с образующей, соответствующей наклонной параболе. На Рис. 3 приведено расчетное распределение интенсивности, формируемое рефлектором в дальней зоне. Расчет поля проводился с использованием 'ray-tracing алгоритмов', реализованных в рамках программного продукта ASAP_BRO.

Результаты расчетов показывают хорошее качество фокусировки и подтверждают работоспособность разработанного метода расчета.

• 3.    Заключение

В работе получено, что лучевая структура поля при формировании ДН в виде кривой (1) определяется тем свойством, что все лучи с направлением p (σ)находятся в плоскости с нормальным вектором Р Сс ( ^С ) .

Данный факт может быть использован при расчете любых типов оптических элементов для формирования ДН в виде кривой. В частности, при расчете фокусаторов лазерного излучения [3,4] указанное свойство приводит к системе слоев вида

dpx (с)    dPy(с)

X г xv / + у л---= d (с)

de de где d(σ)- некоторая функция.

a)

14.84 mm

£ £

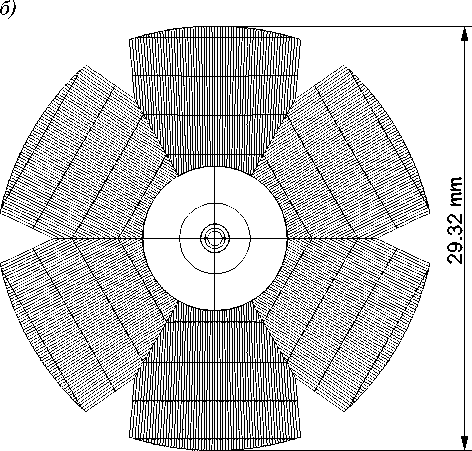
Рис. 2. Геометрия положения рефлектор – светодиод (а) и вид сверху (б) поверхности рефлектора.

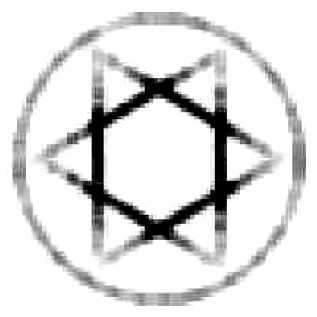
Рис. 3. Расчетная диаграмма направленности, формируемая рефлектором на рис.2.

Интересно отметить, что слои (16) являются прямыми, как и для случая фокусировки в кривую в параксиальном приближении [3,4]. Однако, вид слоев (16) не совпадает с известными уравнениями для параксиального случая [3,4].