Расчет составного градиентного оптического элемента, формирующего заданное распределение интенсивности

Впервые обратная задача в геометрической оптике неоднородных сред была поставлена и частично решена в [1, 2]. В [1] найдено аналитическое решение для двумерного волновода, периодически фокусирующего лучи, исходящие из осевой точки. В [2] по заданному двумерному семейству лучей в ГОЭ построено общее решение для показателя преломления, зависящее от некоторой произвольной функции. Однако это решение не учитывает физические ограничения.

В данной работе общее решение уточнено и обобщено для случая плоского входного фронта и фокусировки лучей в произвольной осевой точке. На основе аналитического решения рассмотрены составные ГОЭ, состоящие из отдельных зон удовлетворяющих полученному решению. Подобные ГОЭ могут быть использованы для формирования заданного распределения интенсивности в выходной плоскости.

В работе [1] найдено решение для подобного уравнения в виде:

n ( x ) =

n ₀

ch ( ^ 2 x )

При этом уравнение семейства лучей примет вид:

x ( z , v ) = — Arsh n

П .

sh — v ■ sin — z

где v – параметр, определяющий конкретный луч.

Данное решение найдено для случая, когда в точке z =0 находится источник цилиндрической волны, при этом в точках z =2 k +1, где k e N, все выходящие из источника лучи становятся параллельны, то есть фронт волны становится плоским, а в точках z =2 k все лучи вновь собираются в точке x =0 (рис. 1).

X, мм.

Z, мм.

Рис. 1. Цилиндрический фронт. Сходимость в точках z=2k, k e N

1. Аналитическое решение

Запишем уравнение луча [3] в среде с показа-

телем преломления n :

—*

d I I

I    n I = V n .

d S I d S

Полагая, x = x ( z ), y = y ( z ), d S = dx 2 ² + d У ² + dz ² -

малое расстояние вдоль луча, получим следующую

систему уравнений:

d x dn dn । ---■ d z d z d x )

| dx I2 | dy I2

1+ I I +I I

I dz ) I dz )

d y d n  d n

^^^^^^^^^^^^^^S  ^^^^^^^^^^^^^^^  ^^^^^^* ^^^^^^^^^^^^^^^f dz dz  dy

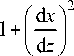
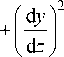
_d2 _y

+ n

_d2 _x

+ n  ₂

d z

= 0

, (2)

= 0

Рассмотрим среду с непрерывно меняющимся в направлении x показателем преломления n ( x ). Предполагая среду бесконечно протяженной вдоль оси y , приходим к:

2 d x    dn ( dx । n—уI I= 0 , dz2    dx ( dz )d или:

_d2 _x

£dn = n dxd

1 + ( /dz)

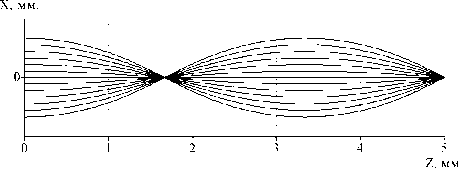
Рис. 2. Плоский фронт. Сходимость в точке z=d, d=1,65

Модифицируем это решение так, чтобы для случая плоского фронта в точке z =0 лучи сходились бы в некоторой точке z = d (рис. 2). Тогда уравнения (5 и 6) следует переписать в виде:

n ( x ) =

n ₀

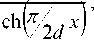
x ( z , v ) = —Arsh n

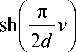
■ cos

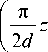
Очевидно, что при возрастании х значение n ( x ) будет быстро убывать. В результате при некотором определенном значении x мы получим значение n ( x ) < 1, что физически некорректно.

Для устранения некорректности необходимо выражение (7) дополнить условием:

D - b2 - 4 ■ a ■ c > 0.

n ( ^x ) ^ n min .

С учетом последнего условия из выражения (7) можно получить следующее неравенство:

Проведя несложные преобразования, учитывая, что величина A_k < 0, а также выбирая единственный корень из соображений направления луча, можно получить:

Y xmax

< 2d- Arch

n ₀

ⁿ L n min

x I ^{+ 1} x_k

l

= x k

^A7+

Таким образом, мы получили выражение для апертуры реального оптического элемента при заданных величинах d , n 0 и n min .

V1 - 4Ak т2 - 4|Ak |(xk 1 - xk )

+        2AJ

2. Численное решение

Для численного решения уравнения (4) перепишем его в виде:

и

⁴ A k т ^{2 +} 4 A k ^ x k ^{- 1 -} x k ) <  1.

1 +

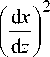
1 d n d² x n d x d z ²

Заметим, что для сходимости лучей на оси тре-dn        d2x буется, чтобы:   < 0 => —— < 0 - то есть все лучи dx        dz2

Из уравнения (18) следует, что при начальном условии x k = x k (плоский фронт волны на входе): x k <  x k . И далее следует, что при V 1 будет выполняться неравенство:

0 <  x k ⁺ 1 <  x k (20)

сходятся к оси “выпукло” (рис. 1, 2).

Зададим сетку с узлами в точках ( x , z )=( kh , 1 т ), где h = x m», т = d - шаги сетки, k = 0,N , 1 = 0,M .

NM

Следует заметить, что величину A k с учетом выражения (7) можно определить и в аналитическом виде, а именно:

л

A k ( x ) = -— th 2 d

П

2 d

x

Запишем разностную схему:

1 +

' xd

² xk

т

V          7

¹ n k ^- n k - 1

--:-- nkl      h

x k ¹ - ² x k ⁺ x k ^{+ 1}

xk = xk ,

n 0 = n ₀( kh ).

Для удобства записи переобозначим:

1 nk - nk-1 _ „ т ;    - Ak, nkl     h

3. Численное моделирование

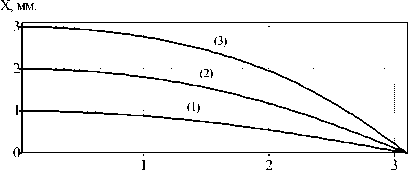
Для исследования хода лучей внутри рассматриваемой среды было разработано программное обеспечение, реализующее численное решение (18). На рис. 3 показан ход лучей с различными начальными координатами на входе (соответственно 1, 2 и 3 мм). Параметры расчета: ширина элемента x max = 3 мм, расстояние до точки схождения лучей d = 3,1 мм, минимальный и максимальный коэффициенты преломления соответственно n min = 1 и n 0 = 2,5; количество отсчетов: по вертикали – 100, по горизонтали – 1000.

Заметим, что A_k <  0 , так как n k >  n k - 1 , для

сходимости лучей на оси x =0. Тогда:

Ak ’(xk+1) - (2Akxk + 1)’ xk+1 +

+ VAkT2 + Ak(xk) + 2xk -xk 17 = 0.

Введем обозначения:

a - Ak , b - 2Akxk +1 ,

c - AkT2 + Ak(xk) + 2xk -xk 1 .

Тогда:

a ■ (xk+1) — b ’ xk+1 + c = 0 .

При этом необходимо выполнение условия:

Z, мм.

Рис. 3. Рассчитанный ход для лучей с координатами на входе: 1 мм (1); 2 мм (2); 3 мм (3).

Для экспериментального подтверждения сходимости численного решения (18) были проведены различные исследования поведения ошибки £ На рис. 4 для соответствующих лучей показаны зависимости СКО от изменения количества отсчетов по горизонтальной оси z (то есть от измельчения шага т ) при фиксированном количестве отсчетов по оси x . Данная ошибка показывает отклонение хода лучей рассчитанных по численной схеме (18) от аналитического решения (8). На рис. 5 показаны зависимости СКО при одновременном изменении количества отсчетов по осям x и z , при этом

сохраняется соотношение: χ ≡ τ / h = const. Приведенные графики демонстрируют хорошую устойчи-

вость полученного решения.

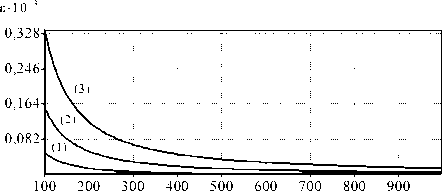
Рис. 4. Исследование зависимости ошибки от количества разбиений по оси z для лучей с координатами на входе: 1 мм (1); 2 мм (2); 3 мм (3).

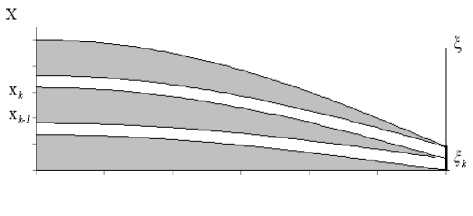
Рис. 7. Разбиение составного ГОЭ на зоны.

Число лучей N 1 - N M , где M – количество отсчетов на входе, которые должны придти в конкретный отсчет выходной плоскости (“ширина” зоны), можно итеративно определить в соответствии с заданным распределением интенсивности I_В ( ξ ) на выходе по следующим формулам:

N p

I В ( ξ p ) ≅ ∑ I 0 ( x k ), p = 1, M , N 0 = 0, (22) k = N p - 1 + 1

M

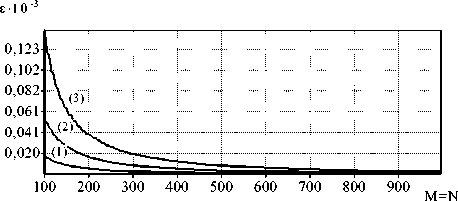
Рис. 5. Исследование зависимости ошибки от количества разбиений по осям x и z, при χ ≡ τ /h = const для лучей с координатами на входе: 1 мм (1); 2 мм (2); 3 мм (3).

Также было проведено исследование распределения интенсивности по вертикальной оси x на различных расстояния от входной плоскости z =0. На рис. 5 показаны профили интенсивности в точках z = 2,9 мм (1); z = 3,0 мм (2); z = 3,05 мм (3). Параметры расчета совпадают с параметрами предыдущих экспериментов (то есть общее число лучей во входной плоскости равно 100).

Кол-во луч ей

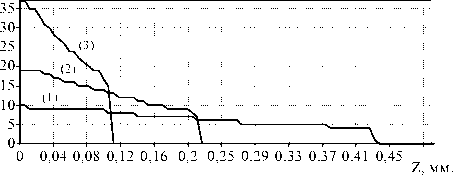
Рис. 6. Исследование профиля интенсивности в точках: z = 2,9 мм (1); 3,0 мм (2); 3,05 мм (3).

где xk , ξp – координаты точек во входной и выходной плоскостях, Np–Nр–1 – число лучей пришедших M в точку (отсчет) ξp , ∑ Np = N – общее число лучей. p=1

Очевидно, что в результате дискретизации в некоторых отсчетах суммарная интенсивность окажется несколько больше требуемого значения, в других – меньше, однако необходимым является выполнение равенства:

MN

∑ I В ( ξ k ) = ∑ I 0 ( x k ),                    (23)

k = 1              k = 1

Здесь и далее предполагаем, что ∆ x = ∆ ξ – шаги сетки на входе и выходе одинаковы.

Для иллюстрации метода на рис. 8-10 приведены примеры расчета ГОЭ формирующих различные распределения интенсивности в выходной плоскости. На рис. 8a, 8b, 8c показаны профили интенсивности формируемые элементами; на рис. 9a, 9b, 9c показан ход лучей в зонах соответствующих элементов; на рис. 10a, 10b, 10c показан коэффициент преломления элементов на расстоянии l =10 мм от входной плоскости.

Параметры расчета: ширина элемента H вх = 10 мм, длина элемента L = 30 мм, ширина выходного пучка h вых = 2 мм.

I

4. Расчет ГОЭ для фокусировки в заданное распределение интенсивности

Для расчета ГОЭ, фокусирующего лучи в заданное распределение интенсивности в выходной плоскости, можно разбить элемент на зоны, число которых будет соответствовать количеству отсчетов в выходной плоскости. Внутри каждой такой зоны (рис. 7) лучи будут идти в соответствии с уравнением (8), В подобном составном ГОЭ коэффициент преломления n уже будет зависеть от переменных x и z, то есть n ≡ n ( x,z ), но внутри зон он будет удовлетворять выражению (7).

0 III— 012

X, мм

а)

0          1

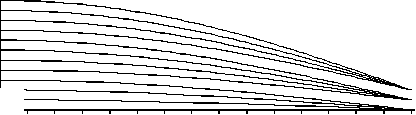
0    2    4    6    8   10   12   14   16   18   20   22   24   26   28   30

Z, мм.

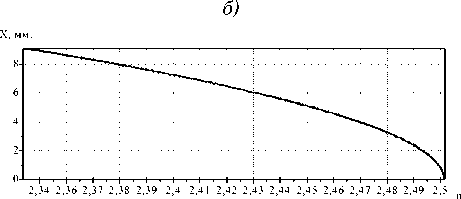
X, мм.

I

в)

Рис. 8. Исследование составного ГОЭ, формирующего равномерное распределение интенсивности:

• а) распределение интенсивности в выходной плоскости; б) ход лучей в зонах (всего 12 лучей);

• в) показатель преломления n на расстоянии l=10 мм от входной плоскости.

  

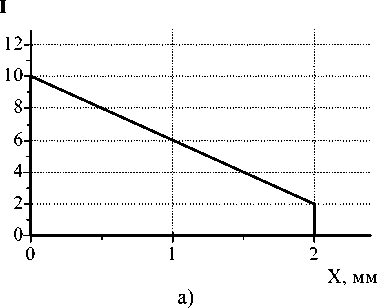
X, мм.

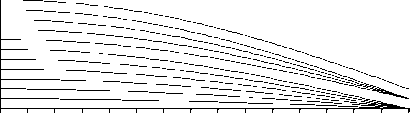
0    2    4    6    8   10   12   14   16   18   20   22   24   26   28   30

Z, мм

б)

в)

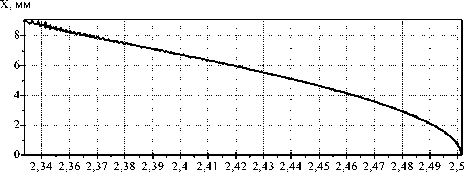
Рис. 9. Исследование составного ГО, формирующего линейно убывающее к краю элемента распределение интенсивности: а) распределение интенсивности в выходной плоскости; б) ход лучей в зонах (всего 12 лучей); в) показатель преломления n на расстоянии l=10 мм от входной плоскости.

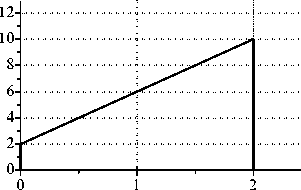
X, мм а)

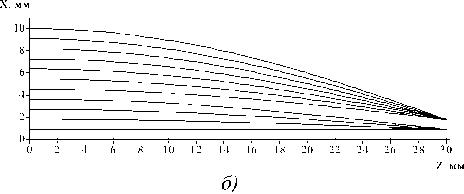
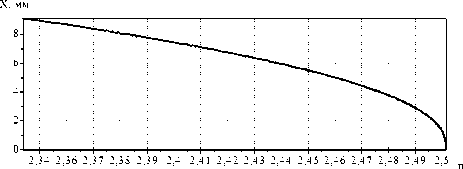
в)

Рис. 10. Исследование составного ГОЭ, формирующего линейно возрастающее к краю элемента распределение интенсивности: а) распределение интенсивности в выходной плоскости; б) ход лучей в зонах (всего 12 лучей); в) показатель преломления n на расстоянии l=10 мм от входной плоскости.

Заключение

Получены следующие результаты:

• •    получено ограничение на апертуру ГОЭ, фокусирующего плоский пучок в точку;

• •    обобщено решение для случая плоского входного фронта и фокусировки лучей в произвольной осевой точке;

• •    проведено численное моделирование и исследована зависимость СКО от изменения параметров разностной схемы, для расчета лучей в ГОЭ, показатель преломления которого зависит от одной поперечной переменной;

• •    предложен метод расчета составных ГОЭ, формирующих заданное распределение интенсивности в выходной плоскости.