Расчет спектральной динамики системы с квадратичным электронно-колебательным взаимодействием

Появление в последние десятилетия техники, позволяющей инициировать и контролировать электронные процессы, протекающие на временах порядка 10 ^–12 ÷ 10 ^–14 с, поставило и новые нетривиальные вопросы о поведении физических систем в таких условиях. Поэтому теоретическое изучение динамики быстропротекающих процессов, сопровождающих процессы переноса заряда, является одной из актуальных проблем современной химической физики. К числу таких процессов относится, например, формирование спектра поглощения иона в процессе его сольватации.

Теория зависящих от времени спектров, связанных с изменением распределения электронной плотности, когда при переходе меняется равновесное положение ядер, построена ранее [11; 16]. Основной вывод этих работ состоит в том, что в случае сильной связи электронных состояний со средой, спектр, не меняя своей формы, эволюционирует к своему стационарному положению, если длительность импульса возбуждения много меньше характерного времени ядерной подсистемы (например, время релаксации среды). Закон временной эволюции центра тяжести спектра повторяет временную зависимость классической корреляционной функции флуктуаций электронных энергетических уровней [3]. Под спектром понимается вероятность оптического перехода на частоте ν на достаточно коротком интервале времени из одного электронного состояния в другое [ibid.].

В данной работе ставится задача установить, остается ли этот вывод справедливым, когда при электронном переходе меняются не только равновесные положения, но и частоты колебаний.

Модель

Для количественного описания влияния изменения кривизны электронных термов на динамику электронно-колебательной системы будем использовать двухуровневое приближение, рассматривая только два состояния: основное состояние 2 и первое электронно-возбужденное состояние 1 , заселяемое вследствие фотовозбуждения (рис. 1). Эта ситуация реализуется, например, при возбуждении полосы с переносом заряда в донорно-акцепторных комплексах. Рассматриваемая система описывается гамильтонианом:

где

H =

f H i ^A i ( t )) ^ A , ( t ) H 2 J

H1 =Z®q (b+ bq + 2) , H2 VQq (Q Cq + 2 )-AE —

q

q

гамильтонианы колебательной подсистемы в состояниях Ц и |2^ соответственно. Здесь AE - разность минимумов потенциалов начального и конечного электронных состояний, т и Q -qq частоты нормальных колебаний термостата с индексом q, bq (bq) и Cq"Cq - операторы рожде- ния (уничтожения) колебательных квантов в состояниях 1 и 2 , связанные унитарным преобразованием

A             (^ + ^ )

Vq =

1 (^ q — ®q )

Нетрудно показать, что гамильтониан H ₂ можно записать в виде:

H 2 Z x (b+ bq + 2 ) + A (bq + b+ ) + Bq (bq + b )

^{2 q}

-A E , B q =

qX X

4 ω q

где A_q и B_q – константы, характеризующие интенсивность линейного и квадратичного электронно-колебательного взаимодействия. Матричный элемент электронного перехода в (1) полагается равным A , ( t ) = A exp ( ivt ) , где v — частота электромагнитного поля, вызывающего переходы между состояниями 1 и 2. Далее предполагается, что A не зависит от координат ядерной подсистемы, то есть выполняется приближение Кондона. Влияние зависимости электронного матричного элемента от ядерных координат на динамику электронных переходов и условия применимости приближения Кондона обсуждалось в работах [2; 15].

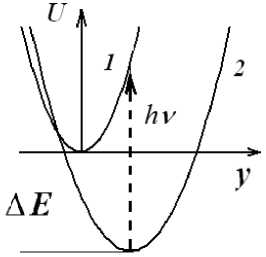
Рис. 1. Профили поверхностей потенциальной энергии колебательной подсистемы

вдоль координаты реакции y для начального 1 и конечного 2 электронных состояний;

ν - несущая частота электромагнитного поля, вызывающего переходы между состояниями 1 и 2

Эволюция рассматриваемой системы описывается уравнением Лиувилля для статистического оператора ρ :

'dP ki = [ ^H , P 1,, k , l = >,2. dt kl               _kl

Здесь и далее используется система единиц, в которой постоянная Планка h = 1 . Существует несколько подходов, позволяющих аналитически решить это уравнение во втором порядке теории возмущений по матричному элементу A [1-17]. Далее будет использован метод функциональных производных, ранее подробно изложенный для данного класса задач в работах [5; 6; 12].

Если система в начальный момент времени находилась в состоянии 1, то вероятность перехода — ^ |2^в единицу времени можно представить в виде

2 t

W ( v , t ) = A_ Re f e ^VT G ( t )) dT .

Здесь ... означает усреднение с гамильтонианом H 1 по ансамблю Гиббса,

G G(t)) =( T exp <-i J

\ I T

1 *

–

производящая функция, зависимость операторов от времени A H ( t ) = H ₂( t ) - H 1 ( t ) определяется гамильтонианом H ₁ .

Методика расчета производящей функции

Для расчета производящей функции G ( t ) введем формально в статистический оператор

Р о = [ Sp exp ( - ^e H 0 ) ] ¹ exp ( - ^e H 0 )

добавочную Т -экспоненту

^„

р' = T exp ]-г J ^ fq (t) (bq (t)+ b+ (T ))dT *, . о q                                                    , зависящую от классических полей fq (t), которые в конце расчета полагаются равными нулю.

В формуле (8) гамильтониан имеет вид

H0  У^. (c+ cq + 2) ,

q

a A / x 1 (^ + to )

c q = b q u q ^{- b} + v q ⁺ - q T^ ( u q ⁺ v q ) , u q =     /       , v q

-

-

to q )

.

ϖω qq

Далее усреднение производится со статистическим оператором р = р0р'^р'^ _q*. Среднее значение для произвольного оператора A , содержащее хронологические комбинации операторов b _q ( t ) + b q ( t ) , определяется соотношением [6]

t п[ь„ (ta+ь+ (ta]A =n К (o+ь+ (t^ о

г

δ

+ i-----7—T

^f q i ⁽ t j

A 0

=nm

0 ,

где m_q ( t ) = i 5 ln р'/5 f_q ( t ) - логарифмическая производная.

В формуле (10) сначала вычисляются функциональные производные и только затем классические поля fq (t) полагаются равными нулю. Учитывая, что матрица плотности в пространстве ядерных степеней свободы факторизуется р'(t) = П рq (t), далее будем рассматривать q только одну степень свободы, опуская индекс q. Переходя к операторам с, с+, перепишем уравнение для ρ ' в следующем виде:

i dр(t)=[ g ч t) c++g (t) c+Q (t)] р х t), где

^{p (} t ) = ^р t ^)exp

<

—.

t.

i J Q ( t ) d T ^ , g(t ) = f ⁽ t ) g ⁽ t ), о                ,

/ itot ,        - itot\ g (t) = ( ve + ue ),

Q (t) = - — (u + v) f (t) (eto + e- itot), а оператор ς(t) удовлетворяет уравнению id^T = Г % t) c + + g( t) c 1 ^ (t).

dt LJ

Нормально-упорядоченное решение последнего уравнения было найдено в работе [14]: q( t) = eA(t) eC(t)c + eB(t)c, где t                     τ1                                                 tt

A(t ) = - J dT i g(T i ) J dT 2 g * ( T 2 ), B ( t ) = - i J d^g(T i ), C ( t ) = - i J dT i g o T J .

00       00

Выполняя усреднение q (t ) и переходя к пределу t ^ да , получаем:

дада

^^ ( t ^ да)^ = exp <

^- Т J f ^{( T} 1 ) d ^T 1 J f ^{( t} 2 ) d ^T 2 [ ^{0 ( t} 1 - ^T 2 ) ( ( N ⁺ 1 ) g ^{( T} 1 ) g * ^{( T} 2 ) ⁺

+Ng*(T1)g(T2)) + 9(T2 - T1) ((N + 1) g(T2)g4T1) + Ng*(T2)g(T1)) J} , где N = [exp(—в) -1] 1.

Выражение для производящей функции (7) можно записать следующим образом:

GG(t)) = exp{-i(E^ - NE)(t - t)}^(t,t)^, где

r 2

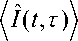
= exp <

t

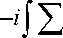
τ ^q

^Aq m q ^{( T} 1 ) ⁺ i

V

5  )

^f q ( T 1 ) _v

^{+ B}q m q ^{( T} 1 ) ⁺ i

V

^f q ( T 1 ) J

dT 1 ^ ,

= x

q

A q ω q ° 2

– энергия реорганизации ядерной подсистемы во втором электронном состоя-

нии. Учитывая, что I(t ,T) = П Iq (t ,T), далее, как и раньше, будем рассматривать только од-q ну колебательную степень свободы, опуская индекс q. Введя обозначения:

t ab = J a(т1)b(т1)dr1,

τ

t aA = J a (т1) A (т1, t1)dr 1,

τ

t

AB = J A(t₁, T ₁) B ( т 1 ,1 2 ) d T 1 , τ

t

Aa = J A(t₁, T ₁) a ( т 1 ) d T 1

τ

запишем I ( t , τ ) (12) в следующем виде:

I = ^exp⁽ - 2

ˆ

A J—. A     . Ax црц - ia^),

где

δ ц/(т1) = m(т1) + i , F = 2гБ6(т2 - T1), a = A. δf (τ1)

Представляя (11) в виде интеграла Фурье

I = / ¹    I" D^ exp

Tdet p J " ^p

,

получаем

I =

J m exp < - ¹ ^F "‘^ - ¹ ( ^ - a ) D ⁰ ( ^ - a ) + im ( ^ - a ) > .

Выполнив обратное преобразование, окончательно получаем:

I =

exp l—^m — iaD °)(F ' + D °) (^ — iaD °) — ^D ° a — ^a I .

Последнее выражение можно привести к виду:

I = exp <

-2 aDa - iaM -2 mFM - — Sp ( FD ) > 2                2          2 ^{x 7}

где неизвестные функции D

и M находятся из уравнений:

D = D0 - FD0 D, M = m - FD0 M.

Здесь m ( t ) и D ⁰( t ₁, t ) уравнениями:

-

первая логарифмическая и вторая производные, определяемые

m ( t ) = i^ln^P- = - ^aAU + vA(e^{i m t} + e i ^ t - 5f ( t )       ^ ^{(     )(}           )

X

—,

■ i J f ^{( т} 1 ) d^T 1 ^ ⁽ t ^{- т} 1 ) ( ( N ⁺ 1 ) g ⁽ t ) g *^{( т} 1 ) ⁺ Ng Ч t ) g ^{( т} 1 ) )⁺

⁺ 6 ^{( t} 1 - t ) ( ( N ⁺ 1 ) g ^{( T} 1 ) g * ⁽ t ) ⁺ Ng * ^{( T} 1 ) g ⁽ t ) ) ,

D ”( ' ■ , ‘ ) = i ^vS ^N '' t - t , ) ( ( N + ' ) g ( t ) g ‘( ' ■ ) + Ng ‘( ' ) g ( t , ) ) +

δ f ( t ₁)

+ 6(t , - t ) ( ( N + , ) g ( t , ) g * ( t ) + Ng * ( t , ) g ( t ) ) ] .

Формула (15) определяет производящий функционал для корреляционных функций смещений от положения равновесия ядерной подсистемы и, в принципе, решает задачу о динамике спектра системы с квадратичным взаимодействием в процессе релаксации. Выражение для I ( t ) является гауссовым функционалом, который и с течением времени остается гауссовым.

Второй кумулянт этого функционала D ( τ ₁, τ ₂ | t , t ₁) , который определяет частотную дисперсию, не одинаков для стационарного и нестационарного спектра. Отсюда можно сделать вывод, что в процессе эволюции форма спектра, по отношению к стационарному спектру, меняется. Закон эволюции центра тяжести спектра определяется первым кумулянтом и, по отношению к стационарному спектру, содержит единственное дополнительное слагаемое M ( τ | t , t ₁) , которое, по сути, и описывает эволюцию среднего значения смещения положения системы в начальный момент времени от положения равновесия в потенциале, зависящем от времени.

Для рассматриваемой модели (1)–(3) выражения для кумулянтов D ( τ ₂, τ ₁ | t , t ₁) и M ( τ | t , t ₁) могут быть найдены в явном виде. Запишем для них уравнения в развернутой форме:

D (т 2,т, 1t, t1) = D 0(т 2,т1) - 2 iB J D 0(т 2, т 3) D (т 3, т,1t, t1) dT 3, t1

M(т 1 1 , t , ) = m ₀( t ) - 2 iB J D ⁰ ( r , r , ) M ( r , 1 1 , t , ) dr , ,

t

t ₁

где m о = m \ f = 0 = - a

ei®t + e—t®t)/^ , а функция Грина D0(т2,т,) удовлетворяет уравнению d2

(—у + to ²) D 0 ( t ₂, L ) = - 2 ito8(t ₂ - t ) .

dt ₂ 2               2 1                2 1

Используя последнее соотношение, уравнение (15) для D ( τ ₂ , τ ₁ | t , t ₁ ) можно свести к дифференциальному

( dT 2     J

—у + Q ^D (T 2 ,T ,\ t , t , ) = ^{- 2} lto5(T 2

( ^dT 2       J

- T , ),    t , <  T ₂ <  t .

Решение уравнения (18) D ( τ , t | t , t ₁ ) ищем в виде:

D(t,t \ t,t,) = ^,(t, t,)eito(T t) + x,(t, t,)e ito(T t), т > t, D(t, t \ t, t,) = Ф2 (t, t,)ein(r -t) + X2 (t, t,)e-in(r -t), т < t.

Связь между искомыми функциями находим из условия непрерывности функции

D(t, t \ t, tj) при т = t и известной величины скачка первой производной d-D(т,t | t,ti) T^t+o -d D(т,t | t,ti) T^t-о = —2®.

ττ

Отсюда находим

( ® + О )ф₂ + ( ® - Q ) x — 2 ®      ( ® — Q ) ^ + ( ® + Q ) X + 2 ®

Ф1 =----------------, Xi =----------.

2ω2

Подставив решения в исходное уравнение с учетом связи между функциями и приравняв коэффициенты при одинаковых экспонентах, получим систему двух линейных алгебраических уравнений для определения неизвестных функций, решив которую получаем:

D(t,t1t,ti) = 0(t,ti)/Dt(t,ti), где

D t ( t , t _i ) = ( 2 N + i ) UVuv ( e ® ⁽ t ⁺ t¹ ) + e - i ® ⁽ t ⁺ t¹ ) ) ( e‘ ^Q( t - t ¹ ) - e -‘^Q( t - t¹ ) ) - 2 N ( N + 1 ) + + ( N ² u ² - ( N + 1 ) 2 v ² ) e i ® ⁽ t ^- t¹ ) ( U²e ^-‘ ^Q( t ^- t¹ ) - V ²e‘ ^Q( t ^- t¹ ) ) +

+ ( ( N + 1 ) 2 u ² - N ² v ² ) e ^- i ® ⁽ t ^- t¹ ) ( U ²e‘ ^Q( t ^- t¹ ) - V²e ^-‘ ^Q( t ^- t ¹ ) ) ,

0 ( t , t ₁) = ( U + V )(2 N + 1) uv U ( e "i® ⁽ ‘ ^{+ t i )- i Q(} ‘ ^- ' + e i ® ⁽ t ⁺ t ^{i )+ i Q(} t ^- t ⁱ ) ) -

— V ( e i ® ⁽ t ⁺ t i ^)- i ^Q( t ^- t i ) + e ^- i ® ⁽ t ⁺ t i ⁾⁺ i ^Q( t ^- t i ) ) — ( N ² u ² — ( N + 1) 2 v ² ) e i ® ⁽ t ^- t i ) ( Ue ^- i ^Q( t ^- t i ) — Ve ^Q( t ^{- t} i ⁾ ) +

+ ((N +1)2 u2 -

N ² v ² ) e ^- i ® ⁽ t ^- t i ) ( Ue i ^Q( t ^- t i )

- Ve ^- i ^Q( t ^- t i ) )

Решение уравнения (17) для функции M ( τ | t , t ₁) ищем в виде:

M (t 1 1 , t i ) = _W( t , t i ) e ® ^{( T} - ' ) + X i (t , t i ) e ® ^{( T} - ' ) ( т > t ),

M ( t | t , t ) = ^ 2 ( t , t i ) e«^T - ' ) + X 2 (I , t i ) e«^T - ' ) ( т <  t ).

Используем непрерывность решения и его первой производной: ф ₁ + x _i = Ф ₂ + Х ₂ , ®(ф ₁ - X _i ) = Q ( ^ ₂ - X ₂ ) . Подставив решение в уравнение (17) и решив соответствующую систему алгебраических уравнений, находим:

^2 = p ( t, ti)/Dt( t, ti), X2 = q( t, ti)/Dt( t, ti), где

p ( t , t _i) =- i ^aAL { ( Q- ® ) ( nu - v ( N + 1 ) ) e ^{i (} t ^- t ^{1 )Q- i} ® t ¹ - ( Q + ® ) ( ( N + 1 ) u - Nv ) e ^{i (} t ^{- I i )q+} ® ^{1 1} -

-(u + v)[(П-®)((N +1)u2 -uv(2N +1) + Nv2)e-i®t --(Nu2 -uv(2N +1) + (N +1)v2)(Q + ®)e® ]},

q ( t , t 1 ) =- i "t Aa { ( Nu - v ( N + 1 ) ) ( ^Q + ^Ю ) e - i ⁽ t - t ¹ ) °- " - ( ° - ^Ю ) ( ( N + ¹ ) u - Nv ) ^e — i ⁽ t - t ’ ) “+ i^ -

-(u + v) ((N +1)u2 -uv(2N + 1) + Nv2)(° + to)e-itot -

- ( Nu ²

- uv (2 N +1) + (N +1) v2

) ( °- to ) e i ^{to t} ] } .

Для того чтобы полностью определить функционал (14), необходимо найти D ( τ ₂, τ ₁ | t , t ₁) при разных временах τ ₁ и τ ₂ путем решения уравнения (15). Однако проще поступить следующим образом. Проинтегрировав его по τ ₁ , получим уравнение (16), только с другими начальными условиями. Фактически это уравнение для первого кумулянта стационарного спектра. Свободный член после интегрирования имеет вид:

где a1 (t) = A (((N +1) u2 + Nv2) e-ltot - (2N +1) uv (eitot - eltot’) - (Nu2 + (N +1) v2) e to'), ω a2 (t) = A(-(Nu2 + (N +1) v2) eitot + (2N +1) uv(e"tot - e-itot’) + ((N +1) u2 + Nv2) eltot’). ω

Соответственно решение ищем в виде:

M (t | 1 , t ’ ) st = ^ ’ ( t , t ’ ) e ^T U X 1 (t , t ’ ) e ^{T }} --при т >  t ,

M ^{( т} I t , t 1 ) st = ^ 2 ⁽ t , t 1 ) ^e i ° ^{( T} - t ) ⁺ X 2 ⁽ t , t 1 ) ^e i ° ^{( T} - t ) —° ?- при т <  t .

Связь между неизвестными функциями находим, как и прежде, из условия непрерывности решения и его первой производной при т = t :

^ф 1 ⁺ Х 1 - ² to = ^ 2 ⁺ Х 2 - ² ^ top ^to ( ^ 1 - Х 1 ) = ° ( ^ 2 ^- Х 2 ) .

Аналогично предыдущему случаю, подставляем решение в исходное уравнение, приравниваем коэффициенты при одинаковых экспонентах и получаем алгебраическую систему уравнений, решив которую находим:

^2 (t, t’ ) = (bo (t, t’)+b’ (t, t’) a1 (t, t’) + b2 (t, t’) a2 (t, t1)) / Dt (t, t1), X2 (t, t’ ) = ( co (t, t’) + c1 (t, t’) a1 (t, t’) + c 2 (t, t’) a 2 (t, t1)) / Dt (t, t1), где b0(t,t1) = -AA(2юfiT ){uv(2N + 1)(e/Q(‘ - ^Ш-ю + Q)e-^(t + t-^ + Q)e"(t+t°) +

+ ((N +1)2 u2 - N2v2) e-^(t-t1) ((ю + Q)e"’1t-t1) - to + q) +

+ ( N ² u ² - ( N + 1) 2 v ² ) e " ⁽ t - ^{t 1 )} ( ( - ю + Q ) e i ^Q( t - t^{1 1} + ю + q ) -

• - 2 N ( N + 1) Q ( e ^{l Q(} t ^-l ■ 1 ) } ,

b ₁ ( t , t₁ ) = - 2 Q { ( 2 N + 1 ) uv ( - ю + Q ) ( e ^{- i m t} - e‘ ^Q( t ^- t ^{1 )- ю 1} ) +

+ (ю + Q)((Nu2 + (N +1) v2)eю -((N +1) u2 + Nv2)e1 Q(t-t1)+ю1)}, b2( t, t1) = 2Q{(-" + Q)((( N +1) u2 + Nv2)e" l"t-( Nu2 +(N +1) v2) e‘Q t - t1)-^) +

+ (ю + Q)(2N +1)uv(eю -e*Q(t"t1)+imt1)}, c o( t, t1) = -lA (Чю-ю ) {uv (2 N +1)( e-‘Q t - t   Ню + Q)e"^(t+M-®+ Q) el"(t+10] +

• +    ( N + 1) 2 u ² - N ² v ² e ^{- 1} " ( t ^- t ¹ ^ ( ( Q- " ) e ^{- 1 Q(} t ^- t ¹ ^ + ю + q ) +

• +    ( N ² u ² - ( N + 1) 2 v ² ) e ^{/ ю (} t ^- t ^{1 j} ( ( ю + Q )e ^{- 1 Q(} t ^- t ^{1 j} - ю + q ) -

• - 2 Q N ( N + 1) ( e ^{- 1 Q(} t ^- t ^{1 }} + 1 ) } ,

c ( t , L ) = —U(2 N + 1) uv ( ю + Q)(e - ^ t - e ^{- l Q(} t ^{- t 1 )- l ю t 1}) +

• 1    , 1       2Q{(         ) (         )(                         )

• + ( Q - ю ) ( ( Nu ² + ( N + 1 ) v ² ) e ^ t - ( ( N + 1 ) u ² + Nv ² ) e ^{- l Q(} t ^{- t 1 )+ l ю t 1} ) } ,

c ₂( t , t ₁) = - 2 Q { ( ю + Q ) ( ( ( N + 1 ) u ² + Nv² ) e - ^ю - ( Nu ² + ( N + 1 ) v ²) e ^{- l Q(} t - t ^{1 mt}' ) +

+ uv ( - ю + Q )( 2 N + 1 ) ( e ^ю - e ^{- l Q(} t - t ^{1 )+ l m t 1} ) } .

Подставив найденные решения в выражение для I_q ( t , t ₁) (14) и выполнив интегрирование, окончательно получаем:

П I q ( t . t 1 ) = П

q

q

D q ( t , t 1 )

• ^A q U M q ¹^¹ 1 q ⁽ t , t 1 ) ⁺ aM 2 q ⁽ t , t 1 ) ⁺ a ² M 3 q ⁽ t , t 1 ) exp <  l ( t - 1 .) +-- q------------------q-------------------q-------

(Q q^V                         D q ( t , t 1 )                 J

где

A ²

M 1 q ( ‘ , ‘ 1 ) = ^-N q ( N q + 1 ) ( 0 i “ q ⁽ ‘ ’ ⁴ ’ - e ’ i “ q ⁽ ‘ ’ ‘ 1 ’ ) +

+ '/ AT ( ² N q + 1 ) U q V q ( e   ‘

^{2 Q} q ^Q q

' q ⁽ ‘ i + ‘ )W ’ i ^Q q ⁽ ‘ ^- ‘ 1 )       i ^Q q ⁽ ‘ ^- ‘ 1 )    ^\

+ e lie + e — 2 -

A ²

— ₍₎ ( U q + V , ) ( N 2 U ^Q q

q

— ( N q + I ) v q ) ( ( U q + V q ) e"

—

U q e

.^— i ( ^Q q ' ) ⁽ ‘ ^— ‘ 1 )

—

V e i ( ^Q q ⁺ ' q ) ⁽ ‘ ^— ‘ 1 ) )

+

A ²

+ 752( U q + V )(( ^Nq + O’ U q

^Q q

—

22 qq

U_q + V_q ) e ^— i ' q ⁽ ‘ ^— ‘ ¹ )

у _e ^— i ^{( q} q + 'q ⁾⁽ ‘ ^— ‘ 1 )

V q e

—

U e i ^{( q} q ^— ' q ⁾⁽ ‘ ^— ‘ 1 ) )

A ²

^M 2 q ⁽‘ , ‘ 1 ) = ^— ' Q ( ^Uq ^{+ V}q ) { ( ^Nq u q ^{+ ( N}q ^{+ 1)} v q ’ ^{(2 N}q ^{+ 1)} u q v q )( u q ⁺ v q ) e q ⁺ + ( N_qu — ( N + 1) v ) e ^{i m} q ‘^{1 f} U + V — V e^m q ⁽‘^— ‘ — U_qe i ^Q q ⁽‘^— ^ll

A ²

— —q^Ua + V ) (( N_a + 1) u ² + N_av ² — (2 N + 1) u_av_a\(u_a + v_a Ie q +

' Q \ q q J \ q              q ^v q ^q q q)\ q q)

+ЙМ -Nv )eiюqt1 fU +V -UeQq(‘—‘1)-Ке—iQq(‘—‘1)11, 11 q       i q^q         q q J I q q q                       q11 n                    q (^q ^q )                   2           2    /nt               \ (т     i(Qu —')(‘—‘1)    тт2 — i(Qu+'«(‘—‘1) \

M3 Л ‘, ‘л) =  q .      ((No +1) u + Nnv — (2 N +1) uv ) U 2e ( q  q)(  1)— V 2e ( q  q)(

3 q 1            ω 2             q              qq q q

+ ^{Aq (} uq + ^Vq ) ( N u 2 + ( N + 1) v 2 — (2 N + 1) u   ) U 2e ^— i ( ^Q q ^—' q ^{) (} ‘ ^— ‘ 1 ) — v 2e i ( ^Q q +' q ^{) (} ‘ ^— ‘ , )\ _

ω2 q q q q q q q qq

—

A q ^{2 (} u q ⁺ v q ^{) 2}

2 ω ₁

U q V q ( е^Ю q ⁽ ‘ ’ ‘ 1 )

—

e

— i Q _q

( ‘ ^— ‘ 1 ) ) (

e i ' ( ‘ + ‘ 1 )

+ e

A ²

,^{— i m} q ⁽ ‘ ⁺ ‘ 1 ) ) _— ²¹ q ( 2 n

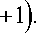
Подставляя выражение (19) в уравнение (6), для W ( ν , t ) получаем окончательное решение поставленной задачи.

Далее рассмотрим один частный случай, когда отсутствует частотный эффект, то есть Q _q = '_q . В этом пределе производящая функция описывается выражением (19), где

D_q ( ‘ , ‘ ₁) = 1 , а функции (20)-(22) имеют хорошо известный вид [11]:

A ²                                 A ²

^M 1 q ⁽ ‘ , ‘ 1 ) =^— ^ ( ^{2 N}q ⁺ ^^ ’ cos ' q ( ‘ ’ ‘ 1 ) ] ^— i "Л sin ' q ( ‘ ’ ‘ 1 ) ω_q ²                                ω_q ²

2 A q ²

^Si n ' q ‘ 1 ) , ^M 3 q ⁽ ‘ , ‘ 1 ) = ⁰ .

^M 2 q ⁽ ‘ , ‘ 1 ) = ⁺ i ----( ^Si n ' q ‘ ^—

ωq

Этот результат демонстрирует, что полученное нами выражение для производящей функ- ции полностью согласуется с известными в литературе результатами.