Расчет спектральных дифракционных решеток

ДОЭ создаются, как правило, для работы с излучением одной заданной длины волны. Для боль-

шого количества прикладных задач, включающих задачи распознавания, обработки изображений, оптической связи, измерения температурных характеристик объектов, цветной печати и фотографии, требуются ДОЭ, позволяющие работать с излучением различных длин волн. Для работы с излучением различных длин волн известны фазовые дифракционные решетки (color separation gratings), позволяющие разделить 3 плоских пучка с длинами волн

на случай общего соотношения длин волн и разделения большего числа длин волн. Отметим, что решетка (2) обращает в ноль функцию невязки, представляющую отличие функций комплексного про-

пускания квантованных призм от комплексных амплитуд формируемых пучков для плоских пучков с длинами волн (1):

F ⁽ Ф 1 ,..., Ф N ^{) =} ЁЁ exp | i 2П¹ ■ j

1 N

1 =- 1j = 1

^А О , ^А + 1 = ^А О _м , ^А - 1 = ^АО _м , N + p       N - p

exp l i

N + p ■ 1

N

где N, p – взаимно простые числа, по -1, 0 и +1 дифракционным порядкам [1-4]. В дальнейшем будем называть такие решетки спектральными. Спектральная решетка имеет на периоде N ступенек равной ширины. Высота ступенек определяется по формуле

А di = 7—0-rmodn (a ■ i), i = 0, N -1,          (2)

⁽ n о ^- 1 )

где a - целое число, определяемое по формуле

где ф j = - n ■ mod _N ( a 1 j ), j = О, N - 1

соответствуют фазовым набегам решетки (4) для длины волны Х _о. Учитывая вышеприведенную связь функции невязки (7) с решеткой (2), предлагается

искать решетку для разделения трех произвольных

длин волн

^А О , ^А + 1 = ^А О c + 1 , ^А - 1 = ^А О c - 1

по порядкам ±1 из условия минимума функции невязки

a = ( N ■ z + 1 ) / ( N + p ), z e Z .

Поскольку числа N и р взаимно простые, то уравнение (3) всегда имеет решение в целых числах по теореме о наибольшем общем делителе. Пренебрегая дисперсией материала решетки, определим связь фазового набега ф с высотой рельефа решетки для длины волны А в виде:

ф = 2^- ■ ( n о ^{- 1 ) 1} d i , i = ^{0 N - 1.               (4)}

А

Согласно (4), решетка (2) для плоских пучков с длинами волн (1) формирует следующие фазовые набеги по модулю - л :

Ф о = о, ф ± 1 = + — , i = о, N - 1.          (5)

Согласно (5), для длины волны Х _о фазовый набег равен нулю и, следовательно, данная спектральная компонента направляется в нулевой порядок. Для длин волн Х + 1 фазовые набеги (5) соответствуют фазовым функциям призм, квантованных по N уровням. Это обеспечивает разделение длин волн Х ± 1 по порядкам ± 1. Вследствие квантования доля энергии спектральных компонент Х ± 1 , направляемая в порядки ± 1, описывается функцией

E ( N ) = Sinc ² ( п / N ) .                         (6)

Рассмотрим расчет спектральных дифракционных решеток, обобщающих известные решетки (2)

1 N

F ⁽ Ф 1 ,..., ф N ) = ЕЕ 1 =- 1j = 1

I - п exp l i — 1 ■ j

I N

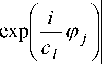
, c о = ¹

Естественным технологическим ограничением при синтезе решетки является ограничение на максимальную высоту профиля. Отметим, что высота профиля решетки (2) превышает в N раз высоту рельефа обычной решетки для работы с излучением одной длины волны Х _о. Поэтому при больших значениях N в (1) или при общем соотношении длин волн целесообразно искать профиль спектральной решетки из условия минимума функции невязки (10) при ограничении ф j e [ О,2пК ] , j = О, N , где значение K определяет максимальную высоту профиля. При

этом значения ф j несложно найти простым перебо-

ром из условия минимума невязок

2 ^п . / sin — j ^Е N

p =- 1

V

1L. )

² cp J

^ min,

где ф j e [ О, -nK ] , j = 1, N , c _о = 1. В качестве приме-

ра была рассчитана решетка для разделения длин волн Х _о=1,55 мкм, Х +! =1,31 мкм, Х . ₁=1,625 мкм, использующихся в системах телекоммуникаций. Сле-

дует отметить, что приведенные длины волн не удовлетворяют соотношению (1);

Л ₀   1,55 _ 6 Я ₀     1,55   20

Л ₊₁ = 1,31 ~ 5, Л - 1 = 1,625 ~ 21.

Расчет решетки проводился при K=16, N=8 и ф j е { 2п-l j , l j = 1,2,..., K } . Рассчитанные высоты ступенек профиля равны

( d ! ,..., d 8 ) = ^L55 ( 0,1,7,8,8,14,15,16 ) мкм . (12) ⁽ n о ^- 1 )

Выбранный вид значений ф j = 2п ■ l j , l j <  K дает для длины волны 1 ₀ фазовый набег по модулю 2п равный нулю. Поэтому пучок с длиной волны 1 ₀ направляется в нулевой порядок. Для оценки энергетической эффективности решетки были рассчитаны интенсивности ± 1 порядков для длин волн 1 ± 1 .

с

■L -2 п

^E sin -n p j

p = 0

п

V

N

^ф , )

2c

² c p J

^ min, c 0 = 1, j = 1, N .

В качестве примера была рассчитана решетка для разделения пяти длин волн 1 =1,55 мкм, 1 - ₂= 1 ₀(23/19), 1 -1 = 1 0 (21/19), 1 +1 = 1 0 (21/23), 1 +2 = 1 0 (21/25) по порядкам 0, –2, –1, +1, +2. Расчет решетки проводился при Ф j = 2 п ■ l j , l j <  K , K=10 и N=16. Рассчитанные высо-

ты ступенек профиля равны

( d 1 ,..., d 16 ) = /55 _и ( 0,1,1,2,3,3,4,

^{( n} 0 ^{- 1 )}

5,5,6,7,7,8,9,9,10 ) мкм.

I Л ± 1 ) =

I exp|

,

где ф ( x ) - фазовая функция решетки при 1 = 1 ₀. Согласно расчетам, решетка (12) направляет 100% энергии спектральной компоненты 1 =1,55 мкм в 0-й порядок, 86,7% энергии спектральной компоненты 1 +1 =1,31 мкм в 1-й порядок и 80,1% энергии спектральной компоненты 1 -1 =1,625 мкм в -1-й порядок.

В качестве следующего примера была рассчитана решетка для разделения длин волн 10=1,55мкм, 1+1=1(21/23)=1,4152мкм, 1-1=10(21/19)=1,7132мкм, удовлетворяющих соотношению (1) при N=21 и p=2. При расчете по аналитической формуле (2) решетка будет иметь 21 ступеньку на периоде при макси мальной высоте ступеньки dmax = 20 , , мкм . С (n 0 - 1)

целью упрощения технологических параметров была рассчитана решетка из условия минимума невязок (11) с 8-ю ступеньками на периоде при K=8 и Ф j = 2 п ■ l j , l j <  K . Рассчитанные высоты ступенек

Для решетки (16) доли энергии спектральных компонент Л ц, Л ± ₂ , направляемых в порядки -1, +1,-2,+2 составляют 96,3%, 96,3%, 80,4% и 85,9%, соответственно.

Использованный метод расчета спектральных решеток может быть также использован для расчета сложных дифракционных оптических элементов (ДОЭ), выполняющих заданные преобразования волновых фронтов для излучения различных длин волн. Будем считать, что микрорельеф ДОЭ опр ед елен на двумерной сетке отсчетов ( i , j ) i , i = 1, N . Предположим, что для длин волн Л ₀, Л_п = Л₀c_n , n = 1, L ДОЭ должен сформировать пучки с фазовыми функциями ф ₀( i , j ),..., ф_L ( i , j ). В

этом случае значения ^j = — ■ ( n ₀ - ] ) ■ d, опреде- Л 0

ляющие высоту микрорельефа ДОЭ, определяются из условия минимума невязок

L

E sin ²

p = 0

Ф _p ( i , j )    Ф ,, . )                   ----

-— ^ min, i , j = 1, N . (17)

2cP J

V

где ф , е [ 0,2 nK ], j = 0, N , c 0 = 1.

профиля равны

( d 1 ,..., d 8 ) = ^L5^? ( 0,1,3,4,5,7,8,8 ) мкм .     (14)

⁽ n 0 ^- 1 )

Согласно результатам расчета интенсивностей ± 1 порядков (13), решетка (14) направляет 100% энергии спектральной компоненты 1 ₀=1,55 мкм в 0-й порядок и по 87,5% энергии спектральных компонент 1 + 1 в порядки 1-й и -1-й. Полученная решетка, по сравнению с аналитически рассчитанной решеткой (2), теряет 12,5% энергии для спектральных компонент 1 ± 1 , однако имеет в 2,5 раза меньшую высоту и более простую структуру периода. Приведенный пример показывает, что при N>8,9 для снижения технологических требований решетки для разделения длин волн (1) также следует рассчитывать из условия минимума невязок (11).

Приведенный подход легко обобщается на случай разделения более трех длин волн. При этом для