Расчет спектров волн экранированных волноводов с произвольным диэлектрическим заполнением с помощью модифицированного метода Галеркина и метода частичных областей

Широкое использование в технике СВЧ- и КВЧ-волноводов со сложным диэлектрическим заполнением обуславливает высокую актуальность разработки методов их строгого электродинамического расчета. Основными методами, используемыми на данный момент, являются метод частичных областей (МЧО) и разнообразные вариации сеточных подходов (метод моментов, метод конечных разностей и т. д.).

В работе рассматривается метод расчета спектров собственных волн круглых и прямоугольных экранированных волноводов с произвольным диэлектрическим заполнением, являющийся модификацией метода Галеркина (ММГ) и основанный на представлении полей волн направляющей структуры в виде разложения по собственным функциям краевой задачи для однородно заполненных волноводов [1; 2].

1. Расчет экранированного круглого волновода с градиентным диэлектрическим заполнением

Рассмотрим задачу о распространении Е- и Н-волн в круглом экранированном волноводе с частичным диэлектрическим заполнением, значение диэлектрической проницаемости которого произвольным образом зависит от радиальной координаты ( б ( r , ф , z ) =б ( r ) ) (рис. 1). Значение

магнитной проницаемости полагается величиной постоянной.

Из уравнений Максвелла получаем известное соотношение rotrot E = k 0 б ( r , ф ) E , которое в цилиндрической системе координат выглядит как:

rot rot

(E )| = 1    + дE г r дr дф д r д z

₊ 1 ^{д E} ф   д ² E r

⁺ r ^{2 д} ф   д z ²

1 д ² E r 2^2

r дф

= ^k 0 б ( r , ф ) E r ;

l ^      1      1 д2 E    1 дE rot rot (E) = —Em +--r- —- —r ф r 2 ф r дr дф r 2 дф

1 д ² E z S^{2 E} ф 1 ^{д E} ф ^д 2 ^E ф — r дфд z д r ² r д r д z ²

rotrot ( E i )|

I = ^д 2 ^E r ' z д r д z

+

= k 0 ^б( r , ф ) E ф ;

₊ 1 ^{д E} r ₊ 1 ^д 2 ^E ф r д z r дфд z

д ² E z 1 д E z 1 д ² E z — д r ^{2 r д r} r ² дф ²

= k 0 ^б( r , ф ) ^E z .

Поля волн направляющей структуры представляем в виде разложений по собственным функциям краевой задачи для однородно заполненного круглого волновода.

Рассматривая симметричные Н-волны, полагаем д / дф = 0, E r = 0, E z = 0. В этом случае уравнения (1) сведутся к единственному уравнению относительно ф -компоненты электрического поля:

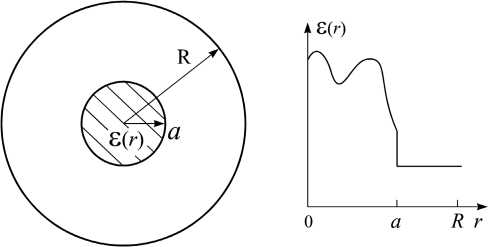
Рис. 1. Профиль диэлектрической проницаемости

Fig. 1. Dielectric capacitivity profile

R               , n        fr„

J ^rJ 1 ( ^a n r ) ^J 1 ( ^a q r ) dr ^-L

0                                 I^u,

где Г q - 0,5 R ² J 2 ( a n R ) .

q - n ;

q ^ n ,

Уравнение (5) можно представить в матричном виде:

I • b - T • b                                                      (6)

где

I q , n

1 „    ^д 2 E ? 1 ^д E ? 8 ² E ?

--E------- r2 ?   dr2    r 8 r    дz1

_-.(a 2      ) ^Г q ■

0, q ^ n ,

q - n ;

= ^k 2 ⁸ ( ^r ) E ? .

Записывая E ? ( r , ? , z ) = E ? ( r , ? ) e ‘ ^p z , получаем уравнение относительно функции поперечных ко-

R

T q , n ^{- k} 0 J ^e ( r ) ^rJ 1 ( ^a n r ) ^J 1 ( ^a q r ) dr .

ординат:

> 1 £’7 E H*•( r ^) E .- 0.

Решение уравнения (2) будем искать в виде

E.( r )-'Nbn J1 (anr), n-0

где коэффициенты a _n определяются из уравнения J 1 ( a _nR ) - 0 (т. к. E ? ( R ) - 0).

Подставив (3) в (2), получаем:

N

-' b n-0

^{5 2} J 1 ( ^a n r ), 1 ⁵ J 1 ( ^a n r ) 1

r ~    7 J * ^(a n r

NN

^- ' b n ^k 2 ⁸ ( r ) ^J 1 ( ^a n ^r ) - ' ^b n P ^{2 J} 1 ( ^a n ^r ) .

n - 0                     n - 0

Учитывая, что d2J1 (anr) + 1 5J1 (anr) _ дr2       r    д r

^_ 4 ^J 1 ( ^a n r ) ^-_a n J 1 ( ^a n r ) , r

получаем:

NN

' ^b n ( ^a n +P ² ) J 1 ( ^a n ^r ) ^- ' b n ^k 0 ⁸ ( ^r ) ^J 1 ( ^a n ^r ) .       ⁽⁴⁾

n - 0                         n - 0

Умножив обе части уравнения (4) на rJ 1 ( a ^ r ) и проинтегрировав в пределах r g Q 0; R ] , выводим уравнение

Записав уравнение (6) в виде ( I - T ) • b - 0 и приравняв определитель матрицы ( I - T ) к нулю, получаем дисперсионное уравнение для симметричных Н-волн, распространяющихся в круглом волноводе с произвольной зависимостью 8 от r : Det ( р ) - | I - T | - 0.                                     (7)

Отметим, что матрица T не зависит от в , поэтому при решении дисперсионного уравнения (7) она вычисляется лишь один раз, что существенно сокращает время поиска корней дисперсионного уравнения (ДУ). Заметим, что при выводе уравнений (6), (7) никаких ограничений на вид зависимости 8 ( r ) не накладывалось, т. е. данный метод позволяет рассчитывать симметричные Н-волны при совершенно произвольном характере изменения диэлектрической проницаемости по поперечной координате, при этом 8 может быть и комплексной величиной, что позволяет, например, рассчитывать волноводы со сложным распределением поглощения в поперечном сечении.

В случае симметричных Е-волн полагаем д / д? - 0, E ? - 0. При этом уравнения (1) перейдут в систему двух уравнений:

i P^ E z -+ ( ^k 2 ⁸ ( r ) ^_ Р ² ) E r ^{- 0} ;

ip^r+ip1 Er +^E-+1 dEz+k02 8( r) E - 0, д r      r       д r2    r д r которые, введя обозначение E?z - ipEz, переписываем:

N ^R

( ^{a 2} +Р 2 ) ^Г q b q ^- ' b n ^k 2 J ⁸ ( r ) r^J 1 ( ^a n r ) J 1 ( ^a q r ) dr .    ⁽⁵⁾

n - 0     0

Здесь использовалось условие ортогональности функций Бесселя:

l*V д Ez

- +

д r д 2 Ez д r 2

( ^k 0 ² 8 ( r ) _p ² ) E r - ⁰

1 д Ii_{7 7} о / \ ~       2i д E„ 1      ]

^{+     - + k} 2 ⁸ ( ^r ) E _z ^_p 2 1 -Tr ⁺- E I ^{- 0}

r д r                       l д r    r     j

Граничные условия на идеально проводящей по-

верхности для тангенциальной и нормальной ком-

понент электрического поля

I        d E

E = 0, n^L = 0

I S        d n s

в

данном случае приводят к уравнениям:

E    = °, z r = a	d ( rE r )	= 0. r = a
	d r

Компоненты электрического поля будем искать в виде

NN

E z = 2 A n J 0 ( a n r ) ,    E r = 2 B m J 1 ( a m r )         (1°)

n = 0                     m = 0

С учетом (9) коэффициенты a _n находим из уравнения J 0 ( a _n R ) = 0.

Подставив (10) в (8), получаем систему функциональных уравнений:

NN

• -2 An a nJ 1 (a nr )+2 Bm ( k2 e(r)-e2 ) J1 (a mr ) = °; n=0

NAn  ^    +1   '    + kЫr)J0(anr)]-

• ■         ar rd

n=0    v    d r7

fdJ (amr) 1 /\

-P 2 2 B m          +- J 1 ( a m r ) = °.

I      d rr m=0   v7

С учетом равенств

^{d 2} J 0 ( ^a n ^r ) + 1 ⁵ J 0 ( ^a n ^r ) d r ^{2        r    d r}

2 n

J 0 ( ^a n ^r ) ;

^{d J} 1 ( ^a m ^r )

d r

= ^a m J 0 ( ^a m ^r ) ^- "^J 1 ( ^a m ^r )

систему (11) можно переписать в виде

N

—2 An a n J1 (a n r ) + n=0

N

+ 2 B m ( k^{2 £} ( r ) — ^в 2 ) J 1 ( ^a m r ) = °;

m = 0

N

2 An (k28(r)-an)J0 (anr)- n=0

N

-P2 2 BmamJ0 (amr) = °- m=0

NR k0 2 An J r£(r) J0 (anr) J0 (aqr) dr -n=0   0

- A q a 2 ^Г q - B q ₽ 2 a q ^Г q = ° ^-

Систему уравнений (13) можно записать в матричном виде:

" T ( °,° ) T ( 0,1)

T ( 1,° ) T ( 1, ¹ )

= °,                              (14)

где

( 0,0 )           g q, m      a q q q, m,

R Ty = k o J r 8 ( r ) J 1 ( a m r ) J 1 ( a q r ) dr - P 2 Г q 5 q , m , 0 R	(15)
T n ) = k o J r 8 ( r ) J ° ( a n r ) J ° ( a q r ) dr -a 2 Г q 5 q , m ,

T q ^ =^- P ^{2 a} q ^Г q ⁵ q , m ; ⁵ q , n ^{- символ} Кронекера-

Приравнивая определитель системы (14) к нулю, получаем ДУ Е-волн волновода с произвольным радиальным диэлектрическим заполнением.

2. Расчет тестовой структуры

В качестве примера проведем расчет простейшей тестовой структуры – круглого волновода с однородным диэлектрическим стержнем (т. е. e ( r ) = 8 = const, рис. 2) и сравним результаты с полученными классическим методом частичных областей (МЧО) [3; 4].

Расчеты проводились для волновода с параметрами R = 20 мм, a = 10 мм, 8 = 3 на частоте f = 10 ГГц. МЧО дает следующие результаты: для Н-волн в H = 237,68916 м ^{- 1}, для Е-волн В_Р= 227,55000 м ^{- 1}.

E

Предлагаемый метод (ММГ) с использованием функции

Умножая первое уравнение (12) на а второе на rJ 0 ( a q r ) и интегрируя в r g [ °; R ] , выводим систему уравнений:

NR

-AqaqГq + k0 2 Bm J r6(r) J1 (amr)x m=0    0                                (13)

^rJ 1 ( ^a q r ) , пределах

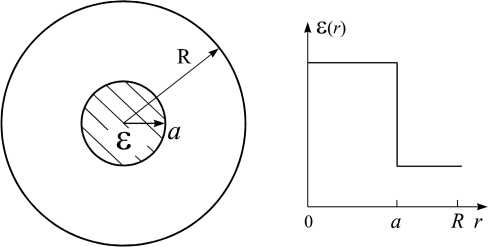
Рис. 2. Тестовая структура круглого волновода с частичным диэлектрическим заполнением

Fig. 2. Test structure of a circular waveguide with partial dielectric filling

^{X J} 1 ( ^a q r ) dr ^- B q P ^{2 Г} q = °;

Таблица 1. Расчет модифицированным методом Галеркина

Table 1. Calculation by the modified Galerkin method

N	Е-волны ( P e = 227,5500 м 1)	Н-волны ( P h = 237,6892 м 1)
1	233,1366	234,7509
2	234,3096	236,5369
3	232,3624	237,2738
4	231,8978	237,4027
5	230,9273	237,5506
6	230,7095	237,5777
7	230,1335	237,6259
8	230,0207	237,6347
9	229,6397	237,655
10	229,5748	237,6586
11	229,304	237,6686
12	229,2637	237,6704
13	229,0613	237,6758
14	229,0347	237,6768
15	228,8776	237,6800

^Б ( r ) =

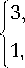
r <  a ;

a <  r <  R

дает результаты, представленные в табл. 1.

Сходимость решений, получаемых модифицированным методом Галеркина для Е и Н-волн, представлена в табл. 1 и на рис. 3.

Из табл. 1 и рис. 3 видно, что сходимость ММГ является монотонной и наступает достаточно быстро (уже при N = 5 разница между продольными волновыми числами не превышает 1,5 %). Из рис. 3 также видно, что в случае Н-волн сходимость наступает быстрее.

На рис. 4 пунктирной линией представлены зависимости компонент поля H z и E ^ от координаты r , рассчитанные для Н-волны при N = 5.

Из рис. 4 следует, что распределения полей, рас- считанные двумя методами, практически совпадают, что подтверждает корректность предлагаемого метода.

• 3.    Расчет волновода с градиентным диэлектрическим заполнением

На основе уравнений (15) проведем расчет дисперсионных характеристик Е-волн круглого волновода с частичным диэлектрическим заполнением параболического профиля:

^б( r ) =

_Р ^Б 1 ^-Б 2_Г2

^Б1-- r , a ²

• 1,    a <  r <  R .

  r <  a ;

  
  

• 4.    Расчет прямоугольных экранированных волноводов с произвольным диэлектрическим заполнением

Результаты расчета дисперсионных характеристик Е-волн круглого волновода с параболическим профилем диэлектрического заполнения представлены на рис. 5. На рис. 6 приведены распределения вектора Умова - Пойнтинга по поперечному сечению волновода, рассчитанные для трех мод на частоте f = 14 ГГц.

Поперечное сечение прямоугольного волновода с диэлектрическим заполнением, регулярным по продольной координате z и произвольным по поперечным, изображено на рис. 7. Значения диэлектрических проницаемостей могут быть и комплексными величинами.

Представив диэлектрическое заполнение прямоугольного волновода в виде кусочно-непрерывной функции:

Б1 (x, y) на S1, Б2 (x, У) на. S2, Б( x, y ) = < •, Бn (x, У) на sn , б на S±, запишем уравнения Максвелла внутри волновода:

rot ( E ) = - i юц 0 H ; rot ( H ) = i юб ( x , y ) б 0 E .        (16)

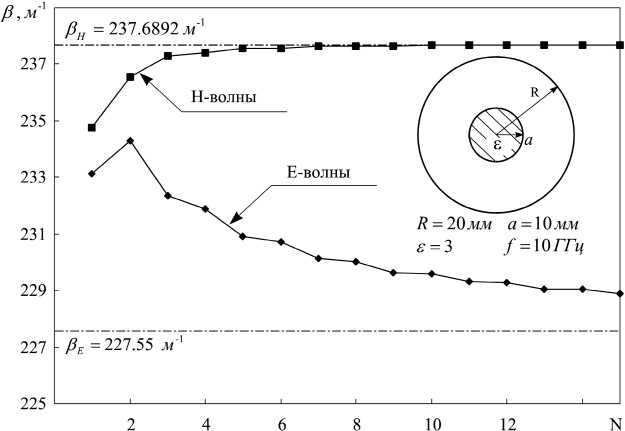
Рис. 3. Сходимость модифицированного ММГ и МЧО

Fig. 3. The convergence of the modified MMG and MChO

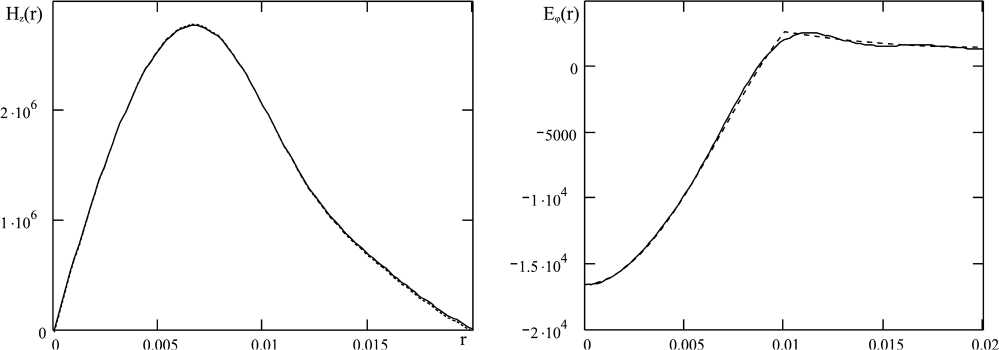
Рис. 4. Распределение поля Н-волны (пунктирная линия – МЧО, сплошная линия – ММГ)

Fig. 4. The distribution of the field of the H-wave (dashed line - MCHO, solid line - MMG)

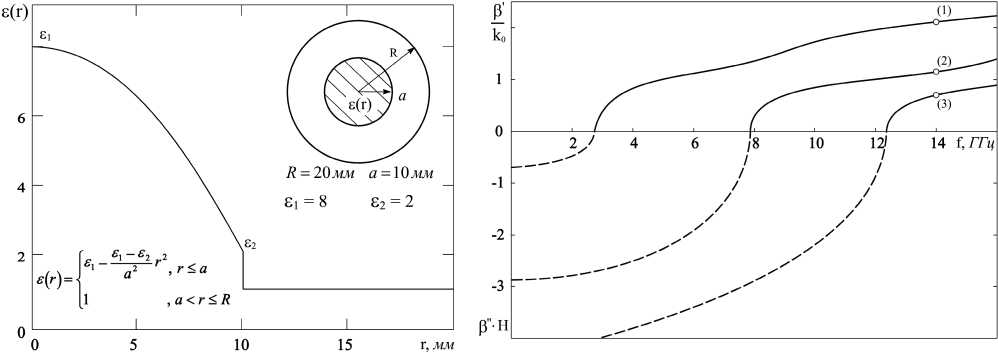
Рис. 5. Дисперсионные характеристики Е-волн круглого волновода с параболическим профилем диэлектрического заполнения

Fig. 5. Dispersion characteristics of E-waves of a circular waveguide with a parabolic dielectric filling profile

Рис. 6. Распределение мощности Е-волны на частоте f = 14 ГГц

Fig. 6. Power distribution of the E-wave at a frequency of f = 14 GHz

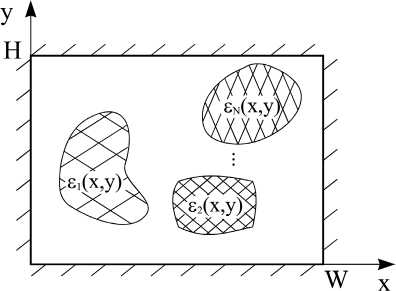
Рис. 7. Общая структура поперечного сечения волновода

Fig. 7. General structure of the waveguide cross section

Подчиняя компоненты (18) граничным усло-

виям:

E z

E z

I x = 0 = ⁰ I y = 0 = 0,

E x l y = 0

= 0,

E x l y = H

= 0,

E = 0, ^y x = 0

E z

E z

I x = W = 0,

I y = H

= 0;

^d E x d x

= 0, x = 0

^d E x d x

= 0,

X = W

^d E y 5 y

= 0, y = 0

Из уравнений (16) получаем:

rot rot E = k 2 8 ( x , y ) E ? ;

^ 2 5 ^ + ( k 02 8( x , y )-p2) Ex -^ E + i p^ E ^ = 0; a y 0 ( 0 ( ,? ) p ) x d x d y p d x

d 0 Ey - + ( k 0 8 ( x , y H0 ) E, -d E + if^lz = 0;     (17) d x 0                     y d x d y     d y

d 0 E,  d 0 E                  d Ev     d Ey

2z +    Z + k 0 8 ( x , y ) E + l p   x + l p/= 0. d x 0     d y 0                    d x      d y

Зависимость компонент электрического поля E_x , E_y , E_z от поперечных координат будем искать в виде

^{E y} l x = W

= 0,

d E y 5 y

= 0

y = H

и заменяя

бесконечный предел суммирования

конечным числом М, выражения (18) приводим к

Ex=2 2 ( ap sin (n px)+Ap cos (npx))x p=0r=0

^X ( a r sin ( d r y ) + a r cos ( d r y ) ) ; to to

Ey=2 2( bp sin (§ px)+Bp cos(§ px))X p=0 r=0                                               (18)

^X ( b r sin ( x r y ) + b r cos ( x r y ) ) ;

Ez = 2 2(CP sin (кpX) + CP cos (кpX)) X p=0r=0

^X ( c r ^sin ( ° r У ) ⁺ c r ^cos ( ° r y ) ) .

виду

MM

E x = 22 a p , r ^cos ( n p^x ) ^sin ( ^d - у ) ;

p = 0 r = 0

MM

E y = 22 b p ,- ^sin ( ⁸ p x ) ^cos ( x r y ) ;                 ⁽²⁰⁾

p = 0 r = 0

MM

^E z = 22 c p , r ^sin ( ^к p ^x ) ^sin ( ° - у ) .

p = 0 r = 0

Здесь n =np;    d =n(r+l);    . =n( P+1);

pH r H      p W nr n( P +1)          n( r + 1)

Xr = —;   кп = —-----; ° = —----;

r H p W       r H

p = 0,1, _ , M ; r = 0,1, _ , M .

В этом случае члены сумм (20) являются решениями краевой задачи для однородно заполненного прямоугольного волновода с граничными условиями (19).

Запишем выражения (20) как v N           (x)         (x)

E x = E a n cos I ^a П ^x I sin I У П k I , n = 0

E y = E b m sin f ^am) x I cos G in ) У ] m = 0

p N           ( z )          ( z )

E„ = c sin a x sin y У , z tt    t t=0       v У v У

N q ,

HW

JJ

0 0

(z)           HW x sin I yq ’y I dxdy = 5q,n -4-;

где нии

N = ( M + 1)² - 1. При одиночном суммирова-(21) учитывается весь спектр функций в (20).

Коэффициенты a nx , ^y , z ) и y nx , ^y , z ) записываются следующем виде:

в

a ⁽ x )                   ⁽ x )    . = 9     J y )

^a p + ( M + 1) r ⁿ p ,     ^y p + ( M + 1) r ⁹ r , ^a p + ( M + 1) r ⁵ p ,

( y )         _           ( z )         _ L ( z )

Y p+(M+1) r = X r,   a p+(M+1) r = kp, Y p+(M+1) r = G r, где p = 0, 1, …, М; r = 0, 1, …, М. Например, при М = 2

( x )       ( x )

a и y запишутся в виде

„ (x)                                         T a "(По, П1, П2, По, П1, П2, По, П1, П2 ) ,

Y ⁽ x ) = ( Э 0 , Э о , Э о , 9 1 , 9 1 , 9 1 , 9 2 , 9 2 , 9 2 ) T .

Таким образом, решение задачи о расчете волноводов с произвольным заполнением сводится к представлению электрического поля в виде (21). Связь между x- , y- , z -составляющими поля в (21) определяется коэффициентами a n , b m , c t , значения которых находятся из системы алгебраических уравнений путем подстановки (21) в (17) и использования условий ортогональности собственных функций краевой задачи для однородно заполненного прямоугольного волновода. Подставив выражения (21) в систему (17), получаем систему функциональных уравнений, которую проецируем на базис собственных функций краевых задач для однородно заполненного прямоугольного волновода.

С учетом обозначений:

HW

где 5 q _n - символ Кронекера, получаем систему матричных уравнений:

xx    x      x

• -I Г N + Р 2 N   I a + k 02 Q a +

• + W ⁽ x ) b + i p V ⁽ x ) c = 0;

4Г ^y ) N ^{( y} ) +p ² N ^{( y} ) ) b + k 2 Q ^{( y} ) a +

^{V                     У}                                   (23)

• + W ^{( y} ) a + i p V ^{( y} ) c = 0;

• -Г ⁽ z ) N ⁽ z ) c + k 0 Q ⁽ z ) c -

• - i p W ⁽ z ) a - i p V ⁽ z ) b = 0,

где

Г ^{( x )}=fy ⁽ x ⁾ ) 2 5      Г^{( y}         y ⁾ ) 2 5

q , n I ^y n I q , n ,       q , n I ^a n I q , n ,

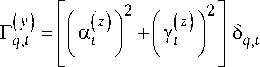
– диагональные матрицы,

HW

Q⁽ x )

q , n

x cos

0 0

HW w (x LJy )A y)       L( yk) | Jy )v]x

W q , m = ^a m ^y m J J ^cos I ^a m ^x I ^sin I ^y m ^y I ^х

0 0

x cos

= a,

N q ,

0 0

x sin

[ ( x )

1, если a П ’ = 0;

( x )

0,5, если a n ⁷ * 0;

HW

N q ,

x

0 0

x cos ^y ( У ) y ) dxdy = 5 q _n

[                ( У )

HW 1 1, если у П ’ = 0;

² 1 о,5, если у П ^У ) * 0;

( x )             ( x )

a q ⁷x I sin I y q ⁷y I dxdy =

WH

( y )      ( x )       ( y )      ( x )

, ^{если a} m -^a q ) ^и y m ) =y q ) ;

⁽ y )A y ) J 4

'm ^Y m In         ( y ), ( x )        ( y )Л x )

1 0, если a m ⁷ * a q ⁷ или y m ⁷ * y q ⁷;

V ⁽ x ) = a¹

^V q , t     ^a|

x cos

( z ) = a _t

HW

0 0

WH           ( z )     ( x )     ( z )    ( x )

——, если a t ⁷ = a q ’ и y t ⁷ = y q ⁷;

( z )       ( x )            ( z )      ( x )

0, если a t ⁷ * a q ’ или y t ⁷ * y q ⁷;

HW

Q qym = j j ^e ( x , y ) sin ( ^am) x у cos ^Ym ) y у

0 0

x sin

p ² W ⁽ z ) a + P ² V ⁽ z ) b +

w ^{( y} ) = J

^W q , n    ^ai

HW

x

+ ^[ k 0 Q ⁽ z ) -Г ⁽ z ) N ⁽ z ^{) ]} c ' = 0.

x sin

Полученную систему можно записать в виде матричного уравнения:

WH

= a.

^V (

( x )      ( У )       ( x )      ( У )

, если a П ⁷ = a q⁷ и у n ⁷ = у q ⁷;

^{( x} H ^x ) J 4

' n Z n |

( x )      ( y )           ( x )      ( y )

1 0, если a n ’ * a q ⁷ или у n ’ * у q ⁷;

a

A- b

где

HW

c ‘

A =

x sin

WH

( z )      ( y )       ( z )      ( У )

, если a t ⁷ = a q и у t ⁷ = у q ;

( z ) T"

= У t 1 4

( z )      ( y )           ( z ) ( y )

1 0, если a t ⁷ * a q или у t ⁷ * у q ,

HW

Q / = JJ

x sin

W ⁽ z ) = ct¹

W q , n   ^ai

HW

x sin

=a

( x )       ( z )        ( x )      ( z )

( x ) I T , ^{если a} n = ^a q ^и у n =^Y^; ; n L             ( x )     ( z )          ( x )     ( z )

1 0, если a n ’ * a q ’ или у n ’ * у q ⁷;

WH

HW v (z )_J y)      [JyL] Цy ku

^V q , m = ^y m J J ^sin I ^a m ^x I ^sin I ^y m ^y \ ^x

x sin

= Y

wh           ( y )     ( z )     ( y )    ( z )

(y) I ~, если am! = aq' и ym = Уq7, m L            (y)     (z)          (y) (z)

1 0, если a m ⁷ * a q ’ или у m ⁷ * у q ⁷.

Введя переменную c ‘ = i p c , систему уравнений (23) преобразуем в:

^[ k 2 Q ⁽ x ) —Г ⁽ x ) N ⁽ x ) -P ² N ⁽ x ^{) ]} a + + W ⁽ x ) b + V ⁽ x ) c ' = 0,

W ^{( y} ) a + ^[ k ² Q ^{( y} ) - Г ^{( y} ) N ^{( y} ) -p ² N ^{( y} )^] b + + V ^{( y} ) c ‘ = 0,

= 0,

k 0 Q ⁽ x ) —Г ⁽ x ) N ⁽ x ) -p ² N ⁽ x )

W ( ^y )

P ² W ⁽ z )

W ⁽ x )

V ⁽ x )

k ₀ ² Q ^{( y} ) -Г ^{( y} ) N ^{( y} ) -p ² N ^{( y} )          V ^{( y} )

P ² V ⁽ z )               k 0 Q ⁽ z ) -Г ⁽ z ) N ⁽ z )

Приравнивая определитель матрицы A к нулю, получаем ДУ волн прямоугольного волновода с

произвольным диэлектрическим заполнением.

Отметим ряд особенностей предложенного ме-

тода. Из формул (24)–(26) видно, что от функции

диэлектрического заполнения б

только матрицы

Q ⁽ x ) ,

Q ^{( y} ) и Q ⁽ z )

( x , y ) зависят

, которые при

этом не зависят ни от частоты, ни от значения продольного волнового числа р . Таким образом, все матрицы, входящие в (28), для сколь угодно сложной структуры считаются лишь единожды, а затем просто домножаются на к 2 и р ². Это позволяет существенно сократить время расчета дисперсионных характеристик.

5. Прямоугольный волновод с угловым диэлектрическим заполнением

Рассмотрим тестовую задачу, позволяющую провести сравнение предложенного метода с использующим аппарат LM- и LE -волн [5]. Приведем результаты расчета направляющей структуры, представленной на рис. 8.

Параметры структуры: W = 8 мм, w = 5 мм, H = 10 мм, h = 6 мм, б = 6. Расчет данного волновода проводился двумя способами: предложенной модификацией метода Галеркина и методом частичных областей, при котором поперечное сечение волновода разбивалается на области (1) и (2) (рис. 8), поля в которых представляются с привлечением аппарата LM- и LE -волн.

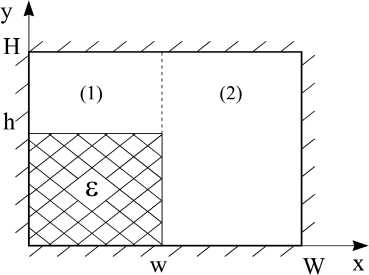
Рис. 8. Прямоугольный волновод с угловым координатным диэлектрическим заполнением

Решения дисперсионного уравнения, полученные в различных приближениях двумя способами, приведены в табл. 2 и на рис. 9.

В табл. 2 представлены результаты решения дисперсионной задачи методом частичных областей (второй столбец) и модифицированным методом Галеркина (третий столбец). Первый столбец - порядок приближения М. Рис. 9 - графическое изображение данных табл. 2.

Из табл. 2 и рис. 9 видно, что оба метода дают сходимость к одному и тому же значению. При этом результаты близки уже на малых приближениях (при M = 5 нормированные постоянные распространения, полученные двумя методами, отличаются лишь на 0,2 %). С помощью МЧО и ММГ были рассчитаны дисперсионные характеристики данного волновода в частотном диапазоне от 2 ГГц до 16 ГГц (рис. 10). Результаты расчетов, получен-

Таблица 2

Table 2

M в/к0 (МЧО) в/k0„ (метод Галеркина) 2 1,755013 1,753340 3 1,754223 1,757953 4 1,754177 1,758168 5 1,754127 1,757674 6 1,754045 1,757714 7 1,754059 1,757299 8 1,754024 1,756771 9 1,754026 1,756791 10 1,754022 1,756399 11 1,754013 1,756185 12 1,754017 1,756157 13 1,754009 1,755862 14 1,754010 1,755804 15 1,754009 1,755589 ные обоими методами, практически полностью совпадают (дисперсионные кривые графически неразличимы).

Как видно из рисунка, в спектре собственных волн волновода присутствуют комплексные волны (КВ), дисперсионные характеристики которых начинаются в точках жордановой кратности волновых чисел.

На частоте 14 ГГц в точках, обозначенных на рис. 10 цифрами (1)–(3), обоими методами были рассчитаны распределения вектора Умова –

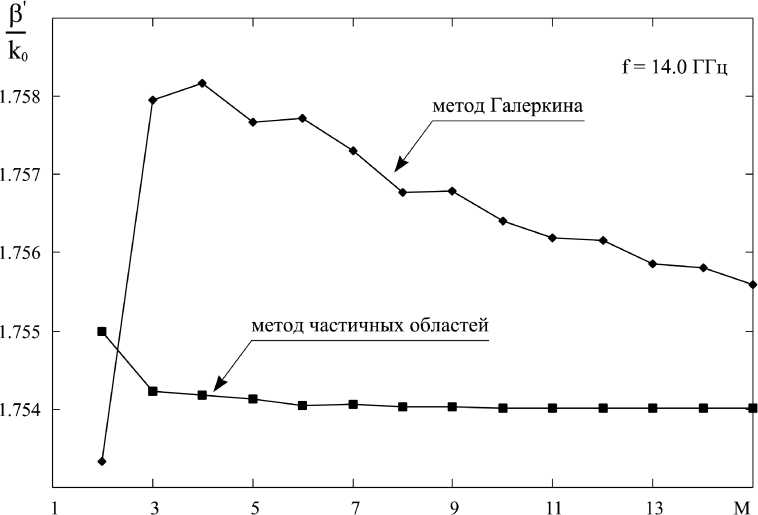
Рис. 9. Сходимость модифицированного метода Галеркина и МЧО

Fig. 9. Convergence of the modified Galerkin method and the MChO

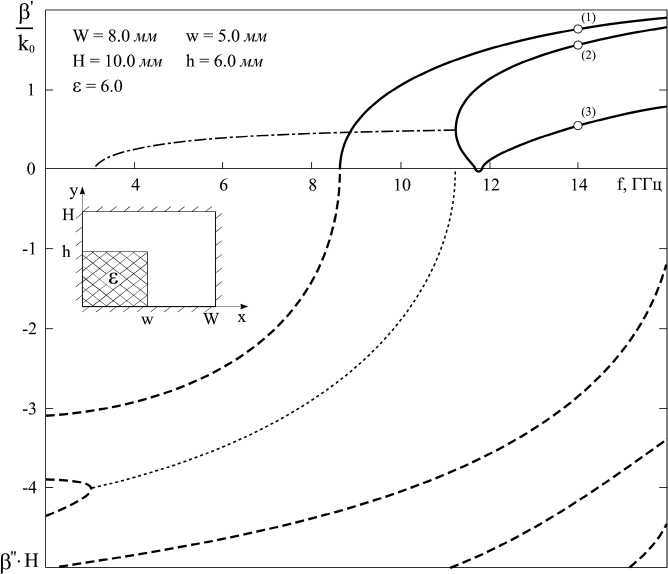
Рис. 10. Дисперсионные характеристики прямоугольного волновода с частичным диэлектрическим заполнением

Fig. 10. Dispersion characteristics of a rectangular waveguide with partial dielectric filling

(1)                                    (2)                                   (3)

а – модифицированный метод Галеркина

(1)                                    (2)                                   (3)

б – метод частичных областей (с использованием аппарата LM и LE-волн)

Рис. 11. Поток мощности в прямоугольном волноводе с угловым координатным диэлектрическим заполнением: заполнением ( а – предложенный метод; б – МЧО)

Fig. 11. Power flow in a rectangular waveguide with an angular coordinate dielectric filling: filling ( a – the proposed method; b – MChO)

Пойнтинга по поперечному сечению волновода. Световое представление распределения плотности потока мощности приведено на рис. 11.

Таким образом, на примере прямоугольного волновода с частичным диэлектрическим заполнением показана двойственность предложенного метода.

Заключение

• 1.    Предлагаемый метод расчета волноводов, неоднородно заполненных диэлектриком, является универсальным: единственное ограничение – внешняя металлизированная граница должна быть координатной. При этом легко формулируется краевая задача для соответствующего однородно заполненного волновода (волновода сравнения), и определяется базис представления полей.

• 2.    Метод обладает преимуществом по сравнению с МЧО при решении задач подобного класса, так как не требует введения в частичных областях, для которых нельзя сформулировать краевую за-

• дачу Штурма – Лиувилля, непрерывного спектра собственных функций.

• 3.    Метод прост в алгебраизации дисперсионных задач и среди множества компьютерных методов представляется наиболее строгим и математически обоснованным.

• 4.    Составлен алгоритм расчета характеристик симметричных волн цилиндрического волновода с осесимметричным диэлектрическим заполнением, имеющим произвольную зависимость б ( r ) . Метод, являющийся модификацией метода Галеркина, не требует аналитического представления поля.

• 5.    Сравнением результатов решений тестовых задач подтверждены корректность и действенность предложенного метода.

• 6.    Метод является альтернативным по отношению к МЧО в тех случаях, когда последний требует многослойной аппроксимации диэлектрического заполнения, и может быть распространен на все волноводы с координатными экранирующими поверхностями.