Расчет теплового режима электрического генератора микрогазотурбинной установки

Во время работы электрического генератора микрогазотурбинной установки в его статоре и роторе выделяется значительное количество тепла, поэтому для обеспечения допустимого уровня температур необходимо осуществить эффективное охлаждение генератора. Отвод тепла от статора осуществляется воздухом, протекающим по каналам прямоугольного сечения на внешней поверхности статора. Охлаждение ротора выполняется воздухом, протекающим в кольцевом зазоре (рис. 1).

Рис. 1. Расчетная схема генератора: 1 – ротор; 2 – защитное кольцо;

3 – воздушный кольцевой зазор; 4 – статор; 5 – ребра; 6 – воздушный канал статора

Каналы статора 6 выполнены фрезерованием в кольце из алюминиевого сплава, напрессованного на статор. В результате каналы разделяются продольными ребрами 5 трапециевидного сечения. Статор представляет собой пакет из тонких стальных пластин, между которыми практически отсутствует тепловой контакт, поэтому предполагается, что теплота, выделяющаяся в них, к охлаждающему воздуху передается только в радиальном направлении. Теплообменом с торцевых поверхностей статора и ротора можно пренебречь, поскольку площадь боковой поверхности значительно больше торцевых. При этих условиях температурное поле в статоре и роторе можно считать одномерным, в котором температура изменяется только в радиальном направлении. Предполагается также, что внутреннее тепловыделение в статоре равномерно распределено по его объему. Распределение температуры в роторе определяется из решения следующей задачи.

d ² t ₁ dr ²

+ 1 dtL + q = о, о <  r <  r ; r dr X ¹

d ² t 1 dt

—2 + "r = 0, R < r < R 2 ; dr ² r dr

dti (0) = 0.

dr

t 1 ^{( R} 1 ) ^— t 2 ^{( R} 1 ) ;

^dt 1 ^{( R} 1 )        dt 2 ⁽ R , ) _

Xi -------- = X 2 -------- ;

dr dr

-X 2 dt 2 ⁽ R ² ) ^{— a} 3 [ t 2 ⁽ R 2 ^{) —} t 3 ] . dr

В (1)–(6) t – температура; r – радиальная координата; q_{v 1} – плотность внутренних источников тепловыделения в роторе; X - коэффициент теплопроводности; а - коэффициент теплоотдачи; индексы: 1 – металл ротора; 2 – защитное кольцо; 3 – кольцевой канал.

Решение системы (1)–(6) имеет следующий вид t1 (r ) — 1 3 +

¹ 2 ⁽ r ^{) — 1} 3 +

q v i R lt ln R 2 + I v L ( r ²

2 X ₂     R 1    4 X 1 ^{v 1}

q v 1 R 1² _ln R x ₊ q v 1 R 1²

2 X ₂ r   2 R ₂ а ₃

^^^^^^^B

r ² ) + q v ^{1 R} 1 , 0 <  r <  R ;

' 2 R ₂ а ₃            ¹

, R 1 <  r <  R 2 .

Температура на поверхности защитного кольца есть

1 2 ( R 2 ) = 1 3 + q/

2 R ₂ а ₃

.

Рассмотрим задачу о распределении температуры в статоре с внутренним тепловыделением. Расчетная схема статора приведена на рис. 2.

d ² t    1 dt    q

• —f ⁺    “ ⁺ T" ^{— 0}, ^R 3 <  r <  ^R 4 ;

dr    r dr X c tc(R 3)— t 4;

• ¹ c ^{( R} 4 ) ^{— 1} 5 .

Решение задачи (10) – (12) имеет вид

¹ c ⁽ r ^{) — 1} 4

^^^^^^^B

qv^L2__R2\ l^{n (} r/R 3 ) г _

4 X _c ( r R ^{3 )+} ln ( R 4,/ R 3 )[ t ⁵ t ^{4 +}

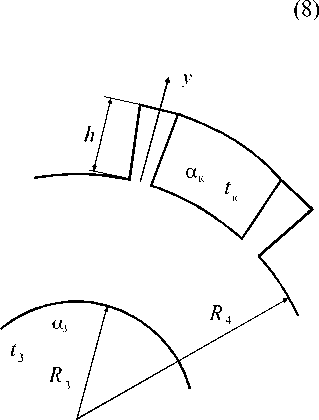
Рис. 2. Схема статора

+ q vc^ ( R ₄ ²

4 X _c ^{V 4}

Здесь t ₄ ,

^^^^^^^B

t ₅ – температуры на внутренней и наружной поверхностях статора соответственно.

Плотность теплового потока на радиусе r есть

dt q ——x c - = dr

q v c r

^^^^^^B

— ln R - L

X c    R 3

t ₅

^^^^^^B

1 ₄ + —

⁴ 4 X _c

^^^^^^B

В (10)-(14) qvc - плотность внутреннего тепловыделения в статоре; X c - коэффициент теп- лопроводности статора; q – плотность теплового потока.

Количество тепла, которое проходит через внутреннюю поверхность статора длиной l, есть а3 (t4 — 13 )2пR31 — qvcпR321---------— 15 — 14 + ^vc (R,2 — R32) .

J-ln R 4 L       ^{4 X} c         J

2 X _c R ₃

Количество тепла, проходящее через наружную поверхность длиной l , есть

Q 4 — qv c п R 4 1 — /l     1 5 — 1 4 + qv^- ( R 4 — R 3) .

Xln R 4 L       ^{4 X} c        J

2 X c R 3

Это количество тепла передается воздуху через стенку с ребрами

Q 4 ^{— а} к f св ^{( 1} 5 ^{— 1} к ⁾⁺ q р f, N р .

Расчет и конструирование

Здесь а к - коэффициент теплоотдачи в каналах статора; fсв - площадь наружной поверхности статора, свободной от ребер; qр – плотность теплового потока у основания ребра; fр – пло- щадь основания ребра; Nр – количество ребер.

Длина боковой поверхности ребра отличается от его высоты на 0,2 %, поэтому площадь боковой поверхности ребра трапециевидного сечения отличается от площади боковой поверхности прямого ребра на эту же величину. Учитывая высокий коэффициент теплопроводности алюминиевого сплава, можно с достаточно высокой точностью заменить трапециевидное ребро прямым. В этом случае [1]

q р = ^{( 1} 5 ^- t к 7° к^u р ³ р f , th ( mh ) , ⁽1 8)

где u _р

= 2 ⁽ a + 1 ) ; f , = al ; m =

1/2

u

l3 р fр J

и

Q 4 = ( t 5 ^- t к ) [ N р 7 ^а к u р ³ p f р th ( mh ) ^{+ а} к f св ^] .

Приравниваем (16) и (19).

q v c ^{n R} 2 ^{1 -}

П1

i , r₄¹ --In— L 2 X c R 3

t ₅

-

q_{v c}

4 3 _c

^{- R} 3 ) = ( t 5 ^- t к ) L N р 7 ^а к u р ³ р f p ^th ( mh ) ^{+ а} к f св ^] .

Выразим t5 из (15), подставим в (20) и найдем температуру на внутренней поверхности ста- тора t4 .

t 5 = B i 1 4 + B 2 ,

B 1

= 1 - R ⁰ ln R ⁴;

3 c R 3

q c RMn R ⁴ - -q c - ( R ²

2 3 _c R ₃ 4 3 _c ^{V 4}

-

R 3 ²

^{+ 1} 3

R Xn R 4 .

3 c R 3

¹ 4 =

q_V c n R 4 1 - B 2 A 2 - A 2 q ( R 4 - R 3² ) + A i 1 к ^{4 3} c

⁽ A i ⁺ A 2 ) B i ^- A 2

где A i = N р 7 ^а к u р ³ р f ,^{th (} mh ^)+а к f св ;

. П 1

² = i     R₄

ln ⁴

2 3 c    R 3

.

Температура воздуха по длине кольцевого зазора определяется из решения уравнения dl 3 _ а ₃ ( 1 ₄ - 1 ₃ ) 2 n R ₃ + а ₃ ( 1 5 - 1 ₃ ) 2 n R ₄

dx

G 3 c p 3

Температура воздуха в каналах статора определяется из решения уравнения ^d1 к = A i ^{( 1} 5 ^{- 1} к ) ^.

к p к

Здесь G – массовый расход; c p – удельная теплоемкость. Значения коэффициента теплоотдачи в каналах статора определяются по данным [1], а в кольцевом канале – по данным работы [2].

Изменение давления в кольцевом канале и каналах статора определяется из решения уравнений dEl =__i____ (_G^ d13 +Z 3 GX J ;

dx            G ₃ ² l S ₃ p ₃ T₃ dx     8 S ₃ ² p ₃ ^J

S 3

S 3 ^p 3 P 3

dp K =ⁱ-----f ^G к² d ¹ ^ + Z ^G ^^{2 n}^ dx „     G 2 l S к Р к T k dx ^^k 8 S X ^J

S к S r Рк P k ккк

В уравнениях (25), (26) S – площадь сечения канала; П – периметр канала; ρ – плотность; p – давление; T – абсолютная температура; ζ – коэффициент гидравлического сопротивления.

Значения коэффициента гидравлического сопротивления в каналах статора определяются по

данным [3], а в кольцевом канале – по данным [2].

Расчет теплового режима работы выпол-

нен при следующих исходных данных, полученных в результате электрического расчета: q_vc = 0,977 · 10⁶ Вт/м³; q_{v 1} = 0,812 · 10⁵ Вт/м³. Температура воздуха на входе в генератор 20 °С. Перепад давления в каналах генератора варьировался от 50 до 800 Па. Результаты расчетов приведены в табл. 1 и 2. В табл. 1 приведены значения расходов в кольцевом

Таблица 1

Значения расходов воздуха в каналах генератора

Δp, Па	G к , кг/с	G 3 , кг/с
50	0,2265	0,0002
100	0,3366	0,00041
200	0,50	0,00082
400	0,743	0,00164
800	1,104	0,00329

канале и каналах статора при различных значениях перепада давления в каналах генератора.

В табл. 2 приведены изменения температур в статоре, роторе и воздуха в каналах.

Таблица 2

Значения температуры в элементах генератора, °С

Δp, Па	Ось ротора по длине	Статор по длине	Воздух в кольцевом канале по длине	Воздух в каналах статора по длине	Воздух на выходе из генератора
50	39–386	331–330	20–372	20–64	68
100	39–302	240–245	20–287	20–52	52
200	39–241	178–184	20–226	20–42	42
400	39–193	134–140	20–189	20–35	35
800	39–146	103–109	20–129	20–30	30

Как следует из результатов расчета, средняя по толщине статора температура по длине генератора изменяется незначительно. Значительно сильнее изменяется температура ротора и воздуха в кольцевом канале. Удовлетворительные уровни температур получаются при перепаде давления порядка 800 Па.

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках комплексного проекта «Создание производства модельного ряда микротурбинных энергоустановок нового поколения» по договору № 02.G25.31.0078 от 23.05.2013 г. между Министерством образования и науки Российской Федерации и Открытым акционерным обществом специальным конструкторским бюро «Турбина» в кооперации с головным исполнителем НИОКТР – Федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет).