Расчет упругих характеристик измерительных диафрагм датчиков давления

Схема мембранного прибора, воплощенная в конструкции датчиков разности давлений типа Сапфир22/Метран22 [1], показана на рис. 1, а. В приборе установлены две мембраны, соединенные штоком. Разность давлений в надмембранных полостях датчика Ад приводит к смещению штока, которое регистрируется тензопреобразователем. Пространство под мембранами заполнено жидкостью. Благодаря такому техническому решению, датчик выдерживает двустороннее давление q на 2... 3 порядка превышающее измеряемую величину Ад.

Одна из основных задач, которая решается при проектировании датчика, - сделать его упругую характеристику (зависимость между измеряемой величиной и перемещением чувствительного элемента) возможно более близкой к линейной. Очевидно, чем меньше нелинейность, тем проще и дешевле регистрирующая электронная часть датчика, обрабатывающая сигнал тензопреобразователя. Актуальность получения упругой характеристики прибора расчетным путем с этой точки зрения очевидна. Существует и другая причина интереса к проблеме численного моделирования поведения мембран. Метрологические параметры приборов, в частности нелинейность упругой характеристики, существенным образом зависят от производственных факторов. В результате неблагоприятного их сочетания у части приборов нелинейность превышает допустимый уровень (для датчиков Сапфир22/Метран22 - 1...2%), и такие изделия приходится браковать.

Рис. 1. Схема двухмембранного датчика и геометрические размеры гофрированной мембраны

Результаты расчетного анализа влияния технологических несовершенств на упругую характеристику приборов помогли бы обнаружить и устранить причины систематических погрешностей и, тем самым, повысить долю качественной продукции. И, наконец, еще одно обстоятельство. Класс точности прибора в конечном счете определяется вариацией его показаний при прямом и обратном нагружениях (допустимая вариация для датчиков Сапфир22/Метран22 составляет 0,1...0,3%). Причины вариации в настоящее время исследованы очень мало, но замечена некоторая корреляция ее с характером и уровнем нелинейности. Таким образом, есть надежда, что ис-

Бурцев С.А., Волошина И.А., Ильина Е.В.,         Расчет упругих характеристик измерительныхМахнович С.В., Русаков И.В. диафрагм датчиков давления следование аномалий упругих характеристик приборов приблизит нас к пониманию природы вариации.

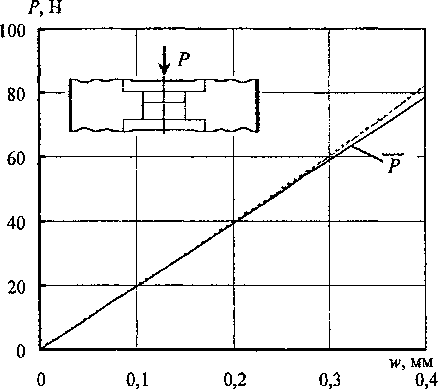
С точки зрения строительной механики оболочек задача, казалось бы, проста: имея под рукой пакет конечно-элементного анализа типа NASTRAN, COSMOS или ANSIS, достаточно только надлежащим образом представить исходные данные (геометрию мембраны, свойства материала, граничные условия, способ нагружения) и получить упругую характеристику прибора. Сложности проявляются с неожиданной стороны: погрешность метода расчета оказывается больше значения искомой величины, то есть степени нелинейности упругой характеристики датчика. Эту ситуацию иллюстрирует пример, приведенный на рис. 2. Здесь показаны упругие характеристики одной мембраны (геометрия мембраны - на рис. 16) при прямом Р„р и обратном Р_обр нагружении силой, приложенной к жесткому центру. Результаты получены с помощью программ NASTRAN и НДС (численное интегрирование разрешающих уравнений теории оболочек с промежуточной ортогонализацией [2]). На этом же рисунке приведены графики изменения величин, характеризующих нелинейное поведение мембраны:

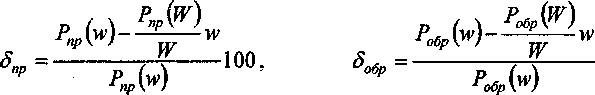
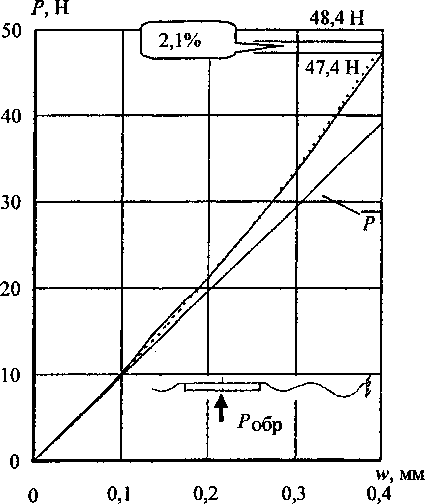
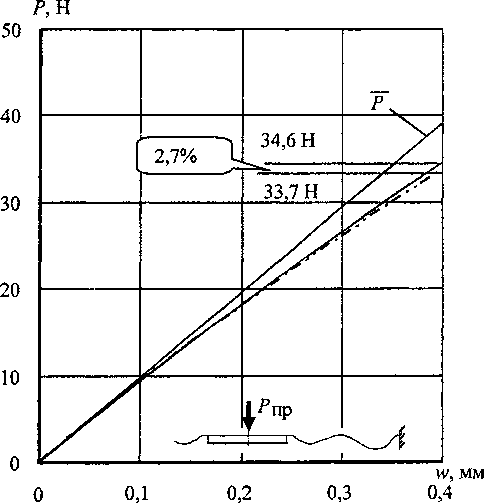
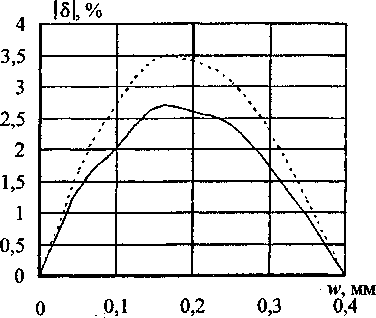
Рис. 2. Упругие характеристики мембраны при прямом и обратном нагружении силой через жёсткий центр: — NASTRAN; — НДС

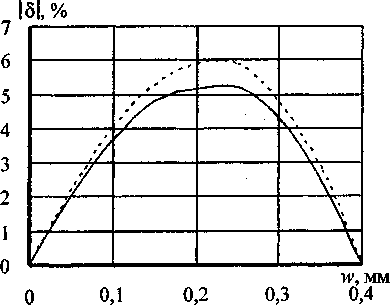
Здесь W- максимальное значение перемещения w. Величина ^достигает наибольшего значе ния 3%, а 5обр - 5,5%. Нелинейность независимо работающей мембраны превышает ожидаемый уровень нелинейности всего датчика (указанные выше 1...2%), но этот факт не является неожиданным - можно предположить, что при совместной работе мембран в блоке их нелинейности будут компенсироваться (кривизны упругих характеристик мембраны при прямом и обратном нагружении имеют разные знаки - см. рис.2). Обратим внимание на то обстоятельство, что расхождение между результатами, полученными по программам NASTRAN и НДС (около 1%), сопоставимо с ожидаемым уровнем нелинейности датчика.

Можно ли, в виду столь больших разбросов по сравнению с уравнением нелинейности, рассчитывать на достаточно удовлетворительное моделирование датчика? Универсальный рецепт нам пока неизвестен. Во всяком случае, очевидно, следует с крайней осторожностью относиться к результатам, полученным одним методом. Всегда желательна перекрестная проверка другими методами. Ясно также, что окончательным выводам должны предшествовать исследование оптимальности конечно-элементной сетки и анализ сходимости решения нелинейной задачи.

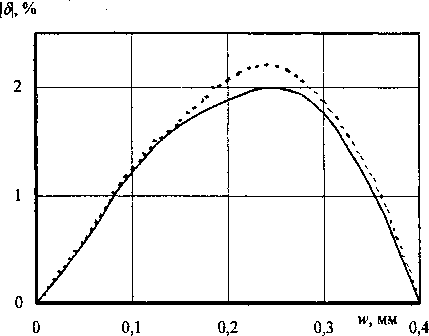
Рис. 3. Упругая характеристика блока мембран: —NASTRAN; —НДС

Покажем далее, что для датчика двухмембранной схемы погрешность используемых в статье расчетных средств не является препятствием к достаточно точному моделированию его упругой характеристики. Приложим к соединенным в блок мембранам силу в центре. Нагружение силой -ситуация для прибора не штатная, но простая для анализа и легко воспроизводимая экспериментально. Нелинейность характеристики блока мембран, и это видно из рис. 3, уменьшается до 2%, а различие между результатами NASTRAN и НДС оказывается всего 0,2%. Блок мембран, как видим, оказывается механизмом, компенсирующим не только нелинейности отдельных мембран, но также и погрешности метода расчета.

Поясним теперь результат с помощью формул. Представим характеристику одиночной мем- браны в виде линейного решения Р = К w (касательная к упругой характеристике в начале координат) и нелинейной компоненты AP(w); тогда для случаев прямого и, соответственно, обратного нагружения имеем: рпр (w) = X ■ w - №пр (w),    Ро6р V^=K-w- ^р (w).

Из условия равновесия штока (жесткостью тензопреобразователя пренебрегаем) находим внешнюю силу:

И^) = ЛарМ+Лн(Ч>

или, после подстановки правых частей выражений (1), P^v) = 2K-w-vf^v\ где /(w) = AP_o6j,(w)-AP_n;,(w).

Нелинейность упругой характеристики совместно работающих мембран

6=    Д —100

с учетом зависимости (3) получает вид

5 =---- W --100.                                                         (4)

Знаменатель в выражении (4), учитывая, что 1KW » f^v\ можно дополнительно упро стить:

5 =------^--юо.

2KW

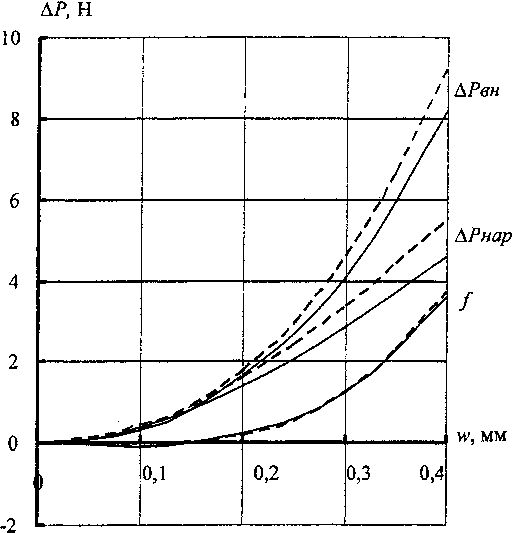
Рис. 4. Нелинейные компоненты упругой характеристики мембраны

Нелинейность характеристики блока мембран, таким образом, определяется разностью малых величин AP„p(w) и A7>o6/)(w); при этом значения /(w), полученные вычислительными средствами NASTRAN и НДС, практически не отличаются (рис.4).

Важным условием, определившим эффект снижения нелинейности в блоке мембран, оказывается малость изменения кривизны упругих характеристик одиночной мембраны в пределах рабочего хода 0,4 мм. При перемещениях, превышающих 0,4 мм, характеристика, соответствующая прямому нагружению, уменьшает свою кривизну и даже меняет знак на обратный (рис. 5). Здесь уже эффект снижения нелинейности оказался бы не столь впечатляющим.

Дополнительный вклад в «линеаризацию» упругой характеристики прибора вносит тензопреобразователь. Этот элемент измерительной системы можно считать линейным звеном. С учетом его жесткости условие равновесия (2) изменится: ^М=д,РМ+д,б;)(>^)+ст -w.

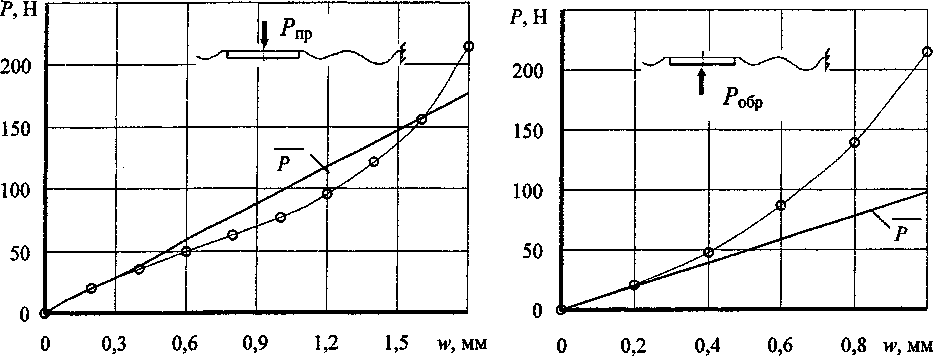
Рис. 5. Изменение характера нелинейности при больших перемещениях центра мембраны

Коэффициент жесткости тензопреобразователя С_т при этом попадает в знаменатель выражения (5):'

’ W (2K + C_m)W ’ - нелинейность датчика оказывается в обратной зависимости от жесткости тензопреобразователя. Для рассмотренных датчиков 2К « С_ТП . Таким образом, максимальное значение 5, а также и различие между решениями в NASTRAN и НДС, уменьшится еще в два раза.

Описанный механизм действует, но несколько более сложным образом, так же и в случае нагружения блока мембран давлением. Моделирование с помощью программы NASTRAN дало следующие результаты: упругая характеристика «сухого» датчика при Ст =0 имела нелинейность 1,1%, а с учетом жесткости тензопреобразователя - 0,2%.