Расчет весенних осадков в горной части бассейна р. Енисей

Постановка проблемы. Основным источником питания рек Сибири являются атмосферные осадки. В холодный период они накапливаются в твердом виде и определяют величину будущего весеннего половодья. Оценка их вклада в весеннем стоке с достаточной точностью определяется с помощью снегомерных съемок в бассейне перед началом таяния. В теплый период осадки выпадают в основном в жидком виде. Количество жидких осадков учитываются сетью метеорологических станций, расположенных, как правило, на равнине. Оценка величины осадков в неисследованной горной части бассейна является одной из задач математического моделировании в гидрологии.

В практике гидрологических расчетов и прогнозов известно несколько способов расчета осадков в бассейнах горных рек. Основное их количество основано на учете достаточно хорошо изученного влияния рельефа местности на образование и распределение осадков. В настоящее время широко применяется метод с использованием плювиометрических градиентов. Например, А.В. Петенков [1] использует следующую линейную схему расчета:

Xi = Xst • 1 + у к

AH Л

100 /

где

где

Xi – сумма осадков на расчетной высоте, мм;

Xst – сумма осадков на равнинной станции, мм;

γ – плювиометрический градиент;

∆H – разность между расчетной высотой и высотой станции, м. Разность между высотами определяется по формуле

AH = Hi - Hst,

Hi – расчетная высота, м;

Hst – высота станции, м.

Ю.М. Денисов [2] для расчета талого стока горных рек использовал криволинейный вид зависимости (1)

Xi = Xst-(1 + k 1 - AH + k2 • (AH)2),

где k 1 , k 2 – эмпирические коэффициенты.

С помощью данных зависимостей можно рассчитать сумму осадков на любой высоте за любой интервал времени. Сложность возникает при задании эмпирических коэффициентов. Обычно они подбираются по виду высотных зависимостей осадков с применением регрессии или оптимизации. Рассмотрим некоторые недостатки данных схем.

Во-первых, часты случаи, когда на равнине осадки не наблюдаются, а в горах идут дожди. Рассмотренные выше схемы расчета учесть их не в состоянии, особенно при работе с малыми временными интервалами (сутки и менее).

Во-вторых, в формулах (1), (3) величина увеличения осадков в горах зависит от их количества на опорной станции. Осадки в горах, рассчитанные по данным высотной станции, оказываются выше, чем рассчитанные по данным равнинных станций.

В-третьих, расчет по (1) и (3) дает завышение сумм осадков в горах при интенсивных ливнях на равнине. Действительно, на территории гор Южной Сибири интенсивные осадки (более 30 мм в сутки) обычно выпадают при прохождении атмосферных фронтов. Они распределены достаточно равномерно в районах расположения перемещающихся фронтов и слабо изменяются при изменении высоты местности.

Методика проведения исследований . В работе по расчету гидрографов половодья сибирских рек предстояло учесть недостатки рассмотренных выше схем и определиться с методом расчета количества осадков в горной части водосбора рек в период формирования весеннего половодья. В целях разработки районной схемы расчета осадков в горах Саян в весенне-летний период были использованы все имеющиеся в Среднесибирском УГМС данные наблюдений за атмосферными осадками на метеорологических станциях и гидрометеорологических постах. В бассейнах Красноярского и Саяно-Шушенского водохранилищ в разное время велись наблюдения за количеством осадков на 93 пунктах, в основном расположенных в долинах. Самой высокой является станция Оленья речка (высота 1404 м), в то время как максимальные высоты местности достигают 3500 м и выше.

В исследуемой территории весеннее половодье в горах продолжается с апреля по июль. Суммы осадков за этот период в пунктах наблюдений приводились к среднемноголетним значениям.

Согласно [3], количественно уменьшение осадков на подветренной равнине соизмеримо с увеличением осадков на возвышенностях, а увеличение осадков на наветренных склонах в значительной мере компенсируется их уменьшением на подветренной части территории. Это позволяет выделить на территории бассейна Енисейских водохранилищ однородные районы по характеру среднего многолетнего высотного распределения осадков в период снеготаяния. На рисунке 1 представлена связь рассчитанных сумм осадков от высоты. По виду связи выделены три высотные зависимости, соответствующие трем характерным районам бассейна водохранилищ Енисейских ГЭС.

Первая зависимость имеет наибольший градиент увеличения осадков с высотой, территориально соответствует правобережью Енисея, в пределах бассейнов р. Сыда, Туба, Оя. Это самый увлажненный район бассейна.

Вторая зависимость характеризуется меньшими градиентами, соответствует левобережью р. Енисей в пределах бассейнов р. Абакан, Кантегир, Ус. Данный район также достаточно увлажнен, но в этом отношении заметно уступает первому.

Третья зависимость характеризует распределение весенних осадков южнее хребта Западного Саяна, в пределах Республики Тыва. Данный район вследствие континтальности климата и наличия дождевой тени от хребтов Алтая наименее увлажнен. Здесь наблюдаются и наименьшие градиенты увеличения осадков с высотой.

3           21

(О

Е

0Q

0      100     200     300     400     500     600     700     800

Сумма осадков, мм

Рис. 1. Зависимость средних многолетних сумм осадков за период апрель-июль от высоты местности: 1 – район “Правобережье”; 2 – район “Левобережье”; 3 – район “Тыва”

Поле точек наблюденных значений аппроксимированы аналитическими зависимостями (в нашем случае были выбраны полиномы 2-й и 3-й степени). В областях, не обоснованных данными наблюдений (выше 1500 м), связь была проведена согласно ранее проведенным исследованиям и общим представлениям о распределении осадков в высокогорьях [4–6].

В [6] представлены результаты расчета зависимостей годовых осадков в исследуемом бассейне от высоты местности по методу водного баланса. На высотах свыше 1500 м наблюдается плавное снижение интенсивности увеличения осадков с высотой. Уменьшение осадков с высотой здесь инструментально не зафиксировано.

Уравнения районных аналитических кривых представлены в таблице. Связи характеризуют среднее увеличение осадков с высотой в обособленных физико-географических районах (рис. 2).

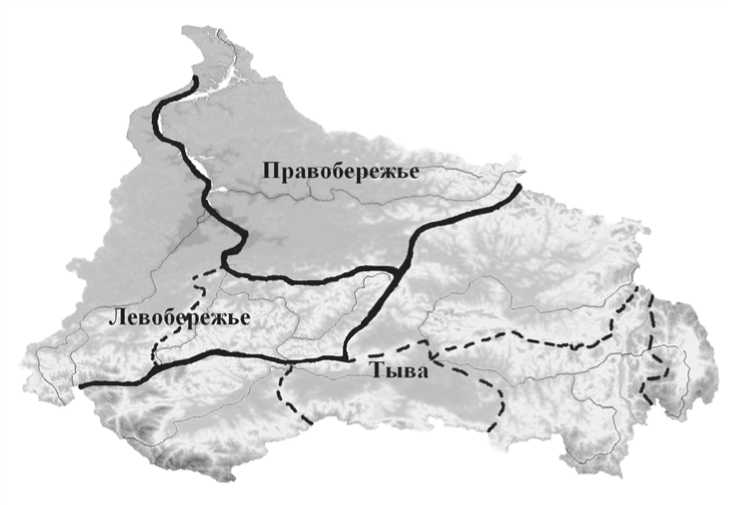
Рис. 2. Схема районирования территории по зависимости X = f(H) (пунктиром оконтурены районы из [7])

Таблица 1

Уравнения районных высотных зависимостей средних многолетних сумм осадков за период апрель-июль от высоты местности

Район	Уравнение зависимости X = f ( H )
Правобережье	X = 2.76 - 10 -8 • H 3 - 2.23 • 10 -4 • H 2 + 0.692 • H - 18
Левобережье	X = 1.63 - 10 - 8 • H 3 - 1.59 - 10 - 4 • H 2 + 0.576 • H - 24
Тыва	X = - 1.61 - 10 - 5 • H 2 + 0.125 • H + 47

В основу схемы расчета суточных сумм осадков положено предположение о том, что каждый случай выпадения осадков в однородном районе повторяет среднее многолетнее высотное распределение суммы осадков за сезон. Зная аналитическую зависимость среднего многолетнего распределения весенних осадков по высоте водосбора, суточные суммы рассчитываются по формулам:

Хг = Xst •

___ Л b - Xst Л

fb1

^ Xst)

(для Xst < 30 мм);

Xi = Xst          (для Xst > 30 мм), где Xi , Xst – средние многолетние суммы осадков на расчетной высоте и на высоте станции, мм, определяются по формулам связи X = f (H) из таблицы 1;

b – эмпирический коэффициент.

В данной схеме вместо плювиометрического градиента использовано отношение средних многолетних сумм осадков на разных высотах.

Коэффициент b характеризует пороговую суточную величину осадков на равнинной станции, при которой ослабляется градиент увеличения осадков вверх по склону. Экспериментально для района исследований принято b =30 мм. Таким образом, при выпадении на равнине осадков, близких к 30 мм и более, показатель степени обнуляется, а градиент увеличения осадков с высотой приближается к нулю (т.е. Xi = Xst ). Данная схема подтверждается данными наблюдений.

Результаты исследований. Анализ применимости уравнения (4) в практике расчетов гидрографа стока проверен по многолетним рядам (20 лет) суточных сумм осадков (с апреля по июль) для 9 пар станций (по три пары на каждый выделенный район). Для каждой пары станций средняя квадратическая ошибка расчета осадков по уравнению (4) ниже, чем по уравнениям (1) и (3), а коэффициент корреляции на десятую долю выше.

Разработанная схема имеет преимущество по сравнению с методом плювиометрических градиентов. Выпадение осадков в горах при их отсутствии на равнине компенсируется в предлагаемой схеме некоторым их завышением в дни с их наличием.