Расчет волнового сопротивления прямоугольного волновода с двухслойным заполнением

1. Вывод выражения для волнового сопротивления

На рис. 1 изображено поперечное сечение прямоугольного волновода с двухслойным заполнением (ПВДЗ). В данной направляющей струк- туре могут распространяться продольные электрические (LE) и продольные магнитные (LM) волны [1]. У LE-волн отсутствует перпендику- лярная к границе раздела слоев составляющая напряженности электрического поля (Ex ^ 0).

В случае LM- волн выполняется условие H x = 0.

В распределении поля любой LE _{0 m} -волны, ( m = 1,2, ...) имеется три компоненты напряженностей. Их комплексные амплитуды в области j

(рис. 1) выражаются следующим образом:

н Хj ) = -YLa ⁽ j ) s ⁽ j ) ( x ) e ^- i ^Y z , а⁽⁾

H z j ) = a ⁽ j ) c ⁽ j ) ( x ) e ^- i ^Y z ,

( j )

E yj )=- W°^ a ^{( j} ) _s ^{( j} ) ( x ) e - i ^у z ,    ( j = 1,2 ) .

a⁽ j )

Здесь A ⁽¹⁾

A ⁽²⁾ —

произвольные постоянные; i – k = ©^Sq^ — волновое число свободного пространства; to — круговая частота колебаний; Sq и Цо — электрическая и магнитная постоянные; у - постоянная распространения волны;

6 «==< ^j )- i j ,   ( j = 1,2 )

– комплексная относительная диэлектрическая проницаемость материала заполнения области j (рис. 1); s(j), Ц(j), G(j) — его относительные диэлектрическая и магнитная проницаемости, а также удельная проводимость;

c ⁽¹⁾ ( x ) = cos ( a⁽¹⁾ x ) ,

c ⁽²⁾ ( x ) = cos ^a⁽²⁾ ( x - a 2 ) ],

s ⁽¹⁾ ( x ) = sin ( a⁽¹⁾ x ) ,

s ⁽²⁾ ( x ) = sin ^a⁽²⁾ ( x - a 2 ) ].

Требование непрерывности тангенциальных составляющих напряженностей электрического и магнитного полей волны на границе раздела слоев мнимая единица;

a^{( j} ) = k ² s ^{( j} )ц^{( j} ) - у²,     ( j = 1,2 ) ;                   (4)

( е У ¹)- е У ²))      = о,

'               ' x = a1

( h Z ¹)- h Z ²))     = 0

'               ' x = a 1

Рис. 1

приводит к однородной системе линейных алге-

браических уравнений относительно

( 1 )      ( 2 )

ных множителей A , A

амплитуд-

k ^ _S(1) (а. 1 д(1) - k ^^²) _S(2) (a. 1 д(2) - 0

( 1 ) ^{s   ( a} 1 ) ^A         ( 2 ) ^{s ( a} 1 ) ^{A      0} ,

a( )                     a( )

c ⁽¹⁾ ( a 1 ) A ⁽¹⁾- c ⁽²⁾ ( a 1 ) A ⁽²⁾ = 0.

Условие совместности системы (5) дает диспер-

сионное уравнение для определения постоянных распространения волн LE°m, (m = 1,2,...)

^ « ⁽¹⁾ ( « 1 ) c ^{( 2,}( a , ) -

” ₍ 3 )                                                   (6)

к 1 ¹ ( 1 )        ( 2 )

(2У c ( « 1 ) ^{5 (} ) ( « 1 ) = °.

а( 7

	' b
	J E y4 x ° , y , z ) dy ,
U =	°
	b
	J E y 2^ ( x ° , y , z ) dy,
	. °

( ^x ° <  « 1 ) ,

( ^x ° >  « 1 ) .

С учетом выражения (3), имеем

Магнитное поле волны LE ° _m , ( m = 1, 2, ...) не содержит поперечной компоненты напряженности магнитного поля H_y , параллельной вертикальным стенкам волновода. Как следствие, на этих стенках не протекает продольный ток. Плотность

— < юц °₁1<¹> Ь a ( 1 ) _s ( i )₍ x ° ) e - i _T z , a⁽¹⁾

-    . '^ A ⁽ 2 ) 5 ⁽ 2 ) ( x ° ) e - i , z ,

a(2)

( ^x ° <  « 1 ) ,

( ^x ° >  « 1 ) .

продольного тока на горизонтальных стенках

Принимая во внимание соотношения (1), (7), (10), получаем

волновода

J zj ) ( x , °, z ) = - H xj ) ( x , °, z ) , j Zj ) ( x , b , z ) = h X j ) ( x , b , z ) ,     ( j = 1,2 ) .

I = - i у

A (1) ^{1 -} c ^{(1) (} « 1 ) - A (2) ^{1 -} c ^{(2) (} « 1 ) ( a⁽¹⁾ ) 2                ( a⁽²⁾ ) 2

e ^- i ^{Y z} . (12)

Тем самым, процесс распространения волны LE ° _m , ( m = 1,2, ...) ПВДЗ допускает интерпретацию в рамках модели длинной линии. Ее прово-

Выразим амплитудный

первого уравнения (5).

множитель

A ⁽²⁾ из

дники следует отождествлять с горизонтальными стенками волновода.

Одним из основных параметров длинной линии является ее волновое сопротивление

Z в = UI .                                     (8)

Здесь U и I – комплексные амплитуды волн напряжения и тока, протекающих в длинной линии. В случае LE ° _m -волн ПВДЗ, ( m = 1,2,... ) величины U и I определяются следующим образом

U = J Edl,(9)

L a1a2

I = J Jz1) (x, °, z) dx + J Jz22 (x, °, z) dx.(1°)

Контур L в интеграле (9) соединяет нижнюю и верхнюю стенки волновода. Он ориентирован

( 2) _ ц⁽¹⁾а^{(2) 5 (1) (} « 1 ) ( 1 ) = _a( 1M ²) 5 ( 2 ) ( « 1 )

Подстановка (13) в равенства (11), (12) дает

- ^ _^^ ^{о ц} (¹> ь A (1 ) 5 _W( x ° ) e _, Y z , a⁽¹⁾

(x° < «1), i®ц0Ц b (1)

- a( 1 ) A

8 (1^ 0 1) ( 2 ) 5 ⁽²⁾ ( « 1 )

( x ° ) e - i ^Y z ,

( ^x ° >  « 1 ) ,

I = - ^ a№, I¹)( « 1 ) a⁽ )

⁺ n^{( 2)} _a ⁽²⁾

tg

u ( 1 )_a(¹) 11 M

tg

a ⁷ « ₁

+

a⁽²⁾ ( « 2 - « 1 )

e ^- i ^{Y z} .

перпендикулярно направлению распространения волны и расположен в плоскости x = x°, соответствующей максимальному значению амплитуды напряженности электрического поля волны. В соответствии с граничными условиями на вертикальных стенках волновода еЙ = еУ2)| = °, x=° x=« 2

такой максимум в распределении E y ( x )| всегда существует. Единственность этого экстремума уместно рассматривать в качестве условия, при котором возможно введение волнового сопротивления волны LE ° _m , ( m = 1,2,... ) ПВДЗ.

Используя определение (8), находим волновое сопротивление ПВДЗ при распространении в нем LE ° _m -волн, ( m = 1,2, ^ )

Z в

где

z =

5 521 x 0) ^{5 ( 1 )} ( « 1 ) ^{5 ( 2 )} ( x ° ) 5 ^{( 2 )} ( « 1 )

z, z,

( ^x ° <  « 1 ) ,

( ^x ° >  « 1 ) ,

kb E° Г ¹ Y ^° 1ц( 1 )_а(¹)

tg

a ⁷ « 1

+

⁺ ( 2 ) ( 2 ) tg ц⁽ )a⁽ )

Y (2)/        \Ъ-1

a ’ ( a 2 - a 1 )

.

Точке максимума x ₀ амплитуды напряженности электрического поля волны E ( x , y, 0 ) соответствует ноль производной одной из функ-

ций | s ⁽¹⁾ ( x )| или | s ⁽²⁾ ( x )|. Для

этих производных

Y m = ^ k²s ⁽²⁾Ц⁽²⁾ - ( л m/a 2 ) ²,    ( m = 1,2... ) .

Здесь величина Y 1 совпадает с постоянной распространения (16) волны H ₁₀, распространяющейся в прямоугольном волноводе, заполненном

( 2 )     ( 2 )

материалом с проницаемостями s , ц . Полагая в (14) a ₁ = 0, имеем

можно получить следующие выражения:

dbs ⁽¹⁾⁽ x )l= x

2	s (1) ( x )

х

Z = kb ц⁽²⁾_a⁽²⁾ J^ 0 sinP 2 ⁾^ a 2£ x 0}] 2 ^Y      V^e 0     sin² ( a⁽²⁾ a 2/2 )

.

х ^ Re ( а⁽¹⁾ ) + Im ( а⁽¹⁾ );

J sin 2 Re ( a⁽¹⁾ ) x "  sh 2 Im ( a⁽¹⁾ ) x } ,

+

dh ⁽²⁾ ( x ) = x

х

2	s (2) ( x )

Чтобы привести равенство (17) к виду (15), необходимо выполнить замену Y = Y 1 , а⁽²⁾ = л/ a 2 и учесть, что в данном случае функция s ⁽²⁾ ( x ) в формуле (3) достигает максимального значения в точке x 0 = a 2/ 2.

Аналогичным образом можно показать, что предельный переход a 1 ^ a 2 переводит (14) в

выражение (15), в котором необходимо

х ^ Re ( а⁽²⁾ ) + Im ( а⁽²⁾ ):

sin 2 Re

x a ² ) +

sh 2 Im ( a⁽²⁾ ) ( x - a 2 ) } .

Волновое сопротивление прямоугольного волновода с однородным заполнением при протекании в нем волны H ₁₀ [2]

Z в

_ n b ц 0 к ц

² a V ^s 0 ^Y h 10

.

Здесь a и b – поперечные размеры экрана волновода ( a >  b ) ;

^Y H 10 =

— постоянная распространения волны Н ю; s -комплексная относительная диэлектрическая проницаемость материала заполнения; ц — его относительная магнитная проницаемость.

Легко убедиться в том, что при смещении границы раздела слоев x = a i (рис. 1) к одной из вертикальных стенок экрана формула (14) для волнового сопротивления ПВДЗ переходит в равенство (15).

Если a i ^ 0, то обращается в ноль первое слагаемое в левой части (6). В результате дисперсионное уравнение (6) принимает вид

sin ( a⁽²⁾ a 2 )

а(2)

или

= 0,

а⁽²⁾ a 2 =п m ,    ( m = 1,2,... ) .

С учетом (4) получаем следующие значения постоянных распространения LE- волн ПВДЗ

нить следующие подстановки: ц = ц(1)

При ПВДЗ галось,

.

a = a 2 ,

выпол-

( 1 ) s = s ,

2. Результаты расчетов

выполнении расчетов размеры

составляли: b = 1 см, a 2 = 2 b .

что

заполнение

заполнения

экрана

область 2 (рис. 1) имеет

Предпола-воздушное

( s⁽²⁾ = ц⁽²⁾ = 1, g^{( 2 )} = 0 ) . Материал

области 1

–

слабо легированный

примесью карбид кремния ( SiC ) n -типа (политип 3 C ). При температуре T = 300 К числовые значения параметров этого полупроводника составляют [3]: s⁽¹⁾ = 2,6, ц⁽¹⁾ = 1, собственная концен- 5   –3

трация электронов проводимости n i = 10 м , подвижности электронов проводимости и дырок ц _e = 0,1 м² / (В ■ с), ц _h = 0, 006 м² / (В ■ с). Карбид кремния моделировался как линейный диэлектрик с потерями. Его удельная проводимость вычислялась по формуле [4]

G⁽¹⁾ = e ( П е Ц e + n h Ц h ) .

Здесь e – абсолютное значение заряда электрона; n_e и n_h – концентрации электронов проводимости и дырок, определяемые равенствами

n e = ¹ ( N d +4-

' N + 4 n 2 ) ,

n h n i !^пе ;

N_d – концентрация донорной примеси, в качестве которой может использоваться элемент пятой группы периодической системы ( N , P , As , Sb , Bi ) или железо [5].

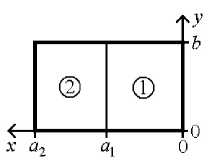
На рис. 2 и 3 изображены дисперсионные характеристики трех низших LE _{0 m} - волн ПВДЗ, – зависимости действительных и мнимых частей

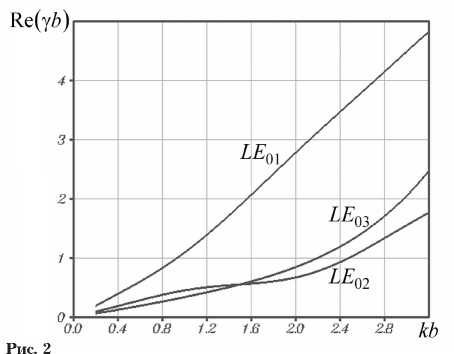
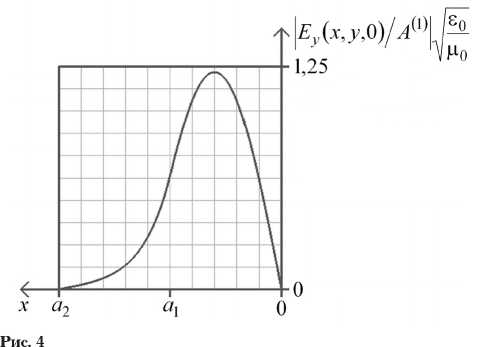
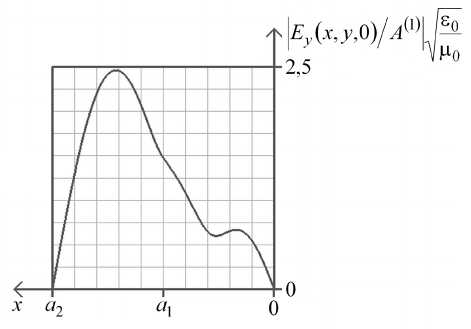
Рис. 5

нормированных постоянных распространения волн у от нормированного волнового числа свободного пространства k. При этом координата границы раздела областей 1 и 2 ay = b, концентрация донорной примеси в полупроводнике Nd = 1020 м 3. Нумерация волн осуществляется в порядке убывания мнимых частей их постоянных распространения на низких частотах. Точнее, если при ay = b справедливо соотношение lim Im (у m) > lim Im (у n), (m, n = 1,2, .„), k >0          k >0

то при любых значениях параметров a 1 (0 <  a 1 < <  a 2 ) и k индексы m и n в обозначениях волн LE o _m , LE 0 n удовлетворяют условию m <  n .

Введем критическое значение волнового числа k , предполагая, что при k = k _к р действительная и мнимая части постоянной распространения волны у равны по модулю. Например, нормированные параметры k _кр волн LE ₀₁ – LE ₀₃ составляют: k b = 1,4, k b = 2,7, k b = 3,3. Тем са- кр,1           кр,2           кр,3

мым, можно также считать, что низшие LE _{0 m} -волны ПВДЗ пронумерованы в порядке возрастания их критических частот ю кр = k кр/^ £ 0 ^ 0 при условии a 1 = b .

На низких частотах координатные зависимости амплитуд компонент Ey напряженностей электрических полей волн LE0m, (m = 1,3) воспроизводят соответствующие распределения для волн Hm0, (m = 1,3) прямоугольного волновода с однородным заполнением и размерами экрана a2 х b. Соответствующие предельные значения постоянных распространения волн LE0m , (m = 1, 2, ...) легко определить из дисперсионного уравнения (6). Устремим в (6) волновое число k к нулю, предварительно поделив обе части равенства (6) на k. С учетом соотношений lim a(j) = iу, (j = 1,2),        ц(1) = ц(2), k >01

имеем sin (iYa 2) = 0, или

Y = - i n m^ 2 ,   ( m = 1,2, — ) .

Выражения (18) соответствуют низкочастотным значениям постоянных распространения волн Hm0 прямоугольного волновода с однородным заполнением. Следует отметить, что предельные значения (18) величины у не зависят от параметров £(j), ц(j), g(j), (j = 1,2) материалов заполнения ПВДЗ.

На рис. 4–6 приведены распределения нормированных амплитуд напряженностей элек-

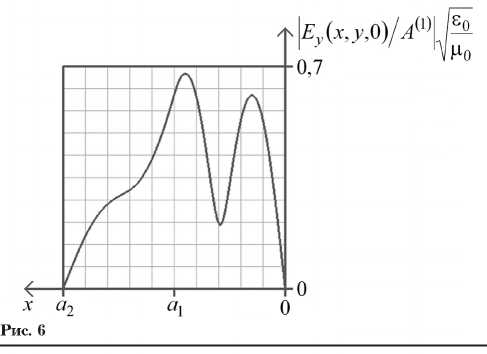
трических полей волн LE oi - LE 03 при a 1 = b , N d = 10 20 м^-3, kb = 3,2. Как известно, граница раздела сред обладает отражающими свойствами, удерживая энергию волны в среде с большей оптической плотностью. Именно такое влияние оказывает плоскость x = a 1 , разделяющая слои, на волны LE ₀₁ и LE ₀₃ (рис. 4, 6). Поле волны LE ₀₂ (рис. 5), напротив, сосредоточено в области 2, имеющей воздушное заполнение. Эта волна воспринимает границу раздела сред как экранирующую поверхность проводящего слоя 1.

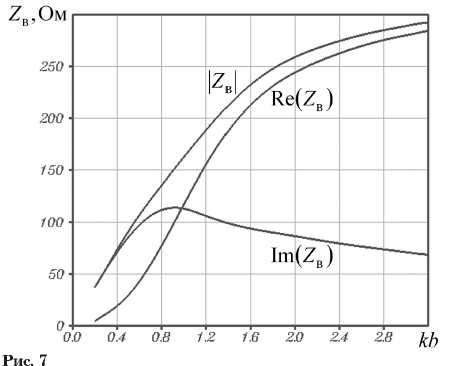
На рис. 7 представлены зависимости действительной и мнимой частей волнового сопротивления, а также модуля Z _в волны LE ₀₁ от нормированного волнового числа свободного пространства к при a 1 = b , N d = 10²⁰ м ³. Что касается волн LE ₀₂ и LE ₀₃, то при выбранных значениях параметров волновода в распределениях | E_y ( x )| амплитуд компонент напряженностей их электрических полей имеется по два максимума (рис. 5, 6). Тем самым, для этих волн не представляется возможным определить волновое сопротивление на основе изложенной методики.

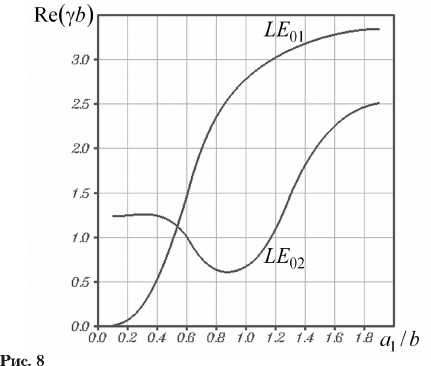
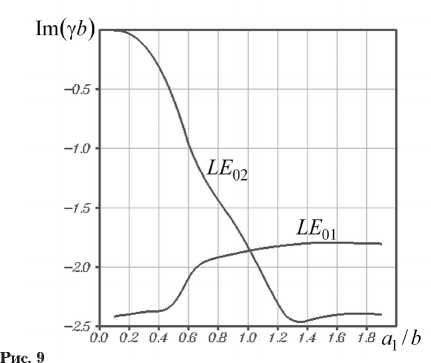
На рис. 8 и 9 изображены зависимости действительных и мнимых частей постоянных рас- пространения волн LE01 и LE02 от толщины слоя 1 (рис. 1) при kb = 2, Nd = 1020 м 3. В случае a1 / b = a2 / b = 2 ПВДЗ превращается в прямоугольный волновод, однородно заполненный полупроводником. При a1 ^ a2 волны LE01 и LE02 ПВДЗ переходят, соответственно, в волны H10 и H20 такой однородно заполненной линии передачи.

С уменьшением параметра a ₁ от значения a ₂ обе волны по прежнему стремятся концентрировать свои поля в области 1, запол н енно й о птически более плотным материалом. Однако, по мере сужения слоя полупроводника это становится все более проблематичным. Как следствие, уменьшаются действительные части постоянных распространения волн. При этом коэффициент затухания |lm ( у)| каждой из волн возрастает незначительно, что обусловлено уменьшением доли поглощающего материала в заполнении волновода.

Волне LE ₀₂, с ее двумя максимумами в поперечном распределении амплитуды напряженности электрического поля, труднее удержаться в сужающемся слое полупроводника. Эта вол-

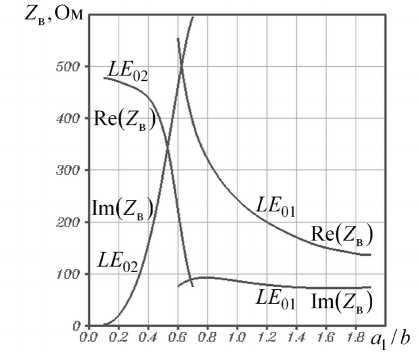
Рис. 10

на первой вытесняется в область 2, имеющую воздушное заполнение. При ai ^ 0 волна LE02 трансформируется в основную волну (H10) прямоугольного волновода, однородно заполненного воздухом. На нормированной частоте kb = 2 волна H10 является распространяющейся. Ее нормированная постоянная распространения уb = ^(kb)2 б(2)ц(2) - (лba2 )2 « 1,2380. (19) Следует заметить, что с уменьшением параметра a на интервале (0, a2 ) волна LE02 преобразуется из H20-волны в волну H10 типа. При этом количество максимумов в поперечном распределении амплитуды напряженности ее электрического поля сокращается с двух до одного. Подобная трансформация поля волны сказывается и на ее спектральных параметрах. Уменьшение действительной и мнимой частей постоянной распространения волны сменяется их ростом. В частности, Im (у) ^ 0 при a1 ^ 0.

Поле волны LE01 вытесняется из области 1 в область 2 при существенно меньшей толщине a1 слоя полупроводника. Однако трансформироваться в основную волну H10 прямоугольно- го волновода с воздушным заполнением уже не представляется возможным. Ведь такое преобразование претерпела волна LE02. Поэтому при а1 ^ 0 волна LE01 превращается в квази-H20-волну такого волновода, увеличивая с одного до двух количество максимумов в поперечном распределении амплитуды своего электрического поля. На расчетной частоте волна H20 прямоугольного волновода с воздушным заполнением является затухающей. Ее нормированная постоянная распространения уb = (kb)2 б(2)ц(2) -(2пba2 )2 « -i ■ 2,4227. (20)

Рис. 8, 9 позволяют убедиться в том, что при a 1 ^ 0 постоянные распространения волн LE 01 и LE ₀₂ стремятся к предельным значениям (19), (20).

На рис. 10 приведены зависимости действительных и мнимых частей волновых сопротивлений волн LE ₀₁, LE ₀₂ от параметра a ₁ при kb = 2, 20  –3

Nd = 10 м . Внутри диапазона значений аргумента (0,1 < a1 /b < 1,9) обрыв любой из представленных здесь кривых означает появление второго максимума в поперечном распределе- нии амплитуды напряженности электрического поля соответствующей волны.

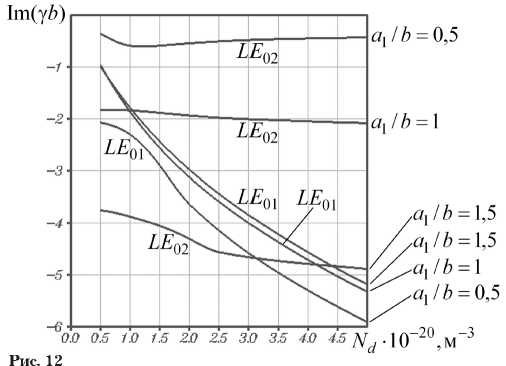
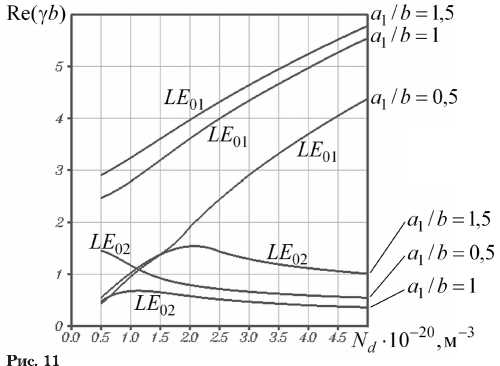
Зависимости действительных и мнимых ча- стей постоянных распространения волн LE01 и LE02 от концентрации донорной примеси в полупроводнике Nd изображены на рис. 11, 12. При этом нормированное волновое число свободного пространства kb = 2. С увеличением параметра

N d в диапазоне ( 5 ■ 10¹⁹м 3 , 5 ■ 10²⁰м ³ ) удельная ^V                              (1)       ⁷

проводимость полупроводника ст возрастает от

0,8011 См/м до 8,011 См/м, изменяясь практи- чески по линейному закону.

Как было отмечено выше, при определенных условиях поля некоторых волн ПВДЗ концентрируются в области 2 (рис. 1), имеющей воз-

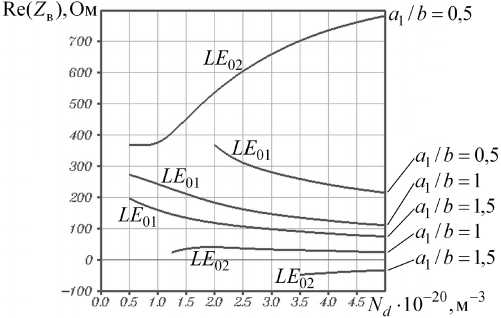
Рис. 13

душное заполнение. От волны подобного рода естественно ожидать слабой зависимости постоянной распространения у от удельной проводи- мости ст и концентрации примеси в полупрово-

днике N_d . Затухание такой волны

|Im ( у)| долж-

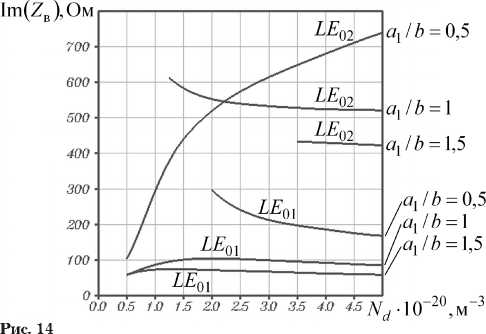
но существенно возрастать с увеличением a ₁ за счет сужения области локализации поля волны. Рис. 11, 12 позволяют утверждать, что перечисленными свойствами обладает волна LE ₀₂ ПВДЗ. Что касается волны LE ₀₁, то ее свойства прямо противоположны. Тем самым, поле волны LE ₀₁ сосредоточено в слое полупроводника.

На рис. 13, 14 приведены зависимости действительных и мнимых частей волновых сопротивлений волн LE 01 , LE 02 от N d при kb = 2. Об-

рыв линии внутри диапазона

трации примеси ( 5 ■ 10¹⁹м

.-3

означает появление второго

значений концен-< N d < 5 ■ 10²⁰м ^{- 3} ) максимума в по-

перечном распределении амплитуды напряженности электрического поля соответствующей

волны.

Как следует из рис. 13, при a ^ b = 1,5 действительная часть волнового сопротивления волны LE ₀₂ оказалась отрицательной. Возможно ли такое? Для ответа на этот вопрос обратимся к соотношению [6]

_ R _п + i to L _п , в    G g п + i to C п

связывающему волновое сопротивление с параметрами длинной линии. Здесь L _п и C _п – погонные индуктивность и емкость линии передачи. Погонные сопротивление R _п и проводимость G _п, соответственно, учитывают потери в проводниках направляющей структуры и в разделяющем их изоляторе.

Соотношение (21) можно привести к виду

2    R п G п + to² L п C п + ito ( L п G п - C п R „ )

Z в               ^2 г^Г²             .

^G п + ^to C п

Отсюда с очевидностью следует, что действительная часть величины Z2 положительна. То в же самое можно сказать и о самом волновом сопротивлении. Тем самым, при значениях параметров a1 bb = 1, 5, kb = 2, Nd > 3 ■ 1020 м 3 изложенную модель длинной линии нельзя признать адекватно описывающей распространение волны LE02 ПВДЗ. Таким образом, единственность максимума в поперечном распределении амплитуды напряженности электрического поля волны LE0m ПВДЗ является необходимым (но не достаточным) условием применимости к этой волне данной модели.