Расчет взаимодействия элементов метаструктуры на основе метода Гаусса – Зейделя

Под метаматериалами понимают материалы, создающиеся на основе внедрения в диэлектрик различных включений определенной конфигурации. Эти включения можно рассматривать как атомы либо молекулы чрезвычайно больших размеров. Частным случаем метаматериала являются киральные и бианизотропные структуры [1]. Теория киральных структур в настоящее время достаточно активно развивается. Как правило, исследование киральных сред осуществляется с помощью феноменологической теории, материальные уравнения которой имеют вид [2]

D = б E + i X H, В = Ц H ± i х E .

В данных выражениях верхние знаки соответствуют киральной среде на основе спиралей с правой закруткой, а нижние знаки – среде на основе левовинтовых спиралей. Константа χ называется параметром киральности. Достоинством исследования киральных структур с помощью феноменологических уравнений является относительная простота аналитических выводов. Но здесь следует отметить усредненный характер уравнений, необходимость знания параметра киральности и его частотной зависимости для конкретной среды, малость размеров киральных элементов в сравнении с длиной волны и боль- шое расстояние между элементами, позволяющее пренебречь их взаимодействием.

Корректное описание близко расположенных элементов, соизмеримых с длиной волны, возможно только на основе строгого электродинамического подхода, который избавляет от необходимости введения параметра киральности, снимает ограничения на размер элементов и расстояния между ними, а также дает корректное описание ближней зоны киральных элементов.

Остановимся на взаимодействии элементов. Сложность расчета в отсутствие взаимодействия составляет O ( N ), где N – число элементов структуры. Сложность расчета в присутствии взаимодействия равна O ( N ²), т. е. возрастает квадратично в зависимости от числа элементов. Таким образом, расчет структур со значительным числом элементов представляет собой проблему даже для современных ЭВМ и требует огромных затрат оперативной памяти.

Вместе с тем взаимодействие присутствует всегда, и при решении вопроса о пренебрежении им прежде всего важна количественная оценка. По этой причине актуальной задачей является построение метода расчета взаимодействия с возможностью его количественной оценки.

В данной статье в качестве основы для расчета взаимодействия предлагается использование

модификации метода Гаусса – Зейделя [3], оперирующего с матрицами собственных и взаимных импедансов, образующих общую матрицу системы линейных алгебраических уравнений (СЛАУ). Метод применяется для решения задачи дифракции на тонком слое метаматериала, состоящего из двойных разомкнутых колец. Ранее в [4] была рассчитана система, состоящая из двух взаимодействующих колец, а в [5] – произведено обобщение на случай произвольного числа колец (геометрически киральная структура). Математическая модель метаматериала, рассматривающаяся в данной статье, построена на основе интегральных преставлений электромагнитного поля (ИП ЭМП [5]). Исследована зависимость скорости сходимости итерационного процесса при различных соотношениях размера элементов к расстоянию между ними.

1. Модифицированный метод Гаусса – Зейделя

Решение электродинамических задач методом интегральных уравнений (ИУ) осуществляется, как правило, сведением ИУ к СЛАУ. СЛАУ можно записать в матричной форме:

——

A X = B ,                                    (1)

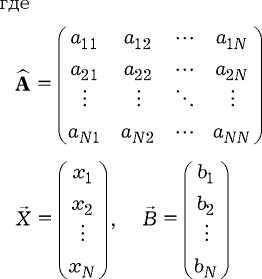
– соответственно матрица СЛАУ, вектор неизвестных элементов и вектор воздействия (правая часть СЛАУ).

Метод Гаусса – Зейделя применяется для итерационного решения СЛАУ. Представим матрицу A в виде суммы матриц L * и U : ^  ^   ^

A = L, + U ,

*, где

[ "11   0   ™   0

L* = "21  "22  Г   0,

.              .              ..

V " N 1   " N 2   ^Г

Г 0

a 12 0

" , N 1

" 2 N

V00 и перепишем СЛАУ (1) следующим образом:

-^. —.       —.     -^~ —.

L * X = B - U X .

Умножая обе части полученного равенства на матрицу, обратную матрице Ij* , и обозначая через XX ⁽ k ) старое приближение к решению, а че- ( к + 1)

рез X – новое, имеем:

X ⁽ k ^{+ 1)} = ЬЛ B - U X ⁽ k ) ).

Матрица Ij* легко обращается, поэтому данное выражение можно записать поэлементно:

(к+1) = 1 xi aii

b i V

- y a ij x jk ) - £ " ij x jk ^{+ 1)}

j >  i           j <  i            ,

i = 1,2, _ , N .

В отличие от метода простой итерации [3], метод Гаусса – Зейделя использует не только старое приближение X(k), но и ранее вычисленные элементы x(к+1) для получения нового приближения X(k+1), что приводит к увеличению ско- рости сходимости итерационного процесса.

Метод гарантирует сходимость при условии диагонального преобладания матрицы СЛАУ:

I " ii l > Е l " ij| j * i

Обобщим теперь метод Гаусса – Зейделя на случай электродинамических задач. Обычно система интегральных уравнений сводится к

СЛАУ вида:

~^^—*       —*

Z Z = E ,

где

Z =

"

^z 11

^z 21

vs z12

z 22

z1 N z2 N jS                  jS                                 J'S

V ^z N 1 ^z N 2 ^{Г z} NN J

— i1

i ² V — N J

—

E =

— 1 e 2

—

V e N J

– соответственно обобщенные матрицы импе-дансов, токов и напряжений; N – количество излучателей в системе;

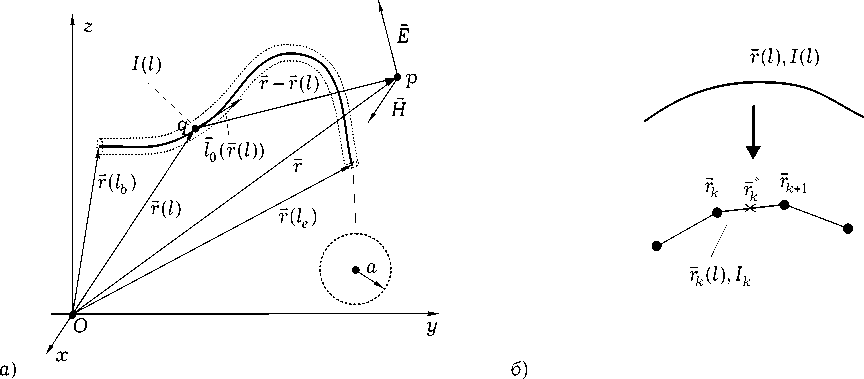
Рис. 1. Тонкопроволочная структура ( а ) и линеаризация ее образующей ( б )

' Z¹¹   Z ¹²    ^   ^{Z 1} Nj"

Z 21    ^Z 22   •"   ^Z 2 Nj

vs

"                        "                     "                  "

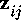
Z N -1 Z N 2 "' ZNN,.

V i i               i j 7

' I 1 )

—*

i j =

I ₂

IN;

V j 7

— ej =

[ E 1

E 2

E N

V j 7

– соответственно матрица взаимных импедансов i-го и j-го излучателей, матрицы проекционных функций собственных токов и собственных напряжений j-го излучателя; Ni – число проекционных функций на i-м излучателе; Nj – число проекционных функций на j-м излучателе.

В этом случае итерационную процедуру можно построить по формуле, аналогичной (2):

^— ( k + 1) _ ; ^— Vw ^— ( k ) Vw ^— ( k + 1)

ii    = yiei -Lwiji -Lwijij    , j>i            j

i = 1,_, N, где

- 1

y =z , w =yz i ij , ij i ij

– соответственно матрицы собственных адми- тансов и весовые матрицы.

Данная процедура в общем случае имеет следующие свойства:

• •    Позволяет произвести оценку степени взаимодействия элементов по скорости сходимости итерационного процесса;

• •    Позволяет оперировать матрицами взаимных и собственных импедансов, а не общей матрицей системы;

• •    Обращения требуют только матрицы собственных импедансов, имеющие, как правило, небольшой размер.

В частных случаях у метода появляются дополнительные достоинства:

• •    Необходимость обращения только одной матрицы собственных импедансов в случае, когда среда образована одинаковыми элементами;

• •    Снижение числа существенных весовых матриц в случае бианизотропной среды. Под существенными понимаются матрицы, необходимые для построения общей матрицы СЛАУ.

• 2. Интегральные представления электромагнитного поля

Все это позволяет существенно сократить затраты машинных ресурсов и времени.

Построение математической модели и определение матриц собственных и взаимных импедан-сов удобно осуществлять в рамках интегрального представления электромагнитного поля (ИП ЭМП).

В [5] из общего интегро-дифференциального представления получены ИП ЭМП тонкопроволочной структуры. ТПС представляет собой идеально проводящую бесконечно тонкую металлическую трубку радиуса a и длиной L , произвольно расположенную в пространстве и не имеющую самопересечений (рис. 1, а ). Считается, что объемная плотность тока — , определенная лишь на образующей ТПС и возникающая под действием стороннего электрического поля E — ⁽ in ) , имеет только продольную составляющую, поэтому ее можно записать в виде ^—

• —— (qq )= l⁰^ I ( l )5( — ' - r ( l )).

2n a

Здесь l o (7 ( l )) — единичный вектор касательной на образующей L , описывающейся радиус-вектором ⁷ ( l ), определяется как

• ⁷ z-        dr ( l )

l ₀( r ( l )) =         ;

dl l е [lb, le ] - натуральный параметр на образующей (в дальнейшем l будем также называть продольной координатой, lb – координатой начала ТПС, le – координатой ее конца); I(l) – распределение тока по образующей; 5(x) — дельтафункция. Также предполагается, что при любых значениях l радиус a много меньше радиуса кривизны р(l) =| d-)(l) / dl | .

Граничное условие для ТПС ставится следующим образом:

Ы - ( l )) ( E ⁽ in ) ( 7(l )) + E( - ( l )) ) = 0.                     (5)

ИП ЭМП от тока I ( l ), протекающего по образующей L ТПС, имеет вид

F( 7 )= I ( l ') K F ( 7 , r ( l )) dl ‘, F = E , H ,             (6)

L здесь

KE (7, 7(l)) =     1 -)(lk2Ga (7, 7(l')) + ik ^

+ A(( 7 - 7 ( l ')) B a ( 7 , 7 ( l ')))];

d l                          )

K H ( 7 , 7 ( l )) = ( ( 7 - 7 ( l '))X l o (l ') ) B a ( 7 , 7 ( l '))

– ядра интегрального представления; W_c – волновое сопротивление среды; k – ее волновое число;

B = - SkR±1 G , G ( R ) = exp ⁽~^ikR > , _R ² 4n R

G ( R ) имеет смысл функции Грина свободного пространства; R ( 7 , ⁷ ') = |7 - ⁷ '| — расстояние между точкой источника и точкой наблюдения;

F a ( 7 , 7 ( l ')) = F ( R a ( 7 , 7 ( l '))),    F = G , B

– компоненты ядер;

R_a ( 7 , 7 ( l ')) = 7l 7 - 7 ( l ') |² + a a

– регуляризированное расстояние между точкой источника и точкой наблюдения; в качестве параметра регуляризации выступает радиус a провода.

В случае подстановки граничного условия (5) в (6) при F = E получается известное интегральное уравнение для определения тока произвольной тонкопроволочной структуры, приведенное, например, в [6].

Для упрощения дальнейших выводов будем записывать ИП (6) в компактной форме:

F ( 7 ) = F a ( 7 ; 7 ( l ), I ), F = E , H ,                      (7)

где явно указываются параметры представления – распределение тока I , образующая ТП-структуры 7 ( l ) и радиус провода a . В дальнейшем индекс a при отсутствии в нем необходимости будем опускать.

При численном моделировании гораздо удобнее работать с дискретными моделями, поэтому осуществим дискретизацию интегральных представлений (6).

Пусть r ( l ) — радиус-вектор образующей ТПС, l е [ l b , l e ]; L = l e - l b — длина образующей. Разобъ-ем образующую на сегменты длиной А (рис. 1, б ). Если число сегментов равно N , то А = L / ( N + 1). Введем индексы:

k = 1, ^ , N ; k' = 1, ^ , N +1.

В данных обозначениях l^' = А( к' -1) — значения натурального параметра на границе к -1 и к -го сегментов, 7 к> = ⁷ ( l k - ) — соответствующий радиус-вектор, l * = l k + А /2 — значение натурального параметра в центре k -го сегмента, 7 _*    7 _*

r_k = r ( l_k ) – соответствующий радиус-вектор. Осуществляя линеаризацию образующей, уравнение сегмента можно записать следующим образом:

7 k ( l ) = 7 * + l ok l ; l е [-А /2, А /2],               (8)

здесь:

7 *      + 1 ^{+ 7} . ⁷ _⁷ + 1 ^{- 7}

⁷k          2      ; ' o k         А .

Далее, полагая, что А ^ X, будем считать распределение тока на каждом сегменте равномерным:

I ( l ) = I k ; l е [ l k -А/2, l k +А/2].

Подставляя данное выражение и выражение (8) в интегральное представление (6), получаем дискретизированное интегральное представление ЭМП:

F ( 7 )= '^ II k K А , ^F ( 7 , 7 k ),    F = E , H ;             (9)

k =1

здесь:

А /2

K ^А , ^F ( 7 , 7 k )= J K F ( 7 , 7 k ( l )) dl , F = E , H

-А /2

– весовые коэффициенты.

В дальнейшем дискретизированные ИП по аналогии с (7) будем записывать в компактном виде:

F(r) = F a ( r; r k , I k );    F - E , H ,                   (10)

где явно указываются параметры представления — координаты границ сегментов k , значения тока I k на сегментах, а также длина сегмента А и радиус провода a .

Выражение (7) описывает ЭМП одиночной ТПС. Как правило, мы имеем дело с некоторой совокупностью J тонкопроволочных элементов:

та, r jk. — радиус-вектор, проведенный в точку сопряжения k j и k j + 1 -го сегмента j -го элемента. Тогда по аналогии с (11) на основе дискретизированных ИП (10) можно записать:

N N j _А

^F ( r) = ЕЕ ^Faj ( r ; r j , kj , I j , kj ), F-E , H .    (13)

j = 1 k j = 1 j

L ^: L 1 , L 2 , . L N ,

где L_j – образующая j -го элемента, описывающаяся радиус вектором:

Выражение (13) описывает ЭМП, создаваемое совокупностью N излучающих элементов с сегментированными образующими.

Для использования (13) необходимо знать не-

rj (l ) = XgXj (l) + У0 Yj (l) + Zg Zj (l), l e [lb.;le. ], j = 1,.N, j ej здесь Xj (l), Yj (l), Zj (l) – некоторые гладкие функции, зависящие от натурального параметра l; j – порядковый номер тонкопроволочного элемента.

Полное ЭМП такой структуры находится с помощью интегрального представления (7) с учетом принципа суперпозиции:

F(r) = E F(r; r j , I j ); F - E , H .                 (11)

j

Таким образом, (11) представляет собой ИП ЭМП сложной тонкопроволочной структуры.

В ИП (11) входят неизвестные пока токи I_j . Для их определения используем граничное условие (5) на каждом проводнике структуры. В результате получим систему интегральных уравнений следующего вида:

- l g ( r i ) E ⁽ in ) ( r i ) = Iq ( r i ) E E ( r i ; r j , I j );

j                            (12)

i , j = 1,^, N .

известные амплитуды токов I_{j , k} . В рамках метода сшивания в дискретных точках потребуем

выполнения граничного условия типа (5) в центрах сегментов. Пусть rk. — радиус-вектор, про-,i веденный в центр ki -го сегмента i-го элемента. Тогда из (13) с учетом учетом граничного условия (5) получаем систему линейных алгебраи-

ческих уравнений для определения

5        ⁵             5

- l g ( r i , ki ) E ⁽ in ) ( r i , ki ) = l o ( r i , ki ) x

I j , k _j :

N N j  А

^Х ЕЕ E a^{3 (} r i , ki ^; r j , kj , I j , kj ^{);                     (14)}

j=1kj =1 j i j j i = 1,_, N,   ki = 1,_, Ni.

Устойчивое решение достигается при соблюдении условия А j ^ 4 a j , для всех j [9].

Таким образом, в принятых ранее обозначениях для СЛАУ (3) из (14) получаем:

W„ ^   *

z ij = "kk ° (r r i , ki^}

4 ,-      2

l ₀ ( r_{j k} ) k ² Х j

Данную систему можно классифицировать как систему ИУ Фредгольма первого рода [8]. Решение подобных ИУ является некорректной математической задачей, т. е. оно может быть неустойчивым. Существует множество методов решения, обладающих определенными регу-ляризирующими свойствами. Асимптотическая корректность и регуляризирующие свойства некоторых методов рассмотрены в [9]. Наиболее

^А j /2

x J G a ( r i * ki

^-А j /2

)

, r jk. ( I )) dl + B a ( r *k. , jk. ) ; j , _j                   a , _i j , _j

J

^-*      ^-

B a ⁽ r i , ki , r j , kj ) =

простым и естественным является метод сшива-

ния в дискретных точках [10].

Введем дополнительные обозначения. Пусть

I_{j , k} – значение амплитуды тока на k_j -м сегменте j -го элемента, k j =1,..., N j , где N j — число

сегментов j -го элемента; А j — длина сегментов

j -го элемента, a_j – радиус провода j -го элемен-

**

= ⁽ r i , ki - r j , kj ( l )) B a ⁽ r i , ki, ^rj , kj ( l ))

5 i = i g ( r * ki ) E ⁽ in ) ( r i * ki );

i , j = 1,_, N ,    k i = 1,_, N i ,

^А j/2 .

^-А j /2’

k j = 1,^, N j .

3. Геометрия метаструктуры

Общий вид геометрии исследуемой метаструктуры представлен на рис. 2, а . Здесь D – максимальный размер элементов структуры; l_x , l_y , – расстояние между геометрическими центрами соседних элементов вдоль осей x и y ;

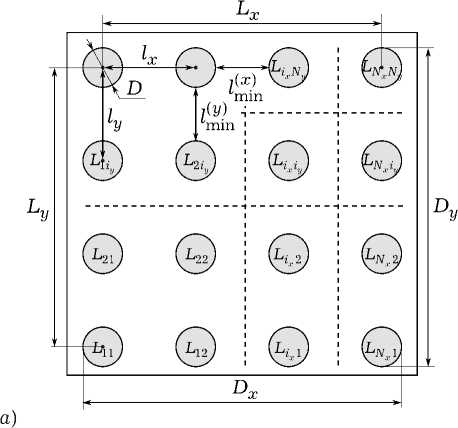
Рис. 2. Геометрия метаструктуры: а ) общий вид метаструктуры; б ) геометрия элементов L_{i i} xy

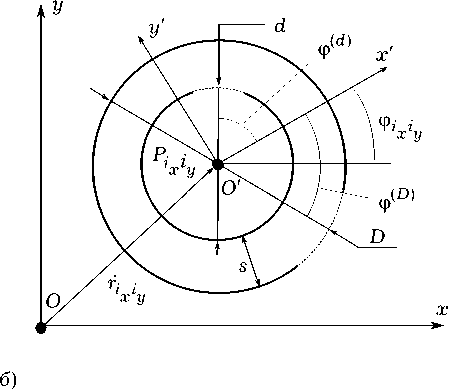
L_x , L_y , – суммарные расстояния между геометрическими элементами вдоль осей x и y . Геометрические центры элементов расположены в

точках P = {x ,y ,h}, где i , i xy x y точек, i = 1,..., N , i = 1,..., N , h x     xy     y

–

индексы

–

высота

расположения метаструктуры над плоскостью xOy . Таким образом, общее число элементов структуры N = N_x × N_y .

Определим некоторые соотношения, связывающие различные параметры структуры, полагая, что ее геометрический центр совмещен с началом координат:

• суммарные расстояния:

Элементы, образующие структуру, представляют собой двойные разомкнутые кольца (рис. 2, б ). Здесь D – диаметр внешнего кольца, d – диаметр внутреннего кольца, углы ϕ^{( D )}, ϕ^{( d )} определяют взаимную ориентацию зазоров колец элемента в его собственной системе координат x ′ y ′ z , начало которой O ′ совпадает с точкой P_{i i} .

xy

При построении матрицы СЛАУ используется сквозная нумерация элементов по индексу i = 1,..., N . Переход к сквозной нумерации осуществляется по формуле:

L x = ( N x

-

1) l x , L y =( N y

- 1) l_y ;

• геометрические размеры структуры:

i=i +(i -1)N , xy x ix = 1,..., Nx,   iy = 1,..., Ny.

D = L + D , D = L + D ; xx  yy

• минимальное расстояние между элементами:

( x )                     ( y )

min x ; min y ;

• координаты геометрического центра элементов:

Рассмотрим геометрию элементов более подробно. Уравнение образующей разомкнутого кольца радиуса a с зазором угловой шириной ξ, расположенного на высоте h вдоль оси z , может быть описано радиус-вектором:

x ix

-

y y

-

l x ( N x

2 l_y ( N_y

-

+ ( i_x - 1) l_x ,

-

¹⁾ +( i y

-

1) l_y .

В качестве исходных брать N , N , D , l и xy  x ровку к длине волны.

параметров можно вы- l_y , осуществляя норми-

Геометрия элементов Li i , образующих ме-xy таструктуру, представлена на рис. 2, б. Каждой точке Pi i поставлен в соответствие радиус-век-xy тор Г i ‘и угол Ф; i , определяющий ориента-ixiy              ixiy цию элемента Li i в плоскости xOy глобальной xy системы координат. Если ϕi i выбирается слу-xy чайно, то структура является киральной.

T(t) = a costxo + a sinty + hZo, t ∈[-π+ξ/2,π-ξ/2].

Осуществим репараметризацию данного уравнения. Натуральный параметр на разомкнутом кольце определяется как интеграл:

t

l(t) = J | T(t ‘) | dt' = at, где

T      drT(t)           T          T T l (t) =       = -a sint x + a cost y + hz , dt

– касательный вектор к образующей. Таким образом, в натуральном параметре уравнение разомкнутого кольца будет иметь следующий вид:

r ( l ) = a cos( l / a ) X g + a sin( l / a ) i / g + 0 z g , l e [ a (—n + ^ /2), a (n — ^ /2)],

Линейная длина разомкнутого кольца составляет L a = 2(n — £) a . Линейная ширина зазора d ^ = 2 a sin(^ / 2).

Таким образом, для элемента L_j , состоящего из двух разомкнутых колец L ⁽ _j ^{D )} и L ⁽ _j ^{d )}, можно записать:

ii

r(i)(l) = — cos(2l / i)xо + — sin(2l / i)yg + 0zg, l e 2[(—n+ ^(i)/2),(n —^(i) / 2)], i = D,d.

Под ^^{( D} ) , ^⁽ d ) будем понимать угловую ширину зазоров соответствующих колец. В дальнейшем

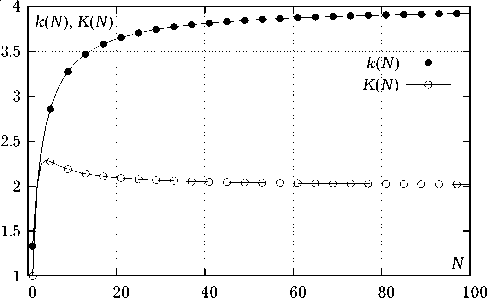
Рис. 3. Графики относительной скорости расчетов

кольцо диаметра D будем называть D а диаметра d – d -кольцом.

Для поворота элемента на угол ф; ;

i _xi_y

мо умножить матрицу поворота

г?

R ixiy

( cos(p i i ) xy

—

V

sin(Qj i ) xy

sin(Pi i ) xy cos(Qi i ) xy

-кольцом,

необходи-

на исходный вектор

r (i ) ( l ), i = D , d , а

для пере-

мещения структуры в точку P_{i i} – прибавить к x У     _

полученному вектору радиус-вектор r .

x y / ( i )

Таким образом, радиус-векторы r_{i i}

( l ),

i = D , d , описывающие образующие элемента,

помещенного в точку Pi i xy угол ф; j , можно записать в ixiy

и повернутого на виде

ставляет N ⁽¹⁾ = ( N i + N j )². Матрицы собственных импедансов в случае разомкнутых колец можно построить по элементам первой строки. Если ■v²i ) — вектор, содержащий элементы первой строки собственной матрицы импедансов i -кольца, то элементы матриц z _ii определяются выражением:

z lm = v\ m — 1 | + 1 , ^l , m = 1, . , ^Ni .

Таким образом, число существенных элементов матрицы собственных импедансов составит

N ⁽²⁾ =( Nd + N d ) + 2( NdN ).

Если кольца разбиты на сегменты равной длины, то справедливо тождество:

D d^{T z} d ( z D ) .

В этом случае число существенных элементов составит

r(i\ (l) = R i ixiy          i

.i ? ⁽ i ) ( l )+ r i i ,

xy

xy

i = D , d .

Это выражение используется для определения матриц z _ij после перехода к сквозной нумерации по формулам (16).

4. Алгоритм расчета матриц импедансов

Определим возможности минимизации вычислительных затрат при определении матриц собственных и взаимных импедансов. Рассмотрим собственную матрицу элемента, образующего структуру. Она имеет вид

2 _ z ii =

здесь

D z D i D

V z d г j zi

d z D

d z d 7

,

матрицы взаимных импедансов i - и

yx • i j-кольца размерностью Ni х Nj; z i

–

матрица

собственных импедансов i -кольца размерностью

N i х N i . Общее число элементов матрицы z ii со-

N ⁽³⁾ =( Nd + N d ) + ( Nd^ ).

Обозначим через k (i ) = N ⁽ i ) / N ⁽ j ) , j = 1,2,... относительную скорость вычисления матрицы собственных импедансов. Тогда при Nd , N d ^ 1 k ⁽²⁾ ^ 2, k ⁽³⁾ ^ 4, т. е. скорость вычислений матрицы собственных импедансов z _ii возрастает соответственно в 2 и 4 раза.

Перейдем теперь к определению элементов z ij общей матрицы СЛАУ. В общем случае число элементов z ij составляет N e1 = N ², где J — число излучающих элементов в структуре. В случае киральной среды, состоящей из одинаковых элементов, матрицы их собственных импедансов

УХ            УХ

УХ            УХ

будут равны z _ij = z _e , а в силу взаимности z _ij = z _ji и число существенных элементов определится как

N e ² = N ( N — 1)/ 2 + 1.

Введем обозначения k = k ₁⁽³⁾, K = N_e ⁽²⁾ / N_e ⁽¹⁾. На рис. 3 представлены относительные скорости

Cl)

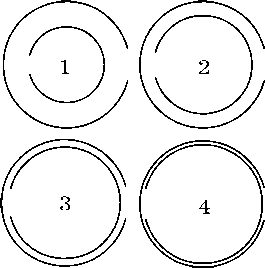
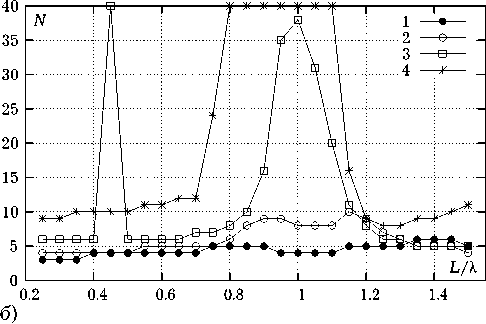
Рис. 4. Геометрия элементов метаструктуры с различным соотношением S / L (1 – S / L = 0.08; 2 – S / L = 0.04; 3 –

S / L = 0.02; 4 — S / L = 0.01) и результаты оценки сходимости итерационного процесса при различных соотношениях L / X для этих элементов

расчетов матрицы собственных импедансов и общей матрицы СЛАУ.

5. Результаты численного моделирования

Численное моделирование осуществлялось в два этапа:

• •    Определение сходимости итерационного процесса при расчете внутреннего взаимодействия между кольцами одиночного элемента;

• •    Определение сходимости итерационного процесса при расчете взаимодействия между элементами метаструктуры в случае их хаотической ориентации.

Возбуждение структур осуществлялось плоской линейно поляризованной электромагнитной волной (ПЭМВ), электрический вектор которой можно записать следующим образом:

E ⁽ in ) ( r) = p o E о exp(— ik e r + y), где к = k o k — волновой вектор; к о — единичный волновой вектор; k – волновое число; E ₀ – амплитуда волны; p o — единичный вектор поляризации; у — начальная фаза. Преполагалось, что E o = 1 В/м, у = 0, P o = x o , к о = - Z o (волна падает против оси Oz ).

Критерий оценки сходимости результата строился в соответствии с неравенством:

б <  5 к

max j

(t j +”- j4 )

^e ( к + 1) i_j

7 ( к )

где i_j – вектор значений токов на сегментах j -го элемента структуры при k -й итерации. В качестве величины, иллюстрирующей сходимость, была выбрана величина:

С к =

1+^ ’

стремящаяся к 1 при 5 к ^ 0. Число б в расчетах

- 3 полагалось равным 10 .

Одиночный элемент. Выбор первичных параметров, определяющих геометрию одиночного элемента, осуществлялся с учетом приоритетного значения их физического смысла. Таковыми являются:

• •    средняя длина кольца L = п( D + d ) — определяет резонансные длины волн системы при ^⁽ d ) ^ 0 и ^⁽ D ) ^ 0;

• •    расстояние между кольцами S = ( D — d ) / 2 — определяет общую добротность резонансов системы и степень взаимодействия колец;

• •    угловая ширина зазоров d - и D -колец ^⁽ d ) и ^⁽ D ) - определяет добротность собственных резонансов соответствующих колец;

• •    ориентационные углы d - и D -колец ф⁽ d ) и ( D )

ф — определяют степень пространственной связи с другими элементами системы;

• •    число сегментов d - и D -колец N_d и N_D .

Остальные параметры можно получить из первичных параметров. Для всех численных экспериментов считались постоянными следующие параметры: ф⁽ d ) = п, ф⁽ D ) = 0, ^⁽ d ) = ^⁽ D ) = п /6, N_d = N_D = 50. При исследовании одиночного элемента изменялись отношения S / L и L / X. Результаты оценки сходимости показаны на рис. 4. Из рисунка видно, что число итераций, необходимое для достижения точности, заданной числом б , существенно зависит от отношения S / L . Важным является тот факт, что число итераций резко возрастает для соотношения S / L = 0.02 в окрестности значений L / X, соответствующих полуволновому и волновому резонансам колец. В среднем число итераций для элементов с соотношением S / L ^ 0.04 лежит в пределах от 3 до 10. Для системы колец с соот-

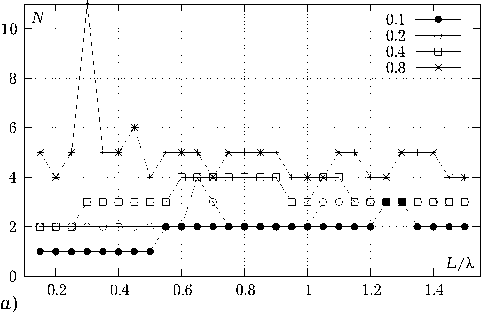
Рис. 5. Результаты оценки сходимости итерационного процесса при различных соотношениях D / l в зависимости от l / X для системы 2 х 2 элемента ( а ) и графики сходимости для наихудшего случая ( D / l = 0.8, l / X = 0.3) при увеличении числа элементов N x х N y ( б )

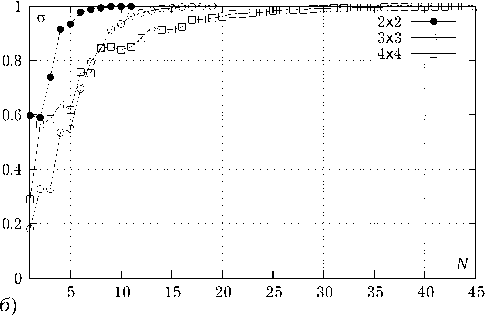
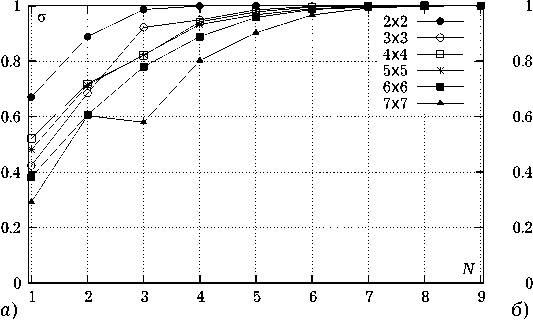
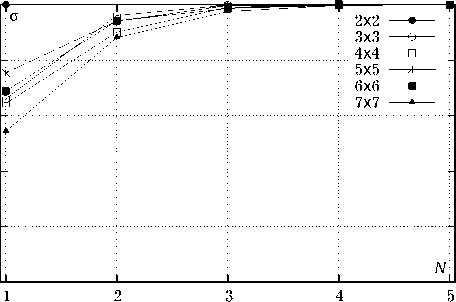
Рис. 6. Результаты оценки сходимости итерационного процесса при при увеличении числа элементов N x х N y в системе: а ) D / l = 0.8, l / X = 0.35; б ) D / l = 0.4, l / X = 0.3

ношением S / L = 0.01 сходимость итерационного процесса в окрестности волнового резонанса отсутствует.

Таким образом, применение метода Гаусса – Зейделя непосредственно к системе элементов может быть неэффективным при очень малых значениях S / L , а также вблизи резонансных частот колец, входящих в систему, поэтому здесь более уместными являются аналитические методы решения СЛАУ, т. к. число элементов общей матрицы относительно невелико (в нашем случае матрица имела размерность 100 х 100).

Метаструктура. При моделировании метаструктуры рассматривался случай с хаотической ориентацией элементов. Геометрия элементов задавалась отношением S / D = 0.08, где D – внешний диаметр кольца, привязанный к базовому расстоянию между геометрическими центрами l элементов отношением D / l. Расстояния lx и ly полагались равными l. Остальные параметры были такими же, как и у исследованных ранее одиночных элементов. На рис. 5, а представлены результаты оценки сходимости итерацион- ного процесса для системы 2 х 2 элемента при D / l = 0.1, 0.2, 0.4, 0.8 в диапазоне l / X от 0.15 до 1.5. Видно, что при D /1 ^ 0.4 число итераций не превышает значения 4, при D / l =0.8 (очень плотная упаковка элементов) число итераций имеет максимум при l / X = 0.3, что связано, по всей видимости, с возникновением резонансных явлений в элементах. Далее для этого случая была проведена оценка сходимости итерационного процесса при увеличении числа элементов Nx х Ny в системе (рис. 5, б). Как видно из рисунка, число итераций, необходимых для обеспечения заданной точности, резко возрастает при увеличении числа элементов, что неприемлемо с точки зрения численных расчетов.

Далее на рис. 6, а показан результат оценки сходимости для того же соотношения D / l при l / X = 0.35. Число итераций при увеличении Nx х Ny меняется незначительно (с 5 до 9 при увеличении Nx х Ny с 4 до 49), причем при дальнейшем увеличении числа элементов прирост числа итераций уменьшается. Можно предположить, что дальнейшее увеличение числа элементов приведет к некоторому предельному значению N.

На рис. 6, б показаны графики, иллюстрирующие сходимость итерационного процесса для системы элементов с отношением D / l = 0.4 (средняя плотность упаковки элементов) при l / λ = 0.3. В данном случае для достижения требуемой точности необходимо от 1 до 5 итераций, и здесь также наблюдается стремление N к некоторому пороговому значению, причем оно в два раза меньше, чем в случае, представленном на рис. 6, а .

Графики, представленные на рис. 6, кроме иллюстрации процесса сходимости, позволяют также оценить степень взаимной связи элементов системы. Так, чем дальше значение σ от единицы при N = 1, тем сильнее межэлементная связь. Таким образом, количественную оценку степени взаимодействия элементов v в процентах можно рассчитать по формуле v = (1-σ1)×100. (17)

Заключение

Таким образом, в статье представлена математическая модель метаструктуры, представляющей собой слой элементов, состоящих из двойных разомкнутых колец. В рамках данной модели произвольным может быть число элементов, их ориентация, а также диаметры и зазоры колец. В качестве основы для учета взаимодействия предложена модификация метода Гаусса – Зейделя, где базовыми являются матрицы собственных и взаимных импедансов элементов метаструктуры. Приведен алгоритм быстрого расчета матриц.

Оценка эффективности метода проведена как для метаструктры, так и для одиночного элемента в случае решения задачи дифракции (падение плоской линейно поляризованной электромагнитной волны против оси Oz с поляризацией в направлении оси Ox ).

Результаты моделирования для одиночного элемента показали, что для близкого расположения колец с малым зазором метод может быть малоэффективен, а вблизи резонансных длин волн даже неприменим. В случае достаточной разности диаметров колец эффективность метода резко возрастает.

По результатам моделирования метаструктуры можно сделать следующие выводы:

• •    метод эффективен даже в случае большой плотности упаковки элементов D / l ≈ 0.8, за ис-

• ключением тех частот, на которых наблюдаются резонансные явления в элементах, образующих метаструктуру;

• •    при увеличении числа элементов число итераций при заданной точности стремится к некоторому предельному значению, и это предельное значение будет тем ниже, чем ниже требуемая точность и отношение размеров элементов к расстоянию между ними.

Следует отметить, что рассмотренные в статье случаи являются достаточно экстремальными, так как для структур, наиболее часто рассматриваемых в литературе, отношение размеров элементов к расстоянию между ними является гораздо меньшим. То же касается отношения размеров элементов к длине волны.

Предложенная методика имеет большие возможности в сравнении с феноменологической теорией и может быть использована, например, для моделирования процессов в фотонных кристаллах. Отметим также, что она позволяет оценить степень межэлементного взаимодействия.