Расчет зеркал для формирования заданных диаграмм направленности

Задача формирования заданной диаграммы направленности (ДН) в оптическом диапазоне является актуальной для широкого круга прикладных задач лазерной обработки материалов, оптической связи, светотехники. В работе [1] проведен расчет поверхности зеркала для фокусировки в заданную кривую в пространстве. Расчет зеркала в [1] проведен в приближении геометрической оптики. Метод работы [1] не применим к расчету зеркал для формирования двумерных диаграмм направленности (ДН). В работах [2-4] в приближении геометрической оптики рассмотрены методы расчета отражающих и преломляющих дифракционных оптических элементов для фокусировки в заданные кривые и двумерные области. На взгляд авторов, методы работ [2-4] ограничены параксиальными областями и не могут быть адаптированы к задаче расчета зеркальных поверхностей. Задача расчета зеркальной поверхности имеет свои особенности и ряд специфических свойств, анализу которых и посвящена настоящая работа.

Общий вид зеркальной поверхности для формирования заданной ДН

Рассмотрим расчет поверхности зеркала для формирования заданной ДН при сферическом освещающем пучке. Поверхность зеркала представим в параметрическом виде

M ( ст , у ) = ( х ( ст , у ), у ( ст , у ), z ( ст , у )) ,            ⁽¹⁾

ками поверхности зеркала и углами, определяющи- ми отраженные лучи.

Единичный вектор нормали к поверхности зер кала имеет вид:

9М(ст,у)х 9М(ст,у) п(ст,у)= дст        ду дМ(ст,у) дМ(ст,у) дст        ду

Предполагая, что центр освещающего сферического пучка расположен в начале координат, запишем закон отражения в векторной форме:

а ( ст , у ) = а о ( ст , у ) - 2 п ( ст , у )( а 0 ( ст , у ) , п ( ст , у )) , (4)

где а ₀ ( ст , у ) = М ( ст , у ) / |м ( ст , у)| - единичный вектор падающего луча, а ( ст , у ) - единичный вектор отраженного луча. Полагая в (4) а ( ст , у ) = р ( ст , у ) , получим систему 3-х дифференциальных уравнений в частных производных для расчета поверхности зеркала М ( ст , у ) :

р ( ст , у ) = а о ( ст , у ) - 2 п ( ст , у )( а о ( ст , у ), п ( ст , у )) . (5)

Система дифференциальных уравнений (5) может быть сведена к следующим двум уравнениям

Г р ( « , г)^'^Л" ^{ст 1} а о Ы^{/ М 1ст} <’■ V дст У V дст У ( р ( ст , у ) ' M - ' а Ы 5 М ( 2 : 1 ) 1.

V ду У V ду У где x,y,z - декартовы координаты. Заданную ДН определим через единичный вектор

' р ⁽ ст , у ) =

V

Рх (ст,уГРу (ст,У)Pz G^L

'- СО5 ⁽ р ^(ст , у ⁾⁾ - 51п ⁽ Ц ^(ст , у ⁾⁾" sin ( p ( ст , y ))

V cos ( p ( ст , y )) cos ( ц ( ст , y )) ,

Легко видеть, что уравнения (6) являются соотношениями полосы для уравнения эйконала. Таким образом, расчет поверхности М ( ст , у ) сводится к решению системы (6). Непосредственной подстановкой можно убедиться, что решение системы (6) имеет вид:

представляющий направление отраженных от зеркала лучей через углы ц и р . При этом ц есть угол между проекцией вектора р ( ст , у ) на плоскость XOZ и оптической осью (осью Oz ), а в - угол между вектором р ( ст , у ) и плоскостью XOZ . Функции ц ( ст , у ) , Р ( ст , у ) описывают лучевое соответствие между точ

|М| - ( р ( ст , у ), М ) = 2 f ( ст , у ) Г ^д р ^{(ст ,} у ) M ) 2 ^д f ^{(ст ,} у ) V дст , У дст , f ^д р ^{(ст ,} у ) M ) =— ₂ ^д f ^{(ст ,} у ) V ду , У ду ,

где M = ( x , y , z ) . Уравнения (7) определяют поверхность (1) в неявном виде. Первое уравнение в (7) представляет параболоид вращения с фокусом f (ct , y) и осью p ( c , y ) . Второе и третье уравнения в (7) являются частными производными по ст и у первого уравнения. Поэтому поверхность (7) является огибающей двухпараметрического семейства параболоидов вращения с фокусами f ( ст , у ) . В частном случае р ( ст , у ) = р ( у ) , когда диаграмма направленности соответствует линии, поверхность зеркала (1) является огибающей однопараметрического семейства параболоидов с фокусами f ( у ) .

Следует отметить, что далеко не при всяком выборе гладких функций ц ( ст , у ) , в ( ст , у ) , f ( ст , у ) можно получить решение исходной задачи, соответствующее гладкой поверхности без самопересечений и областей геометрической тени. Решение (7) следует рассматривать лишь как отправную точку при конструировании сложной поверхности.

В последующем изложении авторы попытаются дать несколько полезных рекомендаций при расчете зеркал для формирования наиболее практически интересных ДН, соответствующих отрезку и прямоугольнику.

Расчет поверхности зеркала для формирования ДН в виде отрезка

При формировании ДН в виде отрезка в плоскости XOZ , направления отраженных лучей

p ⁽ y ⁾ = ⁽ — sin ⁽ p ⁽ y ⁾⁾, 0,cos ⁽ p ⁽ y ⁾⁾⁾,

це [ ц

min , ^ max

1 У ^е[ У min , Y max ]

зависят только от одного параметра у , где ц(у) -угол, составленный отраженным лучом с оптической осью (осью z ). В этом случае система (7) принимает вид

[ Ml-(р(у),М)=2 f (у),

1Г dрСу) m L2 df (Y). (9) [_( dу , ) dу

Хотя функция f (у) однозначно определяет все характеристики зеркала, однако, с точки зрения инженера-расчетчика, выбор параметра у и функции f (у) из условия контроля энергетических характеристик формируемого пучка и геометрических параметров зеркала является трудной задачей. Предлагается расчет трехмерной поверхности зеркала проводить через расчет цилиндрического профиля для фокусировки в отрезок, являющегося центральным сечением зеркала. В качестве параметра у предлагается использовать угол, составленный падающим лучом в плоскости XOZ c осью z. Данный выбор позволяет заменить определение функции f (у) выбором функции лучевого соответствия ц(у), имеющей яс- ный физический смысл и позволяющей контролировать геометрию зеркала и энергетику формируемого пучка.

Расчет цилиндрического профиля из условия формирования заданной функции лучевого соответствия ц(у) является тривиальной задачей и сводится к вычислению следующего интеграла [5, 6]:

Г r (Y)= ro-exp

А

6 ,

V^Y min ^ye[y min , ^y max ^]

где r(у) - радиус вектор точки цилиндрического профиля, а углы уmin,ymax определяют угол охвата пучка.

Требуя, чтобы каждый параболоид в (9) содержал соответствующую точку профиля (10), несложно получить функцию f ( у ) в виде:

f (у)= r(y)-cos2 ^Y ^(у)^ .

Уравнения (9)-(11) полностью определяют поверхность зеркала, при этом контроль энергетических параметров формируемого пучка осуществляется функцией ц(у).

Расчет поверхности зеркала для формирования двумерной ДН

Рассмотрим расчет поверхности зеркала для формирования двумерной ДН. В этом случае расчет поверхности зеркала также предлагается проводить с использованием цилиндрического профиля для фокусировки в отрезок, определяющий размер ДН ц ( у ) е [ ц _min, p _max ] в плоскости XOZ . Параметр ye [ y _min, Y max ] , как и ранее, есть угол, составленный падающим лучом в плоскости XOZ с осью z . Двумерную ДН предлагается строить из отрезков, так что при фиксированном параметре y=y _о лучи, отраженные от кривой

^{м (ст ,} У о ) = ^{( x (ст ,} У о ) У ^{(ст ,} У о ) , z ^{(ст ,} У о ))

на поверхности зеркала, формируют отрезок

Р ^{(ст ,} у ) =

г_cos(p(ст,yо ))sin(u(yо )Г sin(P(ст,y о))х cos(в(ст,yо )cos(y(yо )),

где Р ^{(ст ,} У О Homn ⁽ У о ^{) , ст} max ⁽ У О ^)] - ^{Углы ст} min ⁽ У О ) , ст _max (у _о ) определяют поперечный размер ДН в плоскости P ( у _о ) :

x-cos(p(y о))+z-sin(^(y о ))=О -

Такой выбор построения двумерной ДН позволяет рассматривать поверхность зеркала как семейство кривых M(o,y 0) по параметру Yo, каждая из которых принадлежит поверхности зеркала для формирования ДН в виде отрезка (12). Указанное представление поверхности зеркала полностью согласуется с общим решением (7), где первые два уравнения при y=Y0 определяют зеркало для формирова- ния отрезка, а третье уравнение выделяет кривую на поверхности этого зеркала. Для формирования отрезка (12) предлагается определить параметр о при Y=Y 0 как угол между падающим лучом в центральном сечении P(y 0) зеркала и осью зеркала t^H—srn^Y о Mcos(4(Y о))).

В этом случае функция f (o , y) при Y=Y 0 полностью определяется центральным профилем r (o , y 0 ) - Расчет центрального профиля для формирования отрезка (12) проводится из условия формирования заданной функции лучевого соответствия P(ct , y 0 ) и сводится к вычислению интеграла [5, 6]:

( О

' J    tg I

V ^a m.n ⁽Y 0 )

Г ^(о , Y о ) = r o ⁽Y о ^{) ex}P

^"Pfe Y o )

° ^еЬ_т.„ ⁽Y 0 ). ^ max ⁽Y 0 ^{) ]}

Параметры ст _mi „ (y ₀ ) , о _max ( Y о ) в (13) позволяют контролировать поперечный размер зеркала, а параметр г _о (y о ) выбирается из условия прохождения кривой M (ct , y о ) через соответствующую точку центрального профиля ⁽ r ⁽y о ) si„ ⁽ Y о ) ^о,^- r ⁽ Y о ) c^{os (} Y о )) -

Требуя, чтобы каждый параболоид в (9) содержал соответствующие точки профиля (10) и зеркала для формирования отрезка (12), несложно получить функцию f (ct , y) в виде:

f ⁽ CT , Y ) = r ⁽ Y ) r i (ct , y^{) x}

2 f Y-h(y))   if ct-P(ct,y))      (14)

xcos I -——cos I---I

I 2 J I 2 J

Уравнения (7),(10),(13),(14) полностью определяют поверхность зеркала, при этом контроль энергетических параметров формируемого пучка в продольном направлении (вдоль оси Ox ) осуществляется функцией ^(y), а в поперечном направлении (вдоль оси Oy ) — функцией P(ct , y) -

Рассмотренный метод был использован для расчета зеркала для формирования симметричной прямоугольной ДН ц е [ — 4о^о,4о^о ], р е [ - 2о^о,2о^о ] - На рис. 1 показана рассчитанная поверхность зеркала. Напомним, что оптическая ось зеркала совпадает с осью Oz , а точечный источник света находится в начале координат. На рис. 2 приведена сформированная зеркалом диаграмма лучей, где вдоль осей Ox,

Oy показаны расчетные значения углов ц и р . Для расчета углов ц , р производился численный расчет вектора нормали к поверхности зеркала, а затем по закону Снелиуса (4) рассчитывались отраженные лучи. Расчетная форма диаграммы полностью соответствует заданным функциям лучевого соответствия Ц ⁽ Y ⁾ ~ Y 2 , Р ⁽ о^ ) ~ ст ² и показывает формирование прямоугольной ДН с заданными размерами.

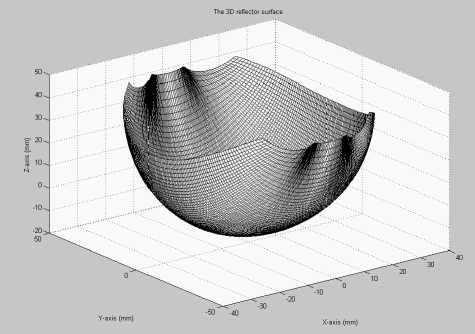
Рис. 1. Поверхность зеркала для формирования прямоугольной ДН с размером 8о^о х 4о^о

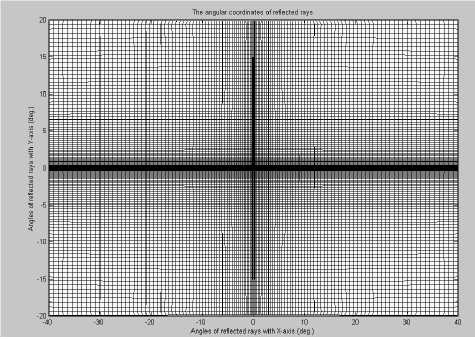
Рис. 2. Угловые координаты отраженных лучей

Области применения метода

Рассмотренный метод может быть легко модифицирован на случай расчета поверхности зеркала для фокусировки заданную двумерную область в плоскости z=f. Определим область фокусировки при z=f через функции лучевого соответствия в виде f x(Y)e[xmm,xmax ]> )

^{X (o ,} Y ) = |                            I ,               ⁽¹⁵⁾

( y (CT,Y)e[y min, У max (Y)]J

Повторяя рассуждения, использованные при получении решения (7), несложного получить общее представление поверхности зеркала в виде огибающей двухпараметрического семейства эллипсоидов вращения

I M| +1 X ( g , y ) - M| =v ( g , y )

Г 5 X ( g , y ) ( x ( g , y ) - M ) ) = 5^ ( g , y ) ^ 8g , |x( g , y ) - M| J     8g

Mx⁽G , Y ) ⁽ X ⁽G , Y ) — M ) J= d9⁽G , Y )

_v 8y ^, |X ( g , y ) - M| ^J     8y ’

где функция q(g , y) является длиной большой оси эллипсоидов и представляет распределение эйконала в области фокусировки. Отметим, что первый фокус совпадает с источником, а второй фокус – с текущей точкой ( x (y), y (g , y) , / ) области фокусировки. Методология выбора функции q(g , y) полностью совпадает с рассмотренным выбором функции f (g , y) при расчете зеркал для формирования диаграмм направленности в виде отрезка и двумерной области.

Метод также может быть использован для расчета преломляющих оптических элементов. В этом случае в уравнениях (16) достаточно заменить уравнение эллипсоида на уравнение поверхности линзы n'Ml+|x(g,y)-M|=v(g,y) , (17) где n - показатель преломления, обеспечивающей фокусировку лучей от источника в текущей точке области.

Заключение

В работе получено, что зеркальная поверхность для формирования заданной ДН имеет вид огибающей двухпараметрического семейства параболоидов вращения с фокусами f(з,y). Функция f(а,y) определяется по методу представления поверхности зеркала в виде огибающей семейства зеркал для формирования ДН в виде отрезков, которые составляют заданную ДН сложной формы. Выбранный вид параметризации (g,y) удобен для контроля энергетических параметров формируемого пучка и геометрических параметров зеркала. Приведенный пример расчета зеркальной поверхности для формирования прямоугольной ДН показывает хорошую работоспособность метода.

Общее представление поверхности зеркала легко модифицируется на случай расчета отражающей или преломляющей поверхности для фокусировки в заданную двумерную область.