Расчетная модель метрологических характеристик волоконно-оптических измерительных устройств

Актуальны следующие основные задачи метрологических исследований алгоритмов и технологических режимов:

• -    формирование структурной схемы модели для расчета суммарных метрологических характеристик каналов измерительной системы по нормированным погрешностям входящих внешних измерительных компонент;

• -    расчет по модели и исходным нормированным данным суммарных инструментальных погрешностей (границ их интервалов) контроля базовых глубинных параметров волоконнооптического устройства измерения давления и температуры (далее – ВОУИДиТ);

• -    обработка имеющейся статистики по характеристикам для расчета параметров ВОУИДиТ и определение их метрологических показателей, требуемых для дальнейших вычислений;

• -    исследование возможных инструментальных (аппаратных) погрешностей (границ их интервалов) алгоритмов вычисления (моделирования) давления и температуры, а также снижения погрешности, принятие ряда исходных величин с помощью экспертной оценки.

В результате должна быть выведена предварительная оценка основных метрологических характеристик ВОУИДиТ применительно к его базовым алгоритмам снижения погрешности, что является целью данных метрологических исследований.

РАСЧЕТНАЯ МОДЕЛЬ, НОРМИРОВАНИЕ

И ОПРЕДЕЛЕНИЕ РЕЗУЛЬТИРУЮЩИХ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ВОУИДиТ

Для проведения метрологической оценки рассматриваем как базовое ВОУИДиТ для глу-

бинных (внутрискважинных) измерений мульти -сенсорный скважинный инструмент типа МСИ-0 Phoenix фирмы Schlumberger [5] (табл. 1).

Расчетную модель измерительную схему (далее - ИС) для метрологических исследований на основе ГОСТ Р 8.596-2002 целесообразно представить в виде схемы на рис. 1. Типовая ИС содержит сложный измерительный канал ИС, образуемый измерительным компонентом (датчиком и преобразователем соответствующего параметра), связующим компонентом (каналом передачи данных по силовому кабелю от измерительного компонента на поверхность в АСУТП) и вычислительным компонентом (контроллером сложного ИК-средства контроля глубинных параметров). Данный сложный канал является готовым внешним изделием, используемым для ввода измерительной информации.

В составе схемы модели выделяется комплексный компонент ИС, образуемый связующим и вспомогательным компонентами. Связующий компонент представляет радиоканал передачи данных с контроллера сложного ИК (мультисен-сорный скважинный инструмент типа МСИ-0), расположенного в СУ УЭЦН (системе управления электроцентробежным насосом) скважины кустовой площадки, на АРМ (автоматизированном рабочем месте), расположенном в диспетчерской ЦДНГ (цеха добычи нефти и газа).

АРМ согласно ГОСТ Р 8.596-2002 является вспомогательным компонентом ИС, обеспечивающим нормальное функционирование ИС в части визуализации (отображения) физических значений контролируемых параметров.

Для определения результирующих обобщенных метрологических характеристик каналов ИС введем ряд априорных допущений и условий в соответствии с РД 153-340-11.201-97 «Методика определения обобщенных метрологических характеристик измерительных каналов АСУТП. РАО «ЕЭС России»:

• -    погрешности ИС являются случайными величинами, распределенными по закону

  
  
  

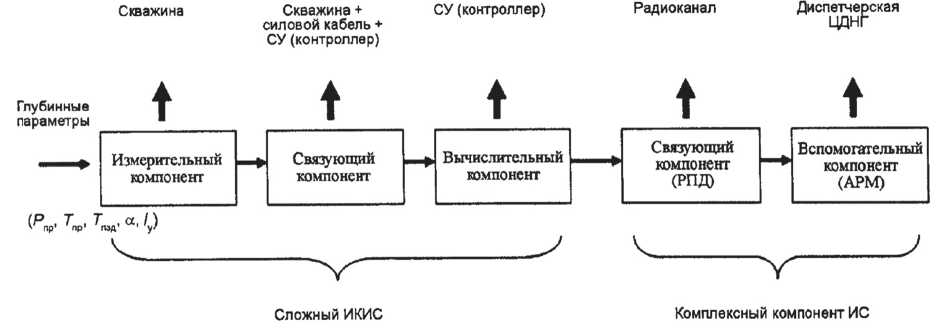
Рис. 1. Структурная схема расчетной модели погрешности ИС

Таблица 1. Виды метрологических характеристик сложного измерительного канала

Вид сложного измерительного канала Нормируемые метрологические характеристики сложного измерительного канала Измеряемые параметры Диапазон измерения Предел допускаемой основной приведенной погрешности Мультисенсорный скважинный инструмент Phoenix (тип МСИ-0) Давление 0…35 МПа 0,1 Температура 0…150°С 1,0 равномерной плотности, т. е. внутри интервала, ограниченного предельными значениями погрешностей;

• -    все значения погрешностей равновероятны;

• -    доверительную вероятность контроля принимаем Р = 0,95.

Тогда, согласно РД 153-340-11.201-97, нижняя и верхняя границы интервала, в котором с вероятностью Р = 0,95 находится суммарная погрешность δ для реальных условий эксплуатации (допускаемый предел) определяется по формуле:

5 = ±1,96( 0 " [ A i² + <жк² )/2,        (1)

где σ _кк– среднее квадратическое отклонение (СКО) основной приведенной погрешности комплексного компонента ИС;

Δi – предел систематической составляющей основной погрешности.

Данная погрешность в силу особенностей цифровой передачи и обработки измерительного канала относится к ничтожно малой погрешности, и ею можно пренебречь.

В соответствии с РД 153-340-11.201-97:

[ A i ] = A iV3 .

Тогда

5 =± 1,96/1,73* A ³ *± 1,13 A i .     (2)

Рассчитанные по формуле (2) округленные значения δ , приведены в табл. 2.

Следует отметить, что они носят максимально возможный (предельный) характер для данного типа блока погружной телеметрии.

Обработка осуществлялась для 2 параметров применительно к ВОУИДиТ.

В качестве задач обработки приняты:

• -    выборка предельных (минимаксных) значений параметров;

• -    определение математических ожиданий параметров;

• -    определение дисперсий и средних квадратических отклонений.

Для исключения данных по остановленным скважинам из массива данных скважинного фонда ЦДНГ, определения диапазонов изменения параметров, их математических ожиданий и стандартных отклонений использовался программный пакет Statistica 6.0. Результаты обработки представлены в табл. 3, в которой также указаны полученные значения приведенных (относительных) частных производных, рассчитанных с помощью пакета Mathcad 14. Принятые для Mathcad обозначения параметров и формулы вычислений приведены в табл. 3.

Частные производные (коэффициенты влияния) в формуле расчета погрешности измерения рассчитывались с использованием пакета Mathcad 14.

Таблица 2. Рассчитанные значения суммарных погрешностей для реальных условий эксплуатации

Значение	Параметры
	Pпр	Тпр	Tпэд	α	Iу
±δ , %	0,13	2,13	2,13	2,13	0,06

Таблица 3. Результаты обработки данных

Параметры	Глубина верхних дыр перфорации Hвд, м	Глубина спуска телеметрии Hсп, м	Удлинение верхних дыр, Удлвд, м	Плотность нефти ρнп, г/см3	Обводненность В, %	Затрубное давление Pзат, кгс/см2	Pпр*, кгс/см2
Минимальное значение Pimin	2440,00	200,00	0,00	0,83	1,00	0,10	40,00
Минимальное значение Pimax	3523,00	3163,00	789,90	0,85	99,00	23,00	140,00
Математическое ожидание Mi	2696,15	1866,12	173,70	0,84	57,28	6,30	3,84
Приведенная величина Mi/xmax	0,77	0,59	0,22	0,99	0,58	0,17	0,17
Приведенная ** частная производная формулы для Pз (коэффициент влияния Kl)	δPз/ δНвд= 0,0792	δPз/ δНсп=-0,07	δPз/ δУдлвд= -0,02	δPз/ δРнп=0,01	δPз/ δВ=0,01	-	-
Приведенная ** (относительная) частная производная формулы для Нд (коэффициент влияния Kl)	δHд/ δНвд=0,50	δНд/ δНсп=0,56	δНд/ δУдлвд= -0,02	δНд/ δPнп= -0,31	-	δНд/ δРзат= 0,82	δНд/ δРпр= -0,82

ИССЛЕДОВАНИЕ АЛГОРИТМА РАСЧЕТА ПОГРЕШНОСТИ ИЗМЕРЕНИЯ

Целью метрологических исследований алгоритма является оценка аппаратной погрешности реализации алгоритма в ИПТК (интеллектуальном программно-техническом комплексе). Методическая погрешность в данном исследовании не рассматривается, так как базовые расчетные зависимости выдаются заказчиком на корпоративном уровне.

В соответствии с РД 153-34.0-11.20-97 среднее квадратическое отклонение случайной составляющей инструментальной погрешности реализации алгоритма расчета погрешности Р₃ может быть оценено по формуле:

» [ S p3 ] = ^{( к}вд2 ^{е 2} ВД ^{+ К}СП² ^ 2 СП ^{+ к}уд.вд2 ^е 2уд.вд +- )

1/2          (3)

|- ^{+ к} Ри > ² Р ип ^{+ к} Р 2 ^{е 2} Р В ^{+ к} В 2 ^{е 2} ) ^{+ о Р}пр ’

\                                 В J где К – коэффициенты влияния соответствующих характеристиик (частные производные), ст - СКО основной приведенной погрешности комплексного компонента ИС.

Нижняя и верхняя границы интервала, в котором находится инструментальная суммарная погрешность алгоритма, согласно РД 153-34.011.20-97 оцениваются по формуле:

5 А [ ^рз] = ± 1,96 а^Зр_з .

СКО инструментальных приведенных

Таблица 4. Рассчитанные значения среднеквадратических отклонений

Значение Параметры Нвд Ноп Удл.вд ρИП B ρ3 Pзат σi, % σВд=5,0 σсн=5,0 σудвд=5,0 σρип=10 σ3=10 σρ=10 σPзат=2,0 погрешностей, вводимых для расчета Р3 параметров, оценивались экспертным путем (табл. 4).

Таким образом,                              1.

a[3P3 ] = ( 0,08252 +(-0,069)2 52 +... )

( ...+(-0,22)252 +0,012102 +0,012102 'j/2 + 0,2 = 0,72%,

J A[ P , ] = ±1,96 • 0,72 = ±1,4157% -1,42%.

ВЫВОДЫ

Проведено расчетное моделирование в со- 3. ответствии с положениями и рекомендациями метрологических нормативно-технических документов.

В результате исследований в рамках принятых допущений, моделей и располагаемой 4. статистики получены приближенные оценки нижних и верхних границ интервалов, в которых с вероятностью 0,95 находятся суммарные инструментальные (аппаратные) погрешности: 5.

• -    контроля глубинных скважинных параметров на примере мультисенсорного скважинного 6. инструмента Phoenix (типа МСО-О), в частности, по давлению на приеме установки электроцен-тробежного насоса ±0,13 %;

• -    алгоритма расчета забойного давления ±1,42 %.

Предложенная расчетная методика метро- 7. логического исследования и обработки статистических данных со скважинного фонда позволяет оценить предельные инструментальные погрешности как при применении другого типа скважинной телеметрии, так и для любых других алгоритмов и технологических режимов.