Расчетная модель наклонного сечения изгибаемого железобетонного элемента без поперечной арматуры

на действие поперечных сил [1] в отдельных случаях (балки без поперечного армирования, балки из высокопрочного бетона) существенно завышает прочность наклонных сечений. Следует отметить, что превышение расчетных значений над опытными величинами разрушающих нагрузок носит систематический характер.

Предлагается расчетная модель наклонного сечения изгибаемого железобетонного элемента без поперечной арматуры (рис. 1). Особенностью расчетной модели является выделение в расчетных зависимостях сил зацепления в наклонной трещине как отдельной компоненты в совокупности усилий, обеспечивающих прочность наклонного сечения при расчете на действие поперечной силы. Схема усилий, действующих в наклонном сечении железобетонного элемента, принята в соответствии с [2].

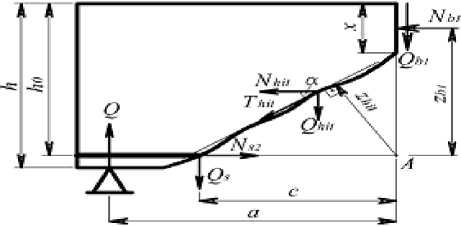
Рис. 1. Расчетная модель наклонного сечения

Принимается, что поперечная сила от приложенной нагрузки воспринимается в наклонном сечении изгибаемого элемента без поперечной арматуры внутренним усилием, которое состоит из следующих компонент: касательного усилия в бетоне сжатой зоны в конце наклонной трещины (Qb1), касательного усилия в продольной растянутой арматуре в начале наклонной трещины (нагельный эффект Qs), вертикальной составляющей усилия зацепления по длине наклонной трещины (Qhit). Тогда условие прочности наклонного сечения изгибаемого элемента на действие поперечной силы запишется в виде:

Q ≤ Q b1 + Q s + Q hit ,                   (1)

Расчетные зависимости составляются из рассмотрения условий равновесия блока над наклонной трещиной (рис. 1). Уравнение равновесия проекций сил на вертикальную ось:

Q = Q b1 + Q s + Q hit ,                   (2)

где Q b1 – касательное усилие в бетоне сжатой зоны над наклонной трещиной; Q s – касательное усилие в продольной растянутой арматуре (нагельный эффект); Q hit – вертикальная составляющая усилия зацепления в наклонной трещине.

Уравнение равновесия проекций сил на горизонтальную ось:

N s2 = N b1 + N hit .                        (3)

Уравнение равновесия моментов сил относительно точки А:

N b1 ×z b1 + T hit ×z hit + Q s ×c = Q×a,       (4)

где N b1 , z b1 – нормальное усилие в бетоне сжатой зоны над наклонной трещиной и плечо этой силы, соответственно; T hit , z hit – усилие зацепления в наклонной трещине и плечо этой силы, соответственно; Q s , c – касательное усилие в продольной растянутой арматуре и плечо этой силы, соответственно; Q, a – поперечная сила и плечо этой силы, соответственно.

В уравнении (4) производим замену:

T hit = Q hit / sinα , z b1 = h 0 (1 – ξ/2) , z hit = с× sinα

Подставляя (2) и (3) в (4), получим:

Q b1 ×a + Q hit × (a – z hit / sinα) +

+ (N hit – N s2 ) × z b1 + Q s × (a – c) = 0   (5)

Горизонтальная составляющая усилия зацепления в наклонной трещине

N hit = Q hit ×ctgα

Усилие Q s определяем в соответствии с предложением С.Н. Карпенко [3]:

Q s = N s2 ×c / h 0 ×γ v = N s2 ×ctgα / 8       (6)

Используем эмпирическую зависимость для определения сил зацепления в трещине, предложенную авторами [4],

τ =

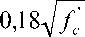
0,31 +

24acrc ag +16

(МПа),

где f_c – цилиндрическая прочность бетона при сжатии (МПа); a crc – ширина раскрытия трещины (мм); a g – максимальный размер крупного заполнителя (мм). Зависимость получена по результатам испытаний бетонных образцов при плосконапряженном состоянии и широко используется в зарубежных исследованиях для установления связи между силами зацепления и шириной раскрытия трещины с учетом размера крупного заполнителя.

Выполнив некоторую модификацию зависимости (7), получим выражение для определения вертикальной проекции усилия зацепления в наклонной трещине:

0,18 Rb* bh о ( 1 - £ )

Q hit =                         .

0,31 +--- c—^ ) a + 16

Величину относительной высоты сжатой зоны бетона над наклонной трещиной ξ находим из уравнения

ξ2 + 2μαξ – 2μαφ = 0, (9)

где μ = А s /bh 0 ; α = E s / E b ; φ = 1 – 0,7 / (100μ + 1).

Ширина раскрытия наклонной трещины a crc в формуле (7) выражается через напряжения в продольной арматуре в начале наклонной трещины σ s2 = N s2 / А s :

a crc = l crc σ s2 / E s . (10)

Касательное усилие в бетоне сжатой зоны над наклонной трещиной Q b1 предлагается определять по нормативной методике [1] с некоторой корректировкой, учитывающей высоту сжатой зоны бетона над наклонной трещиной:

Q b1 = R bt bхω = R bt bh 0 ×ξ²/(1 – ξ). (11)

Подставляя выражения (6), (8), (10), (11) в (5) получим квадратное уравнение относительно σs2. Определив из (5) величину σs2, по формулам (6), (8) и (11) находим значения Qs, Qhit и Qb1, соответственно, которые используются при проверке условия прочности (1). При расчете по предлагаемым зависимостям в первом приближении были приняты некоторые допущения, которые требуют дальнейшего исследования:

• -    угол наклона трещины принят постоянным α = 33⁰ = сonst;

• -    угол наклона трещины совпадает с углом наклона сил зацепления T hit ;

• -    длина проекции наклонной трещины С = 1,5h 0 = сonst;

• -    в формуле (10) принято l crc = 1,5h 0 ; - α = E s / E b = 7 = сonst.

Результаты расчетов по предлагаемым зависимостям (Q cal ), а также их сопоставление с результатами расчетов по нормам США (Q ACI ) и СП 63.13330.2012 (Q СП ) приведены в табл. 1. Для сопоставительного анализа использованы результаты испытаний опытных образцов, опубликованные в [6]. Прочность наклонных сечений по СП 63.13330.2012 [1] определялась по формуле Q b = 0,5R bt bh 0 . Результаты определения прочности наклонных сечений по нормам США (ACI 318) [4] приняты из работы [6].

Таблица 1. Разрушающие нагрузки и расчетные значения прочности наклонных сечений опытных образцов

№	Маркировка балок	b, мм	h0, мм	< , МПа	μ, %	a/h 0	Q exp , кН	Q ACI , кН	Q СП , кН	Q cal , кН	Q exp / Q ACI	Q exp / Q СП	Q exp / Q cal
1	B100	300	925	36,0	1,01	2,92	225	278	378	229	0,81	0,59	0,98
2	B100H	300	925	98,0	1,01	2,92	193	384	523	249	0,50	0,37	0,78
3	B100L	300	925	39,0	1,01	2,92	223	289	394	235	0,77	0,57	0,95
4	BN100	300	925	37,2	0,76	2,92	192	282	385	189	0,68	0,50	1,02
5	BN50	300	450	37,2	0,81	3,00	132	137	187	122	0,96	0,71	1,08
6	BN25	300	225	37,2	0,89	3,00	73	69	94	79	1,06	0,78	0,93
7	BN12	300	110	37,2	0,91	3,07	40	34	46	48	1,19	0,87	0,84
8	BH100	300	925	98,8	0,76	2,92	193	384	523	196	0,50	0,37	0,98
9	BH50	300	450	98,8	0,81	3,00	132	187	255	126	0,70	0,52	1,05
10	BH25	300	225	98,8	0,89	3,00	85	93	127	82	0,91	0,67	1,03
11	BRL100	300	925	94,0	0,50	2,92	163	384	523	146	0,42	0,31	1,12
среднее значение											0,772	0,569	0,978
среднеквадратичеcкое отклонение											0,233	0,170	0,096
коэффициент вариации											30,2%	29,9%	9,8%

Анализ результатов, приведенных в таблице, показывает, что с увеличением высоты образцов и прочности бетона методика расчета, принятая в СП 63.13330.2012 [1], существенно переоценивает прочность наклонных сечений изгибаемых элементов без поперечного армирования. Та же тенденция характерна и для норм США [4], несмотря на имеющиеся в них ограничения, касающиеся абсолютной высоты сечения и прочности бетона. Это позволяет сделать вывод о недостаточном соответствии теоретических предпосылок, заложенных в расчетных моделях и фактическом характере работы наклонных сечений изгибаемых железобетонных элементов. Недостаточное соответствие обусловлено эмпирической природой расчетных зависимостей норм [1, 4] по расчету прочности наклонных сечений. В свою очередь эмпирический характер расчетных зависимостей является закономерным следствием значительных трудностей, возникающих при теоретическом исследовании анизотропного материала (железобетона) при плоском напряженном состоянии.

Выводы: предложенная методика расчета прочности наклонных сечений изгибаемых железобетонных элементов на действие поперечной силы позволяет:

• -    устранить наблюдаемое систематическое превышение расчетных значений над опытными величинами разрушающих нагрузок и обеспечить их лучшую сходимость;

• -    повысить конструктивную безопасность проектных решений, в том числе для элементов из высокопрочного бетона.

• -    на базе физически обоснованной расчетной модели наклонного сечения изгибаемого элемента определить соотношение между компонентами усилий, действующих в наклонном сечении и сократить эмпирическую составляющую расчетных зависимостей.