Расчетная оценка эффекта деформационно-температурного упрочнения арматурной стали класса АТ-1200 (АТ-VII) при предварительном напряжении

Кооперативное взаимодействие системы «нагрузка + время + температура» приводит к изменениям характеристик физико-механических свойств и диаграммы деформирования стали как последствие деформационно-температурного упрочнения и реологических процессов. В данной работе механизм такого взаимодействия исследован на примере термомеханически упрочненной арматурной стали класса Ат-1200 (Ат-VII) [1, 2], являющейся до настоящего времени наиболее высокопрочным из всех отечественных видов стержневой арматуры с условным пределом текучести σ0,2 ≥ 1200 Н/мм2 и временным сопротивлением σu ≥1450 Н/мм2. Наряду с высокой прочностью исследуемая сталь обладает и высокой пла- стичностью – фактическое относительное удлинение δs ≥ 9% и δp ≥2,3%, что существенно выше нормируемых величин.

Опытно-промышленные партии данной арматуры в полном сортаменте (диаметром 10…32 мм) впервые были прокатаны автором на Западно-Сибирском и Криворожском металлургических комбинатах из стали марок 30ХС2 и 30ХГС2.

Среднестатистическая диаграмма условно-мгновенного растяжения стали класса Ат-1200 (Ат-VII) в состоянии поставки как комплексная характеристика ее упруго-пластических свойств приводится на рисунке 1.

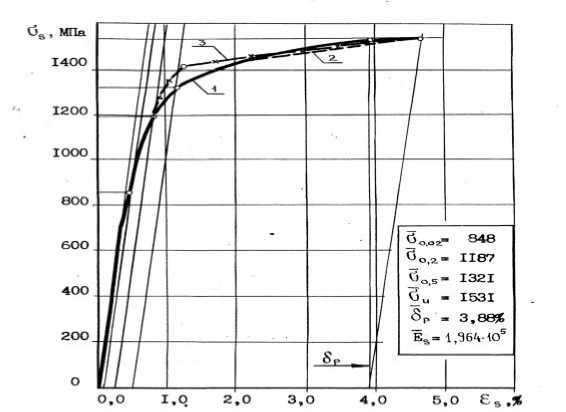
Рис. 1. Среднестатистическая диаграмма растяжения высокопрочной арматурной стали класса Ат-1200 (Ат-VII ): 1 – опытная кривая; 2 - расчетная кривая по уравнениям (4) при 4 узлах интерполяции, соответствующих величинам σel;σ0,2;σ0,5;σu; 3 - расчетная кривая по уравнениям (4) при 3 узлах интерполяции, соответствующих величинам σel; Пσ0,2;σu

На основе обширного экспериментального материала установлено, что при предварительном напряжении наблюдается существенное повышение характеристик сопротивления σ _si ( σ _0,05; σ _0,1; σ _0,2 и т.д.) исследуемой стали малым пластическим деформациям.

Фрагмент результатов испытаний на кратковременное осевое растяжение исходных образцов стали и соответствующих им образцов, подвергнутых предварительному напряжению механическим способом на специальном силовом стенде, а также характерный вид «упрочненной» диаграммы на примере арматуры диаметром 25 мм приводятся в таблицах 1, 2 и на рисунке 2.

Таблица 1 Экспериментальные данные о влиянии предварительного напряжения на прочностные свойства арматурной стали класса Ат-1200 (Ат-VII) диаметром 25 мм

Предварительное напряжение σ sp , Мпа	σ sp sup σ 0,2	Характеристики прочностных свойств, Мпа
		исходные						после выдержки под нагрузкой
		sup σ 0,02	sup σ 0,05	sup σ 0,2	sup σ 0,5	σ sup u	η 1 sup	exp σ 0,02	exp σ 0,05	exp σ 0,2	exp σ 0,5	σ exp u	η 1 exp
564	~0,55	720	846	1047	1161	1345	0,483	824	901	1055	1159	1323	0,608
569		812	932	1097	1206	1360	0,594	839	929	1085	1194	1349	0,611
605		764	891	1105	1257	1423	0,478	879	969	1138	1263	1409	0,600
601		693	881	1105	1240	1403	0,452	835	937	1123	1248	1397	0,552
818	~0,75	779	918	1098	1246	1375	0,556	934	975	1123	1232	1373	0,645
816		622	810	1048	1195	1358	0,388	908	986	1109	1211	1361	0,701
1078	~0,95	873	935	1123	1242	1377	0,547	1140	1174	1228	1275	1375	0,883
1079		783	894	1080	1193	1355	0,538	1132	1212	1259	1282	1380	0,899
1048		829	935	1113	1258	1412	0,566	1134	1166	1223	1298	1412	0,874
1053		723	890	1111	1258	1415	0,464	1101	1148	1226	1306	1430	0,827

Таблица 2

Экспериментальные значения средних относительных приращений характеристик прочностных свойств класса Ат-1200 (Ат-VII) диаметром 25 мм при предварительном напряжении

Характеристики прочностных свойств	Относительные приращения Δ σ = σ i - σ i sup × 100% i        σ i sup при уровнях преднапряжения
	σ sp =0,55 sup σ 0,2	σ sp = 0,75 sup σ 0,2	σ sp =0,95 sup σ 0,2
Δ σ 0,02	13,33	32,94	41,06
Δ σ 0,05	5,32	13,97	28,71
Δ σ 0,2	1,07	4,05	11,54
Δ σ 0,5	~ 0,00	0,11	4,28
Δ σ u	~ 0,00	~ 0,00	~ 0,00

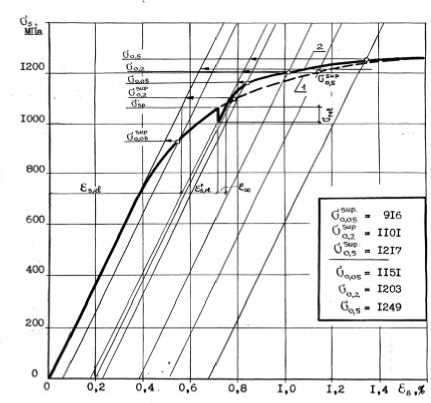
Рис. 2. Изменение диаграммы растяжения высокопрочной арматурной стали класса Ат -1200 (Ат -VII ): 1 – исходная диаграмма; 2 - «упрочненная» диаграмма

Выявленный эффект деформационно-температурного упрочнения носит при этом стабильный и закономерный характер, что позволило обосновать и экспериментально проверить возможность применения расчетного аппарата технической теории упрочнения [3] к арматурной стали класса Ат-1200 (Ат-VII).

Согласно результатам исследований в области теории пластичности и ползучести, современной металофизики и теории прочности металлов пластические деформации относятся к классу термодинамических неравновесных процессов, характеризующихся конечным набором измеряемых макроскопических параметров и «историей» нагружения, и поэтому рассматриваются как диссипативное состояние [4]. На этом основании определение параметров σ _si «упрочненной» в результате преднапряжения диаграммы осуществляется исходя из условия:

∑ ( ε _s,pli + ε _s ^p _{, pli} + ε _sc + ) = f ( σ _s ),                                    (1)

где ε _s ^p _{, pl} - условно-мгновенная пластическая деформация (УМПД) от преднапряжения; ε _{s , pl} - допуск на величину УМПД для искомого параметра σ _s (так, для σ _0,2 ε _{s , pl} = 0,002 и т.п.); ε _sc - деформации ползучести; f ( σ _s ) - функция, описывающая исходную диаграмму УМПД.

При этом совместное влияние длительности действия нагрузки т и температурного воздействия T на параметры диаграммы растяжения стали оцениваются посредством деформаций ползучести e sc .

Деформации ползучести esc при нормальной и повышенных температурах определяют- ся по выражению:

ст

= sc = A -i p

° 0,2 V

г CTsc

—

sup и 0,2

)

B • ( D + lg т ) • (1 + c A Т ),

где ст _sp - величина предварительного напряжения; т - время (ч) выдержки под нагрузкой; с - коэффициент линейного температурного расширения стали равный 0,012 ° C^-1; ЛТ = T i -20 ° C - превышение фактической температуры стали над нормальной; A, B, D – эмпирические коэффициенты для конкретного класса и марки стали.

Очевидно, что важным условием решения задачи в постановке (1) является выбор наиболее корректного способа аналитического описания диаграммы растяжения стали и оценка деформаций ползучести e sc при длительном действии нагрузки.

В рамках данной работы на основе многочисленных результатов испытаний на кратковременное осевое растяжение опытных образцов обоснована возможность использования для аппроксимации диаграммы растяжения стали класса Ат-1200 (Ат-VII) метода, основанного на использовании многоинтервальной (сплайн) интерполяции.

Обзор существующих многочисленных предложений различных авторов показывает, что многие из предлагаемых аппроксимирующих функций не носят универсального характера и могут быть использованы лишь в частном порядке для конкретных видов арматурных сталей. Ряд этих предложений к тому же отличает то обстоятельство, что их авторы стремились к чрезмерной простоте применения предлагаемых зависимостей в практике «ручных» расчетов с использованием минимума экспериментальных данных о механических свойствах стали, вследствие чего неизбежно увеличивается погрешность в приближении расчетных кривых к опытным.

Наиболее предпочтительными из числа рассмотренных являются предложения авторов [3, 5, 6, 7]. Сравнительный анализ этих предложений отображен на рисунке 3 и свидетельствует о более высокой степени приближения по методу сплайн-интерполяции с использованием подхода, принятого в работах [3, 5]. Сравнение опытной и расчетной по данному методу диаграмм исследуемой стали показывает, что на всем диапазоне 0 < стs < сти диаграммы практически совпадают, незначительное расхождение на участке ст0 5 - сти не превышает

1,5%.

В нашем случае функция f (стs), аппроксимирующая исходную диаграмму УМПД, представляется как сплайн-функция общего вида:

f(стs)=Е mi — - п

i=1    Vст 0,2      J где mi, ni, ni - безразмерные параметры сплайна; Ni - номер интервала нелинейной части, на котором оценивается параметр espl; ms^ = —si— относительный уровень загружения стали.

^ст 0,2

Для высокопрочных сталей функция приближения (3) в развернутом виде записывается следующим образом:

, 0 < ° < °

E

° + m 1

° s к ° 0,2

) - П 1 7

” 1

,     ° el <  ° s

< ° 0,2

s s =-

° + m

° s к ° 0,2

) - П 1 7

” 1

+ m 2

° s -к ° 0,2

) П 2 7

” 2

° 0,2 <

° s <  ° 0,5

° + m

° s к ° 0,2

) - П 1 7

” 1

+ m 2

° s - L ° 0,2

) П 2 7

” 2

+ m 3

( ° s l ° 0,2

) - П 3 7

” 3 ,

° 0,5 <  ° s <  ° u

Численный анализ функции (4) показывает, что ее первая f '(ss) и вторая f "(ss) произ водные при ni>2, n2>2, n3>2 непрерывны на всем заданном участке °el - °u. В связи с этим можно утверждать, что в узлах интерполяции слева и справа кривые будут иметь не только общую касательную, но и одинаковую кривизну.

Для высокопрочных сталей к тому же необходимо обеспечение условий выпуклости и монотонного возрастания кривой °s = f (sS). Эти условия обеспечиваются при f '(sS) >0 и f "(ss) <0 и для предлагаемой функции (4) выполняются в случае:

Г ° m 1 ” 1⁽ ” 1 - 1) —

I ° 0,2

Л ” 1 ^{- 2}

- п7

+ m ₂ n ₂ ( n ₂

- 1)

( °

L ° 0,2

-

Г ° m l ” 1⁽ ” 1 ^- 1) —

I ° 0,2

Л ” 1 - ²

- п7

+ m ₂ n ₂( n ₂ - 1)

L

° 0,2

Л ” 2

^{- П} 2

Л ” 2 - ²

П 2      >  ⁰ ,

- 2

+ m ₃ n ₃( n ₃

° 0,2 <  ° s <  ° 0,5 ;

- 1)

° .

к ° 0,2

^{- П} 3

- 2

> 0,

° 0,5 <  ° s <  ° u .

Конструкция сплайна в функции приближения (4) дана в общем виде, т.е. с переменными значениями всех коэффициентов, включая показатели степени n i . Подбор этих коэффициентов осуществляется исходя из условий (5), что несколько усложняет расчет, но вместе с тем позволяет аппроксимировать диаграмму с любой необходимой для конкретной задачи точностью, вплоть до совпадения опытной и расчетной диаграмм.

Численный анализ системы (4) также показал, что сплайн-функция общего вида легко формализуется в различных вариантах, упрощенных и более удобных для конкретного практического применения, сохраняя при этом высокую точность приближения. Так, в данной работе в порядке численного эксперимента производилась аппроксимация опытной диаграммы исследуемой стали класса Ат-1200 (Ат-VII) сплайнами невысоких степеней с постоянными значениями коэффициентов степени n i , а именно сплайном первого порядка, посредством квадратичной сплайн-интерполяции и кубическим сплайном. Анализ результатов показывает, что приближение нелинейной части диаграммы наиболее естественным образом обеспечивается при использовании кубического сплайна.

Расчетная диаграмма стали класса Ат-1200 (Ат-VII), приведенная на рисунке 1, получена как раз с использованием системы (4) при n 1 =n₂=n₃=3 , т.е. посредством кубического сплайна. Это значительно упрощает алгоритм решения, хотя и вызывает некоторую погрешность (в данном случае не более 1,5%), не превышающую допустимых в практике инженерных расчетов значений.

При задании функции f (°s) в виде кубического сплайна выражение (1) приобретает вид:

r

Е ^{( 8} s,pl i + ⁸ S,pl + ⁸ sc +

) = m l

ст

l ст 0u2

- n7

+ m ₂

ст l ст p

v3 v- П 2) + m 31 ст p - П 3 ,

где ст 0™2p - исходное (до преднапряжения) значение условного предела текучести.

Результаты определения основных параметров «упрочненной» (см. рис. 2) диаграммы класса Ат-1200 (Ат-VII) по выражению (6) приводятся в таблице 3 и свидетельствуют о высокой сходимости опытных и расчетных данных.

Таблица 3

Сравнение опытных и расчетных по формуле (6) параметров упрочненной при предварительном напряжении диаграммы растяжения стали класса Ат-1200 (Ат-VII)

Предварительное напряжение ст sp , Мпа	ст р sup ст 0,2	Параметры «упрочненной» диаграммы (расчетные значения), Мпа			Величина расхождения расчетных и опытных значений, %
		calc ст 0,05	calc ст 0,2	calc ст 0,5	exp        calc ст 0,05 - ст 0,05	exp        calc ст 0,2 - ст 0,2	exp        calc ст 0,5 - ст 0,5
					calc ст 0,05	calc ст 0,2	calc ст 0,5
564	~0,55	862	1053	1162	4,52	0,19	- 0,26
569		941	1100	1207	- 1,28	- 1,36	- 1,08
601		902	1114	1241	3,88	0,81	0,56
818	~0,75	978	1126	1255	- 0,31	- 0,27	- 1,83
816		955	1111	1211	3,25	- 0,18	0,00
1078	~0,95	1156	1216	1268	1,56	0,99	0,55
1048		1123	1209	1294	3,82	1,16	0,31
1053		1140	1221	1290	0,70	0,41	1,24

Как видно из таблицы 3, средние величины относительного превышения опытных значений над расчетными составляют: А ст _{0 05} = 2,02%; Аст _{0 2} = 0,22%; А ст ₀ 5 = - 0,06%.

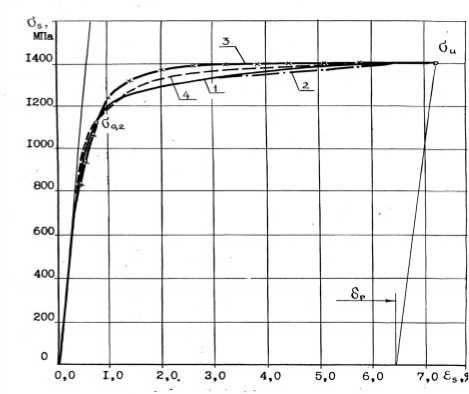
Рис. 3. К аналитическому описанию диаграммы растяжения высокопрочной арматурной стали класса Ат-1200 (Ат-VII) на примере диаметра 25 мм: 1 - опытная кривая; 2 - расчетная по формуле (4) при n 1 =n₂=n 3 =3 ; 3 - расчетная по работе [6]; 4 - расчетная по работе [7]

Таким образом, экспериментально выявленный эффект деформационнотемпературного упрочнения стали класса Ат-1200 (Ат-VII) достоверно оценивается с использованием расчетного аппарата, основу которого составляет выражение (1), при аппроксимации исходной и «упрочненной» диаграмм деформирования посредством многоинтервальной (сплайн) интерполяции.

Предложенный метод носит универсальный характер и может быть использован при прочностных расчетах предварительно напряженных конструкции с другими видами арматурной стали.