Расчетно-экспериментальное исследование воздействия солнечной радиации на направляющую трубу с термозащитным кожухом

В длинных направляющих трубах температурные градиенты из-за несимметричного нагрева или охлаждения по периметру трубы могут привести к возникновению температурных деформаций. Такие деформации являются причиной искривления оси канала трубы относительно теоретической, что значительно снижает эксплуатационные характеристики изделия в целом. Причиной неравномерного распределения температур по трубе может быть одностороннее воздействие солнечной радиации, ветра, дождя или снега в совокупности с высокотемпературным нагревом внутренней поверхности трубы горячими топливными газами при ее функционировании [1-6].

Для решения данной проблемы еще с середины 60-х годов, как в СССР, так и за рубежом, стали использовать специальные термозащитные кожуха (ТЗК) – оболочки, защищающие трубу от неблагоприятных температурных воздействий.

Следует отметить, что если на зарубежных изделиях в настоящее время используются

ТЗК, выполненные из неметаллических композиционных материалов, то отечественные конструкции ориентированы на использовании тонкостенных металлических кожухов, выполненных из алюминия. Это является усложняющим фактором по быстросъемности при их замене и утяжеляет трубную конструкцию в сборе.

В АО «ЦНИИМ» была отработана технология изготовления ТЗК из композиционного материала, а также разработана опытная конструкция ТЗК (рис.1). Опытная конструкция приближена к конструкции штатного ТЗК, и имеет одинаковые элементы крепления на защищаемую трубу.

Композиционный ТЗК представляет собой оболочку вращения, толщиной около 1,5 мм, с торцевыми изгибами, повторяющими контур трубы. Оболочка выполнена из композиционно-волокнистого материала (КВМ) с внутренней поверхностью из алюминиевой фольги.

Рисунок 1 – Секция ТЗК из композиционного материала

Практика показывает, что данная опытная конструкция из КВМ обеспечивает сокращение времени монтажа и демонтажа на трубе изделия по сравнению со штатным ТЗК в 13 раз.

Также была проведена расчетноэкспериментальная оценка эффективности ТЗК при воздействии солнечной радиации на трубу с кожухом. Для определения температурного поля была построена модель направляющей трубы с кожухом в виде двух цилиндрических оболочек, разделенных воздушной прослойкой. В данной модели наружная поверхность термозащитного кожуха подвергается одностороннему воздействию радиационного потока от солнца q = 1100 ^ 1150 ^Вт/_М 2 •

Для уточнения и конкретизации параметров тепловой модели и проведения расчетов была сконструирована и смонтирована экспериментальная установка для имитации воздействия солнечной радиации на направляющую трубу изделия в лабораторных условиях (рис. 2). Основным назначением данной установки является получение данных для параметрической идентификации расчетной модели, и таким образом, повышение достоверности рас- четных результатов. Схема установки представлена на рис.2.

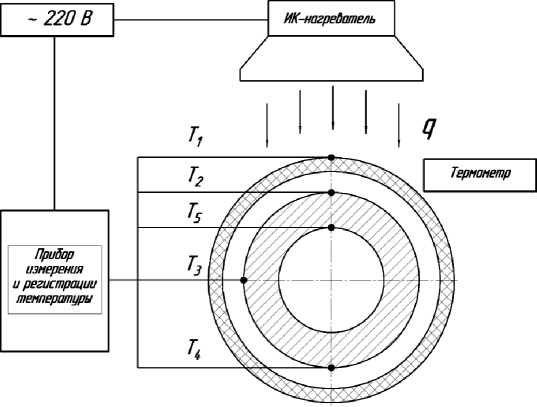
Рисунок 2 – Схема экспериментальной установки

Для исследования эффективности ТЗК из КВМ, при имитации воздействия солнечной радиации на трубу, были изготовлены три экспериментальных кожуха: ТЗК из алюминиевого листа, из стеклопластика и углепластика с внутренней поверхностью из фольги. Все ТЗК были окрашены в защитную краску.

Замеры температуры производились в одном сечении в 5 точках. Регистрация температуры в течение всего времени нагрева производилась постоянно в точках 2 и 4 (верхняя и нижняя поверхность трубы). Также регистрировалась температура окружающей среды. Результаты измерений для всех ТЗК обобщены в табл. 1. Определяющим критерием оценки эффективности ТЗК принято значение градиента температур между верхней и нижней поверхностью трубы Д Т .

Таблица 1 – Результаты измерений

Образец ТЗК	Толщина кожуха S, мм	Величина зазора H, мм	Т в ,ос	Т 1 ,с	Т 2 ,с	Т 3 ,с	Т 4 ,с	Т 5 ,с	Д Т ,°с
Алюминиевый	0,5	5	35	84	46,3	45,2	43,5	46	2,8
Стеклопластик с фольгой	1,5	10	35	108	42,6	40,3	38,7	41,8	3,9
Углепластик с фольгой	1,5	10	35	102	41,9	41	40,6	41,7	1,36
Углепластик без фольги	1,5	10	35	99	50,4	47,2	45,4	49,6	4,7

Таким образом, имея представления об  так и на поверхности трубы, можно уточнить уровне температур, как на поверхности кожуха,  достоверность математической модели, реали- зация которой позволяет установить оптимальные размеры воздушного зазора между трубой и кожухом, а также толщину самого термоза- щитного кожуха.

Задача рассматривается в стационарной постановке, при которой происходит максимальный изгиб трубы от действия несимметричного теплового потока. В этом случае уравнение теплопроводности в общем виде для ка- ждого из элементов конструкции имеет вид:

д дТ д дТ д дТ

— (К— )+— ( К — ) +—(К —) + q_v = 0. x    y    zV

∂x    ∂x ∂y    ∂y ∂z    ∂z где λ , λ , λz – теплопроводности материала в направлении осей х, у, z, Т – температура, q – объемные стоки тепла (в данном случае q =0).

Для формулировки граничных условий к этим уравнениям был рассмотрен тепловой баланс на поверхностях элементов конструкции. Тепловое взаимодействие между трубой, кожухом и окружающей средой схематично представлено на рис. 3.

Qa = <7r + а_к • (Т_А - Г,) + Е_Л<Г_О(Т/ - Т*)

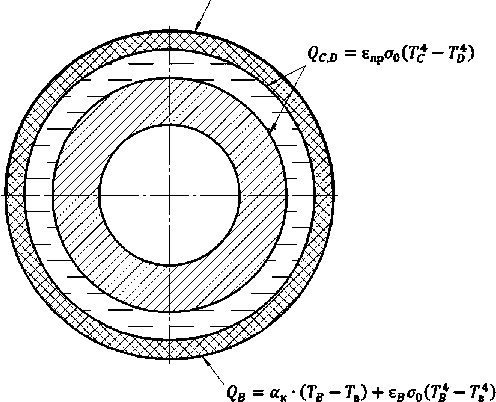
Рисунок 3 – Расчетная модель с граничными условиями

Верхняя граница А подвергается воздействию солнечного радиационного потока . Также она учавствует в конвективном и лучистом теплообмене с окружающим воздухом. Граничное условие запишем:

Q A = ^qr ^{+ a} k ' ^(TA ^{- Т}в ) ^{+ е} А ' ⁷ 0 ' ^{( T}A ^- T ⁴ ) , где _к – конвективный коэффициент теплоотдачи с наружной поверхности кожуха, ԑ – степень черноты наружной поверхности кожуха,

– температура поверхности A , _в – темпе-

Граничное условие для поверхности B запишется:

Q B = ^a k ' ^{( T}B ^{- Т}в ) ^{+ е} В ' <7 0 ' ^(TBi ^- T B^ .

Внутренняя поверхность кожуха C участвует в теплообмене с поверхностью трубы. Так как величина воздушного зазора между кожухом и трубой мала, необходимо установить возможность протекания конвективного теплообмена между ними.

Для описания сложного процесса теплообмена в ограниченном замкнутом пространстве используют критериальное уравнение [8]:

E k = f ( Gr • Pr), где _к – коэффициент конвекции, – число Грасгофа, – число Прандтля.

Если    ∙   > 1000, то происходит конвективный теплообмен, если     ∙    ≤

1000, то конвективного теплообмена нет ( к =1).

Исходя из экспериментальных данных, по критерию ∙   >< 1000, было определе но что, при воздушных зазорах до 10 мм конвективный теплообмен отсутствует.

Таким образом теплообмен между внутренней поверхностью кожуха С и поверхностью трубы D , будет происходить за счет лучистой составляющей:

QC,D = £пр • 70 • (TC - TD^ , где εпр – приведенная степень черноты (вычисляется через степени черноты взаимодействующих поверхностей).

Основные трудности анализа конвективного теплообмена связаны с установлением вида зависимости коэффициента теплоотдачи от определяющих его параметров. В большинстве случаев вид этих зависимостей устанавливается при обобщении экспериментальных данных [7].

При расчете теплопередачи цилиндрической поверхности в условиях естественной конвекции в неограниченное пространство используется неравенство (1):

( t - t c ) <  (8|°)³[ ° C ] .                 (1)

Если определяющий размер (L, мм) плоской или цилиндрической поверхности и ее температурный напор ( -  ) удовлетворяют неравенству (1), то конвективный коэффициент теплоотдачи будем рассчитывать по формуле:

a, = 1,35 ^ ( t - t ^ ) 14 [ -7Вт_ ].        (2)

k

D    м ⋅ °С ратура окружающего воздуха.

Исходные данные для теплового расчета приведены в таблице 2. Температура окружающего воздуха для всех расчетных случаев составляла 35 Т.

Расчет температурного поля данной конструкции производится методом конечных элементов в программном комплексе Ansys.

Таблица 2 – Исходные данные для теплового расчета

Образец ТЗК	Толщина кожуха S, мм	Величина зазора Н, мм	Вт , м Т	Вт “ к '     м 2-Т	еа,в	Ес	ed
Алюминиевый	0,5	5	160	4,5	0,8	0,4	0,8
Стеклопластиковый	1,5	10	0,5	5,6	0,8	0,04	0,8
Углепластиковый	1,5	10	1,6	5,7	0,8	0,04	0,8

В результате расчета было получено температурное поле трубы с различными ТЗК. Значения температур в контрольных точках представлены в таблице 3. Как видно из таблицы наименьший градиент температур достигается с образцом ТЗК из углепластика.

Таблица 3 – Результаты теплового расчета

Образец ТЗК	Толщина кожуха S, мм	Величина зазора Н, мм	Т в ,Т	Т i ,T	Т,Т	Т з ,Т	Т 4 ,Т	т 5,т	Д Т ,т
Алюминиевый	0,5	5	35	80,32	47,25	47,75	46,37	47,2	0,9
Стеклопластик с фольгой	1,5	10	35	102	44,3	43,8	43,54	44,2	0,76
Углепластик с фольгой	1,5	10	35	101,7	42,1	41,6	41,34	42	0,66

На рис. 4 представлено температурное поле трубы с ТЗК из углепластика с внутренним слоем фольги. По результатам расчета, было установлено, что применение такого кожуха снижает градиент температур до 0, 66 Т.

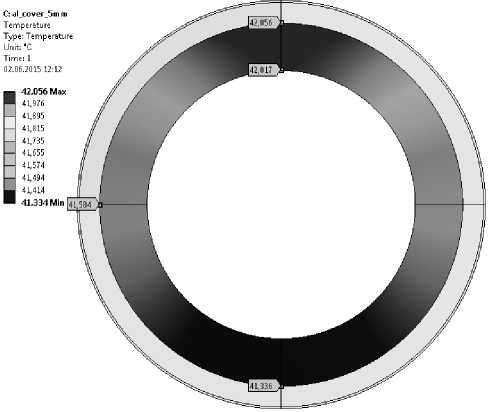
Рисунок 4 – Температурное поле трубы с ТЗК из углепластика

По данным расчета можно сделать выводы о том, что градиент температур будет уменьшаться с увеличением толщины кожуха и увеличением воздушного зазора (рис. 5). Поскольку имеются ограничения к конструкции кожуха (радиус обметания изделия, масса кожуха), то оптимальная толщина принята 1,5 мм, а величина воздушного зазора – 10 мм.

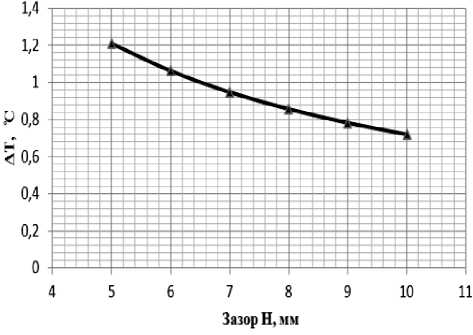
Рисунок 5 – Зависимость градиента температур от величины зазора (для углепластикового кожуха)

Для оценки значения деформаций, возникающих от температурного воздействия солнечной радиации, был произведен расчет напряженно-деформированного состояния, сопряженный с тепловым расчетом. В результате расчета получены величины максимальных перемещений, возникающих в результате несимметричного воздействия солнечной радиации.

По результатам расчета было выявлено, что минимальные искривление оси трубы достигаются при использовании ТЗК из углепластика (рис.6).

• б)    повышение теплопроводности связующего, за счет введения мелкодисперсных наполнителей;

• в)    увеличение толщины кожуха (при допустимом увеличении массы и габаритов).

При дальнейшей проработке и корректировке разработанной методики оценки эффективности ТЗК необходимо учесть: нагрев внутренней поверхности канала трубы при ее функционировании, зависимость коэффициента теплоотдачи от температуры и координаты, а также анизотропию свойств материала.

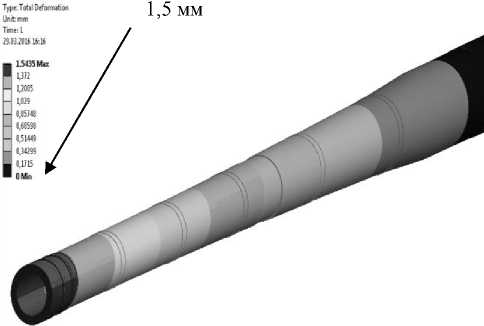
Рисунок 6 – Поперечные перемещения трубы под действием температурных напряжений (с углепластиковым кожухом)

Выводы

Разработанная расчетная модель, реализованная в программном комплексе Ansys, позволяет найти оптимальные конструктивные параметры ТЗК и теплофизические характеристики. Экспериментальные данные показали адекватность применяемого расчетного метода и позволили скорректировать модель для исследования воздействия солнечной радиации на тепловое состояние трубы.

По результатам проведенных исследований можно определить пути повышения эффективности разрабатываемого ТЗК из композиционного материала:

• а) применение высокотеплопроводных волокон;