Расчетно-экспериментальный анализ собственных и критических частот и форм высокооборотного ротора микрогазотурбинной установки

Микрогазотурбинные установки малой мощности используют на промышленных предприятиях, в медицинских учреждениях, жилищных коттеджных поселках; на магистральных газопроводах, нефтепроводах, газораспределительных станциях; в энергодефицитных районах Крайнего Севера, Сибири, Дальнего Востока; для резервирования линий электропередач, питающих ответственных потребителей энергии, для восполнения дефицита электроэнергии, вызванного стихийными бедствиями и другими чрезвычайными ситуациями; в качестве мобильных источников электрической и тепловой энергии для нужд МЧС.

Наиболее ответственной частью МГТУ является ротор, рабочая частота которого составляет 65 000 мин–1. Он состоит из ротора турбокомпрессора (ТК) и ротора стартер-генератора (СГ), соединенных упругой связью (рис. 1).

Одним из требований, предъявляемых к высокооборотному ротору, является исключение попадания его критических частот в диапазон ± 30 % от рабочей частоты вращения (45 500–84 500 мин–1) [5]. Таким образом, возникает задача разработки ротора, обладающего критическими частотами, которые не попадают в запретную область. Аналогичной проблеме посвящены работы [1, 2, 6, 7, 17–21].

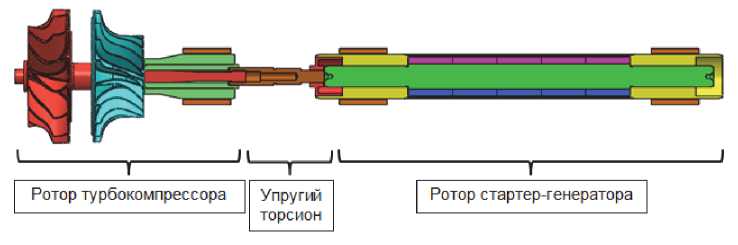
Рис. 1. Ротор МГТУ

Оценка собственных частот и форм ротора МГТУ . Оценка выполнена методом конечных элементов (КЭ) в пакете Ansys Workbench. Предполагалось, что все элементы ротора абсолютно жестко связаны друг с другом. Ротор считали незакрепленным. Собственные частоты изгибных колебаний ротора в диапазоне от 0 до 120 000 мин^–1 (2000 Гц) приведены в табл. 1, частоты и формы крутильных и продольных колебаний не рассматриваются.

Первые шесть собственных частот соответствуют колебаниям ротора как абсолютно твердого тела. Седьмой и восьмой частотам соответствуют колебания ротора турбокомпрессора и ротора стартер-генератора как абсолютно твердых тел, связанных упругим торсионом с малой изгиб-ной жесткостью (первая изгибная форма всего ротора). Второй изгибной форме ротора соответствуют 11 и 12 собственные частоты (колебания в двух взаимно перпендикулярных плоскостях). Третья изгибная собственная форма ротора соответствует частотам 1165 и 1453 Гц. Эта форма определяется, в первую очередь, параметрами ротора стартер-генератора. Четвертая изгибная форма ротора соответствует частотам 1302 и 1378 Гц. На этой форме преимущественно колеблется ротор турбокомпрессора.

Как видно из табл. 1, частоты, соответствующие третьей и четвертой изгибной форме, оказались в недопустимой области 45 500–84 500 мин–1.

Таблица 1

Результаты расчета собственных частот и форм ротора МГТУ при его поперечных колебаниях

№ собственной формы

Форма колебаний на собственной частоте

Собственная частота

1–4

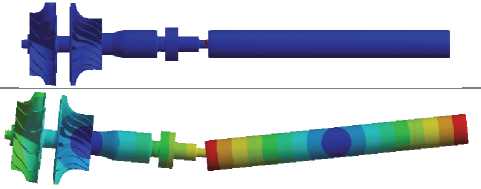
Первая изгибная собственная форма

0 Гц (0 мин–1)

Вторая изгибная собственная форма

Третья изгибная собственная форма

78 Гц (4692 мин–1)

87 Гц (5196 мин–1)

489 Гц (29 322 мин–1)

499 Гц (29 910 мин–1)

1165 Гц (69 900 мин–1)

1453 Гц (87 180 мин–1)

Четвертая изгибная собственная форма

1302 Гц (78 120 мин–1)

1378 Гц (82 680 мин–1)

Определение собственных частот подсистем ротора МГТУ. С целью анализа собственных частот и форм, оказавшихся в недопустимом диапазоне, принято решение оценить собственные частоты роторов ТК и СГ по отдельности. Ротор ТК приведен на рис. 2. Конструкция ротора СГ изображена на рис. 3.

Оценка собственных частот роторов ТК и СГ выполнена методом КЭ. Собственные частоты и соответствующие им формы приведены в табл. 2 и 3.

Первой изгибной частоте (табл. 2) соответствуют колебания элемента ротора ТК. Эта форма не является опасной. Наибольший интерес представляет вторая форма изгибных колебаний. Однако соответствующая ей частота – 2228 Гц (133 680 мин–1) расположена далеко за пределами диапазона 45 500–84 500 мин–1. Таким образом, ротор ТК обладает достаточно высокой изгибной жесткостью.

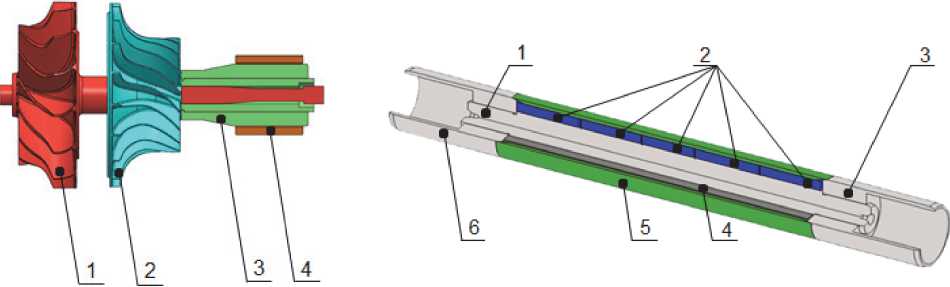
Рис. 2. Ротор ТК: 1 – колесо центростреми- Рис. 3. Основные элементы ротора СГ: 1 – вал; 2 – магниты; тельной турбины, созданное заодно с ва-         3,6 – втулки; 4 – вставки (2 шт.); 5 – углелента лом; 2 – колесо центробежного компрессора; 3 – втулка; 4 – радиальный лепестковый газодинамический подшипник

Таблица 2

Результаты расчета собственных частот и изгибных форм ротора ТК

Собственная форма

Собственная частота

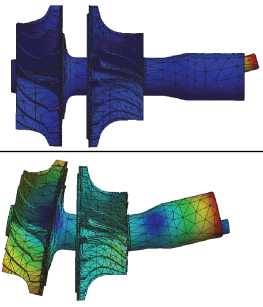
870 Гц (52 200 мин–1)

873 Гц (52 380 мин–1)

2228 Гц (133 680 мин–1)

2229 Гц (133 740 мин–1)

Таблица 3

Собственные частоты и формы ротора СГ при «жестком» контакте элементов ротора

Собственная форма

Собственная частота

1023 Гц (61 380 мин–1)

1024 Гц (61 440 мин–1)

2437 Гц (146 220 мин–1)

2438 Гц (146 280 мин–1)

Первая собственная частота изгибных колебаний ротора СГ, найденная расчетным путем (табл. 3), составила 1023 Гц (61 380 мин–1) и оказалась недопустимо близкой к рабочей частоте вращения 65 000 мин–1.

Экспериментальная оценка собственных частот и форм ротора СГ. В эксперименте ротор вывешивали на податливых тросах (рис. 4). Как показали предварительные эксперименты, частота колебаний ротора как твердого тела на упругой подвеске составила ок о ло 9,4 Гц (при низшей частоте изгибных колебаний 672 Гц). Такая подвеска является податливо й и практически не оказывает влияния на собственные частоты и формы ротора при его изгибных колебаниях. С целью определения частот и форм изгибных колебаний на внешней поверхности ротора наклеены десять однокомпонентных акселерометров (см. рис. 4). Возбуждение колеба н ий осуществлялось при помощи ударного молотка. Испытания проведены в модуле Impact Testing пакета LMS Test.Lab 13A с использованием технологии экспериментального модального анализа [3]. Результаты эксперимента приведены в табл. 4. Установлено, что результаты расчета о т личаются от эксперимента на 30 %.

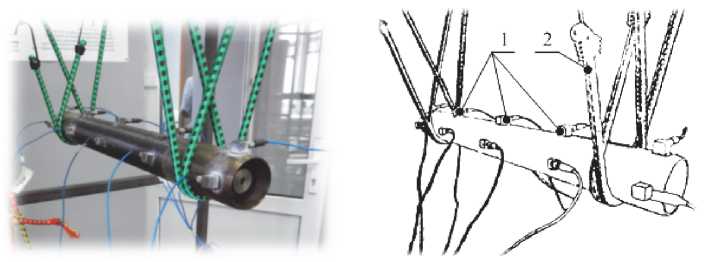
Рис. 4. Экспериментальная установка: 1 – однокомпонентные акселерометры (10 шт.); 2 – податливые тросы (4 шт.)

Таблица 4

Собственные частоты и формы изгибных колебаний ротора СГ, найденные экспериментальным путем

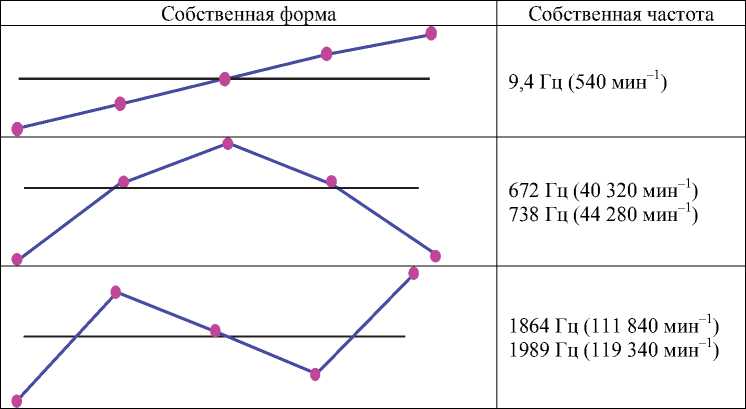
Одной из возможных причин такого различия являются условия сопряжения магнитов и стального вала в конечно-элементной модели. Для подтверждения этой ги п отезы выполнен расчет методом КЭ при следующем условии: магниты абсолютно жестко прилегают тол ь ко к угле-ленте, не соединены друг с другом и с валом. Резуль т аты расчета представлены в табл. 5.

Анализ результатов (табл. 3, табл. 5) показывает, что в изготовленной конструкции реальные условия сопряжения магнитов и вала находятся между двумя предельными случаями – когда магниты соединены с валом по всей цилиндрической поверхности, и когда магниты не связаны с валом, но жестко прилегают к углеленте. Таким образом, собственная частота изготовленного ротора стартер-генератора, полученная экспериментальным путем, является достоверной и составляет 672 Гц (40 320 мин–1) в вертикальной и 738 Гц (44 280 мин–1) в горизонтальной плоскости. Результаты определения собственных частот и форм ротора стартер-генератора приведены в табл. 6.

Таблица 5

Собственные частоты и формы корректированной модели ротора СГ при «мягком» контакте элементов ротора

Форма колебаний на собственной частоте	Собственная частота
	612 Гц (36 720 мин–1)
	631 Гц (37 860 мин–1)

Таблица 6

Первая собственная частота изгибных колебаний ротора стартер-генератора

Численное определение («жесткий» контакт элементов ротора)	Экспериментальный модальный ана л из	Уточненный расчет («мягкий» контакт элементов ротора)
1023 Гц	672 Гц	612 Гц
1024 Гц	738 Гц	631 Гц

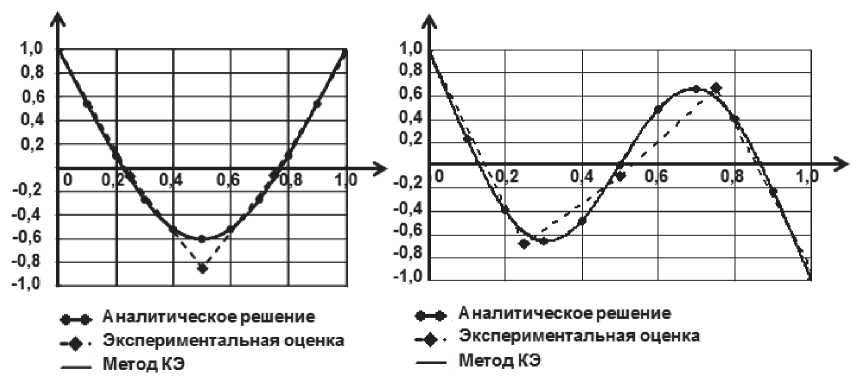
По результатам анализа (см. табл. 6) принято решение о создании эквивалентной м о дели ротора стартер-генератора, собственные частоты и формы которой близки к результатам эксперимента. Такая модель построена по критериям равенства масс, длин и первых собственн ы х частот изгибных колебаний эквивалентной модели и ее реального прототипа (см. рис. 4) [13]. Результаты расчета собственных частот эквивалентной модели ротора СГ приведены н а рис. 5 и в табл. 7.

а)

б)

Рис. 5. Сравнение собственных форм ротора СГ, полученных аналитически, экспериментально и методом КЭ: а – первая изгибная собственная форма; б – вторая изгибная собственная форма

Таблица 7

Сравнение собственных частот эквивалентной модели ротора СГ, Гц

Эквивалентный ротор СГ, аналитическое решение [4]	Эксперимент (рис. 4)	Эквивалентный ротор СГ. Метод К Э
738	738	737
2040	1989	2032

Таким образом, построена эквивалентная модель ротора СГ, у которой близкими к эксперименту оказались не только первая, но и вторая собственные частоты и формы изгибных колебаний.

Оценка влияния жесткостей подшипниковых опор на критические частоты ротора. В пакете Ansys Mechanical APDL создана упрощенная балочная КЭ модель ротора (рис. 6) и выполнен расчет критических частот ротора [4] в широком диапазоне жесткостей опор [14].

Как показал расчет (рис. 7), при жесткостях опор, меньших, чем 106 Н/м, упругие опоры практически не оказывают влияния на критические частоты и формы ротора, т. е. его можно считать незакрепленным. Таким образом, для того, чтобы удовлетворить требованиям по критическим частотам, необходимо использовать подшипниковые опоры, жесткость которых не превышает 106 Н/м.

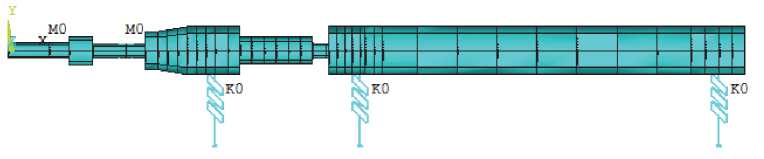
Рис. 6. Балочная модель ротора МГТУ

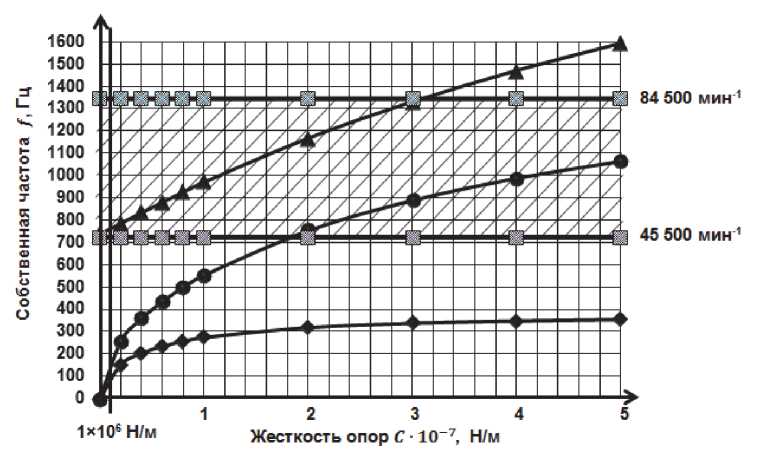
Рис. 7. Зависимость критических частот ротора от жесткостей опор

Расчет собственных частот ротора МГТУ с эквивалентным ротором СГ. Выполнен расчет собственных частот ротора МГТУ в условиях свободного вывешивания (что соответствует подшипниковым опорам с жесткостями меньшими, чем 10⁶ Н/м), с учетом эквивалентной модели ротора СГ. Расчет показал, что собственные частоты такой модели не соответствуют предъявляемому к конструкции требованию. Сделан вывод о том, что причиной этому является жесткость торсиона.

Конструкторской группой университета предложен ряд моделей с различными упругими связями (рис. 8). Наиболее удачной из них оказалась конструкция ротора МГТУ, в которой ротор ТК и СГ соединены торсионом с двумя мембранами (рис. 9). Собственные частоты и формы модели ротора МГТУ с выбранным вариантом упругой связи и эквивалентной моделью ротора СГ представлены в табл. 8.

а)                                                                      б)

в)

Рис. 8. Модели с различными вариантами упругой связи

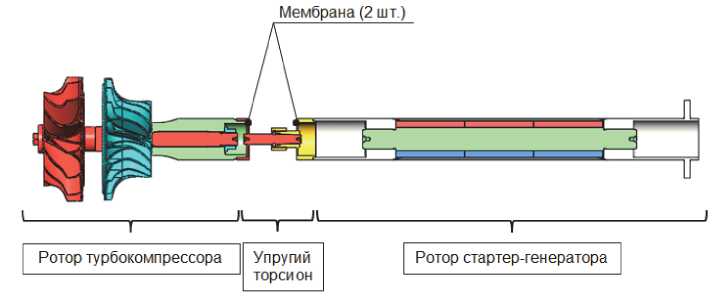
Рис. 9. Модель ротора МГТУ с выбранным вариантом упругой связи

Собственные частоты и формы ротора МГТУ

Таблица 8

Форма колебаний на собственной частоте	Собственная частота
Первая изгибная форма ротора МГТУ	51 Гц (3079,44 мин–1) 52 Гц (3129,48 мин–1)
Вторая изгибная форма ротора МГТУ	308 Гц (18 453 мин–1) 309 Гц (18 532 мин–1)
Третья изгибная форма ротора МГТУ	730 Гц (43 783 мин–1) 731 Гц (43 818 мин–1)
Четвертая изгибная форма ротора МГТУ	1497 Гц (89 808 мин–1) 1498 Гц (89 862 мин–1)
^I^^^^jjl^^^^u^8^^^^^^y^^^^^^^j^§^^^^^^^^ Пятая изгибная форма ротора МГТУ	1766,6 Гц (105 996 мин–1) 1766,9 Гц (106 014 мин–1)

Определение критических частот трехмерной модели ротора МГТУ.

Задача решалась с использованием КЭ пакета Ansys Workbench. В результате решения задачи об определении критических частот ротора МГТУ построена диаграмма Кэмпбелла [8–12] (рис. 10). Значения критических частот ротора МГТУ приведены в табл. 9. Из сопоставления результатов, приведенных в табл. 8 и 9, следует, что первая, вторая и третья критические частоты ротора, найденные с учетом гироскопических моментов (табл. 9), оказались на 7, 5 и 4 % выше, чем соответствующие собственные частоты (табл. 8).

Как следует из расчетов, критические частоты ротора (табл. 9) оказываются вне диапазона ± 30 % от рабочей частоты вращения (45 500–84 500 мин–1), что удовлетворяет предъявляемым к конструкции требованиям.

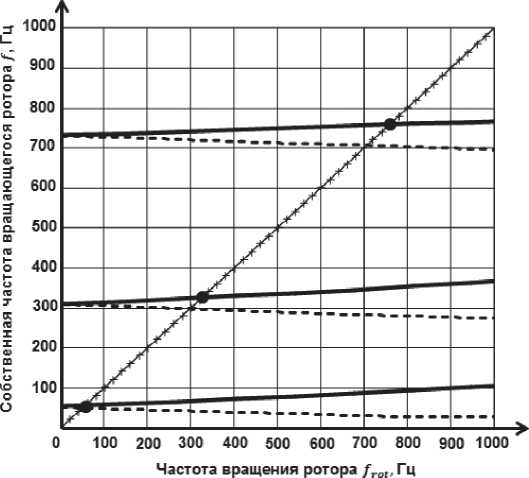
— Прямая

---Обратная прецессия

+++ Луч 45’

Рис. 10. Диаграмма Кэмпбелла

Таблица 9

Критические частоты ротора МГТУ

№ изгибной формы	Прямая прецессия	Обратная прецессия
1	54,4 Гц (3263,46 мин–1)	49,5 Гц (2969,94 мин–1)
2	324,2 Гц (19450,02 мин–1)	295,8 Гц (17746,44 мин–1)
3	757,5 Гц (45451,8 мин–1)	705,4 Гц (42325,32 мин–1)

Таким образом, на основе расчетно-экспериментального подхода разработаны рекомендации для конструкции ротора МГТУ: жесткости подшипниковых опор не должны превышать 106 Н/м; ротор турбокомпрессора и ротор стартер-генератора должны быть связаны упругим элементом с малой изгибной жесткостью; конструктивное исполнение упругой связи, при которой критические частоты ротора оказываются вне диапазона ± 30 % от рабочей частоты вращения (45 500–84 500 мин–1).

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках комплексного проекта «Создание производства модельного ряда микротурбинных энергоустановок нового поколения» по договору № 02.G25.31.0078 от 23.05.2013 г. между Министерством образования и науки Российской Федерации и Открытым акционерным обществом «Специальное конструкторское бюро «Турбина» в кооперации с головным исполнителем НИОКТР – Федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Южно-Уральский государственный университет» (национальный исследовательский университет).