Расчетно-экспериментальный метод определения акустических сопротивлений упругих элементов трубопроводов

Электронный журнал «Техническая акустика»

В инженерной практике проектирования средств снижения передачи колебаний по жидкостному тракту трубопроводов гидравлических и воздушных систем упругие элементы (гибкие вставки) принято характеризовать параметрами, называемыми акустическими сопротивлениями. По определению это отношения звуковых давлений на входе и выходе элемента к колебательной скорости на входе при нулевой скорости на выходе. Эти параметры достаточны для описания передаточных свойств собственно упругого элемента и являются необходимыми для акустических расчетов систем с учетом происходящих в них волновых процессов. Пока далеко не всегда возможно найти эти параметры расчетом. В большинстве случаев их определяют экспериментально.

Когда предметом исследований являются элементы с капельной жидкостью,

обеспечить жесткие требования по граничным условиям не всегда удается. Тогда появляются области частот, где вещественные части акустических сопротивлений отрицательны по знаку, вопреки их физической сути. В таких случаях требуется логическая операция по сглаживанию данных измерений.

Ниже рассматривается расчетно-экспериментальный метод, который позволяет упростить процедуру определения акустических сопротивлений и может быть использован при анализе результатов эксперимента. Исследуемый упругий элемент представляется в виде каскадного соединения четырехполюсников, эквивалентных его упругой и жестким частям. Параметры (скорость звука и коэффициент потерь) упругой части элемента предложено определять по экстремуму модуля отношения звукового давления к колебательной скорости во входной измерительной камере, а параметры остальных частей — расчетом.

In engineering practice the means of noise control for liquid path of hydraulic and air pipelines (flexible insertions, hoses, bellows and etc.) are characterized by acoustic impedance. By definition it is the relation of sound pressure at the input and output of the element to the velocity at the input when velocity at the output is equal to 0. These parameters are sufficient for the description of transfer properties of an actual elastic element and are necessary for calculation. It is impossible as a rule to calculate these parameters. For the most part they are determined experimentally.

Calculated and experimental method, which allows to simplify procedure of acoustic impedance determination and to use experimental results in analysis, is considered. The elastic element is represented as a cascade connection of quadripoles, which are equivalent to elastic and rigid parts of elastic element. The elastic part parameters (sound speed and loss factor) are determined from extremum of the absolute value of relation of sound pressure to velocity at the measuring chamber input. The other parameters are calculated.

При экспериментальном определении акустических сопротивлений упругих элементов трубопроводов гидравлических систем трудно полностью избавиться от погрешностей, связанных, в основном, с перетеканием энергии из структурного в жидкостной тракт. Имеются области частот, где реальная составляющая входного Z 11 сопротивления (и передаточного сопротивления Z 21 в области до первого минимума Z 11 ), вопреки физической сути этих сопротивлений, отрицательны по знаку. Жесткое крепление испытываемого упругого элемента по краям и в промежутке между ними с целью уменьшения обмена энергии между обоими трактами часто не дает желаемого результата. В таких случаях требуется логическая операция по сглаживанию данных измерений, например, интерполяция.

Ниже рассматривается расчетно-экспериментальный метод, значительно упрощающий процедуру определения акустических сопротивлений Z 11 и Z 21 и не требующий проведения дополнительных операций сглаживания.

Рассмотрим установку, состоящую из исследуемого упругого элемента (УЭ), который с одного конца закрыт жесткой крышкой, а к другому его концу присоединен отрезок трубы (рис. 1 ). Как обычно, будем учитывать только плоские волны внутри установки, пренебрегая неоднородными волнами в местах изменения скорости звука.

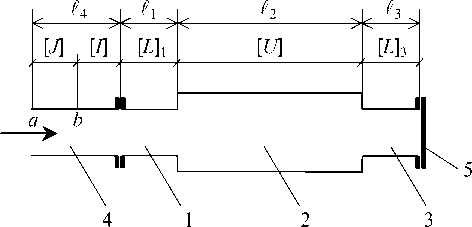
Рис. 1. Схема установки с УЭ

1, 3 – жесткие арматурные части УЭ; 2 – упругая часть УЭ; 4 – отрезок трубы; 5 – крышка

Допустим, что нам известно из эксперимента (например с помощью методов [ 1—4] ) комплексное отношение Z b a звукового давления P b в точке b к объемной колебательной скорости V a в точке a . Так как один конец установки закрыт жесткой крышкой и здесь колебательная скорость равна нулю, то

Z ba = P b V = M 1, / T 21 ,                                                         (1)

где M 11 = P _b/ P 2 — параметр передачи участка установки от точки b до точки 2 (до крышки); T 21 = V _a/ P 2 — параметр передачи участка установки от точки а до точки 2 (до крышки).

В соответствии с принятыми на рис. 1 обозначениями матриц передачи отдельных участков имеем

[A ] =

[M ] =

[T ] =

^A 11

A ₂₁

M 11

^M 21

T

T ₁₁

T

^T 21

^A 12

A ₂₂

= [L L*.]x[L ] 3

M 12

^M 22

T ¹²

T

¹ 22 J

= [ I ] x [ A ] ,

= [ J ] x [ M ] ,

Интерес представляют условия, при которых модули величин M 11 и T 21 минимальны.

Затуханием звука в пределах жестких участков установки можно пренебречь вследствие

относительной малости их длин и потерь в них. Поэтому их матрицы передачи

[J ] , [I ] , [L ]

легко можно найти расчетом, по скорости звука.

Затуханием звука в пределах упругой части УЭ (с матрицей передачи

[ U ] )

пренебречь

нельзя и поэтому коэффициент распространения ( Г 2 ) и волновое сопротивление ( Z 02 ) этой

части установки являются величинами комплексными:

^Г 2 = ^{( в} 2 + ^{j a} 02 ) ^£ 2 ,

7 =

Z 02

Рг [1'Р 1

° 2 у ^а 02 J

где р — плотность жидкости, c ₀₂ — скорость звука (вещественная часть) в упругой части УЭ, S 2 - площадь проходного сечения упругого элемента, в ₂ и а ₀₂ - погонные коэффициенты затухания и фазы, £ ₂ — длина упругой части УЭ.

Соответственно матрица передачи упругой части УЭ записывается в виде:

U 11   U 12

. U 21    U 11 J

chГ shГ

Анализ формул (2) - в ₂ модуль функции Z ba

Re M 11 = 0

минимален, а при

Im T 21 = 0

Z ₀₂ shr ₂

chГ ₂

.

(7) показывает, что при малых значениях коэффициента затухания

(1) при

максимален.

Условие (8), при отбрасывании пренебрежимо малого слагаемого с сомножителем ( в ₂ £ ₂ ) 2 / а ₀₂ £ ₂ , приводит к трансцендентному уравнению

1 - cS tg ^a 0/1 tg ^aо/ 3

tg a 02 1 2 = —Sc ^{03 1} c S -------- ,                                             (10)

^42 tg 01 ^£ 1 +       tg ^a 03 ^£ 3

c ₀₂ S ₁           c ₀₃ S ₂

из решения которого, при известных величинах f ₀₀ , £ 1 , £ 2 , 1 ₃ , С 1 , С ₃ , S 1 , S 2 , и S ₃ , находится скорость звука с ₀₂ в упругой части УЭ. Здесь f ₎₀ — частота, при которой имеет место минимум модуля функции Z b a , индексы 1, 2 и 3 обозначают принадлежность величин к соответствующим участкам.

Величину коэффициента затухания, или коэффициента потерь упругой части УЭ, можно определить одним из двух способов, основывающихся на экспериментальных частотных зависимостях модуля функции Z b _a в окрестности его экстремумов. В этих точках значения модуля функции Z b a , поскольку они определяются только потерями в упругой части УЭ, равны экстремальным значениям модуля входного акустического сопротивления УЭ. Имея это в виду, для оценки его коэффициента затухания можно принять рассматриваемую на рис. 1 установку на участке от точки b до точки 2 за условно однородный волновод. В таком волноводе эквивалентную скорость звука С ЭКВ можно определить по частоте f ₎₀ , при которой имеет место резонанс колебательной скорости (т. е. минимум величины модуля Z_ba ). Поскольку при этом на длине участка от точки b до точки 2 укладывается четверть длины волны, то

Сэкв = 4 f00 £ м , где £ м длина участка от точки b до точки 2.

Из анализа уравнений (2) — (10) следует, что на частоте f ₎₀

в э = 'Zba'm" S2 .

Р ^Сэкв ^£ м

В виду того, что коэффициент затухания и коэффициент потерь связаны соотношением β эК = 2—,

^α 02

то после подстановки (11) и (12) в (13) и, относя потери ко второму участку, имеем

S2 Z a min η 2=

ⁿ P ^f 00 ^£ м

Коэффициент потерь можно определить и обычным путем - по ширине резонансной (по скорости или по давлению) зоны частотной зависимости модуля функции Z_ba , в зоне экстремумов.

Потери в жидкостном тракте трубопроводов обусловлены в основном оттоком энергии в структурный тракт. Коэффициент потерь в структурном тракте является частотно зависимой величиной [5]. Согласно [5], возбуждаемая звуковым давлением вибрация стенок трубопровода, при прочих равных условиях, обратно пропорциональна частоте в степени 0,25. В данном случае, при малых уровнях звуковых колебаний, когда превалирует вязкое демпфирование, т.е. когда потери пропорциональны скорости, можно принять, что коэффициент потерь также обратно пропорционален частоте в степени 0,25:

Ч 2 = Z f ^{4 ,25}. (15)

Постоянный коэффициент £ может быть найден по величине коэффициента потерь на ^{частоте f} ₎₀ или ^f _п.

Таким образом, из измерений модуля функции Zba в окрестности ее экстремума можно определить необходимые для расчета сопротивлений величины — скорость звука и коэффици ент потерь в упругой части УЭ. При известной скорости звука в жесткой (арматурной) части

[ A ] всего УЭ и интересующие акустические сопротивле

можно рассчитать матрицу передачи ния: входного Z11 = 41/A 2, и передаточного Z 21 = 1/ A 21