Расчетные модели для оценки напряженно-деформированного состояния в поверхностном слое деталей при поверхностном пластическом деформировании обкатыванием и выглаживанием

DOI:

Majority of the important parts of machines and mechanisms (parts of the working bodies) are subject to high requirements for the quality of the treated surfaces, determined by a set of geometric, physical, and mechanical parameters: surface roughness, strength and hardness, residual stresses, dislocation density. The required quality of the surface layer of parts can be achieved by finishing-hardening processing, in particular, by surface-plastic deformation (SPD). This type of machining, being the simplest and most effective method of strain hardening, has now proven itself reliably and is therefore widely used in mechanical engineering.

It should be considered that the properties of the part begin to form already at the stage of obtaining the blank (casting, forging, welding, and cutting). The correct choice of material and the method of obtaining the blank greatly affect the dynamic strength of the material, increasing the durability of machine parts [1]. A further increase in the durability of parts in the manufacture is achieved by using various methods of thermal, chemical-thermal treatment, surface-plastic deformation (SPD).

Efficient working of new equipment, characterized by good design and quality of manufacturing, is possible only under optimal operating conditions. With unsatisfactory maintenance, there are sometimes cases of loss of performance even of new machines at the very beginning of operation. Therefore, operational methods are an integral part of a set of measures to increase the reliability and durability of machines [2, 3]. The technological process of manufacturing, assembly and control of products should ensure the required level of quality of the products, including operability and reliability, with the least amount of time and money [4]. All components of the technological process - the processing method and the equipment used, the sequence of operations, tools and processing modes, control methods determine its output parameters and, first of all, the quality indicators of the product specified by the designer in the technical requirements, i.e., its accuracy, quality of the machined surface, mechanical properties and others.

METHODS

The simplest to implement and effective in creating a high-quality surface layer of parts (favorable compressive residual stresses, low surface roughness, depth and degree of hardening) are such methods of finishing and hardening treatment as running and diamond burnishing. Despite the fact that running with slipping occurs when running with a ball in the contact zone, and with diamond burnishing, only sliding occurs, there are similarities between them regarding the nature of the deformation of the surface layer, the ratio of acting forces and friction coefficients, as well as in the patterns of formation of a microprofile of the machined surfaces.

The high quality of the surface layer, achieved by surface-plastic deformation, increases the fatigue strength, contact endurance, wear resistance of parts, and thereby increases the durability of machines and mechanisms [5].

Finishing-hardening processing of parts by rolling and smoothing is characterized by the locality of plastic deformation of the surface layer. Because of the force impact of the deforming body, a deformation zone is created on the contact surface, the initial shape of which corresponds to a dimple, which causes a certain deflected mode along the thickness of the surface layer. Subsequently, as the deforming tool is rolled or smoothed, the entire surface of the cylindrical part is covered with a deformation zone in the form of a continuous helix due to the longitudinal feed, the value of which determines the degree of overlap of the current deformation centers [6, 7].

Because of the local nature of the process of interaction of bodies during surface-plastic deformation, the deflected mode of the surface layer of the part turns out to be inhomogeneous in thickness, i.e. there is an uneven elastic-plastic deformation with its characteristic features: the formation of compressive residual stresses, distortion of the crystal lattice and an increase in the density of dislocations, and an increase in hardness.

RESULTS: CALCULATION MODEL

In order to assess the deflected mode in the surface layer of parts during rolling and smoothing, the following calculation models of loading can be used [8, 9], which differ in the type of load (concentrated or distributed force), the shape and law of load distribution on the boundary of a semi-infinite body:

• 1.    a concentrated force P is applied on the boundary of a semi-infinite body;

• 2.    a uniformly distributed load P is applied within the area of a circle on the boundary of a semi-infinite body;

• 3.    distributed load P0 over the “hemisphere” (proportional to the ordinates of the spherical surface), applied over the area of the circle on the boundary of the semi-infinite body (Figure 1).

The last loading model most accurately reflects the mechanics of contact interaction when a ball is pressed into a semi-infinite body, since the result of this interaction is a plastically deformed zone in the form of a spherical surface. In the direction of penetration (along the z -axis), shear stresses on areas parallel to the coordinate planes are equal to zero (τ xy = τ zx = τ yz =0). Therefore, the normal stresses will be principal.

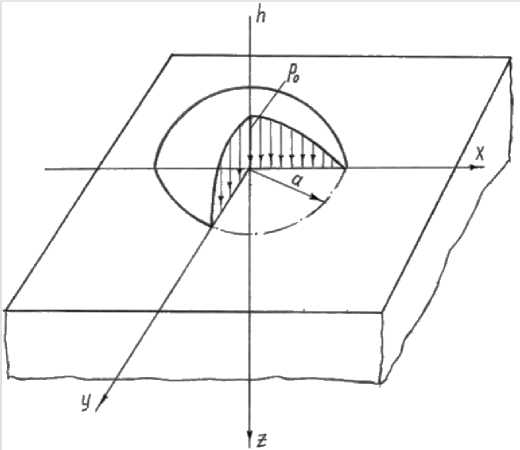
Figure 1. Calculation scheme for the stress state created by a distributed load over the “hemisphere” at the boundary of the semi-infinite body.

The ordinates h of a hemisphere built on this site represent the load distribution P over the area of a circle with a radius:

p

p0

hh

= -p p = p 0 •  = p 0

aa

2  22

a — (x + y )

a

= P 0 Л ¹

-

x + У

a

where, p is the pressure in the center of the circular platform F; p is pressure corresponding to the h ordinate of the hemisphere

The maximum load P will be:

P = Pd)FF = ^ hdF

F          aF      ,

2 where I hdF =

F        ³

n • a ³ is volume bounded by a hemisphere of a radius. Consequently,

P ⁰ = 2 •

P

n • a

Thus, when the load is distributed over the “hemisphere”, the highest pressure is 1.5 times higher than its average value.

The stress components under a load distributed over a circular contact can be determined from the dependencies:

^T Z

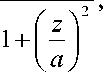
^T Y

= ^T X =

- ^p o ^{[(1 +} Md ^- —

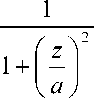
za

— (1 + m )--- arctg —]

az

where z is the distance to some considered point of the surface layer; m is Poisson’s coefficient.

Due to the axial symmetry of the stress state in the case of a circular contact area, we have σ x = σ y . The normal stresses σ x and σ y , in contrast to σ z , depend on the elastic properties of the material (Poisson’s coefficient). If we take z = 0 in formulas (2), then

1 + 2m

tz = — Po";°x = — P0       = ^Y .                     (3)

Because az = гт,;ax =

°i=p-'—w

2 • (1 + -  )

к a J

za

- (1 + ^) • (1---arctg -)]

a

z

.

Given calculation model of loading is applicable for the analytical description of the contact interaction in the shot-impact processing of machine parts for strain hardening. The stress intensity σi calculated by formula (4) allows further determining the level of specific stored energy Us, which is an energy criterion for the quality of the surface layer of parts after final machining and is responsible for the residual stress state. Estimation of the stored strain energy in the surface layer of parts after machining is based on several reasonable approaches that consider the fundamentals of the theory of dislocations, the thermodynamics of irreversible processes, and the energy analysis of the deformation diagram of materials.

CONCLUSION

The reviewed justification for the choice of a calculation model for assessing the stress state during finishing and hardening processing, in particular, during shot-impact, is the most effective processing, since finishing work and hardening properties are considered difficult in practice. The given analytical dependences for calculating the components and intensity of stresses in the surface layer of a semi-infinite body under the action of a distributed load over a spherical surface are calculated to the slightest accuracy, which corresponds to the relevance of this research.