Расчетные процедуры, используемые в обоснование системы требований к материалам конструкций морской техники и магистральных трубопроводов

За расчетный дефект сварного соединения толщиной S принимают поверхностную полуэл-липтическую трещину, ориентированную у границы усиления шва вдоль оси шва, с соотношением размеров l / a = 3. Глубину a принимают в зависимости от примененной процедуры и объема неразрушающего контроля при строительстве конструкции (как максимум, такой дефект не превышает размера валика сварного шва). При наличии конструкции протяженных сварных соединений глубину расчётного дефекта принимают в зависимости от их относительной длины:

a = - 0,14 x S ^0,5ln ( 1 - 0,95 1/ N ) .

Используя величину J -интеграла, сформулируем условие предотвращения хрупкого разрушения в детерминистической постановке:

J c >  n x J ,                                          (1)

где J c – среднее критическое значение J -интеграла по испытаниям при температуре T D , n – коэффициент запаса, J – параметр нагрузки конструкционного элемента с расчётным дефектом. Расчетная процедура используется для определения коэффициента запаса в формуле (1). Поскольку рассматриваются эксплуатационные температуры в интервале вязко-хрупкого перехода, можно считать, что наступление разрушения по хрупкому механизму может произойти с некоторой вероятностью. То же условие прочности (1) в вероятностной постановке имеет вид

( J c ) , ■>( J j                                           (2)

где индексы i и j соответствуют случайным значениям трещиностойкости металла и параметра нагружения элемента конструкции с расчётным дефектом в конкретном случае нагружения.

Главная особенность процедуры – совместный учет нескольких независимых случайных параметров, задаваемых через генераторы псевдослучайных чисел (рандомайзеры) с периодом повторяемости не менее 107. Данный период обеспечивается при количестве значащих цифр переменных не менее 8 в рекурсивных формулах вида xk = {q • xk}, где q - простое число. В число параметров входят:

• •    случайная глубина дефекта a j = - ln ( x 1 ) • a /ln20, что соответствует вероятности того, что

• дефект глубиной более a будет обнаружен с вероятностью 95 %;

• •    распределение случайных относительных напряжений a j = a • ( l - 0,5

  , где a

  
  

  - детерминированная величина относительных напряжений. Показатель степени х = 0,173 выбран таким образом, чтобы обеспечить наступление наибольших нагрузок, составляющих не менее 0,95 a , с периодичностью 5 000 случаев за срок службы 30 лет, или 167 раз в год, предполагая за каждый год 10⁸ случаев нагружения. Доминирующее число случаев нагружения, таким образом, связано с небольшими нагрузками (работа оборудования, перепады давления и т. п.);

• •    температура, соответствующая случаям нагружения, задаваемая усеченным нормальным распределением (УНР), точка среза распределения – абсолютно минимальная климатическая температура в месте дислокации конструкции, T min . Случайное значение температуры эксплуатационного нагружения (до среза распределения) определяется по формуле

Tj = T0 + у/-2ln (x3 ) x cos ( 4п • x4 )• a^), где x3 и x4 - псевдонезависимые случайные величины в диапазоне (0, 1), с(Т) - среднеквадратическое отклонение, °С;

• •    трещиностойкость материала, которую считают удовлетворяющей трехпараметрическому распределению Вейбулла, где в - параметр формы распределения, связанный с коэффициентом вариации V ; J c0 – медианное значение (параметр масштаба), J min – минимальное значение:

( Jc )! = Jmin + (Jc0 - Jmn)[-ln(X5 )]1/в , i TD что следует откорректировать для температуры, соответствующей случаю нагружения:

( J c ) J,= ( J c ) J,_d exp(0,04( T j - T d )) .

• З адают приемлемую вероятность разрушения Q , а также начальное значение J c0 . Количество опытов в численном эксперименте для проверки условия (2) принято равным 2 x 10 6 , что доста-

  Филин В.Ю., Бараков Д.Р., Назарова Е.Д.

  
  

Расчетные процедуры, используемые в обоснование системы требований к материалам конструкций морской техники … точно по результатам проверки зависимости результатов от числа опытов. Вычисляется количество случаев «разрушения», то есть невыполнения условия (2). По результатам расчёта методом пошагового спуска подбирают новое значение Jc0, которое обеспечивает получение задаваемого значения вероятности Q с допуском 5 %. В результате вычисляют частный коэффициент запаса n1 = Jc/ Jmin. Чтобы получить искомый коэффициент запаса n в формуле (1), необходим дополнительный сомножитель nA, учитывающий ограниченность числа корректных результатов испытаний в серии m, то есть возможное отличие Jc от их среднего арифметического значения. Последний, исходя из отдельного численного эксперимента, для случая трёх корректных результатов в серии образцов принимают равным nA = 0,6 + (9V3 - 3,4V2 + V)(0,00031S2 - 0,05S + 6,5).

Окончательно определяют требования к минимальным средним значениям J _c и CTOD. Для выполнения расчётов разработано специальное программное обеспечение. На основании выполненных численных экспериментов предложена формула для коэффициента запаса n в случае, когда максимальная эксплуатационная нагрузка составляет а = 0,7 о т , где с _т - предел текучести стали :

n = ( 1,4 - 6,9V + 30 V ² ) х ( 1 - ( m - 3)/7 х VV ) , n >  1, V > 0,10.

Расчетная процедура в обеспечении второго уровня безопасности. Моделирование распространения трещины при конкурирующем вязком и хрупком разрушении

Если трещина в конструкции стартовала, она должна быть остановлена основным металлом. Способность остановить трещину выражается температурой торможения трещины ( Т _хр) или критическим значением коэффициента интенсивности напряжений (КИН) K _{I a} при этой температуре. Температуру Т хр затруднительно найти прямыми испытаниями, поэтому находят температуры вязко-хрупкого перехода основного металла NDT, Т КБ , T DWTT . Цель расчетных процедур – обоснование корреляций Т _хр с перечисленными температурами. Их использование позволяет получить оценки Т хр по каждому виду испытаний. За T D – минимальную температуру применимости материала – принимают наиболее высокую («теплую») из этих оценок [2].

Температура нулевой пластичности NDT – максимальная температура, при которой происходит разрушение образцов с хрупкой надрезанной наплавкой при ударе падающим грузом. Температура Т КБ при испытаниях на статический трехточечный изгиб образцов натурной толщины с круглым (ключевым) надрезом соответствует средней доле волокнистой составляющей в изломах 70 %. Температура T DWTT при испытаниях на трехточечный изгиб падающим грузом образцов с острым надрезом соответствует доле волокнистой составляющей в изломах 70...85 % [2].

В НИЦ «Курчатовский институт» – ЦНИИ КМ «Прометей» предложена численная модель [3], не связанная с расчетами методами конечных элементов (МКЭ), позволяющая оценить величину K I a , необходимую для торможения распространяющейся по хрупкому механизму трещины в элементе конструкции толщиной S [мм]. Такая оценка составляет

K1 a\T = 73,5X10-5 ./ • S , (3) хр где Tхр - температура торможения трещины, отэ - эффективный предел текучести материала при данной температуре, который, в частности, учитывает упрочнение вследствие повышения скорости деформирования. Требуемая величина K1a судостроительных сталей, определенная по этой формуле, как правило, не превышает 100 МПа-м0,5, поэтому допустимо использование линейной механики разрушения. Оценка требований к температурам вязко-хрупкого перехода, определяемым каждым из применяемых методов, осуществляется с использованием следующей процедуры:

• •    определяется «истинная» диаграмма нагружения материала с пределом текучести с т [3, 4];

• •    с помощью выполнения серий расчетов МКЭ процесса нагружения испытательного образца определяется сеточно зависимая величина жесткости напряженного состояния х , (то есть достигаемая в какой-либо точке фронта трещины и используемая в качестве условия хрупкого разрушения [4–6]

X = ^с 1 / С , где с - первые главные напряжения, а - интенсивность напряжений;

Механика

• •    подбирается х , соответствующее достижению соответствующей температуры вязкохрупкого перехода;

• •    решается калибровочная задача МКЭ, где в условиях плоской деформации и маломасштабной текучести в модели с тем же размером конечного элемента, нагружаемой растяжением ( Y -функция равна единице), создается такая же величина х и определяется соответствующее критическое значение КИН материала K 1 a  = ^/Л а , где Т _г - температура испытания. Данная про-

• Tт

цедура необходима, так как прямое определение КИН для модели образца невозможно, а пересчет через изменение потенциальной энергии ( J -интеграл) дает слишком низкие «средние» значения;

• •    поскольку рассматриваются температуры в интервале вязко-хрупкого перехода, используется ожидаемая температурная зависимость КИН в виде

K ia\_T = K ia\_T • exp [ 0,02 ( T d - T m ) ] .                           (4)

Dт

Формула (4) практически эквивалентна температурной зависимости нижней огибающей K [ _a в коде BPVC [7]. Из нее определяется требуемый температурный запас ( T D -Т т ) с учетом (3).

Для каждого из видов испытаний проводится поэтапное решение упругопластической задачи МКЭ при возрастающем перемещении точек приложения нагрузки вплоть до выполнения какого-либо из принятых локальных условий разрушения. Затем при фиксированных перемещениях выполняется поэтапное снятие запрета на перемещение узлов «разрушенных» элементов относительно плоскости симметрии образца вплоть до прекращения продвижения трещины. После этого нагружение возобновляется. Используются несколько конкурирующих условий разрушения:

• •    хрупкое разрушение по достижении критического значения жёсткости напряжённого состояния х ;

• •    вязкий отрыв по достижению одного из локальных критериев: критической деформации либо нормализованного по величине интенсивности пластической деформации критерия Кок-рофта-Лэтэма-Оха [3],

• •    вязкий срез по достижении критического значения максимальной касательной деформации У с = ( ъ — £ з )/2 [5].

К настоящему моменту получены следующие корреляции:

для испытаний по методике NDT:

Тхр - ТКБ = 50ln ^1,55       -(^т )Т2'/(^т ) т,• для испытаний по методике DWTT:

T DWTT = Т хр - (0...10)°С.

Все представленные оценки сделаны для изотропного металла. Оценки для металла после термомеханической обработки, склонного к расщеплениям, отличаются, для исследования влияния расщеплений создана специальная модель МКЭ.

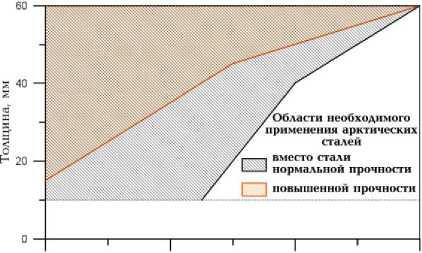
То. "С

Минимальная температура применимости стали «обычных» марок и области необходимого применения сталей с индексом «Arc» для морских конструкций

Филин В.Ю., Бараков Д.Р., Расчетные процедуры, используемые в обоснование системы Назарова Е.Д. требований к материалам конструкций морской техники … О необходимости применения сталей арктических марок

Применение рассмотренных расчетных процедур позволяет оценить минимальные температуры применимости «обычных» марок стали (см. рис.), описанных в Правилах Российского морского регистра судоходства [2]. Оказывается, что эти границы не охватывают соотношения толщин и температур эксплуатации, требуемые для современных арктических проектов. Поэтому предложено внести в [2] требования к применению арктических марок стали (с индексом «Arc») для изготовления наиболее ответственных конструкций – судовых связей категории III и специальных конструкционных элементов морских платформ.

Выводы

Обоснование требований, предъявляемых к судостроительным и трубным сталям, требует применения разнообразных расчетных процедур, связанных как с численными вероятностными экспериментами, так и с моделированием МКЭ процесса распространения трещины при конкурирующем вязком и хрупком разрушении. Разработаны расчетные процедуры, применимые как на стадии аттестации новых материалов, так и для оценки допустимой дефектности.

Для новых морских проектов с высокими эксплуатационными требованиями обоснована необходимость использования сталей с индексом «Arc». Расчетные соотношения критических температур подтверждены экспериментально.