Расчёт и моделирование цифровой робастной системы управления связанным нестационарным объектом

Параметры моделей каналов объекта управления в процессе эксплуатации зачастую претерпевают значительные изменения, при этом большинство технологических объектов являются многосвязными. Разработанные способы управления такими объектами подразумевают изменение настроечных параметров системы с течением времени. Перенастройка требует наличия уточнённых данных о параметрах модели объекта, то есть необходимо проведение текущей идентификации, что не всегда возможно, тем более для многосвязных объектов. Применение же принципов робастного управления обеспечивает гарантированное качество и требуемый запас устойчивости на протяжении всего эксплуатационного периода [1]. В работе поставлена задача разработки, моделирования и исследования робастной цифровой системы управления многосвязным объектом, включающая следующие этапы:

– выбор и обоснование критериев управления;

– оптимизация управляющей части системы по предложенным критериям;

– моделирование системы при возможной вариации параметров модели объекта со связанными параметрами в течение эксплуатационного периода;

– исследование функционирования робастной системы по различным критериям синтеза и оценка эффективности работы по показателям качества и запасу устойчивости.

При синтезе систем регулирования и расчёте оптимальных настроечных параметров цифровых регуляторов наиболее часто применяется критерий минимума интегральной квадратичной ошибки (1). В дискретной форме для многосвязного объекта этот критерий можно представить следующим образом:

nm

S - ЯI f 2 ]             (1)

j = 1 i = 1

где: S 1 – интегральная квадратичная ошибка; e_ij – рассогласование по каналам управления; n – число параметров управления; m – количество точек разбиения переходного процесса.

Вместе с тем, при синтезе робастной системы управления одним из требований является не только обеспечение качества управления, но и достижение требуемого запаса устойчивости, поэтому введём комплексный критерий (2) [2]:

S₂ = tj tj + ^a/p]            ⁽²

j = i i = i             ^p j

P = 1 - ^maI|- где: S2 – комплексный критерий, учитывающий интегральную квадратичную ошибку и запас устойчивости системы; p - запас устойчивости системы;

A max — максимальный корень характеристического полинома канала управления; a j - весовой коэффициент по каналам управления.

Кроме того модифицируем критерий (1), учитывающий качество управления не только при номинальном состоянии объекта, но и в конце эксплуатационного периода, то есть возможный интервал изменения параметров модели объекта:

nmm

S 3 = ВK H ) ' 1 )] (3) j = 1 i = 1 i = 1

где: S₃ - суммарная интегральная квадратичная ошибка в начальном и конечном состоянии объекта; в”^С , ву^С - рассогласование по каналам управления в начальном и конечном состоянии.

В качестве примера многосвязного объекта рассмотрим процесс синтеза аммиака (рисунок - 1) [2, 3].

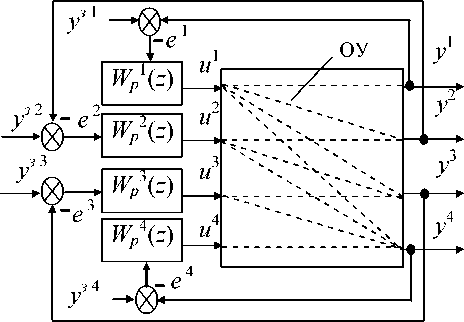
Рисунок 1 - НЦСР процессом синтеза аммиака: ОУ - объект управления; у 1 - у ⁴ - измеряемые выходы системы (температура в слоях катализатора); у³ 1 - У ⁴ - задающие воздействия; е 1 - е ⁴ - ошибки регулирования; u 1 - " ⁴ - управляющие воздействия (степени открытия заслонок на байпасных потоках); W p 1 ( z )- W p ⁴ ( z ) - дискретные передаточные функции цифровых регуляторов.

Нестационарные свойства объекта обусловлены изменением активности катализатора с течением времени [4], в связи с этим рассмотрим возможный диапазон изменения параметров моделей объекта по отношению к номинальному состоянию (Н.С.) в процессе функционировании (таблица 1)

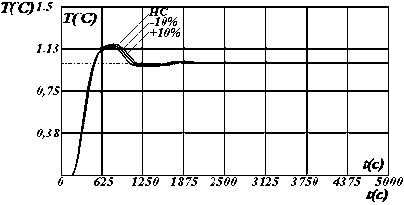
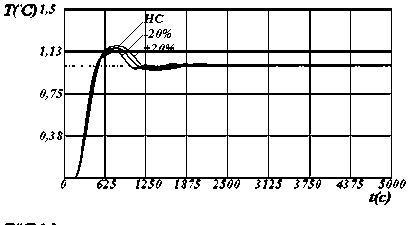
С целью сравнительного анализа робастной системы регулирования, синтезированной по критериям (2,3) с системой, рассчитанной по критерию (1), проведена оптимизация цифровых регуляторов второго порядка по предложенным критериям методом покоординатного спуска. В комплексном критерии S2 большое значение имеет величина весового множителя а, устанавливающего соотношение между запасом устойчи-вости и интегральной квадратичной оценки. Ранее установлено [2], что для данного объ-екта управления при значении а=30 составляющие критерия учитываются в равной степени. Динамические характеристики системы для первых двух выходов (рисунок 1) представлены на рисунках 2,3.

Таблица 1

Изменение параметров моделей каналов объекта в процессе эксплуатации

Состояние системы	Канал	Значения параметров модели ОУ
		Дискретныe
		a 1	b , %мас/(т/ч)	d, такт
-30%	( Wo" [1][1] )	0,859	-0,476	10
	( W o" [2][2] )	0,880	-0,190	16
	( W o" [1][2] )	0,895	-0,062	18
-20%	( W o" [1][1] )	0,877	-0,416	10
	( Wo " [2][2] )	0,895	-0,166	16
	( Wo " [1][2] )	0,908	-0,054	18
-10%	( W o" [1][1] )	0,891	-0,370	10
	( Wo " [2][2] )	0,907	-0,148	16
	( Wo " [1][2] )	0,918	-0,048	18
н.с.	( W o" [1][1] )	0,901	-0,333	10
	( Wo " [2][2] )	0,916	-0,133	16
	( W o" [1][2] )	0,927	-0,043	18
+10%	( W o" [1][1] )	0,910	-0,303	10
	( Wo " [2][2] )	0,924	-0,121	16
	( Wo " [1][2] )	0,933	-0,039	18
+20%	( W o" [1][1] )	0,918	-0,277	10
	( Wo " [2][2] )	0,930	-0,111	16
	( Wo " [1][2] )	0,939	-0,037	18
+30%	( W o" [1][1] )	0,924	-0,256	10
	( Wo " [2][2] )	0,935	-0,103	16
	( Wo " [1][2] )	0,943	-0,034	18

При синтезе робастной системы управ-лeʜия ʜeoбходимо учитывать максимально возможный интepʙaл измeʜeʜия парамeтров объекта управления в процессе эксплуатации. Для исследования изменения динамики системы управления проведена серия численных экспериментов для критерия S₃ (рисунки 4,5). Сравнение предложенных критериев проводилось по показателям качества и корням характеристического полинома системы.

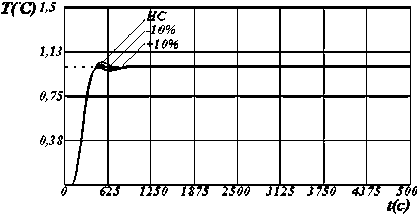
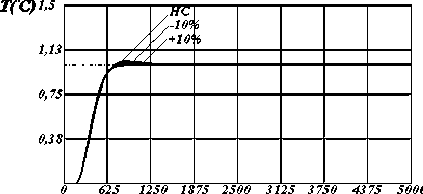
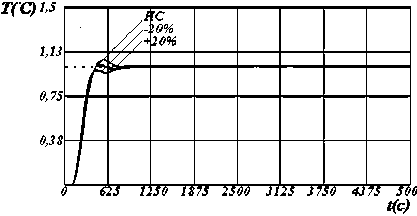
II

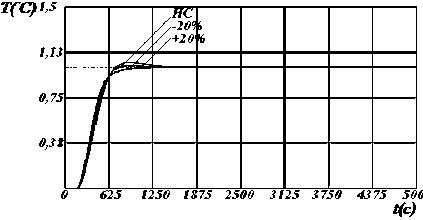
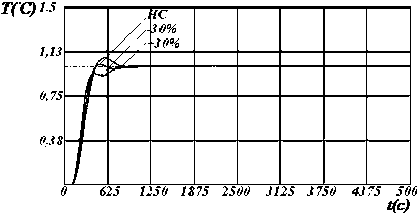
Рисунок 2 - Динамические характеристики системы по у ^[1] с настройками регулятора по критерию S 2 , где: I , II, III - изменение параметров модели на 10%, 20%, и 30% соответственно.

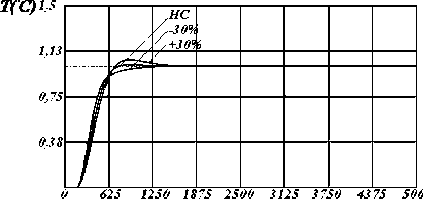
Рисунок 3 - Динамические характеристики системы по у ^[2] с настройками регулятора по критерию S 2 , где: I , II, III - изменение параметров модели на 10%, 20%, и 30% соответственно.

Анализ показателей качества (таблицы 2, 3) динамических характеристик позволяет сделать выводы, что наименьшими ошибками обладает система, синтезированная по критерию S 1 и по S 3 в номинальном состоянии. Комплексный критерий S 2 показал незначительное ухудшение данного показателя: отклонение от лучших показателей не превышает 10%. При этом суммарный интегральноквадратичный критерий S 3 обладает наилучшей стабильностью в процессе эксплуатации, так как изменение не превысило 2,5%.

Наибольший запас устойчивости системы достигается в случае применения комплексного критерия S 2 . Критерии S 1 и S 3 в номинальном состоянии обладают схожими значениями запаса устойчивости. В процессе эксплуатации системы происходит увеличение апериодических запаздываний по каналам модели объекта, что в свою очередь приводит к увеличению запаса устойчивости.

Изменение качественных показателей системы в процессе эксплуатации проявляется для каждого из предложенных критериев, однако разница интегральной квадратичной оценки незначительна (таблицы 2, 3; рисунки 6, 7).

Анализ изменения времени регулирования системы управления позволяет сделать вывод, что наилучшими показателями обладает система, синтезированная по комплексному критерию S₂ по сравнению с S 1 и S 3 (рисунки 8, 9). Для критериев S 1 и S 3 с увеличением срока эксплуатации время регулирования по у [1 уменьшается, а по у [2 увеличивается, тогда как для критерия S₂ значения варьируются незначительно и почти в 2 раза меньшие чем при S 1 и S 3 .

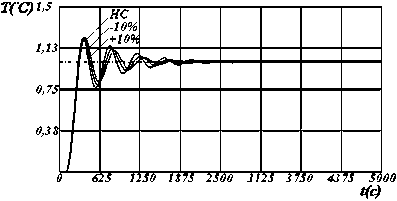
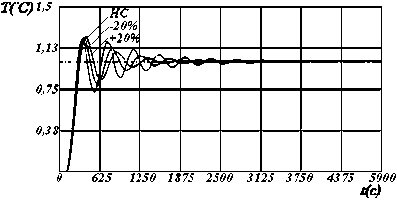
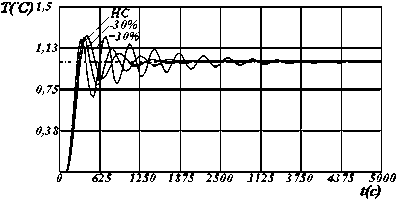
Рисунок 4 - Динамические характеристики системы по у ^[1] с настройками регулятора по критерию S 3 , где: I , II, III - изменение параметров модели на 10%, 20%, и 30% соответственно.

Таблица 2

Изменение интегральной оценки выхода у ^[1] системы для paзличных критериев

Состояние объектa	Πepʙый выход системы
	S 1	S 2	S 3
-30%	18,473	19,823	19,505
-20%	18,515	20,31	18,976
-10%	18,729	20,798	18,925
н.с.	19,033	21,287	19,073
+10%	19,388	21,777	19,323
+20%	19,777	22,267	19,633
+30%	20,188	22,758	19,98

Диʜaмическaя ошибкa для критерия S 2 так же оказались в 2-3 раза меньше значений полученных при ʜacтройке по критериям S 1 и S 3 (рисунок 10).

Оценкa зʜaчений мaксимaльных корней характеристического полинома системы (рисунок 12) для S 2 показала, что при изменении параметров модели объекта от номинальных значений происходит увеличение мaксимaльного корня, что свидетельствует об уменьшении запаса устойчивости. Для критериев S 1 и S 3 наблюдается уменьшение значений корней. Вместе с тем ʜaименьшим по модулю мaксимaльным корнем обладает система, синтезированная по критерию S 2 с весовым коэффициентом а=30 .

II

III

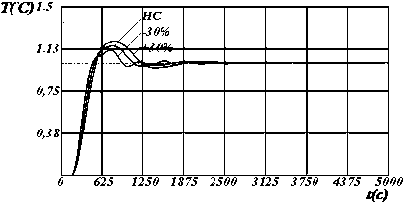
Рисунок 5 - Динамические характеристики системы по у ^[2] с настройками регулятора по критерию S 3 , где: I , II, III - изменение параметров модели на 10%, 20%, и 30% соответственно.

Таблица 3

Изменение интегральной оценки выхода у ^[2] системы для paзличных критериев

Состояние объектa	Bторой выход системы
	S 1	S 2	S 3
-30%	27,863	31,15	27,92
-20%	28,663	31,817	28,687
-10%	29,457	32,478	29,456
н.с.	30,244	33,135	30,221
+10%	31,023	33,788	30,981
+20%	31,794	34,435	31,734
+30%	32,559	35,08	32,481

Таким образом, в результате численного моделирования системы и оценки показателей качества при вариации параметров моделей объектa для paccмотренных критериeʙ ʜaилучшим является комплексный критерий S 2 , обеспечивающий наибольший запас устойчивости системы и достаточно хорошее качество регулирования. А такие показатели как время регулировaʜия и диʜaмическaя ошибкa для критерия S 2 меньше, чем для S 1 , S 3 .

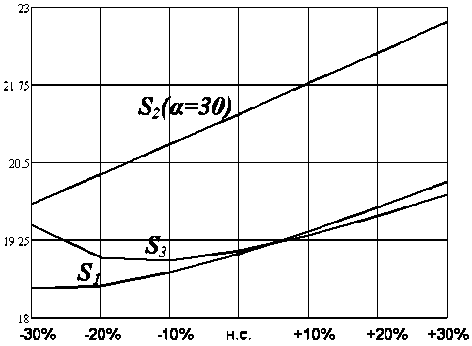
Рисунок 6 - Изменение интегральной квадратичной оценки по у ^[1]

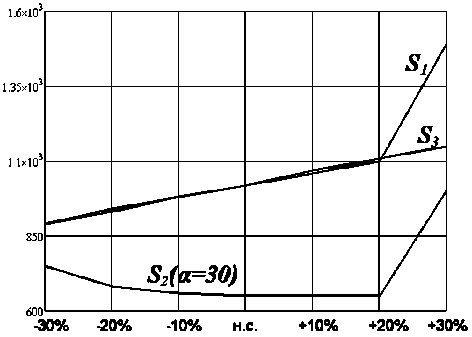
Рисунок 9 - Изменение времени регулирования [2]

системы для у ^{[ ]}

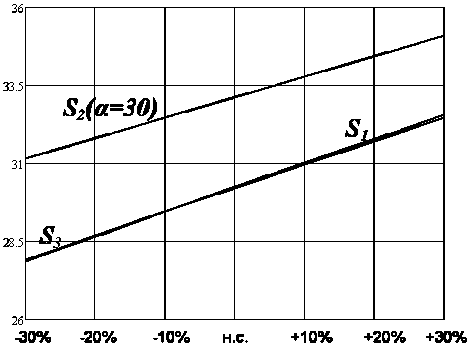
Рисунок 7 - Изменение интегральной квадратичной [2]

оценки по у ^{[ ]}

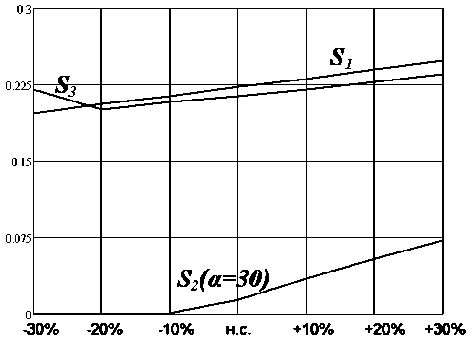
Рисунок 10 - Изменение перерегулирования системы для у ^[1]

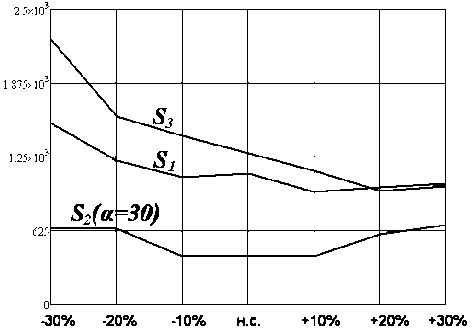
Рисунок 8 - Изменение времени регулирования системы для у ^[1]

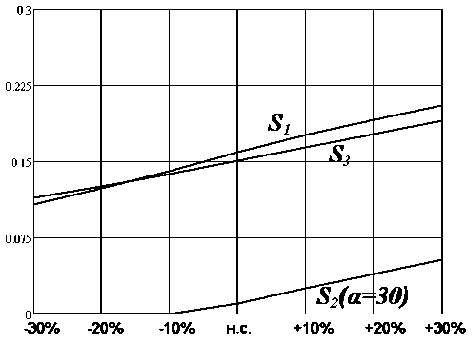
Рисунок 11 - Изменение перерегулирования системы для у ^[2]

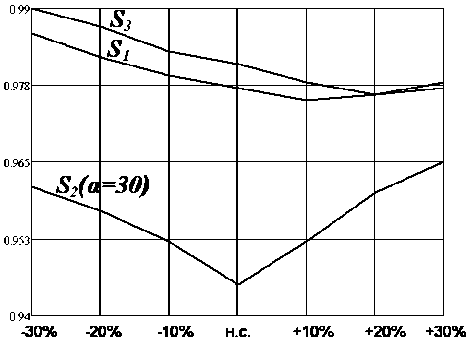
Рисунок 12 - Изменение модуля максимального корня характеристического полинома системы