Расчёт энергетического спектра сложных низкоразмерных гетероструктур в присутствии электрического поля

Исследования в области разработки высокопроизводительных вычислительных систем, средств связи и обработки информации привели к появлению нового подхода в создании элементной базы электроники [1-6]. В рамках этого подхода носителем информации выступает амплитуда электронной волновой функции в данной области квантовой системы. Прикладывая внешнее электрическое поле, меняющее энергетический спектр, можно вызывать контролируемую передислокацию электронной плотности в системе, соответствующую преобразованию информации по заданному закону.

В качестве физической основы для реализации приборов с управляемой передислокацией электронной плотности могут быть использованы структуры, образованные набором туннельно-связанных квантовых ям.

В многоямной квантовой структуре распределение амплитуды волновой функции определяется, по сути, интерференцией квантовых состояний различных квантовых ям, поэтому перераспределение электронной плотности под действием внешнего электрического поля может носить сложный, немонотонный характер. При этом соответствующий немонотонный характер будет носить и изменение физических характеристик системы, что открывает широкие возможности для разработки различных квантовых приборов.

Для создания электронных приборов необходимо научиться целенаправленно управлять энергетическим спектром носителей заряда с помощью различных внешних воздействий. Наиболее часто для управления используют электрические поля. Расчёт энергетического спектра такой системы можно выполнять с использованием стационарного уравнения Шрёдингера с заданной структурой потенциала и приложенным постоянным электрическим полем.

В случае кусочно-постоянной формы потенциала такая задача может быть решена на основе пред ставления волновых функций в виде суперпозиции функций Эйри. Для простых типов гетероструктур, описываемых одним или двумя уровнями потенциала, можно получить аналитическое решение [1,2], однако для сложной формы потенциала задача становится очень трудоёмкой [2]. Как правило, эта проблема решается с помощью метода возмущений [7], но он применим лишь для небольших значений приложенного электрического поля.

Таким образом, актуальной является задача разработки и реализации численного метода расчёта энергетического спектра для сложного профиля потенциала при наличии электрического поля.

В данной работе описывается алгоритм решения соответствующего стационарного уравнения Шрёдингера. Алгоритм основан на последовательной сшивке решений на границах зон без повышения ранга матрицы более двух, что позволяет легко реализовать процедуру поиска корней характеристического уравнения.

Проведено сравнение разработанного алгоритма с методом возмущений.

1.    Алгоритм решения уравнения Шрёдингера на основе метода последовательной сшивки

Рассмотрим одномерную гетероструктуру, соответствующую системе однородных слоёв полупроводников (границы слоёв перпендикулярны оси Ох) в присутствии электрического поля. Если поле напряжённости F направлено параллельно оси х, то потенциальная энергия будет иметь вид:

U (%) = qFx + U_p , (1) где q - абсолютная величина заряда электрона, U_p - значение кусочно-постоянного потенциала на отрезке ге[г г], х - координаты границ слоёв.

В этом случае уравнение Шрёдингера имеет вид:

• -3L ti%)^_qFx+u^ _v(x)=£v(x), ₍₂₎

2т dr ^х '

где т_р - эффективная масса, у(х) - волновая функция частицы.

Обозначим

M=Z7;;/3(.Y-C;1),

(З)

где с_р

E-U_p qF

bp

( 2т pqF )

I й2 )

Тогда волновая функция от аргумента и будет удовлетворять уравнению Эйри:

.                                      (4)

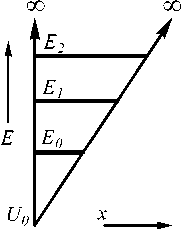
Рис. 1. Энергетический спектр в треугольной бесконечной потенциальной яме

Нормировка константы А_о в (8) производится из условия равенства единице интеграла от квадрата модуля волновой функции.

Условие (8) выполняется при и(х₀) = а_п , где а_п - корни функции Эйри. Таким образом, разрешённые значения энергии имеют вид:

Решение (4) имеет следующий вид на каждом интервале [8]:

V,, («„W) = А_рА^иДх^ + В_рВ1^иДх^ ,       (5)

где Up^xVbpb^x-CpY ^elv?¹,]; Aiy\Bi^ — функции Эйри первого и второго рода соответственно.

Накладывая условия сшивки для волновых функций и их производных, делённых на массу, на границах между различными интервалами (границами слоёв), получим следующие уравнения для коэффициентов в решении (5):

APAiSVuP^ + BPBiSVup-pV

= УэЛ^рМр^ ^Вр₊М“р^Л ^\_^АР^АЧ^ир.рУ^вР^вЧ^ирЛ=          ⁽⁶⁾

= V"W Ai'^.P)+ BppxBi\uppVp)] ’ где “р.^ЬУ^-СрУ

Отметим, что разрешённые значения энергии Е входят в (6) неявно через аргументы функций Эйри в (5). Далее рассмотрим получение характеристического уравнения (уравнение для £) на простом примере бесконечной квантовой ямы и в случае потенциала общего вида в квантовой яме.

Е„ =

х0

^^^^^™

2m0qFA 1/3

Й2 J

qF + U0

Полагая х0 = 0 и используя аппроксимацию для корней функции Эйри [8]

а„ = -[(Зл/8)(4л-1)]"/3,

(Ю)

получим приближённую оценку для энергетического спектра треугольной бесконечной ямы в явном виде (учтён также знак заряда электрона):

Е„ ~

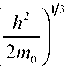
з                   12/3

-?Гл(/7-0,25)

+ ^о ■

(П)

Далее проведём сравнение энергетического спектра в прямоугольной яме конечной ширины в отсутствие и при наличии электрического поля.

3. Бесконечная прямоугольная потенциальная яма

Для ямы шириной 2L потенциал описывается выражением (рис. 2):

2. Треугольная бесконечная потенциальная яма

№) =

=о, хе [-оо,-А],

U₆ + qFx, хе \-L,L\,

Модель треугольной бесконечной ямы использу

ется, например, при описании поверхностного квантования [1,2]. Потенциал треугольной бесконечной ямы описывается выражением (рис. 1):

Ш=

оо, хе [^—°°,х₀], U_Q + qFx, хе [х₀,оо].

о®, хе [Доо].

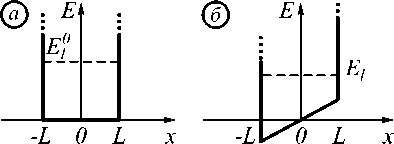
Рис. 2. Прямоугольная бесконечная потенциальная яма в отсутствие (а) и при наличии (б) электрического поля

Граничные условия соответствуют равенству нулю волновой функции (5) на левой границе ямы (при .г = х0 и при х —э оо). Из этого следует, что

В_о=О, и тогда

W₀(«Cr₀)) ⁼ AgAi^u^x^ = 0 ,

, _ч ( Е-иЛ(2тмЕ где ииУ = х₀--—^    (

( qF Д п

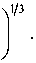
Для классической прямоугольной бесконечной квантовой ямы шириной 2L известно решение:

V„(x) = sin(a„(x+£)),

гДе                         ,

Е„ =

ЯП

2L

й² .. --Н Ug . 2m₀

При небольших значениях приложенного электрического поля можно получить приближённое решение методом возмущений [7].

3.1. Решение уравнения Шрёдингера методом возмущений

Рассмотрим теорию возмущений для невырожденных состояний. Запишем стационарное уравнение Шрёдингера (2) в виде:

^=Jv:«W[v„(x)]dx,(22)

^Х^'К^КИ^’

" "    ^,-Е^    ’

Н[<рл(х)] = Е„<рл(х),                           (15)

где оператор Н имеет вид:

H = H0 + W,                            (16)

W - оператор возмущения, а Но невозмущённый оператор, собственные функции и собственные значения которого определяются уравнениями (13), (14):

е2 = x^l^ww^toidx-e'E1, х

Ь                            J (25)

3.2. Метод возмущений для прямоугольной бесконечной потенциальной ямы с приложенным электрическим полем

В рассматриваемом случае:

Й2 d2

Н_о =--- -+IL, W = qFx.           (26)

2m0 ох

ШмНЧй-

В качестве невозмущённых решений используем (13) и (14). Тогда значения энергии для уравнения (2) вычисляются из выражения:

Разложим искомую собственную функцию возмущённого оператора по собственным функциям невозмущённого оператора:

т

Подставляя (18) в (15), получим:

Х<ШД*)] =

”      ,                                            (19)

т

Умножаем скалярно уравнение (19) на V*(%) и- с учётом ортогональности, получим:

Xc"'j4(x)w[v„,W]dx =

-                                                (20)

= р\Е„-Е»\ I = 1,2,3,... .

Воспользуемся предположением о малости оператора возмущения, тогда энергетические уровни и волновые функции возмущённого оператора будут близки к невозмущённым. Будем искать решение в виде поправок до второго порядка малости:

\е =е° + е' + е2,

' <Р„ W = V„ W + X <^J V™ W ⁺ X ^C™'^m ^Y ^{(2 1 }} т*п             т*н

Из уравнений (20), (21) можно получить следующие выражения для поправок [7]:

еЦ—А —+Ug ₊ E>E², \2L ) 2т₀

где Е\ = qF J sin² (а_л(х + T))xdx = qFL ,

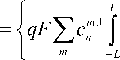
sin(an(x + r))sin(am(x + Z,))xdx-

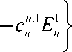
„™.² ^n

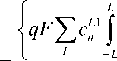
При этом волновые функции определяются следующим образом:

+Х<ЧУ)+Х<Х(х)’ т^п             т^п

где

„тД _

Сп

qF j sin(a_m(x + L))sin(a_n(x + L)^xdx         (31)

1        (е°-Е°\             ’ у и ml

sin (a_m (x + L) ) sin ( a., (x + L)) x dx - c™¹¹ E\

kE"-E^

В первом порядке приближения все разрешённые уровни энергии в бесконечной яме смещаются на одинаковую величину qFL , а во втором порядке приближения зазор между дном квантовой ямы и основным состоянием будет уменьшаться пропорционально квадрату напряжённости электрического поля (смотри, например [1,2]).

Метод возмущений можно применять, пока максимальное значение изменения потенциала на краю ямы под действием электрического поля не станет соизмеримым с величиной энергии состояния [1,2]. Если значения приложенного электрического поля становятся большими, то нужно использовать алгоритм прямой сшивки, описанный в разделе 1.

• 3.3.    Метод сшивки для прямоугольной бесконечной потенциальной ямы

с приложенным электрическим полем

Граничные условия определяются из равенства нулю волновой функции (5) на границах ямы:

Vo k^u-L) = AgAi^u__L ) + B₀Bi[u__L ) = 0,

Vo ^L) = A6Ai^uL) + B0Bi^uL) = 0, где

I qF Л Й J

_( Е-иД(ЪподР^

U, — L------- .

I qp a J

Таким образом, получаем однородное уравнение

Ai^u_L)

NMJ Bi^u^j^Bj которое имеет нетривиальное решение, если детерминант равен нулю:

Ai(u_L }Bi(uL) - Ai(uL ^Bi^u_L) = 0 .(34)

Это уравнение определяет собственные значения Е_п.

Коэффициент Во выражается через Ад с исполь зованием одного из двух уравнений в (33):

80=-А0

Sz(M_J °8z(MJ

W =

а значение коэффициента А_о определяется из условия нормировки волновых функций.

Сравним решения, полученные двумя различными методами.

• 3.4.    Сравнение результатов расчёта двумя методами

  В расчётах использовались следующие параметры: m_o=O,lm_e, т_е = 9,10938188x10 ³¹ кг - масса электрона, К = 1,054571726(47)Х10"³⁴Дж-с - постоянная Планка, потенциал U и энергия Е используются в электрон-вольтах (1эВ = 1,602176487(40) х 10 ^rJ Дж ), электрическое поле задавалось в приведённых величинах. В данном случае U_o = 0 , ширина ямы 27 = 2 нм .

4. Бесконечная прямоугольная яма с кусочно-линейным потенциалом общего вида

В табл. 1 приведены значения трёх первых разрешённых состояний энергии для прямоугольной бесконечной ямы в отсутствие электрического поля, а также при слабом и «сильном» (т.е. когда напряжённость поля превышает значение основного энергетического уровня) электрическом поле.

Как видно из табл. 1, в присутствии сильного электрического поля метод возмущений приводит к некорректным результатам. Результаты, полученные методом сшивки, показывают уширение запрещённых зон между энергетическими уровнями с ростом значения приложенного поля, причём наличие сильного электрического поля приводит к уменьшению зазора между дном квантовой ямы и основным энергетическим состоянием.

На рис. 3 показаны первые три волновые функции, полученные в отсутствие электрического поля, а также при слабом и сильном электрическом поле, рассчитанные методом сшивки. Согласно рис. 3, вероятность нахождения электрона в яме с ростом электрического поля перестаёт быть симметричной и смещается к одной из границ ямы.

В общем случае потенциал в бесконечной потенциальной яме в присутствии электрического поля описывается выражением:

°°, хе [-=,-/.],

U₀ + qFx, хе [-£,х₀],

. . •

Up + qFx,xeVxp_v,xpA,

. . •

U_N + qFx, хе [х.^,7], о°, хе [£,°о].

Таблица 1. Энергетический спектр (первые 3 значения) для прямоугольной ямы

	Отсутствие поля	Поле qF = 0,1		Поле qF = 2
		Метод возмущений	Метод сшивки	Метод возмущений	Метод сшивки
Е,	0,938357	1,037995	0,939758	2,755581	0,761992
Е,	3,753428	3,853667	3,761011	5,810891	3,809982
Е3	8,445214	8,545637	8,462048	10,576528	8,494495

У/Й"

а)

б)

в)

Рис. 3. Волновые функции для бесконечной ямы (в отсутствие поля - пунктирная линия, при qF = 0,1 - точечная линия, при qF = 2 - сплошная линия) для п = 1 (а), п = 2 (б) и п= 3 (в)

В крайних зонах должны выполняться условия равенства нулю волновой функции (5) на границах ямы:

А_оА1^_^+В_оВ1^и_^ = О, ^z(hJ + S_vSz(_MJ-0,

а во внутренних зонах - условия сшивки (6):

AiV*p^

тр

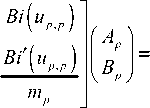
^Aik^l,p^ ^%мр! ^т,м

Bi(uP^.p) ^%^Д.

лр+1

Вр-

нако при этом необходимо использовать «экспоненциальную арифметику» (арифметика над числами, представленными в виде а ехр(й), а и b - параметры числа). Без применения этой арифметики программная реализация работает некорректно при малых значениях электрического поля qF-Fys.

На рис. 4 показан потенциал сложной формы в отсутствие и при наличии электрического поля. В табл. 2 приведены соответствующие значения энергетического спектра для такого потенциала, а на рис. 5 - распределения волновых функций.

Результаты расчёта показывают, что форма потенциала и вариации внешнего электрического поля позволяют существенно менять энергетический спектр и распределение вероятности нахождения частицы в определённой области гетероструктуры.

где аргументы и ,, u__L, u_L определены в (3).

Коэффициенты в последней зоне (последнем слое) можно выразить через А_о и В_о в виде:

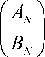
Q

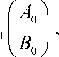
Н1,р^

Qp =

где

х

А’М

X

mP+l         mP-i

AiVup.p^ В%^

mp mp _

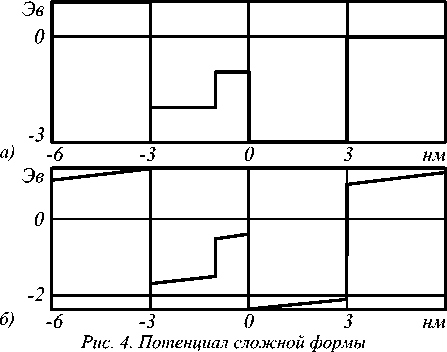
в отсутствие электрического поля (а).

а также при его наличии qF = 0,1 (б)

Таким образом, для коэффициентов Ад, В_о, А„ , B_N имеем 4 уравнения (36), (37). Данные уравнения образуют однородную систему линейных уравнений. Условие равенства нулю определителя этой системы даёт характеристическое уравнение для определения собственных значений Е.

Алгоритм (36)-(38) последовательной сшивки решений на границах зон с использованием матрицы второго ранга позволяет получить характеристическое уравнение в удобной форме.

Численная реализация алгоритма (3б)-(38) обеспечивает простое решение стационарного уравнения Шрёдингера (2) со сложным потенциалом (35). Од

Таблица 2. Энергетический спектр (первые 9 значений) для сложного рельефа

	Отсутствие поля	Поле ?Г = 0,1	Поле qF = 1 Эв
Е„	-2,741001 -2,000144 -1,577124 -0,900418 -0,355715 0,305344 0,660222 1,210436 1,492179	-2,602847 -1,883931 -1,733931 -0,851777 -0,422565 0,493440 0,833417 1,425745 1,979392	-3,705108 -3,295242 -2,376165 -1,857336 -1,647189 -0,779213 -0,338370 0,357965 0,942955

а)

б)

в)

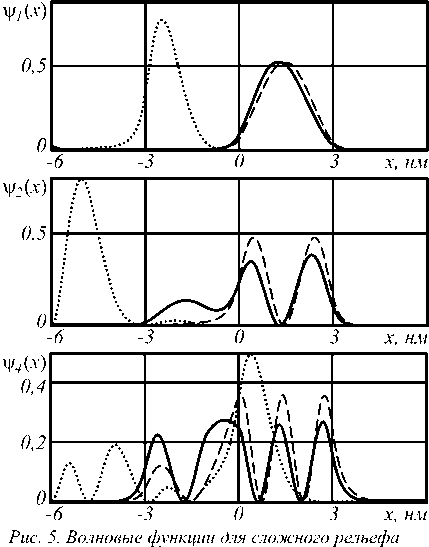
(в отсутствие поля - пунктирная линия, при qF = 0,1 - сплошная линия, при qF = 1 - точечная линия) для п = 1 (а), п = 2 (б) ип = 4 (в)

Заключение

Разработан и программно реализован алгоритм решения стационарного уравнения Шрёдингера для сложного кусочно-постоянного потенциала при наличии электрического поля. Алгоритм основан на последовательной сшивке решений в виде функций Эйри на границах зон без повышения ранга матрицы более двух, что позволяет получить характеристическое уравнение в удобной для поиска корней форме.

Численно показано, что разработанный алгоритм позволяет получать корректные решения при значениях приложенного электрического поля, превышающих величину основного энергетического уровня, т.е. в условиях, когда не применим метод возмущений.

Результаты расчёта со сложным распределением потенциала показывают, что форма потенциала и величина внешнего электрического поля позволяют существенно менять энергетический спектр и вероятность нахождения частицы в той или иной части гетероструктуры.

Работа выполнена при поддержке грантов РФФИ 10-07-00109-а, 10-07-00438-а, 11-07-00153-а, гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9, а также государственных контрактов 07.514.11.4060, 07.514.11.4055.