Расчёт оптической системы с коллиматором для формирования заданного распределения освещённости

Задача расчёта формирования заданного распределения освещённости является актуальной, так как модели оптических систем имеют широкое применение, включающие расчёт светотехнических устройств, расчёт лазерных систем фокусировки, систем навигации, систем безопасности, аварийного, жилого и промышленного освещения, а также систем оптического прицеливания (коллимирования). С математической точки зрения, задача расчёта преломляющей поверхности для формирования требуемого распределения освещенности является обратной задачей (прямой задачей является расчёт освещённости). В общем случае, в приближении геометрической оптики, обратная задача формирования заданного распределения освещённости сводится к решению нелинейного дифференциального уравнения типа уравнения Монже-Ам-пера [1] и является крайне сложной.

Методы решения данного уравнения известны только для случаев радиальной и цилиндрической симметрии.

ной диаграммы направленности при компактном источнике излучения. В работе [4] рассчитывается оптическая система с коллиматором для формирования цилиндрического волнового фронта, однако в ней, как и в работах [5-7] не приведен расчёт аналитической освещённости от полученного волнового фронта.

В настоящей работе рассмотрен случай формирования коллиматором плоско-параллельного волнового фронта. Данный подход позволяет применить для расчета оптического элемента, формирующего требуемую освещенность в области наблюдения, градиентный метод расчёта эйконала, описанный в работе [8]. В качестве примера в работе приведен расчет оптического элемента для формирования распределения освещенности в виде прямоугольника.

ОПИСАНИЕ И КОНСТРУКЦИЯ ОПТИЧЕСКОГО ЭЛЕМЕНТА

Для того чтобы сформировать плоскопараллельный световой пучок круглого сечения, предлагается использовать конструкцию оптического элемента, схема сечения которого изображен-но на рис. 1 [3].

Точечный (компактный) источник света находится в начале координат и излучает свет в полусферу z >0.

Поверхности получены вращением профиля на рис. 1 вокруг оси Oz и предназначены для формирования плоского волнового фронта в плоскости на выходе из коллиматора.

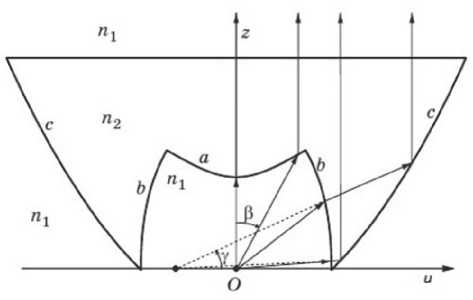
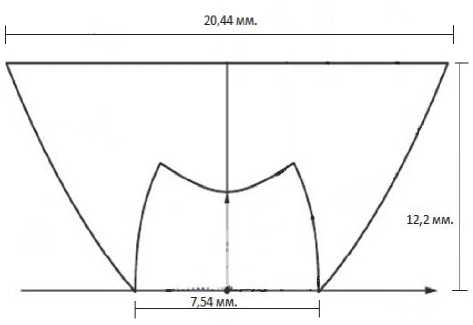
Рис. 1. Схема сечения оптического элемента плоскостью Ouz

^ 0 = r ( Р ) - n^ S + r b ( Р ) + 2 l,r_b ( Р ) sin Р . (2) где r b ( Р ) - длина радиус-вектора средней части b профиля на рис. 1, представляющего собой эллипс; l s – расстояние от источника до мнимого фокуса.

Константа Ψ₀ в выражении (2) выбирается из условия совпадения частей профиля а , b в точке стыковки. Согласно условию (2), расчёт r ( Р ) сводится к решению квадратного уравнения, что приводит к формуле:

r b ^{( Р )} =

T + n²l sin Р 0 s

1 - n

n_xI T 2 + 2T l sin Р - n ² l ² cos² Р + l ² 00 sss

1 - n

Коллимирующий (собирающий) профиль на рис. 1 состоит из трех частей: центральной ( a ), средней ( b ) и боковой ( c ). Центральная часть коллимирует лучи от источника. Средняя часть формирует смещенный мнимый источник, уменьшая угловой размер пучка, падающего на боковую поверхность элемента. Боковая поверхность работает по принципу полного внутреннего отражения и формирует коллимированный пучок, распространяющийся вдоль оси Oz .

Приведенная конструкция оптического элемента является эффективной только при формировании освещённости с большим угловым размером. Это связано с ростом френелевских потерь и явлением полного внутреннего отражения, возникающих при использовании внешней преломляющей поверхности для поворота лучей на большой угол. [9]

РАСЧЁТ ПРОФИЛЯ КОЛЛИМАТОРА

Боковая часть с профиля является параболой, фокус которой совпадает с мнимым источником. Длина радиус-вектора точки параболы относительно точки мнимого фокуса определяется как:

rc ( у) =

2r

0 c

1 - sin у ’

где r_0c – расстояние от мнимого фокуса до пересечения с осью Ou ; у - угол между вектором, проведенным от мнимого фокуса к точке поверхности, и осью Ou .

РАСЧЁТ ОСВЕЩЁННОСТИ, СФОРМИРОВАННОЙ КОЛЛИМАТОРОМ

В аналитическом виде известны выражения для каждой из длин радиус-векторов коллиматора. Формула расчёта освещённости[4], E ₀( u , v ) на плоскости представляется в виде:

Для формирования плоскопараллельного волнового пучка круглого сечения необходимо рассчитать коллимирующий профиль на рис. 1 [3].

Центральная часть а профиля на рисунке 1 является поверхностью коллимирующей линзы. Фокус линзы совпадает с источником излучения. Выражение для длины радиус-вектора центральной части a получаем из принципа Ферма в виде:

Eo U,, v) = Hu, v)^^

0 ( ^ ( ’ d dS ,

где координаты ( u, v) – это декартовы координаты, которые получены при помощи преобразова-

ний:

u = r СОзР _т, к

. R, I(u ’v) v = r SinР

интенсивность то-

г (Р = г ---—- a0a

cos Р — ’

n

чечного источника излучения; d Ω – элементарный телесный угол, в который излучает источник; dS – элементарная площадь коллиматора, на которую падает энергия, излученная в телесном угле d Q .

По определению телесного угла:

где r_0a – расстояние от источника до точки пересечения оптической оси и поверхности линзы.

Средняя часть профиля b должна создавать мнимый источник излучения. При расчёте части b также используется принцип Ферма, согласно которому значение функции:

d Q =----------cos a,        (5)

| OM (u, v )|

где M – это вектор-функция, задающая поверх-

ность,

dM

dM (u, v )xz dM (u, v ) du X dv

dS – эле-

мент площади оптической поверхности, где –

ЭM (u, v) ЭM (u, v))

---------X--------- I - векторное произведе-

Э u        Э v   )

ния для радиус-векторов в прямоугольные координаты. Получаем выражения компонент вектора нормали первой поверхности M 1 ( u , z ) :

ние векторов; а - угол между вектором нормали к поверхности n ( u , V ) и вектором от источника излучения до точки на оптической поверхности OM ( u , V ) ; n ( u , V ) - вектор нормали к оптической поверхности.

Вектор нормали n ( u , V ) по определению, равен:

Э M 1 ( u , z )

Э u

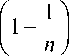
sin ^ cos Р

2 r ( u , z )

cos Р -

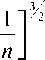
- sin Р

,(10)

n ( u, V) =

ЭM (u, v ) ЭM (u, v )

Э u       Э v

ЭM (u, v ) ЭM (u, v )

Э u       Э v

Э M , ( u , z )

Э z

1 - — | sin ² Р n )

- cos Р

2 r ( u , z )

cos Р -

, (11)

Тогда, подставляя (5) в (4), получим следующее выражение для расчёта освещенности в плоскости наблюдения:

где r ( u, z) = uu2 + z2.

Аналогичным образом считается выражение компонент вектора нормали второй поверхности M ₂ ( u , z ) :

E 0 ^{( u} , ^V ) = I ^{( u} , ^V )

Э M ( u , v ) Э M ( u , v )

-------X-------

Э u         Э v

OM ( u , v ) ²

cos а , (7)

Э M ₂ ( u , z ) Э u

nl cos2 Р s r (u,z)[1 - n2 ]

^{( n -}

(n (u, v ), OM (u, v )) где cos а =         ----------г-.

n (u, V) OM (u, V )

T + n ² 1 sin Р

0 s

J T² + 2T 1 sin Р + 1 ² - n ² 1 ² cos² Р 00 sss

) - sin Р ,

РАСЧЁТ ОДНОМЕРНОЙ ОСВЕЩЁННОСТИ, СФОРМИРОВАННОЙ КОЛЛИМАТОРОМ

В силу того, что профиль обладает радиальной симметрией, можем перейти к расчёту одномерной освещённости. Двумерную освещённость получим в результате полного вращения одномерной освещённости на плоскости.

fax A

r (u, z)    ( \

, n (u)r (u, z )

E0 (u) = I (u) ----------2---- cos а , (8)

r (u, z)

где r ( u , z ) - расстояние от источника до точки на оптической поверхности.

Выражение для вектора нормали n ( u , V ) в точке ( u i , z i ) выражается в частных производных и примет вид:

< ЭM (u,, z ,) ЭM ( u;, z ,) , х -     Эz     , Э u

n ( u ) = -7----------------------------------i k ' < ЭM (u,, z,) ЭM (u,, z,)

-    Э z    , Э u

Найдем компоненты вектора n ( u ) для поверхности M 1 ( u , z ) , задаваемой радиус-вектором г( Р ) по формулам (10) - (11), переводя выраже-

Э M ₂ ( u , z )

Э z

- nl, sin Р cos Р

2^{( n} r ( u , z ) 1 1 - n I

T + n ² 1 sin Р

0 s

_xI T 2 + 2T, l sin Р + l ² - n ² 1 ² cos² Р 00 sss

) - cos Р .(13)

Подставляя выражения (10)-(13) в (9), а затем в (8), получим освещённость, распространяемую в плоскости наблюдения. Так как профиль а представляет собой линзу в фокусе которой находится точечный источник, то пучок световых лучей, выходящих из этого источника, после преломления на профиле станет коллимированным. В случае частей b , c нужно учесть преломление света в соответствии с законом Снеллиуса.

Рассмотрим ход лучей, попавших из источника на поверхность b . Преломлённый луч света должен пересечь среднюю поверхность и затем, отразившись от внешней поверхности, попасть на плоскость наблюдения. Так как мы не учитываем френелевские потери, то точки на поверхности b “перейдут” без потерь в некоторые точки на поверхности c . В частности для ламбертова источника излучения I ( u ) = 1 ₀ cos Р и положив 1 ₀ = 1, можно построить зависимость E ₀ от координаты u . На рис. 2. представлена рассчитанная нормированная освещённость.

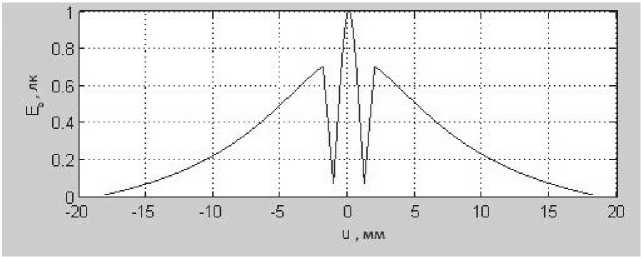
Рис. 2. Зависимость освещённости E₀ от координаты u

ПРИМЕР РАСЧЁТА ЭЙКОНАЛА ДЛЯ ФОРМИРОВАНИЯ ОСВЕЩЁННОСТИ В ВИДЕ ПРЯМОУГОЛЬНИКА В СИСТЕМЕ С КОЛЛИМАТОРОМ

Пусть задана оптическая система, состоящая из точечного источника в начале координат и коллимирующего элемента, размеры которого представлены на рис. 3, с коэффициентом преломления материала n = 1,5.

Данный коллиматор формирует освещенность E ₀, которая была представлена ранее, в плоскости z ₀ . Плоскость формирования требуемой освещённости расположена на расстоянии f = 200 мм от плоскости, в которой расположена апертура. Требуется рассчитать эйконал светового поля, формирующий требуемое распределение освещённости в форме прямоугольника со сторонами 74 мм и 64 мм.

Для расчёта эйконала ф ( u , V ) применим метод, основанный на градиентном методе минимизации функционала ошибки е ( ф ) , который представляет собой отличие расчетного E ( X , у; ф ) и требуемого E ( X , у ) распределений освещенности [8]:

е (ф ) = jj (E (x, У ;Ф^~ E (x, У)) dxdy. (14)

D

Освещенности нормированы по всей излучаемой источником энергии.

В табл. 1. приведены результаты работы применения градиентного метода для минимизации функционала невязки методом Ньютона.

Значения энергетической эффективности и среднеквадратичной ошибки формирования требуемого распределения освещённости при этом равны: e = 0,8321 и х = 0,1102 . Сравнение распределения освещённости в области фокусировки, формируемого в случае рассчитанного эйконала и наперёд заданного распределения, приведено на рис. 4.

ЗАКЛЮЧЕНИЕ

В работе получены следующие результаты:

• -    представлена оптическая система для формирования требуемого распределения освещённости, содержащая коллиматор;

• -    впервые получено аналитическое выражение для освещённости, сформированной коллиматором;

• -    для полученного аналитического распределения освещенности применен градиентный метод расчета эйконала в оптической системе с коллиматором для формирования требуемого распределения освещённости в виде прямоугольника. С энергетической эффективностью e = 0,8321 и среднеквадратичным отклонением ошибки X = 0,1102 .

Таблица 1. Результат минимизации функционала ошибки е ( С )

Ном ер итерации, i	Значение функционала ошибки е ( С )
1	1381,000
2	244,683
3	35,790
4	5,935
5	1,826
6	0,900
7	0,530
8	0,216
9	0,163
10	0,110

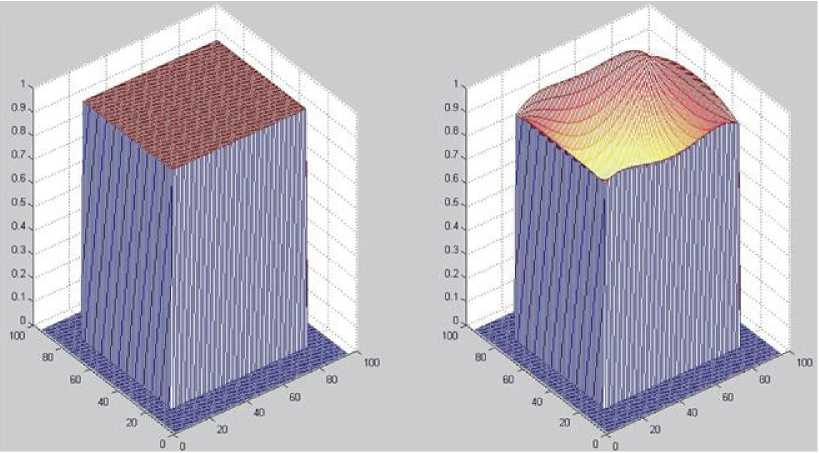
Рис. 4. Сравнение распределения освещенности, сформированного в области фокусировки и заданного

Работа выполнена при поддержке РФФИ (грант 12-07-31193 мол_а).