Расчёт подъёмной силы газового потока в плоском предохранительном клапане с использованием численных методов

При поддержании постоянного давления в ёмкости с помощью предохранительного клапана плоского типа часто наблюдаются повышенный тональный шум и вибрация. Так, при испытаниях дозирующее-предохранительного клапана (ДПК) системы наддува бака периодически возникал повышенный шум струи стравливаемого воздуха с частотами основного тона 100, 200 и 400 Гц. На протяжении всех испытаний наблюдались хлопки с периодичностью 2…5 Гц. Отсутствие периодических источников колебаний показывает наличие автоколебательного режима работы в таких системах.

Обзор работ [1-11], посвящённых исследованию динамических процессов в регуляторах давления, позволил выявить различные механизмы возникновения в них автоколебаний:

• -    струйно-инерционный механизм;

• -    турбулентность;

• -    акустический резонанс.

Каждый из механизмов имеет определённую физическую природу и собственное математическое описание.

Струйно-инерционный механизм так называется ввиду того, что для его появления необходимо наличие связного высокоскоростного потока через отверстие клапана при малом открытии. Когда клапан движется, струя создаёт

импульс, тем самым, изменяя действующую на клапан силу. Инерция потока вызывает гистерезис в этих силах, в результате чего энергия передаётся конструкции, сохраняя её движение.

Рассмотрим статическую характеристику обратных, тарельчатых, конических клапанов (рис. 1). Если обозначить располагаемый гидростатический напор, действующий на клапан Δ H , эффективную площадь клапана A v , плотность жидкости γ , статическое усилие на закрытие будет равно γ ⋅ A v ⋅ Δ H . Для любой данной величины жесткости пружины k , первоначального открытия клапана x₀ существует баланс сил:

kx₀ = γ A_V Δ H . (1)

При значениях подъемной силы меньших kx₀ (1) клапан будет закрыт, а при больших – открыт. Однако при наличии потока разность давлений является динамической из-за высокой скорости потока и его ускорения или замедления при движении заслонки. Поэтому около статических характеристик клапана возникают об-

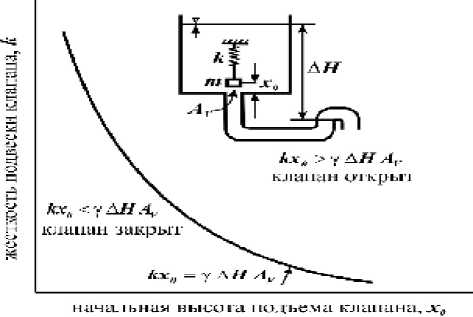
Рис. 1. Статическая характеристика пробкового клапана

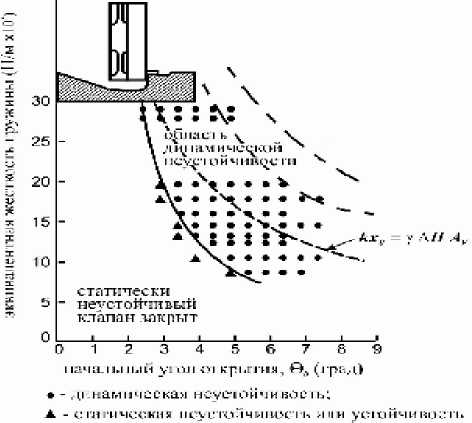
Рис. 2. Область устойчивости поворотного клапана

ласти динамической неустойчивости (рис. 2). В зоне неустойчивости выше статической кривой инерция потока, связанная с уменьшением расхода, вызывает динамическое усилие, закрывающее клапан. Когда поток замедляется, динамический перепад уменьшается, и пружина может открыть клапан (этому способствует и волна низкого давления). В динамической зоне ниже статической характеристики располагаемого статистического перепада вполне достаточно, чтобы удерживать клапан закрытым. Однако внезапное закрытие клапана вызывает волны давления в потоке жидкости, и это приводит к движению клапана от седла и восстановлению течения, – клапан продолжает открываться.

В зоне статической неустойчивости силы упругости недостаточно, чтобы удерживать клапан открытым против сил потока, – клапан закрывается и остается закрытым. Более подробно это описано в работах [1, 2].

Вибрации, вызванные турбулентностью, наблюдаются в клапанах, используемых для регулирования расхода, таких как диафрагменный однолинейный регулятор. Турбулентные пульсации давления, также как прямое воздействие потока на инерционные части клапана могут вызывать разрушительные механические вибрации. В работе [3] установлено, что спектр возбуждающих сил относительно плоский до 100 Гц и в определенных конструкциях может иметь размах колебаний силы более 4,45 кН. Таким образом, клапан регулятора может входить в высокоамплитудные колебания. Более распространены вибрации, связанные с поперечным движением заслонки между уплотнительными или направляющими поверхностями. Они обычно не превышают 1500 Гц, и их звук напоминает металлический дребезг [4]. В результате разбивается седло, направляющие и уплотнения.

По немногим опубликованным экспериментальным данным, широкополосные колебания давления должны иметь существенный уровень энергии до высоких частот. В работе [4] сообщается, что гибкие детали клапана, такие как уплотняющие кольца шарового клапана, клапан с полой юбкой могут резонировать на собственной частоте.

Зарегистрированы тоны от 3000 до 7000 Гц, которые могут приводить к усталостным разрушениям.

При акустическом резонансе в присоединенной трубопроводной цепи происходит усиление пульсаций давления. Во многих случаях, представляющих практический интерес, проблемы возникают на собственной частоте или на низких гармониках колебаний. Поэтому длина волны велика, и возмущения распространяются как почти плоские волны вдоль трубы. Это может сочетаться с изгибными колебаниями трубы и приводить к сильнейшим вибрациям трубопроводной системы. Такие проблемы привлекли внимание из-за серьезных вибраций в паропроводе ядерного реактора, где источником возбуждения, очевидно, был управляющий клапан [5]. Однако, заметных колебаний самого клапана обнаружено не было.

Рассмотрим вибрации клапана, возбуждаемые акустическим резонансом в трубе. Это наблюдается в основном в пробковых и золотниковых клапанах, которые колеблются и действуют, как волновые усилители на границах трубопровода. Примеры показаны на рис. 3.

В обоих случаях пробкового и золотникового клапанов вибрации усиливаются, если акустическая частота трубы близка к собственной частоте клапана. Система особенно неустойчива, если эти частоты совпадают, т.е.

nc ^{f n =} 4l ^,

где f_n - собственная частота клапана;

n – целое число;

с – скорость распространения волн в трубе;

l – эффективная длина трубопровода.

Судить о присутствии автоколебаний при взаимодействии потока с клапаном можно по виду статической силовой (нагрузочной) характеристики, показывающей зависимость подъёмной аэродинамической силы от высоты подъёма тарели над седлом.

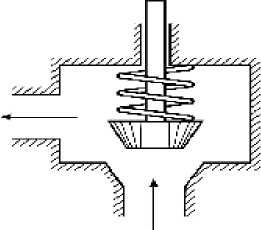
В инженерных расчётах считается, что тарель поднимается под действием постоянного давления p ₁ , равного давлению в ёмкости. Поверхность, на которую воздействует это давление, ограничена диаметром d _расч равным среднему значению между наружным и внутренним диаметром седла (рис. 4)

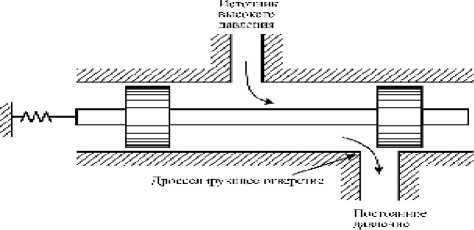
Рис. 3. Схемы золотникового и пробкового клапанов

dс dv расч 2    •             (3)

Давление на поверхность между d_с и d _расч считают равным давлению окружающей среды p₂ и в расчётах не учитывают. Подъёмная аэродинамическая сила определяется соотношением

Р ст = ’^ df⁴- (p i - P a ) .     (4)

Считается, что её величина неизменна с вы- сотой подъёма клапана вплоть до x = — d . В 4v этом случае статическая характеристика аэродинамической силы по высоте подъёма представляет собой ступенчатую функцию (рис. 5).

Очевидно, что такое сочетание подъёмной силы и силы упругого противодействия тарели приводит к установлению устойчивого равновесного положения на уровне высоты подъёма, соответствующего точке пересечения силовых линий и исключает автоколебательный режим. С подъёмом из-за ускорения потока происходит изменение давления в зазоре между клапаном и седлом. Это оказывает существенное влияние на вид статической характеристики подъёмной силы. Помимо сил статического давления на та-рель воздействуют активные и реактивные силы стравливаемого потока газа [8-11]:

„ Р "  W ²

^Рдин = F эф " ^V "  2 ’ ⁽⁵⁾

где F эф – эффективная площадь тарели на которую оказывает воздействие струя; V — коэффициент, учитывающий реактивное действие

Р- w2 струи в направлении подъёма тарели;       – скоростной напор. Величина V зависти от угла выхода среды из щели. Например, при повороте потока на 180 0 (колесо Пельтона) V * 2 • Скоростной напор определяется как

^2— = ^ 2 ^ 2 • ( P 2 ^- P 1 ) ,     (6)

где р и е коэффициенты расхода и расширения соответственно.

Тогда общая сила, действующая на тарель ^Рст + ^Рдин = ^рэф ^{- ( p}2 - ^p1 ^{)- ( 1} + ^vP е² ) . ⁽⁷⁾ включает в свой состав эмпирические коэффициенты V , Р и е , которые зависят от геометрии проточной части клапана [10].

Расчёт статической силовой характеристики с использованием численного анализа картины течения для набора высот подъёма тарели позволяет сократить затраты, связанные с экспериментальным определением эмпирических коэффициентов, входящих в выражение подъёмной силы.

Дискретизация уравнений, описывающих течение рабочей жидкости, проводилась с использованием метода контрольных объёмов. Граничные условия задавались в виде полного и статического давления на входе и выходе соответственно, условие взаимодействия со стенкой, условия симметрии (для уменьшения размерности задачи и экономии вычислительных ресурсов).

Модель течения рабочей жидкости содержит уравнение неразрывности, уравнение сохранения количества движения и модель турбулентности.

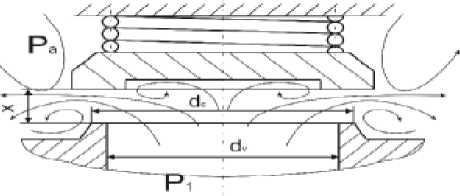
Рис. 4. Расчётная схема взаимодействия

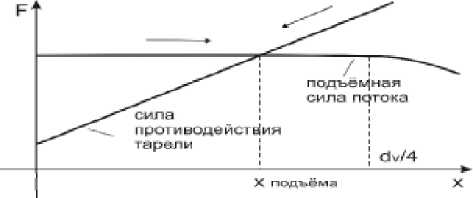
Рис. 5. Идеальная статическая характеристика потока и клапана

потока с тарелью клапана

Уравнение неразрывности, включает в свой состав производную по плотности, так как математическая модель учитывает сжимаемость газа: