Расчёт высокоапертурных конфокальных дифракционно-линзовых объективов

В настоящей работе рассматриваются объективы, предназначенные для копирования микроизображений с заданным увеличением. Наряду с требованиями высокого разрешения (соизмеримого с длиной волны используемого излучения) и ортоскопичности, к таким объективам предъявляется требование телецен-трического хода главных лучей в пространствах предметов и изображений. Телецентричность является одним из необходимых условий достижения одинакового разрешения и равномерной освещённости по всему полю фотоприёмника при условии, конечно, равномерной освещённости предмета, т.е. копируемого носителя микроизображения.

Известно, что рефракционно-линзовые объективы такого типа имеют весьма сложную конструкцию. В частности, фотолитографические объективы, работающие с квазимонохроматическими источниками видимого диапазона, содержат порядка десяти линз [1], а объективы глубокой ультрафиолетовой (DUV – deep ultra-violet) литографии состоят из нескольких десятков линз [2-5]. В то же время, как показано в работах [6-9], объективы, содержащие не более трёх дифракционных линз (ДЛ), уже способны формировать монохроматическое изображение с высоким разрешением по достаточно большому полю. Вышеизложенное обуславливает целесообразность исследования возможностей копирования микроизображений с помощью дифракционно-линзовых объективов.

Параксиальный расчёт

Телецентричность хода главн ых лучей в пространствах предметов и изображений обеспечивается одновременным выполнением двух условий. Во-первых, объектив должен быть конфокальным, т.е. состоять из двух имеющи х положительную оптическую силу частей, и при этом задний фокус передней части должен совпадать с передним фокусом задней части. Во-вторых, общий фокус должен лежать в плоскости апертурной диафрагмы.

При разработке методики параксиального расчёта конфокальных дифракионно-линзовых объективов будем считать заданными габарит системы L, т.е. расстояние от плоскости предмета до плоскости изображения, и линейное увеличение объектива в = У'/У ,

где 2у и 2у' - линейные поля в пространствах предметов и изображений, соответственно.

Используя аппарат матричной гауссовой оптики [10-12] и пренебрегая подложками ДЛ, гауссовы коэффициенты дифракционно-линзового объектива представим в виде

( A B) ( 1 0 Y a

V C D J = V Yj 1 Д q bIf10 J. p Л Y1 1 J

Здесь a  b ।  (1  dj-1 Y1    01  (1  0 Y1

= q  p J    0   1 JI Yj—1 1 J  IY 2 1JV 01

J - число ДЛ объектива, d_j - расстояние между j -ой и ( j + 1 ) -ой линзами, y j - гауссов коэффициент j -ой ДЛ, равный её оптической силе, взятой со знаком минус, т.е. y j =— 1 f j , где f j - фокусное расстояние этой ДЛ [12].

Перемножая первые две матрицы, входящие в уравнение (2), получим

A B || a b || 10

C D J  V a Y j + q  b Y j + p ^J V Y 1 1.

откуда для га уссовы х коэффициентов дифракционно-линзового объектива имеем следующие выражения:

A = a + b Y1,(5)

B = b ,(6)

C = aYj + q + Y1 (bYj + P),

D = byj + p.(8)

Конфокальный объектив афокален, и его гаусcовы коэффициенты имеют следующий вид [10]:

A = P,(9)

C = 0 ,(10)

D = 1 в .(11)

Выражения (5), (7), (9) и (10) позволяют связать гауссовы коэффициенты первой и последней ДЛ с линейным увеличением, толщинами межлинзовых промежутков и гауссовыми коэффициентами остальных ДЛ объектива:

5‘— -в(b-в5).

Подставляя уравнение (16) в соотношение (14) для переднего отрезка объектива, запишем

Yi =

в- a

YJ — -

b q+Y1 p

I ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ a + Y 1 b

J -1

L + в b - Е dj

j —1

1 -в ²

.

.

Передний и задний отрезки объектива связаны с габаритом и суммарной толщиной межлинзовых промежутков соотношением

J -1

^{5 -} 5 — L ^- Е d j ,

j —1

где, в соответствии с принятым в оптике правилом знаков, для действительных предмета и изображения 5 <0, а 5 '>0.

С другой стороны, отрезки 5 ' и 5 связаны между собой через гауссовы коэффициенты [10]

Коррекционные возможности конфокальных объективов-монохроматов

Оценку возможностей коррекции монохроматических аберраций конфокальных дифракционно-линзовых объективов начнём с рассмотренного в работе [8] объектива, состоящего из трёх ДЛ, одна из которых, размещённая в плоскости апертурной диафрагмы, имеет нулевую оптическую силу, т.е. является дифракционной асферикой. Кроме того, что этот объектив является конфокальным, в нём осуществляется пропорциональный (подобный) ход лучей, что обеспечивается расположением предмета и изображения в фокальных плоскостях передней и задней ДЛ, а промежуточное изображение в пространстве между этими

-

/ s

B - A5 D - C5 ’

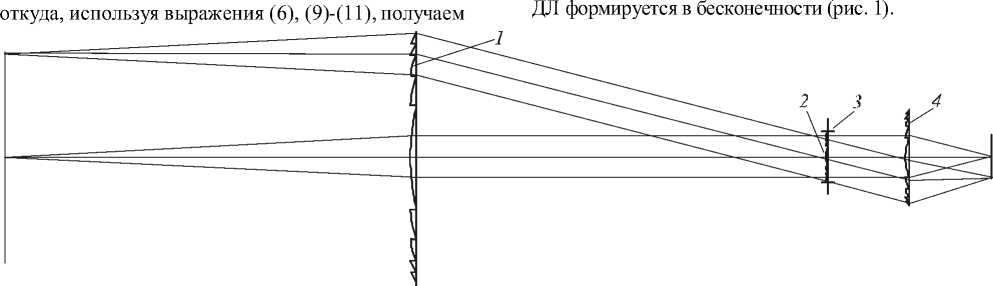
Рис. 1. Оптическая схема пропорционального объектива, состоящего из двух ДЛ (1, 4) и дифракционной асферики (2).3 – апертурная диафрагма

В настоящей работе так же, как и в [13], ДЛ рассматриваются как бесконечно тонкие поверхности, вносящие в луч, падающий на поверхность в точку, отстоящую от оси на расстоянии р , фазовую добавку

v — mЕ Ар2‘.

i —1

При этом фокусное расстояние ДЛ определяется коэффициентом A ₁ :

f ‘—

п

A 1 X m

а коэффициенты A i при i =2,3, .. являются коэффициентами асферических добавок. В формулах (18) и (19) m =1 - рабочий порядок дифракции, % -длина волны излучения.

Отличительной особенностью пропорционального трёхлинзового объектива, оптическая схема которого представлена на рис. 1, является то, что число одновременно устранимых аберраций многократно превышает число коррекционных параметров. В результате он может быть свободным от всех моно- хроматических аберраций третьего и пятого порядков, за исключением второй комы пятого порядка [8]. При этом сферическая аберрация и дисторсия отсутствуют во всех порядках аберрационного разложения. В результате числовая апертура объектива не ограничивается аберрациями и разрешение, по крайней мере, на оптической оси может быть соизмеримо с длиной волной. При этом благодаря отсутствию дисторсии изображение, формируемое объективом, остаётся всегда ортоскопическим.

Так как у рассматриваемого пропорционального дифракционно-линзового объектива в апертурной диафрагме расположена дифракционная асферика, то при параксиальном расчёте её можно не учитывать и считать объектив состоящим из двух ДЛ, разделённых промежутком толщиной d . В этом случае уравнение (3) существенно упрощается:

a b ) (1 d q p J (0 1

а соотношения (12), (13), (16) и (17) принимают вид

В- 1
Y1      , , d	(21)
Y =    Y i	(22)
1 + Y 1 d
L + d ( p- 1) 5 =      1 -в 2    ’	(23)
5 '= —в ( d — в 5 ) .	(24)

Пропорциональный ход лучей обеспечивается при d = L 2, откуда следует, что фокусные расстояния силовых ДЛ рассматриваемого объектива рассчитываются по формулам f'= ^, (25)

f ‘= 2И. ⁽²⁶⁾

Исследования возможностей использования дифракционно-линзовых объективов для целей DUV-литографии производились путём сопоставления их предельно достижимых оптических характеристик с характеристиками рефракционно-линзового фотолитографического объектива ФЕНИКС-248 [14], состоящего из 29 линз и формирующего изображение на длине волны эксимерного KrF-лазера ( % =0,2483 мкм) с пятикратным уменьшением (т.е. при в =—0,2) и с числовой апертурой в пространстве изображений А' =0,65.

При габарите системы L =1440 мм объектив формирует изображение, практически не отличающееся от дифракционно-ограниченного, в пределах поля диаметром 30 мм.

Исследования, выполненные с использованием компьютерной программы оптического проектирования ZEMAX [13], показали, что в результате оптимизации, проводимой по всем конструктивным параметрам дифракционного трёхлинзового объектива, можно практически в отсутствие дисторсии и при вышеуказанных значениях увеличения аперту- ры и габарита получить поле высококачественного монохроматического изображения диаметром порядка 8,5 мм. Здесь и далее оценка качества изображения осуществлялась по критерию Марешаля, согласно которому изображение точечного источника, формируемое оптической системой, практически не отличается от дифракционно-ограниченного, если нормированная интенсивность в дифракционном фокусе, т.е. интенсивность Штреля IS≥0,8 [15].

Поле высококачественного монохроматического изображения, формируемое рассмотренным трёхлинзовым объективом, ограничено в основном нечётными аберрациями высших порядков (и прежде всего комой), вносимыми последней короткофокусной ДЛ. Поэтому исследовалась целесообразность распределения её оптической силы между несколькими ДЛ. В результате была скомпонована пятилинзовая схема, представленная на рис. 2. Коррекция её монохроматических аберраций третьего и пятого порядков, выполнявшаяся с использованием псев-долуче вой методики, изложенной в работах [9, 12], и последующая оптимизация позволили получить конструктивные параметры (см. табл. 1, 2), обеспечивающие поле высококачественного монохроматического изображения диаметром порядка 20 мм. Учитывая, что современные технологии не гарантируют стопроцентной дифракционной эффективности, дальнейшее наращивание числа ДЛ в объективе вряд ли целесообразно.

Следую щим рациональным шагом представлялс я переход к ДЛ, структуры которых разме щены на сферических поверхностях [16]. Эффективность такого шага демонстрируется тем, что уже в случае четырёхлинзового объектива (см. рис. 3 и табл. 3, 4) поле высококачественного монохроматического изображения удалось расширить до 24 мм и при этом дисторсия не превышает %/10 по всему полю. Наибольшую пространственную частоту квазипе-риодической микроструктуры имеет ДЛ, расположенная за апертурной диафрагмой (поз.4 на рис. 3). Минимальный период её микроструктуры соизмерим с длиной волны % .

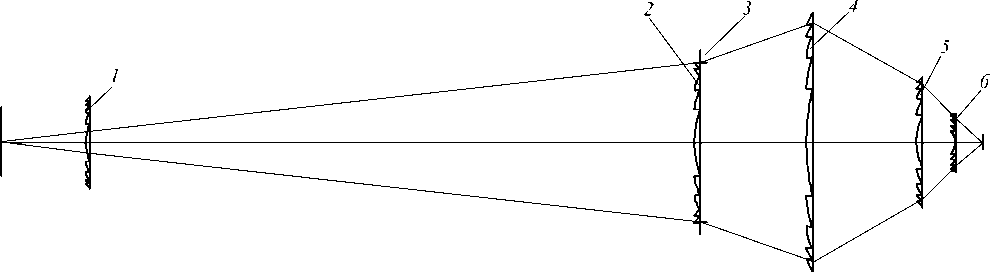
Рис. 2. Оптическая схема конфокального объектива, состоящего из пяти плоских ДЛ (1, 2, 4 – 6). 3 – апертурная диафрагма

Таблица 1. Толщины межлинзовых промежутков в конфокальном объективе, состоящем из пяти плоских ДЛ

Сопряжённые плоскости и № ДЛ	Толщина, мм	Оптическая среда
Плоскость предмета	181,1513	He
1	859,1844	He
2	182,3666	He
3	150,9246	He
4	44,55734	He
5	21,81585	He
Плоскость изображения	0,0000

Таблица 2. Коэффициенты разложения фазовых добавок, вносимых в луч ДЛ конфокального пятилинзового объектива

№ ДЛ A i	1	2	3	4	5
-2 A 1 , мм	-14,726099	-0,26750055	-64,832486	-33,088197	28,874498
A 2 ⋅ 106, мм -4	-2,3598871	526,36699	33,398051	200,03571	2343,525
A 3 ⋅ 1010, мм -6	-114,19023	59,409086	-1,282895	100,4029	27950,339
A 4 ⋅ 1014 , мм -8	1795,7243	9,4719241	1,8835588	-558,34661	-1313763,8
A 5 ⋅ 1018 , мм -10	-13600,013	-1,149598	-1,5066598	1897,6788	27955787
A 6 ⋅ 1022 , мм -12	48047,262	-5,1501782	1,2032907	-4550,5235	-132608220
A 7 ⋅ 1026 , мм -14	-3851,3188	17,888113	-0,61564622	3485,0969	-3806640600
A 8 ⋅ 1030 , мм -16	-635803,31	-23,140408	0,2326898	7755,5394	9900051600
A 9 ⋅ 1034, мм -18	2531281,1	11,979667	-0,081070036	-9677,4279	1631601400000
A 10 ⋅ 1038 , мм -20	-4727234,5	0,7805208	0,0246938	-29250,694	-26889547000000
A 11 ⋅ 1042, мм -22	4469061,5	-3,0751098	-0,0047897975	67778,223	162102180000000
A 12 ⋅ 1046, мм -24	-1720869,6	0,83896487	0,00039879814	-40118,028	-317047140000000

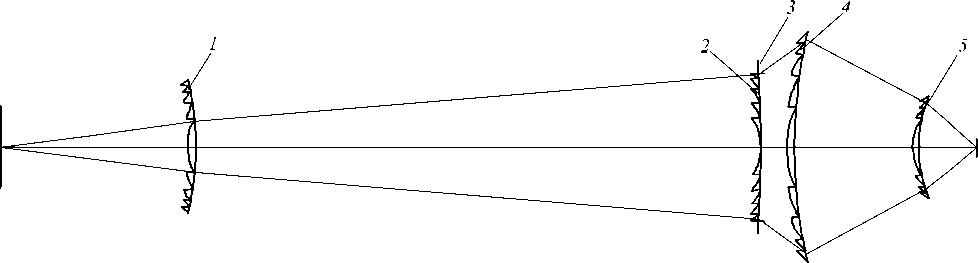
Рис. 3. Оптическая схема конфокального объектива, состоящего из четырёх ДЛ (1, 2, 4, 5), структуры которых размещены на сферических поверхностях. 3 – апертурная диафрагма

Таблица 3. Радиусы поверхностей и толщины межлинзовых промежутков конфокального объектива, состоящего из четырёх ДЛ, структуры которых размещены на сферических поверхностях

Сопряжённые плоскости и № ДЛ	Радиус, мм	Толщина, мм	Оптическая среда
Плоскость предмета	∞	289,0226	He
1	-427,0361	833,8328	He
2	-1257,563	50,09108	He
3	781,1937	183,2285	He
4	177,6755	83,82499	He
Плоскость изображения	∞	0,0000

Таблица 4. Коэффициенты разложения фазовых добавок, вносимых в луч ДЛ конфокального четырёхлинзового объектива

№ ДЛ A i	1	2	3	4
-2 A 1 , мм	-15,173793	47,736909	-87,731316	-51,258192
A 2 ⋅ 106 , мм -4	-13,490748	440,57676	35,738316	219,54919
A 3 ⋅ 1010, мм -6	-28,757868	-31,219811	40,845685	393,57289
A 4 ⋅ 1014 , мм -8	295,07161	-12,122506	-10,129143	-2311,0531
A 5 ⋅ 1018 , мм -10	-1605,2186	43,029778	2,5239472	62574,618
A 6 ⋅ 1022 , мм -12	4688,2233	-43,779299	-1,3572922	-601552,92
A 7 ⋅ 1026, мм -14	-6212,4547	24,848263	0,77014165	3352912
A 8 ⋅ 1030 , мм -16	-2099,9853	-5,1241039	-0,25457438	-11714794
A 9 ⋅ 1034, мм -18	19402,184	0,89951217	0,027196667	26115224
A 10 ⋅ 1038, мм -20	-27602,208	-3,6820576	0,0091677057	-36135891
A 11 ⋅ 1042, мм -22	17461,271	2,9482797	-0,0032651278	28321023
A 12 ⋅ 1046, мм -24	-4301,3834	-0,69528963	0,00030790426	-9616168,4

Учёт ширины полосы излучения лазера

Спектральная ширина линии излучения любого лазера, в том числе и эксимерного, конечна. Поэтому при сопряжении эксимерного лазера с дифракционнолинзовым объективом и оценке качества формируемого изображения необходимо учитывать влияние хроматизма и, прежде всего, продольного, т.е. приращения заднего отрезка, вызываемого отходом длины волны используемого излучения от расчётного значения. В этом случае допустимая спектральная ширина линии может быть оценена по формуле ′

∆λ ≤ ∆smax ,(27)

δs′ где

∆s′max = 1 ΑΑ′2 λ(28)

• -    допустимый хроматизм, определяемый исходя из условия близости качества формируемого изображения к дифракционно-ограниченному [15],

δs′= ds(29)

dλ

• -    относительный продольный хроматизм рассчитанных объективов.

С учётом ранее выбранных значений расчётной длины волны и числовой апертуры в пространстве изображений ( λ =0,2483 мкм и Α′ =0,65) величина ∆s′max ≈ 0,34 мкм. В то же время у рассчитанных дифракционно-линзовых объективов, состоящих из пяти плоских ДЛ или четырёх ДЛ, структуры которых размещены на сферических поверхностях, относительный продольный хроматизм δs′ ≈ 0,9 мкм/пм. Отсюда следует, что эти объективы способны формировать изображение, близкое к дифракционноограниченному при использовании лазерного излу- чения с шириной линии порядка 0,4 пм по уровню 0,5. Это ограничение на ширину спектральной линии сегодня вполне приемлемо.

Действительно, оснащение эксимерных лазеров, специально разработанных для DUV-литографии, дополнительным резонатором с дисперсионными элементами позволяет существенно сузить ширин у спектральной линии [17]. В частности, промышленно выпускаемый KrF-лазер марки К2005 фирмы Lambda Physik USA, Inc. имеет ширину спектральной линии менее 0,4 пм по уровню 0,5, и при этом 95% энергии излучения заключено в спектральном интервале, не превышающем 1,25 пм [18].

Заключение

Проведённые исследования с учётом современных достижений в производстве эксимерных лазеров показывают, что применительно к задачам DUV-литографии дифракционно-линзовые объективы являются вполне конкурентоспособными, т.к. сопоставимые оптические характеристики у них могут быть достигнуты при существенно меньшем количестве линз по сравнению с рефракционнолинзовыми объективами.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009–2013 годы (Госконтракт 16.740.11.0145).