Расчётно-экспериментальное исследование влияния демпфирования конструкции на её долговечность при случайном нагружении

Восьмидесятилетнему юбилею

ЮУрГУ посвящается

На сегодняшний день исследование явления усталости остаётся актуальной задачей, поскольку выход из строя изделий машиностроения чаще всего происходит из-за усталостного разрушения. При этом эксплуатационное воздействие носит случайный характер, в связи с чем оценка долговечности при таком нагружении представляет наибольший интерес. За последние годы количество публикаций, посвящённых этой проблеме, увеличилось в несколько раз. Существует два подхода к оценке долговечности при случайном нагружении [1]. Первым является оценка во временной области, суть которого заключается в анализе всей истории нагружения, схематизации случайного эксплуатационного воздействия и дальнейшей оценке накопленных повреждений. Наибольшее распространение получил метод «падающего дождя», впервые описанный в [2]. Ко второму подходу относятся различные частотные методы. Общей идеей таких методов является использование спектральных характеристик случайного процесса для оценки усталостной долговечности. Основным применением частотных методов является оценка долговечности на стадии проектирования, когда неизвестна история нагружения.

Исследователи не достигли консенсуса в том, какой из подходов к оценке долговечности является наилучшим. В последнее время появляются работы [1, 3, 4], в которых проводится сравнительный обзор существующих методов временной и частотной областей. При этом авторы работ акцентируют внимание на том, что временные подходы оценивают долговечность по напряжениям, деформациям и энергетическим критериям, в том числе в вероятностной постановке. Частотные подходы оценивают долговечность только по напряжениям, не учитывая вероятность разрушения.

Применение частотных методов ограничивается только стационарными процессами, в то время как в реальной эксплуатации преобладают нестационарные воздействия (статистические характеристики процесса изменяются во времени). В связи с этим исследователи разрабатывают новые подходы, учитывающие нестационарность процессов. В работе [5] авторы предлагают метод для анализа нестационарного процесса, скомбинированного из нескольких стационарных. В работах [6, 7] описывается применение плотностей распределения напряжений для оценки долговечности. Также предпринимались попытки совместить временные и частотные подходы [8]. Однако существующие работы рассматривают только определённые типы нестационарных процессов.

Оценка усталостной долговечности характеризуется большими разбросами, поэтому важным аспектом является экспериментальная верификация разработанных методов. Этой проблеме уделено большое количество работ [9–17]. Одной из проблем, вызывающей расхождение расчётных и экспериментальных результатов, является некорректный учёт динамических характеристик изделия: частотная стабильность материала [18] и демпфирующие свойства изделия. В работе [19] на примере ветряного генератора авторы показывают, что долговечность может увеличиться до 67 % при увеличении демпфирования системы. Среди приведенных выше работ только в [11, 15– 17] учитывалось демпфирование при проведении эксперимента.

Целью данной работы является исследование влияния демпфирования на расчётную оценку долговечности при применении разных частотных методов с последующей верификацией экспериментом. В первом разделе даётся информация об использованных в работе методах оценки долговечности. Второй раздел посвящён описанию конечно-элементной модели и численной оценке долговечности. В третьем разделе выполнена экспериментальная верификация расчётных исследований.

Оценка долговечности спектральными методами выполняется на основе статистических характеристик процесса, а именно спектральной плотности мощности (СПМ). СПМ показывает, как энергия распределяется между частотами и является наиболее полным способом описания случайного стационарного процесса. В частотной и временной областях случайный процесс представляется по-разному, связь между этими подходами может быть выражена через спектральные моменты. Спектральные моменты n -го порядка определяются по формуле

A n = J ^ n G( to )d to , 0

где ω – угловая частота в рад/с, G ( ω ) – СПМ сигнала.

Более подробное описание спектральных моментов с точки зрения долговечности приведено в работе [1]. С их помощью можно выразить основные характеристики процесса: частоту пересе- чения среднего уровня (vo) и частоту появления пиков (vp).

_v = 1 A _{v =} _L P l 0   2 ny A0’ p 2 яуА 2

Отношение между двумя этими параметрами называется коэффициентом нерегулярности (γ), который характеризует широкополосность процесса

Y = v ° =   / .2    .

vp Vaa

Для узкополосных процессов коэффициент нерегулярности равен единице, тогда как для широкополосных процессов он стремится к нулю.

В работе долговечность будет оцениваться двумя методами: Narrow band approximation [20], далее в статье называется «метод для узкополосного процесса», и методом Дирлика [21].

Метод для узкополосных процессов базируется на допущении, что в случайных процессах каждый пик соответствует одному циклу. Тогда амплитуды процесса распределены по закону Рэлея и суммарные накопленные повреждения определяются по зависимости [22]:

D nb = V o C ^{- 1} ( V2 A 0 ) k r^ 1 + k ) ,                            (4)

где С и k - постоянные величины кривой усталости материала ( N = ст ^kC ), Г - гамма функция, X 0 – спектральный момент нулевого порядка.

Хорошевский К.А., Ерпалов А.В., Расчётно-экспериментальное исследование Гадолина И.В. влияния демпфирования конструкции на её долговечность...

Метод Дирлика основан на взвешенной сумме распределений Рэлея, Гаусса и экспоненциального. В настоящее время является наиболее распространённым методом оценки в частотной области. Повреждение за время T действия случайной нагрузки рассчитывается по зависимости:

D DK =

= ^ p T ( ^R 0 ) k DQ k Г ( 1 + k ) + ( V2 ) k Г ( 1 + k ) ( D 2 И k + D 3 ) ,

где Z = s/oX - нормированная амплитуда, xm

1/2

,

V ^A 4 7

Q =

₌ ^{2 (} x m   ^Y )

¹ =    1 + 0 2   ,

1,25 ( у — D 3 - D 2 R )

D 1

,

D 2 = ^{1 Y} , D ^{1 +} D" ,   D 3 = 1 — D 1 — D 2 ,

1 — R

R = .Z-xm-DL

1 — Y — D ₁ + D 2 ,

Л 0 , \ , X 2 , Л 3 - спектральные моменты n = 0, 1, 2 и 4 порядков соответственно, a ₂ - параметр ширины спектра.

Численная оценка долговечности конструктивно подобного образца из сплава МА-15 при воздействии случайной вибрации

В качестве объекта исследований выбран конструктивно подобный образец, представляющий собой стандартный плоский образец с галтелью III типа [23], изготовленный их магниевого сплава МА-15, применяемого в авиационной промышленности в конструкциях, требующих повышенного предела текучести при сжатии (модуль упругости E = 4,2×10⁴ МПа, коэффициент Пуассона µ = 0,035, плотность ρ = 1 850 кг/м³), с грузом массой 47,6 г, установленным на свободной стороне образца для снижения собственной частоты колебаний. Эскиз образца с размерами приведён на рис. 1, а .

Кривая усталости задана зависимостью N = s ^6,7 х 10^18,95, где $ - это уровень напряжений.

Динамические испытания проводились при консольном изгибе. Для реализации такого нагружения образец с одной стороны жестко крепился к вибростолу, с другой стороны образец был свободно вывешен вместе с грузом (рис. 1, б ).

Плоскость закрепления

Ø8

Место крепления груза

Груз

Образец

б)

а)

Рис. 1. Эскиз образца с размерами (а) и установленные образцы на испытательном стенде (б)

Первый этап исследования – это построение конечно-элементной модели образца с последующим проведением численного модального анализа и определением напряжений, развиваемых на поверхности образца при случайном нагружении. Структурная схема численного расчёта долговечности представлена на рис. 2.

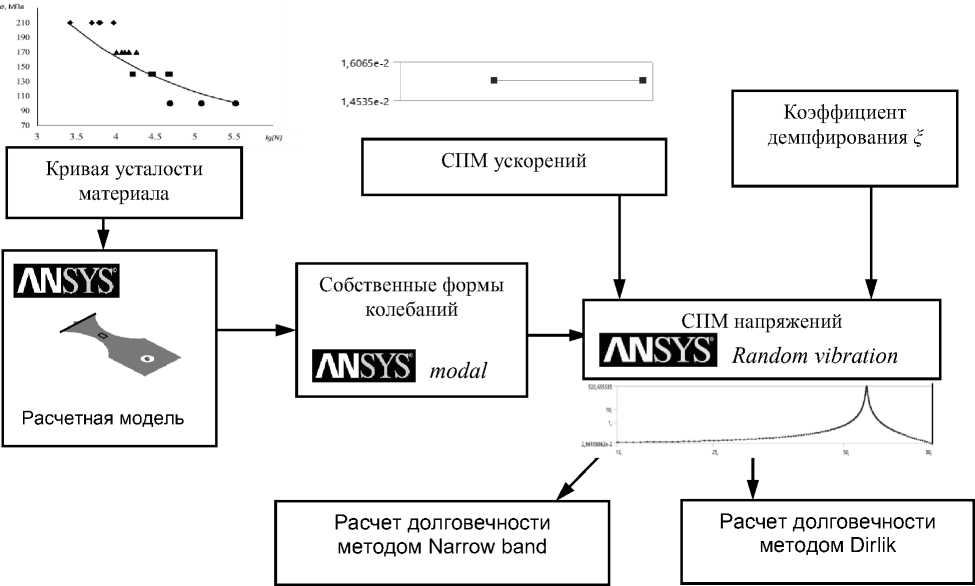
Рис. 2. Структурная схема расчёта долговечности при случайном нагружении

Конечно-элементная сетка и численный модальный анализ реализованы в программном пакете ANSYS. Использовались оболочечные элементы, размер элемента 0,5 мм, в модели 6 270 узлов и 6 051 элемент.

По результатам модального анализа первая изгибная собственная форма колебаний идентифицирована на частоте 57 Гц. С целью проявления этой формы колебания и принимая во внимание ограничения оборудования, выбран частотный диапазон случайной вибрации от 15 до 80 Гц.

Для оценки долговечности спектральными методами необходимо знать спектральную плотность напряжений, развиваемых в наиболее нагруженной точке образца. Она построена с помощью модуля ANSYS Random Vibration. Входным воздействием является случайная вибрация с постоянным уровнем дисперсии виброускорений («белый» шум»), направленная вдоль вертикальной оси стенда (см. рис. 1). Случайная вибрация задана спектральной плотностью виброускорений, характерный вид которой показан на рис. 3.

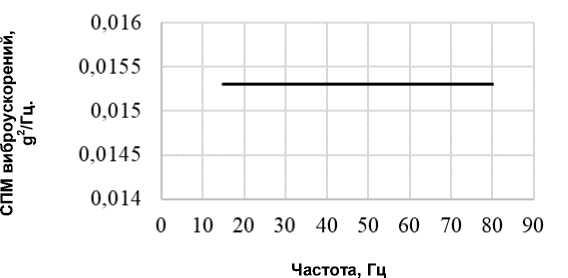
Рис. 3. Спектральная плотность виброускорений для уровня 0,0153 g2/Гц

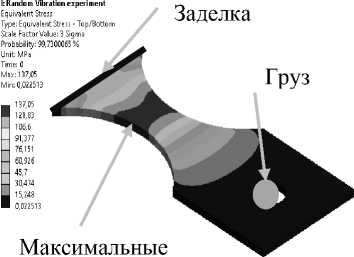
Исследовались три расчётных случая с дисперсией на уровнях: 0,01245 g²/Гц, 0,0153 g²/Гц и 0,018 g²/Гц. Картина распределения эквивалентных напряжений для 0,018 g²/Гц в образце показана на рис. 4, а . Для остальных случаев картина похожа.

напряжения

а )

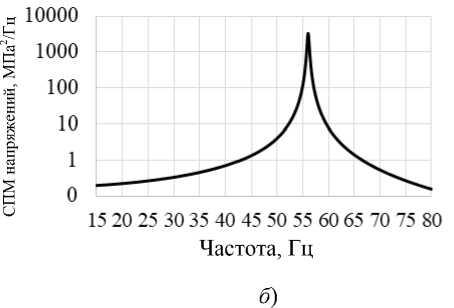
Рис. 4. Распределение эквивалентных напряжений с вероятностью 99 % в образце при случайных колебаниях (расчётный случай – 0,018 g²/Гц) ( а ). Спектральная плотность напряжений в наиболее нагруженной точке ( б )

Для наиболее нагруженной точки образца средствами программного комплекса ANSYS рассчитана спектральная плотность напряжений. Характерный вид спектральной плотности напряжений показан на рис. 4, б (ось ординат в логарифмическом масштабе).

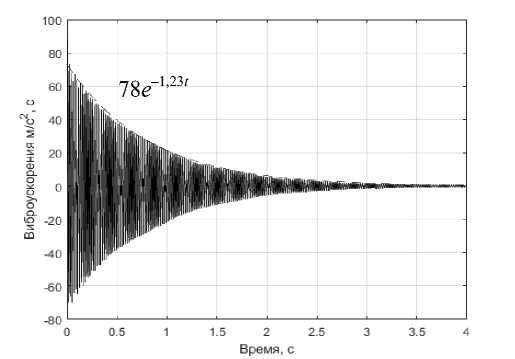
Одной из основных динамических характеристик конструкции является коэффициент демпфирования, который характеризует способность конструкции поглощать энергию колебаний. При вибрационном воздействии перемещения конструкции зависят от величины коэффициента демпфирования. При его низких значениях перемещения будут большими, что, в свою очередь, вызовет высокие напряжения в конструкции [15]. Особенно важным это свойство является при резонансе, когда амплитуды перемещений увеличиваются в несколько раз. Коэффициент демпфирования определяется только экспериментальным путём. Поэтому для уточнения конечноэлементной модели проведено экспериментальное исследование демпфирующих свойств конструктивно подобного образца. Определение коэффициента демпфирования осуществлялось по затухающим колебаниям согласно методике, описанной в [24]. Образец обладает малой массой, поэтому для исключения искажения динамических характеристик, вызванных установкой дополнительных датчиков, применялся бесконтактный способ регистрации вибрации с помощью лазерного виброметра компании Polytec. Виброметр устанавливался таким образом, чтобы лазерный луч располагался перпендикулярно образцу (рис. 6, б ). Затухающие колебания возбуждались с помощью модального молотка. Экспериментальная установка и характерная виброграмма затухающих колебаний показана на рис. 6, a .

Для анализа вводится допущение, что рассматриваемая система обладает линейным вязким демпфированием. Тогда через максимумы виброграммы затухающих колебаний можно провести огибающую, которая описывается экспоненциальным законом Ae^–nt .

В таком случае логарифмический декремент колебаний рассчитывается по зависимости δ = n τ ,                                         (6)

где n – коэффициент затухания, τ – период колебаний.

Относительный коэффициент демпфирования оценивается по зависимости:

δ

. 2 π

Выполнив серию из десяти экспериментов, выявили диапазон изменения коэффициента демпфирования: от 0,0024 до 0,0035. Для дальнейшей оценки долговечности выбран весь диапа- зон его изменения.

а )                                                             б )

Рис. 6. Характерная виброграмма затухающих колебаний ( а ) и лазерный виброметр с образцами в оснастке ( б )

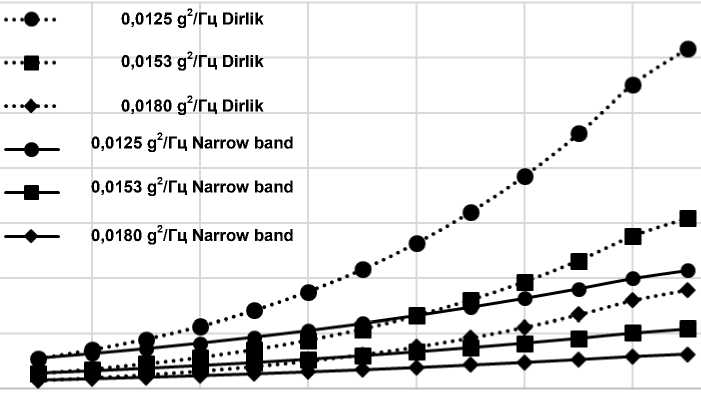
Долговечность частотными методами определяется с помощью спектральной плотности напряжений в наиболее нагруженной точке. Оценка выполнялась двумя методами: методом для узкополосного процесса и методом Дирлика. Результаты расчетов с учетом вариативности демпфирования показаны на рис. 7.

0.0023    0.0025    0.0027    0.0029    0.0031    0.0033    0.0035    0.0037

Коэффициент демпфирования

Рис. 7. Долговечности образцов в зависимости от коэффициента демпфирования

Сравнивая полученные значения, видим, что метод Дирлика даёт бóльший допускаемый диапазон долговечностей, чем метод для узкополосного процесса. При малых значениях коэффициента демпфирования долговечности, определенные методами Дирлика и для узкополосного случайного процесса, показывают близкие значения, разница не превышает 2 %. С увеличением демпфирования разница увеличивается до 64 %.

Экспериментальная верификация

Заключительным этапом исследования является экспериментальная верификация проведенных расчетов. Испытания проведены при консольном изгибе образцов с заданием случайного воздействия. Образцы испытывались до разрушения, общий вид испытательной установки с образцами показан на рис. 8, а . Реализовано три случая нагружения: 0,018, 0,153 и 0,0125 g²/Гц. На уровне 0,018 g²/Гц испытывалось шесть образцов, на уровне 0,0153 g²/Гц – две группы по шесть образцов, на уровне 0,0125 g²/Гц – четыре образца.

Логарифм времени до разрушения

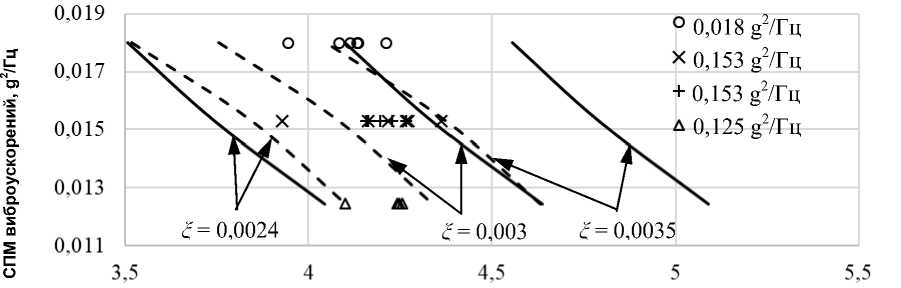
Рис. 8. Расчётные и экспериментальные результаты: пунктирная линия – долговечность по методу для узкополосного процесса, сплошная линия – долговечность по методу Дирлика, маркеры – экспериментальные данные

Сравнение экспериментальных результатов с расчётными зависимостями представлено на рис. 8, б . Видно, что экспериментальные данные находятся практически полностью в пределах диапазона, ограниченного кривыми, полученными методом для узкополосного процесса, и полностью входят в диапазон, ограниченный кривыми, полученными методом Дирлика. Анализируя полученные результаты, важно отметить сильное влияние коэффициента демпфирования на расчетную долговечность объектов исследования. В таблице приведена погрешность экспериментальных данных в сравнении с кривыми, полученными численными методами, для значений коэффициента демпфирования ξ = 0,003. В данном случае коэффициент демпфирования выбирался как среднее значение исследуемого диапазона его изменения.

Разница между экспериментальными и численными результатами ( ξ = 0,003)

Номер образца	Погрешность, %
	Метод для узкополосного процесса			Метод Дирлика
	0,0125 g2/Гц	0,0153 g2/Гц	0,0180 g2/Гц	0,0125 g2/Гц	0,0153 g2/Гц	0,0180 g2/Гц
1	–35	–13	20	–145	–103	–43
2	–88	17	46	–243	–49	3
3	–32	22	42	–140	–40	–4
4	–32	32	48	–140	–23	7
5	–	35	49	–	–17	8
6	–	36	57	–	–16	23
Среднее	–47	21	44	–167	–41	–1

Из таблицы видно, что на низком уровне (0,0125 g2/Гц) СПМ-виброускорений численные методы дают завышенную оценку долговечности: метод для узкополосного процесса завышает оценку в среднем на 47 %, метод Дирлика – в среднем на 167 %. При увеличении СПМ-виброускорений метод для узкополосного процесса занижает оценку долговечности (21 % для СПМ 0,0153 g2/Гц и 44 % для СПМ 0,0180 g2/Гц). Метод Дирлика даёт завышенную оценку (41 % для СПМ 0,0153 g2/Гц и 1% для СПМ 0,0180 g2/Гц).

Исследовано влияние демпфирования на долговечность при расчёте частотными методами. Разработана конечно-элементная модель исследуемого объекта для получения спектральной плотности напряжений в наиболее нагруженной точке. Экспериментально выявлен диапазон изменения коэффициента демпфирования объекта исследования. Выполнены численные расчёты на долговечность с учётом коэффициента демпфирования методами для узкополосного процесса и методом Дирлика.

Установлено, что метод Дирлика более чувствителен к изменению демпфирования конструкции. При этом для низкого уровня нагружения разница рассчитанной долговечности в сравнении с полученной экспериментально достигает 167 %, с увеличением уровня нагрузок разница снижается до 1 %. Для узкополосного процесса разница рассчитанной долговечности в сравнении с полученной экспериментально для всех уровней нагружения в среднем варьируется в пределах 50 %. Таким образом, величина коэффициента демпфирования может существенно влиять на расчётную долговечность, изменяя её в разы.

Исследование выполнено за счет гранта Российского научного фонда № 23-29-10097,

• 1.    A Comparative Review of Time- and Frequency-Domain Methods for Fatigue Damage Assessment / M. Muñiz-Calvente, A. Álvarez-Vázquez, F. Pelayo et al. // Int. J. Fatigue. – 2022. – Vol. 163. – P. 107069.

• 2.    Rain Flow Method / T. Endo, M. Matsuishi, K. Mitsunaga et al. // Kyushu Institute of Technology Academic Repository. – 1974. – Vol. 28. – P. 33–62.

• 3.    Gadolina, I.V. Varied Approaches to Loading Assessment in Fatigue Studies / I.V. Gadolina, N.A. Makhutov, A.V. Erpalov // Int. J. Fatigue. – 2021. – Vol. 144. – P. 106035.

• 4.    Zorman, A. Vibration Fatigue by Spectral Methods – A Review with Open-Source Support / A. Zorman, J. Slavič, M. Boltežar // Mechanical Systems and Signal Processing. – 2023. – Vol. 190. – P. 110149.

• 5.    Benasciutti, D. Frequency-Based Fatigue Analysis of Non-Stationary Switching Random Loads / D. Benasciutti, R. Tovo // Fatigue Fract. Eng. Mater. Struct. – 2007. – Vol. 30, no. 11. – P. 1016–1029.

• 6.    Braccesi, C. Random Fatigue. A New Frequency Domain Criterion for the Damage Evaluation of Mechanical Components / C. Braccesi, F. Cianetti, L. Tomassini // Int. J. Fatigue. – 2015. – Vol. 70. – P. 417–427.

• 7.    Park, J.B. A New Fatigue Prediction Model for Marine Structures Subject to Wide band Stress Process / J.B. Park, J. Choung, K.S. Kim // Ocean Eng. – 2014. – Vol. 76. – P. 144–151.

• 8.    Evaluation of Mechanical Component Fatigue Behavior under Random Loads: Indirect Frequency Domain Method / C. Braccesi, F. Cianetti, G. Lori, D. Pioli // Int. J. Fatigue. – 2014. – Vol. 61. – P. 141–150.

• 9.    Marques, J.M.E. Fatigue Analysis of Nonstationary Random Loadings Measured in an Industrial Vehicle Wheel: Uncertainty of Fatigue Damage / J.M.E. Marques, L. Solazzi, D. Benasciutti // Metals. – 2022. – Vol. 12, no. 4. – P. 616.

• 10.    Akbaba, Ö.M. Vibration Based Fatigue Analysis of a Structure Integrated on an Air Vehicle by Using Experimental and Theoretical Methods / Ö.M. Akbaba, B. Yildirım, G. Canbaloğlu // Results Eng. – 2022. – Vol. 15. – P. 100549.

• 11.    Demirel, G.I. Implementation of Dirlik’s Damage Model for the Vibration Fatigue Analysis / G.I. Demirel, A. Kayran // Procedia Struct. Integr. – 2019. – Vol. 21. – P. 101–111.

• 12.    Wang, Y. Adapted Locati Method used for Accelerated Fatigue Test under Random Vibrations / Y. Wang, R. Serra, E.P. Argoul // Procedia Struct. Integr. – 2019. – Vol. 19. – P. 674–681.

• 13    Fatigue Life Extimation of a Military Aircraft Structure subjected to Random Loads / G. Zucca, F. Cianetti, M. Palmieri et al. // Procedia Struct. Integr. – 2018. – Vol. 12. – P. 183–195.

• 14.    Non-Gaussianity and Non-Stationarity in Vibration Fatigue / M. Palmieri, M. Česnik, J. Slavič et al. // Int. J. Fatigue. – 2017. – Vol. 97. – P. 9–19.

• 15.    Kihm, F. Influence of the Modal Damping on the Estimated Fatigue Life / F. Kihm, A. Langelier, K. Munson // Procedia Eng. – 2018. – Vol. 213. – P. 270–281.

• 16.    Fatigue Reliability Analysis System for Key Components of Aero-Engine / H. Qi, Y. Lu, S. Song, Q. Xu // International Journal of Aerospace Engineering. – 2022. – Vol. 2022. – Article ID: 1143901.

• 17.    Zorman, A. Short-Time Fatigue-Life Estimation for Non-Stationary Processes Considering Structural Dynamics / A. Zorman, J. Slavič, M. Boltežar // International Journal of Fatigue. – 2021. – Vol. 147. – P. 106178.

• 18.    Мыльников, В.В. Метод изучения частотной стабильности материалов при испытаниях на многоцикловую усталость стали / В.В. Мыльников, Э.А. Дмитриев // Известия высших учебных заведений. Черная Металлургия. – 2023. – Т. 66, № 3. – С. 367–375.

• 19.    Rezaei, R. Fatigue Life Sensitivity of Monopile-Supported Offshore Wind Turbines to Damping / R. Rezaei, P. Fromme, P. Duffour // Renewable Energy. – 2018. – Vol. 123. – P. 450–459.

• 20.    Miles, J.W. On Structural Fatigue under Random Loading / J.W. Miles // J. Aeronaut. Sci. – 1954. – Vol. 21, no. 11. – P. 753–762.

• 21.    Dirlik, T. Application of Computers in Fatigue Analysis: PhD thesis / T. Dirlik. – University of Warwick., UK, 1985. – 234 p.

• 22.    Mršnik, M. Frequency-Domain Methods for a Vibration-Fatigue-Life Estimation – Application to Real Data / M. Mršnik, J. Slavič, M. Boltežar // International Journal of Fatigue. – 2013. – Vol. 47. – P. 8–17.

• 23.    ГОСТ 25.502-79. Методы механических испытаний металлов. Метод испытаний на усталость. – М: Изд-во стандартов, 1979. – 44 с.

• 24.    Нашиф, А. Демпфирование колебаний / А. Нашиф, Д. Джоунс, Д. Хендерсон. – М.: Мир, 1988. – 448 p.

Поступила в редакцию 28 сентября 2023 г.

Bulletin of the South Ural State University Series “Mathematics. Mechanics. Physics” 2023, vol. 15, no. 4, pp. 47–57

A COMPUTATIONAL AND EXPERIMENTAL STUDY INTO THE INFLUENCE OF STRUCTURAL DAMPING ON A STRUCTURE’S DURABILITY UNDER RANDOM LOADING

K.A. Khoroshevskii ¹ , A.V. Erpalov ¹ , I.V. Gadolina ²

• ¹    South Ural State University, Chelyabinsk, Russian Federation

• ²    Mechanical Engineering Research Institute of the Russian Academy of Sciences, Moscow, Russian Federation

Received September 28, 2023

Erpalov Aleksey Viktorovich is Cand. Sc. (Engineering), Senior Staff Scientist, South Ural State University, Chelyabinsk, Russian Federation.

Gadolina Irina Victorovna is Cand. Sc. (Engineering), Senior Staff Scientist, Mechanical Engineering Research Institute of the Russian Academy of Sciences, Moscow, Russian Federation.