Распознавание моторных образов на электроэнцефалограммах с применением свёрточных нейронных сетей

Электроэнцефалография является одним из популярных на сегодняшний день неинвазивных методов исследования активности головного мозга. Сигналы электроэнцефалограммы (ЭЭГ) отражают совокупную электрическую активность нейронов в коре головного мозга. Изучая эти данные, можно получить много полезной информации о состоянии человека. Такие сигналы содержат богатую семантическую информацию, которая может быть соотнесена с когнитивными, зрительными или моторными функциями человека.

Одним из примеров таких сигналов могут служить моторные образы, определяемые как воображение двигательного действия без какой-либо эфферентной информации для нервно-мышечной системы. Исследования показали, что, когда человек представляет движение конечностей, определённые частотные компоненты ЭЭГ, такие как мю и центральные бета-ритмы, (де) синхронизируются в контралатеральной сенсомоторной области [1]. В случаях поздней стадии бокового амиотрофического склероза, тяжёлых нервно-мышечных расстройств и парализаций, вызванных травмами спинного мозга, люди не способны производить произвольные движения мышц. Однако сенсорные и когнитивные функции мозга лишь минимально затронуты такими заболеваниями. С помощью интерфейса мозг–компьютер (ИМК), на основе сигналов ЭЭГ, человек получает возможность взаимодействовать с окружающим миром. Сигналы ЭЭГ во время представления моторных образов могут использоваться в качестве управляющих сигналов для приложений ИМК (управление курсором, выбор букв или слов, управление протезом, навигация в инвалидной коляске). Использование таких систем ве- дёт к улучшению качества жизни больных. Исследование закономерностей формирования электрофизиологической активации сенсомоторной коры головного мозга человека при мысленной активации моторных образов является актуальной и востребованной задачей для построения таких систем.

Изучение ЭЭГ связано со множеством трудностей, таких как зависимость сигналов от возраста пациента, времени суток. Большое влияние оказывают на сигнал присутствие шумов, помех и слабая степень структурированности.

Для исследования ЭЭГ могут быть использованы методы классической математики, основанные на частотно-временном, волновом или компонентном анализе. Однако их применение зачастую не даёт устойчивых результатов распознавания различных состояний человека, а в некоторых случаях их применение становится крайне затруднительным из-за сложности алгоритмов [2–5]. Сигналы головного мозга отличаются большой сложностью, что и является основной причиной данной проблемы. Классические математические приёмы (преобразования Фурье, вейвлетный анализ и т.д.) основаны на выделении полезного сигнала из всего массива данных и дальнейшей алгоритмической работы с ним. Выделение отдельных сигналов в фиксированных частотных полосах ЭЭГ обеспечивает грубое понимание психического состояния человека. Для сигналов, регистрируемых в сложных условиях психофизиологических экспериментов, зачастую выделение такого полезного сигнала оказывается затруднительным, а при малейшем изменении состояния методика может перестать работать.

Использование искусственных нейронных сетей (ИНС) в прикладных областях, таких как интерфейс мозг–компьютер, является на сегодняшний день перспективным направлением [6–10]. Способность ИНС к адаптивному обучению, устойчивость к искажению сигнала и хорошему обобщающему эффекту делает их отличным инструментом классификации [11–13].

Существует несколько подходов к классификации временных рядов с использованием ИНС [14]. Ключевым фактором успеха распознавания видов человеческой деятельности на основе анализа ЭЭГ является эффективное использование данных, полученных с измерительных датчиков. В данной работе используются методы, предложенные в [15–17]. В этих методах временной ряд преобразуется в изображения, после чего применяется свёрточная нейронная сеть для их анализа.

Данная работа посвящена созданию систем для распознавания моторных образов (движение правой и левой руки) на основе сигналов ЭЭГ. Процессы, связанные с моторными образами, крайне сложны, изменения частотно-временной структуры электроэнцефалограмм не систематичны и варьируются для каждого человека. Изменение сигнала ЭЭГ может быть использовано для распознавания моторных образов.

Преобразование на основе матрицы Грама

Первый используемый метод обозначается как преобразование на основе матрицы Грама ( Gramian Angular Field , GAF) [16, 17]. В этом методе временной ряд преобразуется в полярную систему координат. На основе полученных данных строится матрица G , каждый элемент которой равен косинусу суммы углов. Полученная матрица преобразуется в изображение, которое подаётся на вход свёрточной нейронной сети.

При таком преобразовании обеспечивается сохранение временной зависимости. Основная диагональ – это частный случай при k =0, содержит исходные значения и угловую информацию.

Матрица G – это матрица, построенная по ряду X = ( x 1 , x 2 , ..., x n ) следующим образом:

• 1.    Сначала ряд нормируется в отрезок [-1, 1]:

• 2.    Далее полученные значения переводятся в полярную систему координат, кодируя амплитудные значения в виде углового косинуса и соответствующие временные значения в качестве радиуса:

• 3.    Сама матрица G вычисляется по формуле:

„ _ ( x i - max( X )) + ( x i - min( X )) x i =      max( X ) - min( X )

.

ф i = arccos( xi), ti ri   N , где ti – значение времени в точке i, N – полный временной интервал.

cos( Ф 1 +Ф 1) — cos( Ф 1 +Ф n ) cos( ф ₂ +ф 1 ) — cos( ф ₂ +ф _n )

cos( ф n +Ф 1 ) — cos( ф n +ф n )

Итоговая матрица сохраняет всю информацию о ряде, кроме исходных границ значений x i , которые мы теряем в шаге (1) после процедуры нормализации [17] . Таким образом, мы можем по полученной матрице восстановить исходный ряд, но только отмасштабиро-ванный в отрезок [-1, 1].

На основе полученных матриц формируются изображения для дальнейшего использования. Так как цветовые каналы в рассматриваемом случае не несут в себе полезной информации, в работе используются полутоновые изображения ( grayscale ), что позволило уменьшить количество каналов изображений в 3 раза в сравнение с RGB - вариантом. На рис. 1 приведён пример представления сигнала ЭЭГ после преобразования на основе матрицы Грама.

Преобразование на основе Марковской матрицы перехода

Ещё одним методом преобразования исходного временного ряда в изображения является метод Мар- ковской матрицы перехода (Markov Transition Field, MTF) [17]. В отличие от преобразования на основе матрицы Грама, исходные границы ряда и распределение значений ряда, которые теряются при применении операций свёртки и пулинга к матрице G, сохраняются в Марковской матрице. На первом этапе происходит квантование исходного временного ряда с использованием метода аппроксимации (Symbolic Aggregate approXimation, SAX) [18]. Затем вычисляется матрица переходов Маркова (квантованный временной ряд рассматривается как цепь Маркова) и, наконец, вычисляется поле перехода Маркова из матрицы переходов.

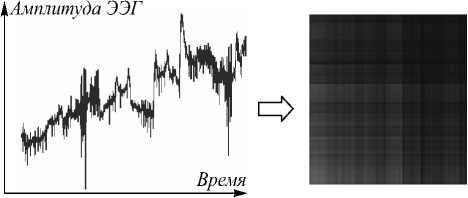
Рис. 1. Графическое представление сигнала ЭЭГ после преобразования на основе матрицы Грама

Процесс квантования исходного временного ряда заключается в разбиении множества значений наблюдений на m интервалов (отрезков с одинаковой вероятностью попадания значения наблюдения в каждый из них). Это можно просто сделать с помощью обучающей выборки, объединив все значения наблюдений переменной в одно множество, отсортировать его, а дальше так расставить в нём Q - 1 границ, чтобы между двумя соседними границами было примерно одинаковое количество значений. Пространство между двумя соседними границами и будет q i интервалом.

На основе полученных интервалов строится матрица размером Q×Q путём подсчёта переходов между интервалами в виде цепочки Маркова первого порядка вдоль оси времени. Далее матрица нормализуется по формуле

Q

• Z p >, = 1.

j = 1

Данная матрица является стохастической, то есть строки или столбцы в сумме дают единицу. В такой матрице каждая строка будет иметь собственное распределение вероятностей

P 11 •" P1Q P 21 •" P 2 Q

PQ 1 - PQQ

Марковская матрица отбрасывает условную связь между распределением X и зависимостью от временных шагов ti. Однако избавление от временной зависимости приводит к слишком большой потере информации в матрице W. Марковское поле перехода (МПП) расширяет Марковскую матрицу, выравнивая каждую вероятность по временной оси. Интервалами, содержащими данные в моменты времени ti и tj, являются qi и qj (q e [1, Q]). Mij в МПП обозначает вероятность перехода qi → qj. То есть мы разложим матрицу W, которая содержит вероятность перехода по оси амплитуды в матрицу МПП, с учётом временных позиций. МПП определяется следующим образом:

M =

^M 11

^M 21

^M 1 Q

^M 2 Q

MQ 1 ^- MQQ

Таким образом, происходит преобразование матрицы Маркова первого порядка, которая содержит вероятности перехода из одного состояния в другое, в матрицу МПП, учитывающую значения времени. Полное математическое описание преобразования представлено в [17]. На рис. 2 приведён пример преобразования сигнала ЭЭГ на основе Марковского поля перехода.

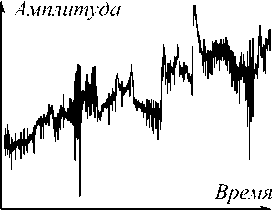
Рис. 2. Графическое представление сигнала ЭЭГ после преобразования на основе Марковской матрицы перехода

Архитектура глубокой свёрточной нейронной сети

В данной работе была разработана архитектура глубокой СНС, адаптированная для классификации ЭЭГ-сигнала, с учётом количества измерительных электродов. Входные изображения подаются на вход сети в виде 64- канального изображения, где каждый канал является трансформированным сигналом электроэнцефалограммы. Архитектура глубокой СНС состоит из основных слоёв: трёх свёрточных и трёх полносвязных. Сеть содержит 128 нейронов на первом слое свёртки, 256 на втором и 512 на третьем, далее следуют полносвязные слои, содержащие 512, 256, 128, 64 и 3 нейрона соответственно. Параметры сети определялись методом подбора.

Используемые данные

Для исследования были выбраны данные, представленные в [19]. Каждый испытуемый находился на кресле с подлокотниками и наблюдал за изображением на мониторе. В начале каждого испытания на мониторе в течение двух секунд отображался чёрный экран с крестом, далее испытуемому в течение трёх секунд необходимо было представлять движение руки в зависимости от указаний на мониторе. После этого следовал короткий перерыв в течение нескольких секунд, по завершении которого действие повторялось.

Набор данных представляет собой сигналы ЭЭГ, записанные с применением системы BCI 2000 [20] и использованием 64 электродов при частоте дискретизации 512 Гц. Частотные фильтры для преобразова- ния данных не использовались.

Порядок эксперимента, а также преобразование исходных данных в изображения на основе матрицы Грама представлены на рис. 3. Для обучения нейронных сетей использовались данные первых десяти ис- пытуемых.

Рис. 3. Порядок эксперимента и его иллюстрация в изображениях

Структура модели

Так как в исследуемых электроэнцефалограммах представлены сигналы, полученные с 64 электродов, то в качестве входных параметров модели получается такое же количество изображений. Изображения преобразуются по аналогии с RGB - изображением во входной вектор, однако если в случае с RGB -изображением используется 3 канала, по одному на каждый цвет, то в данном случае на вход подается 64- канальное изображение, содержащее преобразованный ЭЭГ сигнал. На выходе нейронной сети оценивается принадлежность преобразованных в изображения сигналов ЭЭГ к одному из трёх классов мысленной активности испытуемого: воображаемое движение правой или левой рукой и состояние покоя. Структурная схема итоговой нейросетевой модели представлена на рис. 4.

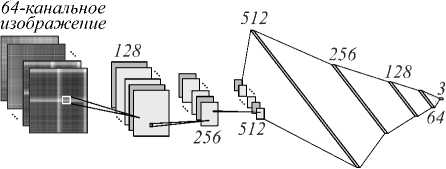
Рис. 4. Структурная схема итоговой модели свёрточной нейронной сети для классификации моторных образов

Влияние разрешения входных изображений на точность классификации

Для исследования влияния разрешения входных изображений на результаты распознавания моторных образов были использованы данные первого испытуемого. Под распознаванием моторных образов понимается классификация соответствующих интервалов ЭЭГ, во время которых испытуемый представлял движения правой или левой рукой, а также состояние покоя. Под точностью классификации понимается соотношение верно классифицированных интервалов ЭЭГ к полному количеству исследованных интервалов. Результаты распознавания моторных образов для четырёх разрешений представлены в табл. 1.

Табл. 1. Сравнение влияния разрешения изображений преобразованного ЭЭГ сигнала на основе матрицы Грама на точность классификации

Разрешение	Количество параметров сети	Точность
32×32	5638403	0,792
64×64	20392195	0,875
128×128	49899779	0,97
256×256	108914947	0,98

Из полученных результатов можно сделать вывод, что изображения с разрешением 128×128 оптимально подходят для дальнейших исследований, т.к. точность при их использовании незначительно отличается от изображений с разрешением 256×256, однако количество параметров сети в первом случае вдвое меньше, что повышает быстродействие сети и уменьшает время, требуемое на её обучение.

Сравнение полученных результатов

В табл. 2 приведены результаты сравнения полученных результатов с данными по классификации моторных образов, представленными в [19].

Табл. 2. Сравнение точности классификации моторных образов

№ испытуемого	GAF	MTF	Источник
1	0,97	0,93	0,8
2	0,87	0,97	0,47
3	0,89	0,99	0,91
4	0,92	0,92	0,88
5	0,87	0,99	0,71
6	0,95	0,96	0,81
7	0,81	0,92	0,49
8	0,98	0,99	0,47
9	0,83	0,98	0,69
10	0,91	0,94	0,75
Средняя точность	0,9	0,96	0,7

Среднее значение точности распознавания моторных образов с использованием преобразования на основе матрицы Грама составила порядка 90 %, с использованием преобразования на основе Марковской матрицы перехода – 96 %. Для всех рассмотренных случаев предложенные методы показывают лучшие результаты классификации по сравнению с приведенными в оригинальном источнике (70%) [14]. При этом преобразование на основе Марковской матрицы перехода для всех испытуемых показывает точность распознаваний выше 90%.

Заключение

В статье была изучена возможность применения методов преобразования ЭЭГ сигнала на основе мат- рицы Грама и Марковской матрицы перехода для обнаружения моторных образов. В результате проведённых экспериментов установлено, что без применения дополнительной фильтрации может быть получена высокая точность распознавания моторных образов. Наилучшая точность в исследуемой выборке составляет порядка 99 %. Общие результаты свидетельствуют, что данный метод даёт более высокую точность, чем методы, описанные в источнике данных. Проведённые исследования показали возможность использования комбинации преобразований сигналов ЭЭГ в сочетании со свёрточными нейронными сетями для распознавания моторных образов. Использование такого метода делает затруднительным анализ особенностей сигнала после всех преобразований, однако в задачах классификации, где в первую очередь важна точность распознавания, данный метод показывает высокие результаты. Оценка влияния разрешения на результаты классификации моторных образов позволяет выбрать разрешения входных изображения, обеспечивающих оптимальное соотношение точности и параметров нейронной сети. Представленный метод классификации электроэнцефалограмм может быть использован для построения интерфейса мозг - компьютер.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта No 18-08-00977 А и было поддержано Программой повышения конкурентоспособности Томского политехнического университета.